行星架是行星传动中结构比较复杂而重要的构件。当行星架作为基本构件时，它是机构中承受外力矩最大的零件。因此，行星架的结构设计和制造质量，对各行星轮间的载荷分配以及传动装置的承载能力、噪声和振动等有重大影响。

（1）行星架的结构设计

行星架的常见结构形式有双臂整体式（图8-65和图8-66）、双臂装配式（图8-67）

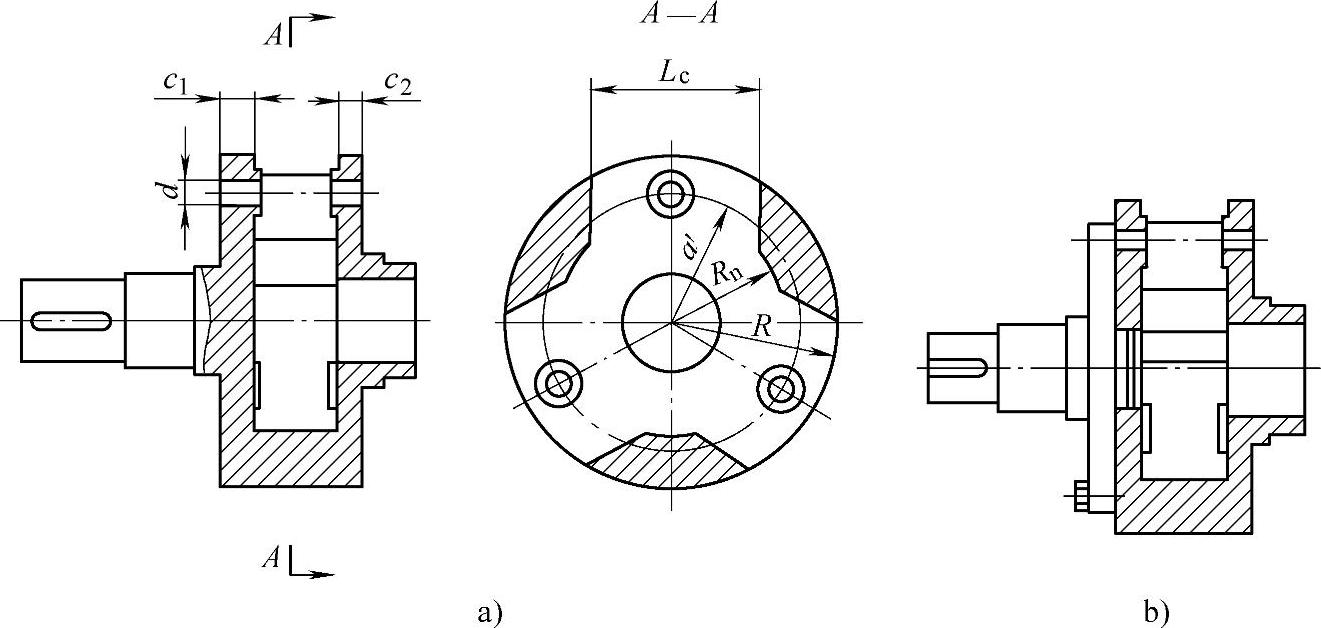
图8-65 双臂整体式行星架

a）轴与行星架一体结构 b）轴与行星架法兰连接

和单臂式（图8-68）三种。在制造工艺上又有铸造式、锻造式和焊接式（图8-69）等。

双臂式整体行星架结构刚性比较好，采用铸造和焊接方法，可得到与成品尺寸相近的毛坯，加工量小。铸造行星架的结构如图8-65和图8-66所示。铸造行星架常用于批量生产的中、小型行星减速器中，这种情况下如用锻造，则加工量大，浪费材料和工时，不经济。

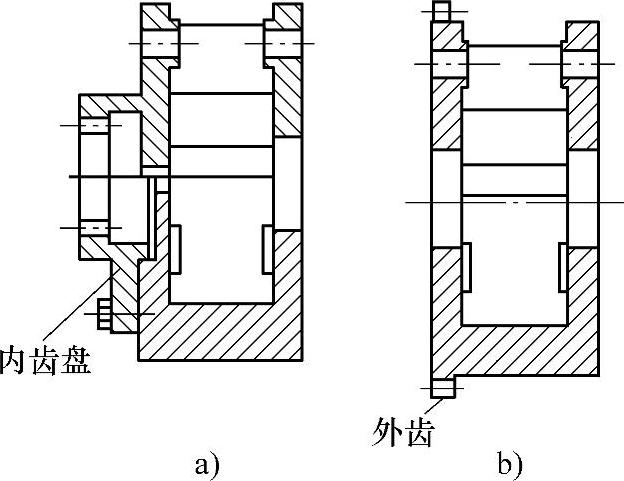
图8-66 双臂整体式带齿的浮动行星架结构

a）内齿式 b）外齿式

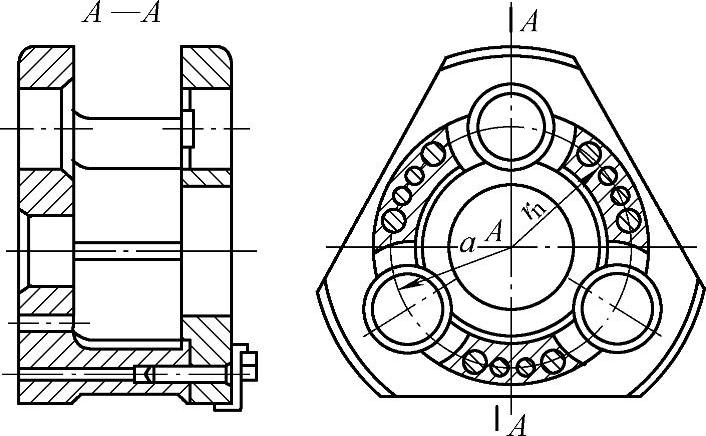
图8-67 双臂装配式行星架

焊接行星架通常用于单件生产的大型行星传动结构中，其结构如图8-69所示。

针对低速级行星架与出轴采用焊接连接结构时难以保证焊缝质量的难题，行星架与出轴采用由一组精制螺栓或空心销连接并传递转矩，用螺栓锁紧的装配式结构，不仅工艺简单而且连接可靠，如图8-65b所示。

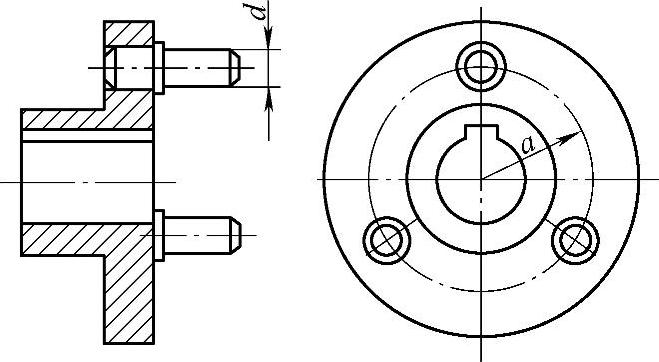
图8-68 单臂式行星架

双臂式整体行星架常用于传动比较大（如NGW型单级iⁱ_aH＞4）、行星轮轴承装在行星轮内的设计场合。

双臂装配式行星架主要用于传动比较小的情况（NGW型i^b_aH≤4）及高速行星传动的某些设计中。

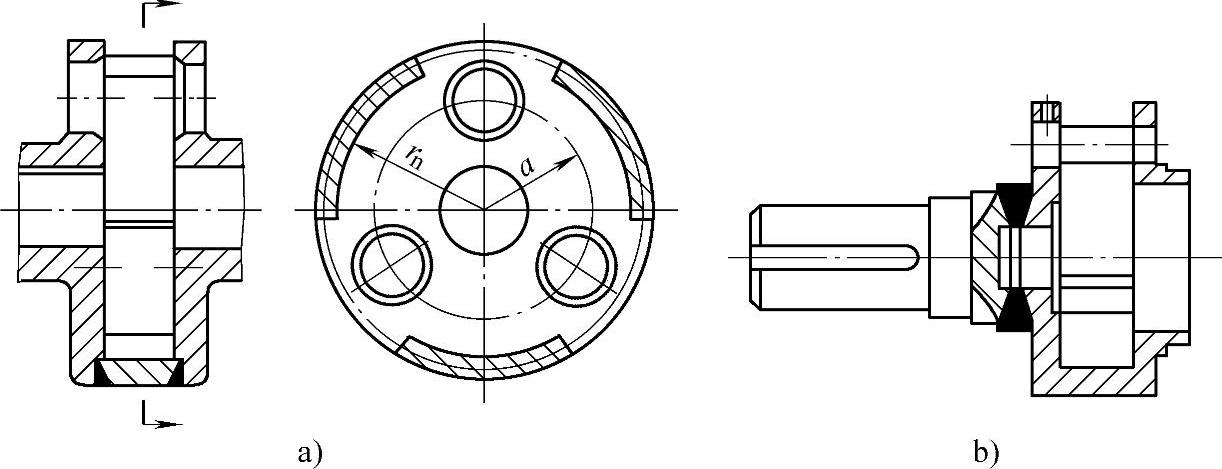
图8-69 焊接式行星架

双臂整体式和双臂装配式行星架的两个臂（或称侧板），通过中间的连接板（梁）连接在一起，两侧板的壁厚，当不装轴承时可按经验公式选择：c₁≈（0.25～0.3）a′，c₂≈（0.2～0.25）a′。尺寸L_c应比行星轮外径大10mm以上。连接板内圆半径R_n按比值R_n/R≤0.85～0.5确定，如图8-65a所示。

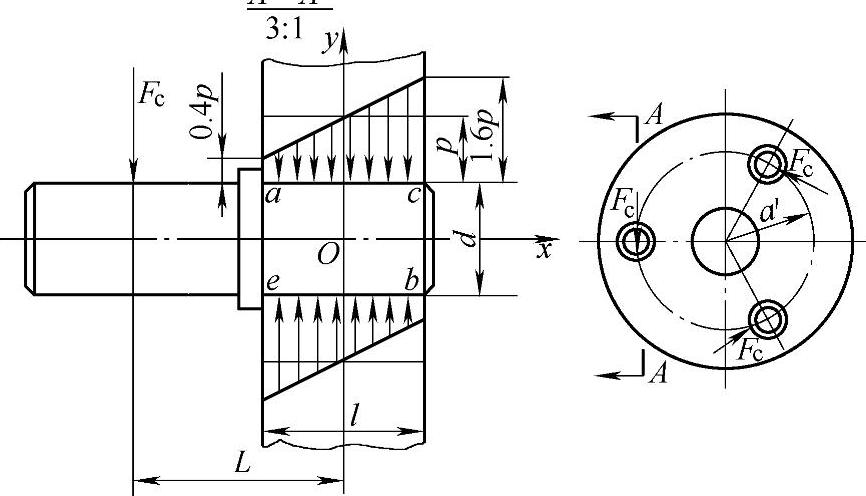
图8-70 单臂式行星架心轴与孔的过盈配合计算简图

单臂式行星架结构简单，但行星轮轴呈悬臂状态，受力情况不好。对于图8-68所示结构，轴径d要按抗弯强度和刚度计算。轴和孔采用过盈配合推荐用

,用温差法装配。配合长度（即行星架厚度）可在（1.5～2.5）d范围内选取。其过盈配合连接的强度可按下列公式计算。

如图8-70所示，根据平衡条件，取a、b两点剩余压力为0.4p时，需由配合产生的压应为（MPa）近似为

对于NGW型传动，F_c为齿轮圆周力F_t的2倍，则

根据p值即可求出配合过盈量，选择配合种类，并可用压力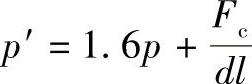，验算e点的塑性变形和挤压强度。

图8-71所示是另一单臂式行星架结构，与图8-68比较，改变了行星轮心轴的受力状态，即由心轴2受压应力变为螺栓3受拉应力，再由螺栓3受拉变为心轴2和行星架1通过止口连接，呈端面受压状态。为防止高速运转下，行星轮受离心力影响，在心轴2的开口端用空心圆盘4将各心轴连接起来，并用端盖5将空心圆盘4紧固在心轴2上，使离心力相互抵消，以减少心轴2所受的附加弯矩。这类结构的另一优点是心轴定位止口的尺寸短，均布在同一平面上，便于保证安装和加工精度。其缺点是零件数目多。

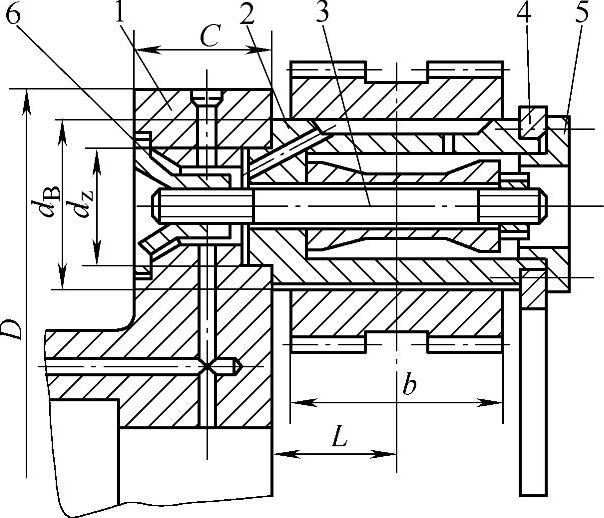
图8-71 单臂式行星架

1—行星架 2—心轴 3—螺栓 4—空心圆盘 5—端盖 6—螺母

心轴止口处的连接强度进行验算的原则是保证心轴受载后，止口处承压的半圆面不离缝，承压增大时半圆面不产生塑性变形。如图8-72所示止口承压面的压力由p₀和p_F两部分组成，合成后的压力，B点为p_max，A点为p_min。

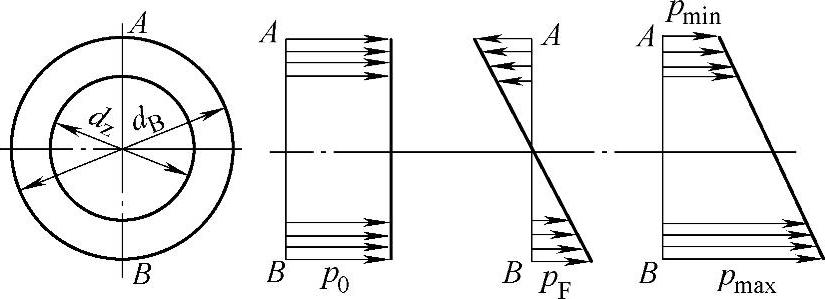
图8-72 心轴止口处压力分布

p₀为螺栓拧紧时产生的压力，计算公式为

式中 F₀——螺栓的拉力；

S——环形承压面积，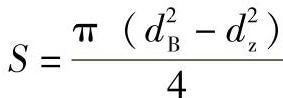

d_B——心轴外径，取行星轮齿根圆的65%～70%；

d_z——止口直径，取d_z=0.8d_B。

p_F为行星轮作用于心轴上的力F_c产生的力矩所引起的压力计算公式为

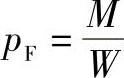
式中 M——F_c产生的力矩，M=F_cL，L为齿宽中心至止口承压面的距离；

W——环面的抗弯截面模量，。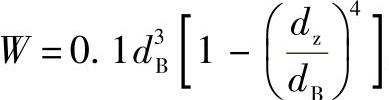

A点的合成压力为

p_min=p₀-p_F

B点的合成压力为

p_max=p₀+p_F

为了连接可靠，应保证：

p_min≥（0.3～0.4）p₀

p_max≤[p]=（0.3～0.4）σ_s

式中，σ_s为材料屈服点。

当然，除此之外，图8-71中的螺母6、螺栓3也要按一般资料进行强度验算，行星架主要结构的外形尺寸可按经验公式确定：

行星架厚度C≈0.5b，b为齿轮宽度；

行星架外径D≈2a′+0.8d_c，a′为中心距，d_c为行星轮分度圆直径。

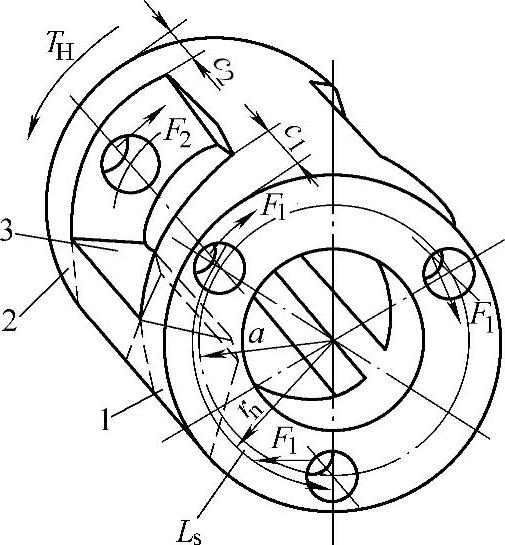
图8-73 行星架计算模型

1、2—侧板 3—连接板

（2）行星架的变形计算

行星架结构比较复杂，通常将其模拟为由侧板及中间等距离的连接板组成的框架结构进行变形计算，如图8-73所示。

行星架的变形指在转矩作用下，侧板1相对于侧板2的位移，位移值Δ在半径r_n圆周的切线方向度量。半径为r_n的圆通过连接板3的断面形心O_n（图8-74）。对于梯形断面，r_n按下式计算：

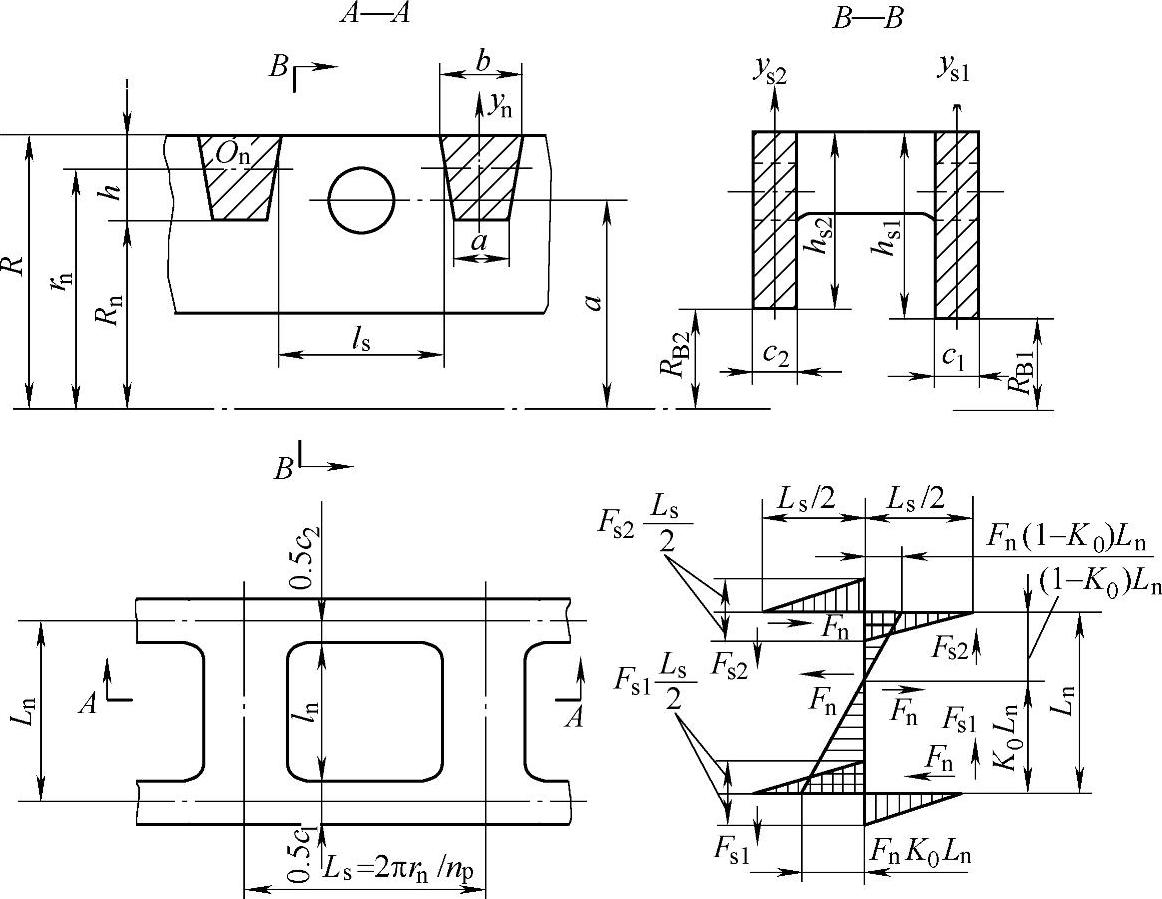
图8-74 行星架沿半径r_n展开图

式中 R——行星架外圆半径；

a、b、h_n——梯形断面尺寸。

位移量Δ由下式表示的作用力引起：

(www.daowen.com)

式中 F₁——行星轮心轴作用于行星架侧板1上的切向力，径向力对行星架不产生转矩，可不计入。

位移量Δ通过将连接板看成双支点梁，计算其在F_n力作用下产生的挠度来确定。连接板两端与侧板固接处的弯矩为

M_s1=F_s1L_s

M_s2=F_s2Ls

力F_s1和F_s2可根据行星架的平衡条件（图8-73）求得：

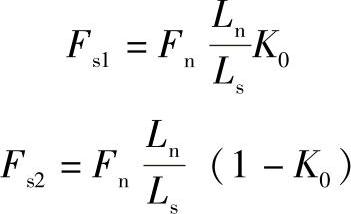
式中 L_s——沿半径为r_n的圆周上侧板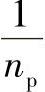段弧长，即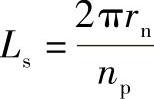

L_n——连接板长度，等于两侧板中心平面间的距离，即L_n=L_n+0.5c₁+0.5c₂；

K₀——两侧板的刚度比较系数，K₀决定连接板弯矩为零的点的位置。

Δ值与力F_n的比值为行星架的柔度，由式（8-129）确定：

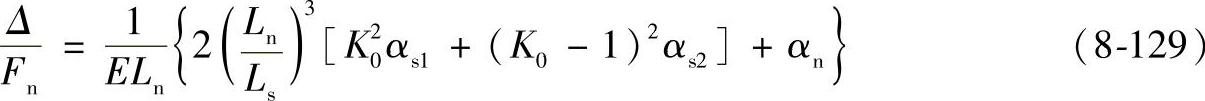
式中 E——材料弹性模量；

α_s、σ_n——^F_n力对侧板与连接板的弯曲变形和剪切变形的影响系数。

侧板和连接板的影响系数和刚度比较系数可按下式计算：

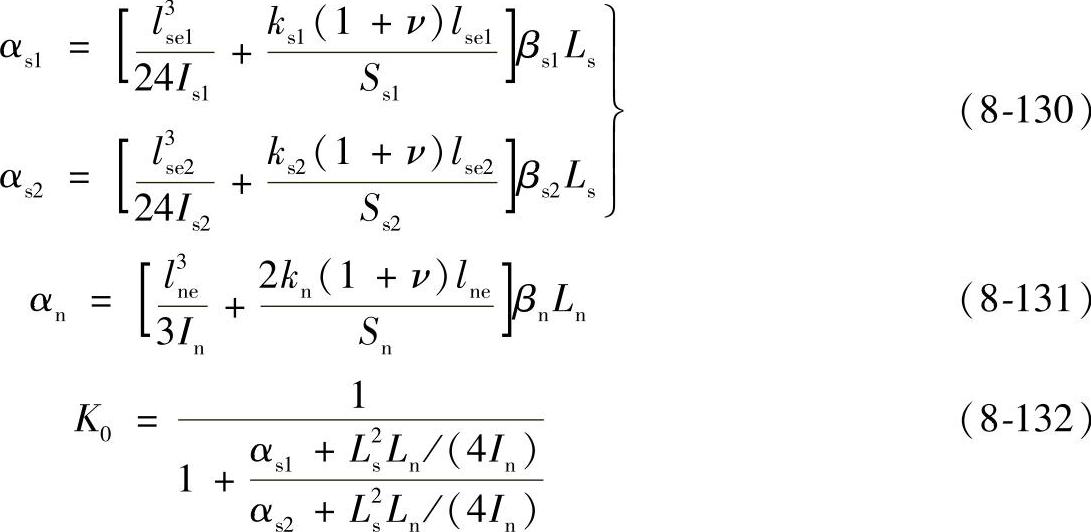
式中 β_s——圆盘形侧板的形状系数；

β_n——凸四边形连接板的形状系数；

k_s、k_n——侧板和连接板的横截面形状系数；

I_s、I_n——侧板（相对于y_s轴）和连接板（相对于y_n轴）横截面的惯性矩；

l_se、lne——相当于悬臂梁变形的侧板和连接板元件的有效长度；

ν——泊松比（对于钢，ν=0.3）。对于矩形截面的侧板：

I_s1=h_s1C³₁/12；I_s2=h_s2C³₂/12

S_s1=h_s1C₁；S_a2=h_s2C2；k_s=1.2对于横截面近似于梯形的连接板：

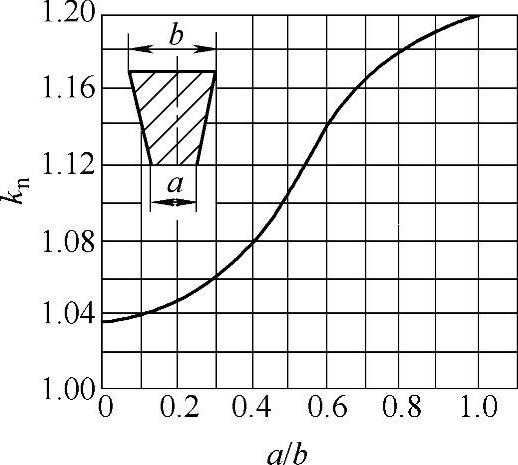
图8-75 确定系数k_n的曲线图

系数k_n可由图8-75确定。对于连接板近似于等腰三角形时（a=0），应取k_n=1.03。

如果连接板本身就是行星轮的心轴d，则I_n=πd⁴/64；S_n=πd²/4；k=1.11；如果行星轮心轴压装在矩形截面的侧板上，则l_se、l_ne的值可由图8-76确定。

对于侧板，可看成是圆盘形（带中心孔、带中心孔且外圈有凸缘或带轴颈）的结构方案，系数β_s按下式计算：

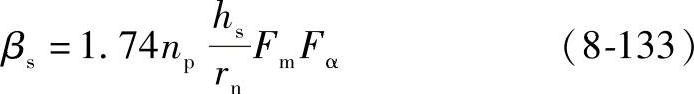
式中，F_m、F_α根据参数m=R_n/R，n=R_b/R及n_p、α（连接板断面两侧在半径r_n的圆周上中心角为2α），由图8-77确定。

当连接板是直径为d的悬臂行星轮心轴时：

R_n=r_n-0.5d；α≈d/2rn

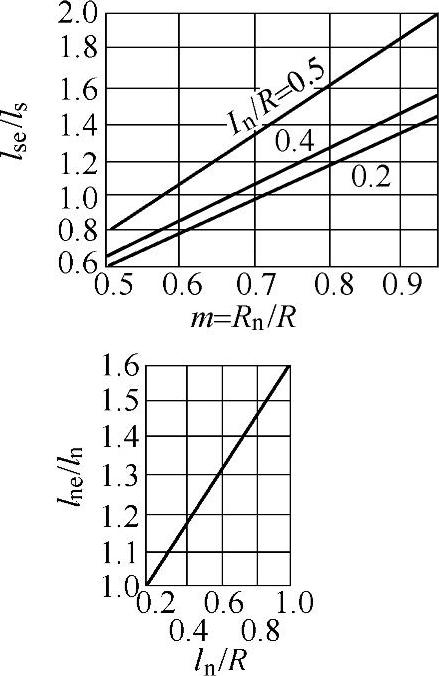
图8-76 确定L_se和L_ne的关系图

对于广泛采用的连接板尺寸比例，其形状系数可取β_n=1。当R_n/R＞0.9和d/l_s＞0.5时，系数β_n和β_s必须用试验的方法精确确定。

对于不同结构的行星架，上述计算柔度的公式可针对具体情况给以简化。

1）当行星架两侧板等刚度（图8-77a），α_s1=α_s2=α_s，K₀=0.5时

α_s和α_n按式（8-130）、式（8-131）计算。

2）当行星架的一个侧板刚性夹紧（图8-78b），如与机体固定，α_s2→0，α_s1=a_s时

Δ

而、α_s和α_n值按式（8-129）、式（8-130）、式（8-131）计算。F

3）当行星架的两个侧板被刚性夹紧（图8-78c），α_s1=α_s2→0，K₀=0.5时

α_n按式（8-131）计算。

4）当行星轮心轴悬臂式地固定在单臂式行星架上（图8-78d），α_s1=α_s，α_s2→∝，K₀=1时

5）当力矩作用在行星架连接板中间，且两侧板等刚度（图8-78e），α_s1=α_s2=αs△F

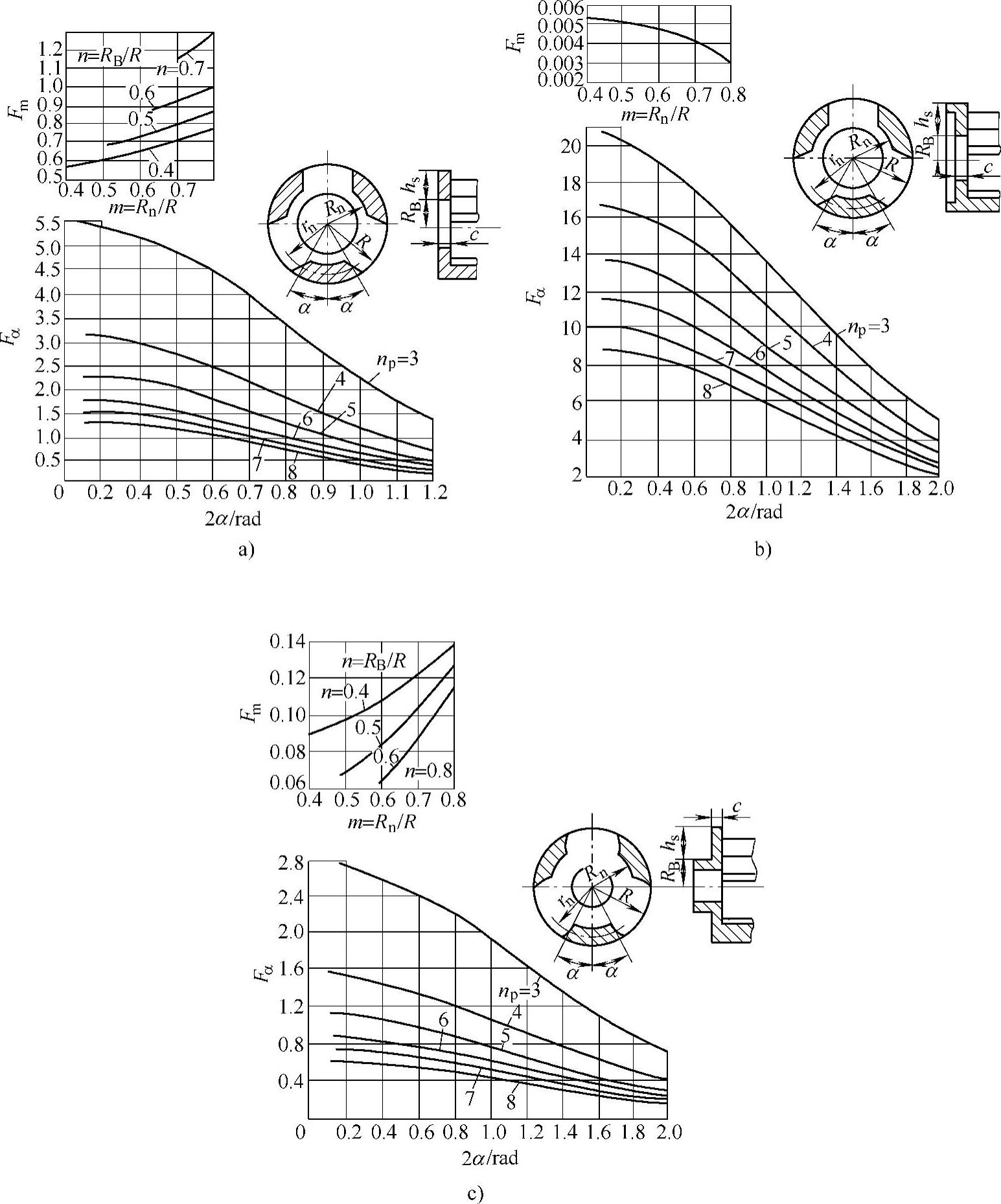
图8-77 确定F_m、F_α的曲线图

a）有中心孔的行星架侧板b）外圈有凸缘的行星架侧板c）与传动轴连接的行星架侧板时

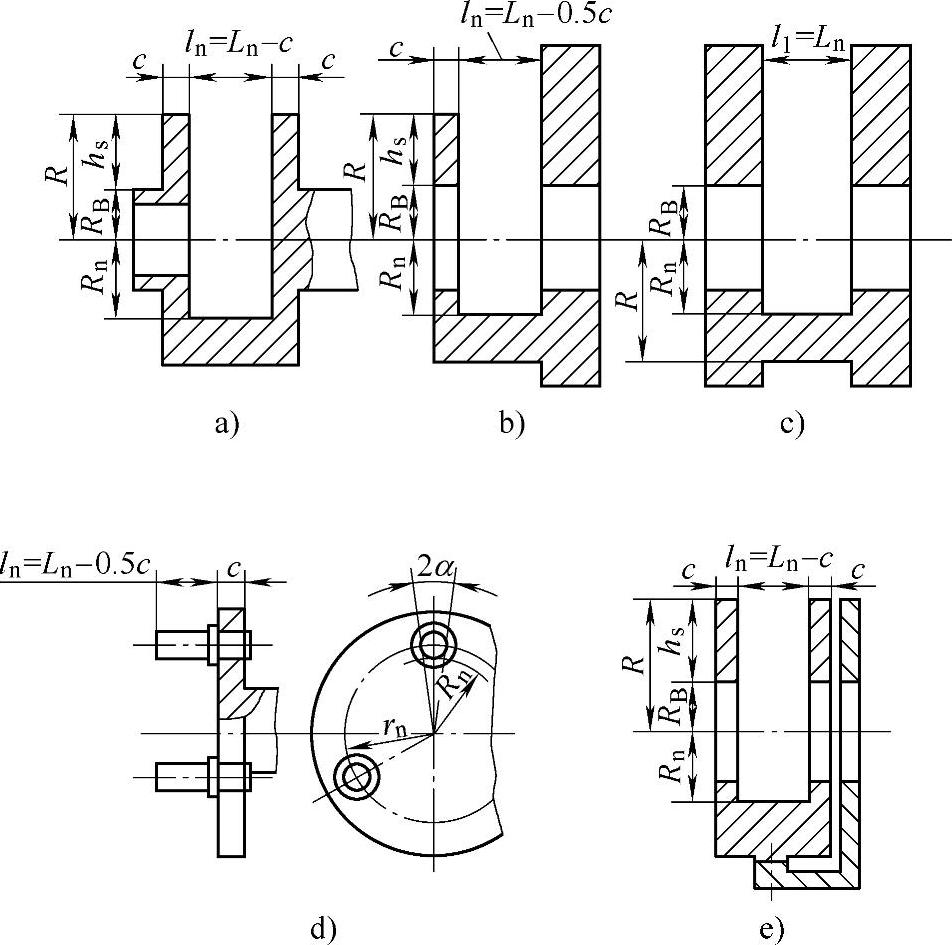
图8-78 行星架结构计算简图

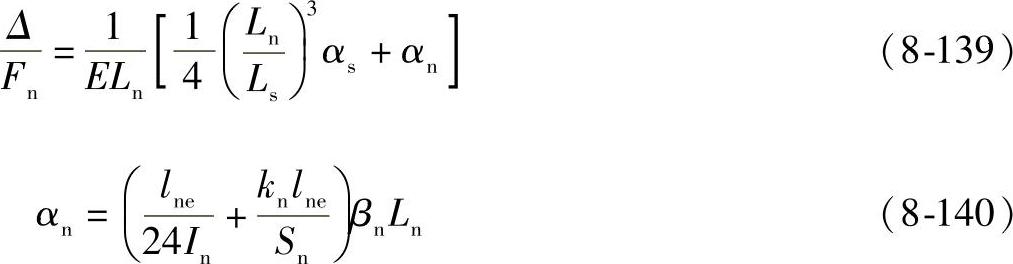
α_s按公式（8-130）确定。

行星架柔度的许用极限值，可通过因行星架变形，而引起的行星轮轮齿相对于太阳轮轮齿的歪斜角γ来评定：

式中，L_n值根据图8-78中不同结构图的相应值代入。a′和α′为中心距和啮合角。

对于单臂式行星架，行星轮心轴长为l_n，其歪斜角为

当力矩对称作用于连接板时（图8-78e），行星架变形不会使行星轮轮齿发生歪斜，即γ=0°。

行星架目前大多采用球墨铸铁件和焊接结构，可以简化结构，减少加工工作量，特别是大型、带输出轴的行星架，大多采用焊接结构。焊接结构可以减轻行星架的重量，但焊后及粗加工后应作消除应力处理，焊条采用E5015。焊接结构行星架的典型结构如图8-79～图8-81所示。

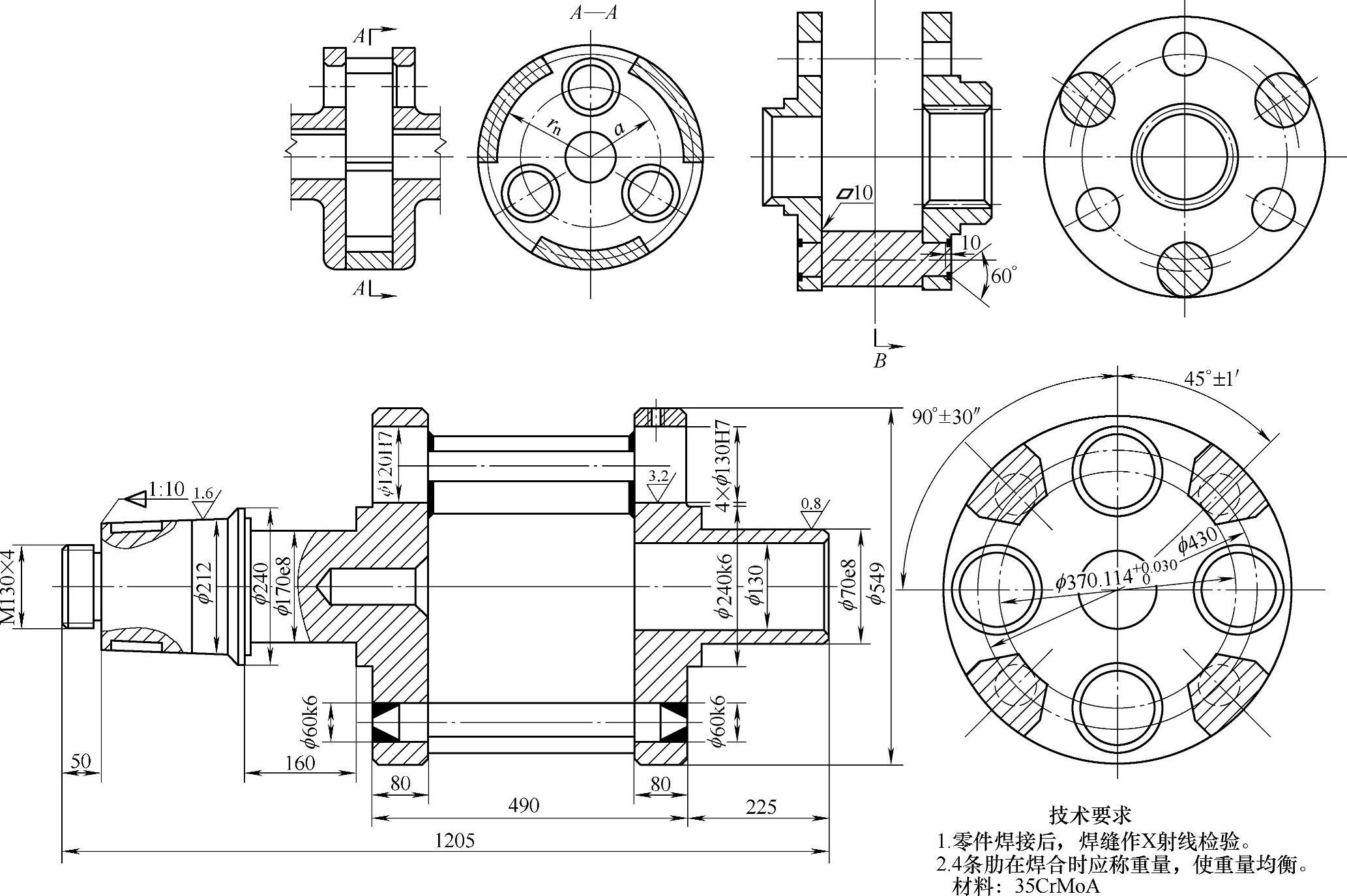
图8-79 焊接结构的行星架（一）

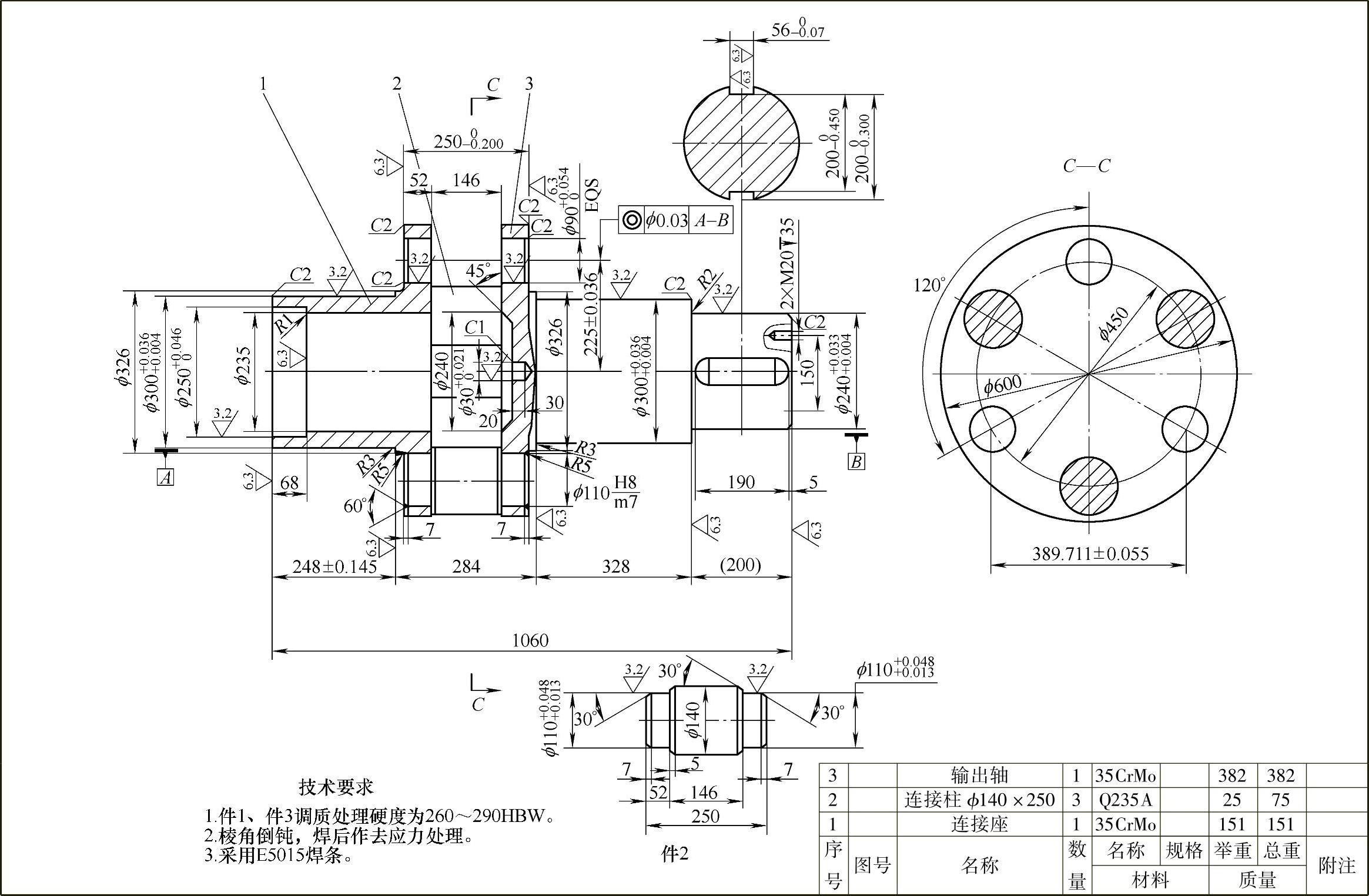
图8-80 焊接结构的行星架（二）

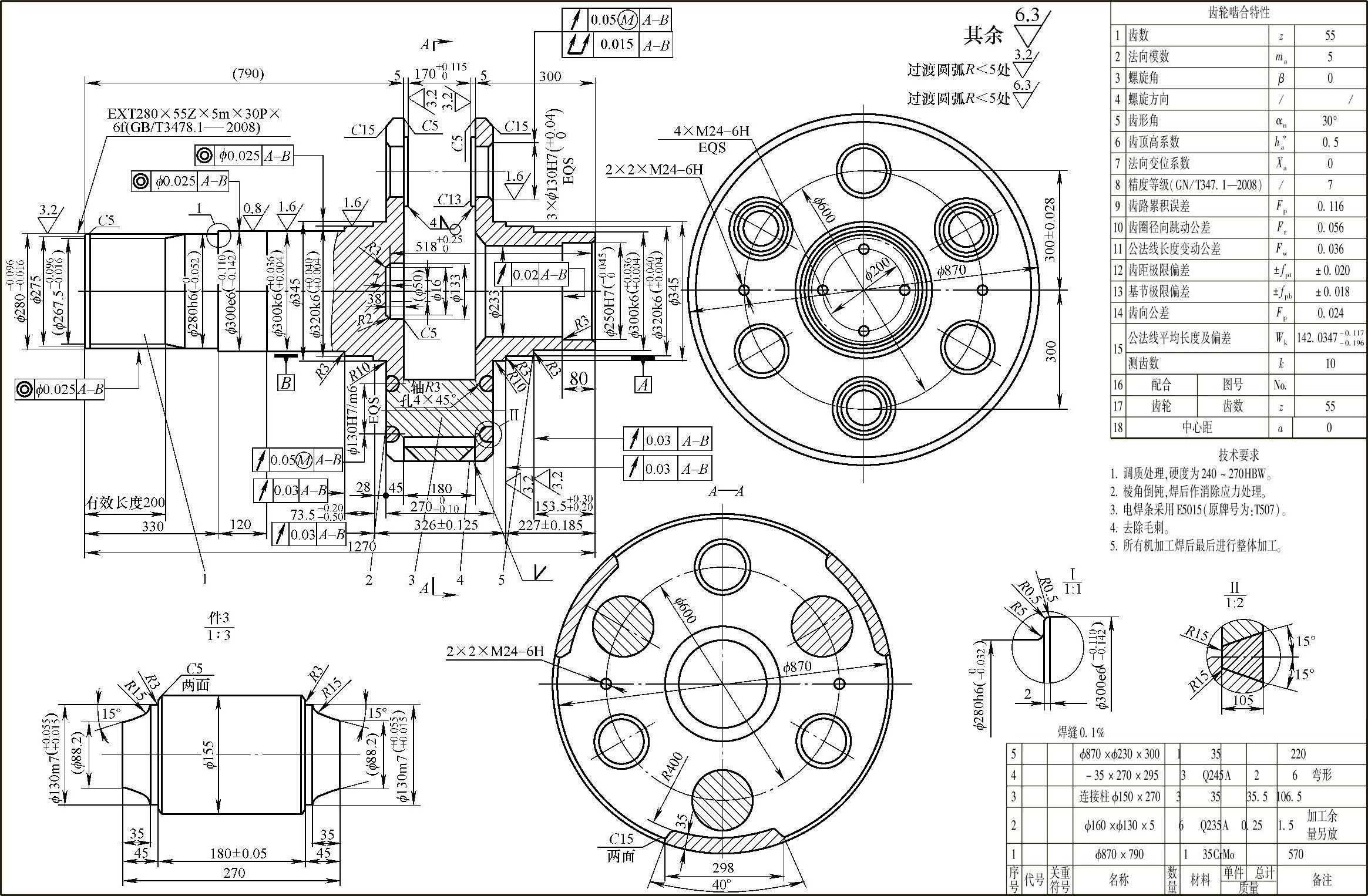
图8-81 焊接结构的行星架（三）