双排2K-H型行星轮系包括负号机构NW型和正号机构WW、NN型，其行星轮为双联行星轮，而转化机构均为两级传动（见表8-5）。

表8-5 双排2K-H型行星传动的同心条件

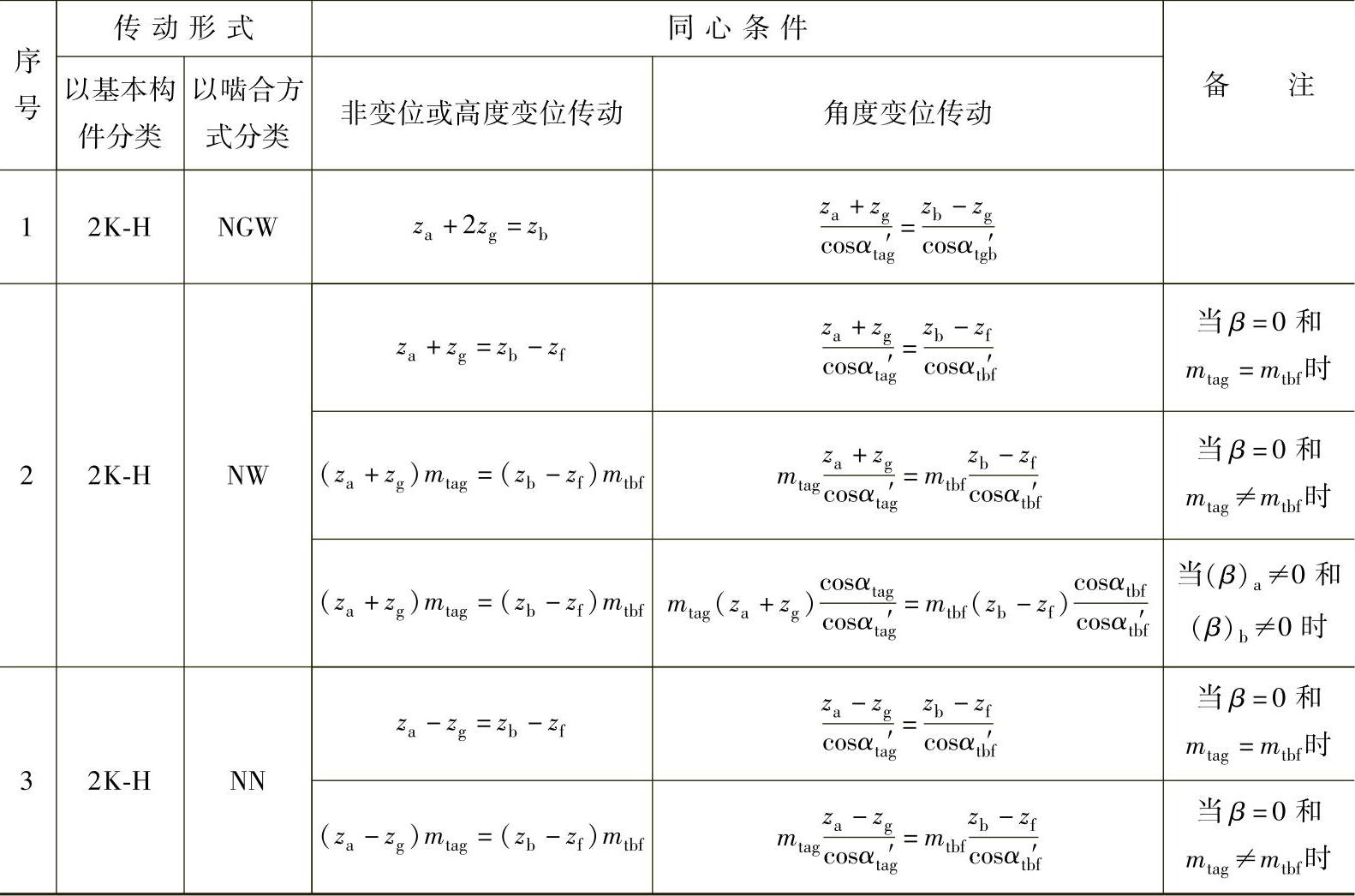
注：β——螺旋角。α_ta′_g、α_tg′_b、α_tb′f、…分别为a—g副、g—b副、b—f副、…的端面啮合角。m_tag、m_tbf

分别为a—g副、b—f副的端面模数。

其配齿数时的已知条件为：传动比i^b_aH或i^b_Ha行星轮个数n_p=3，是否要求变位，n_p个双联行星轮中两齿圈的相互位置是否都加工成一样，以及结构设计对两对齿轮副径向轮廓尺寸的比例要求等。

配齿时的约束条件，对一般传动，其传动比条件仍然不必很准确。其同心条件：对非角度变位传动要满足两对齿轮副的齿数和相等；对角度变位传动，其两对齿轮副的齿数和可以相差1～2个齿，通过角度变位凑中心距方法来满足同心条件。其装配条件；对于只有一个行星轮，以及虽有n_p个行星轮，但其装配时可分别调整两齿圈相互间的角度位配时，或者可以依靠装配要求分别对n_p个行星轮进行两齿圈角度错位加工的，在配齿数时可不必考虑装配条件，除此之外，仍须满足装配条件，而其邻接条件一般是在配齿数之后再行校核。

双排2K-H（NW、WW、NN）型行星传动，同心条件见表8-5，装配条件和邻接条件见表8-6。

表8-6 双排2K-H型行星传动的装配条件和邻接条件

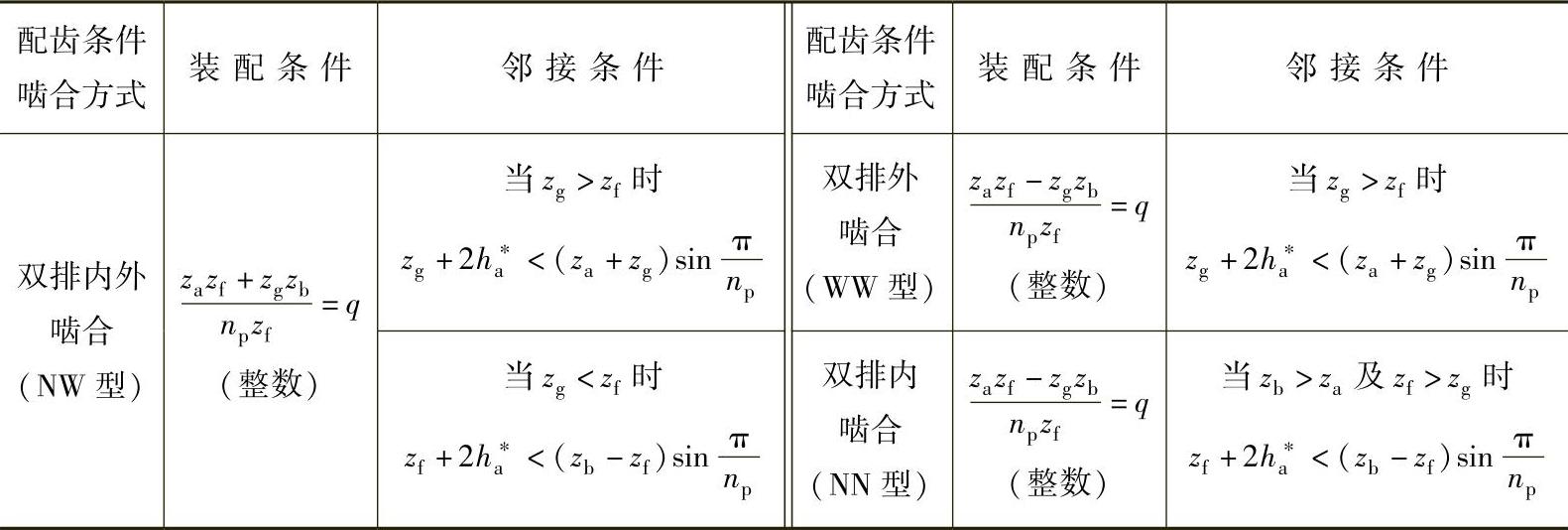
注：表中h^*_a——齿顶高系数。

对这些型号的行星轮系配齿数很灵活，方法很多，下面按其型号分别介绍几种简便易行的配齿数方法。

（1）NW型行星传动的配齿数方法

这里介绍需满足装配条件的一种简便配齿数方法。

1）配齿公式

①根据传动比条件

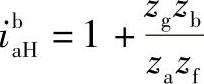
令

代入传动比公式，得

②根据非角度变位传动的同心条件

z_a（1+i₁）=z_f（i₂-1）

移项得

z_f=βz_a （8-33）

式中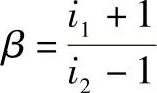

③满足结构设计要求，即两对齿轮副径向轮廓尺寸比值γ，如图8-12所示。

a—g齿轮副的径向轮廓尺寸

L₁=mz_a（1+2i₁）

b—f齿轮副径向轮廓尺寸

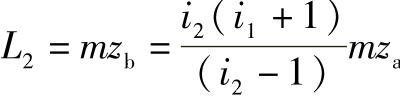
所以

分别以i^b_aH和α作为第1，2变量，代入式（8-33）和式（8-34），可计算相应的γ比值，绘成线图，如图8-13所示。

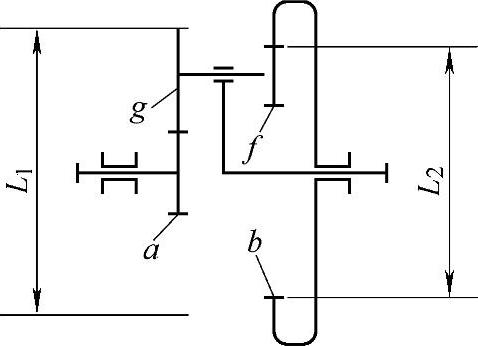
图8-12 NW型行星传动

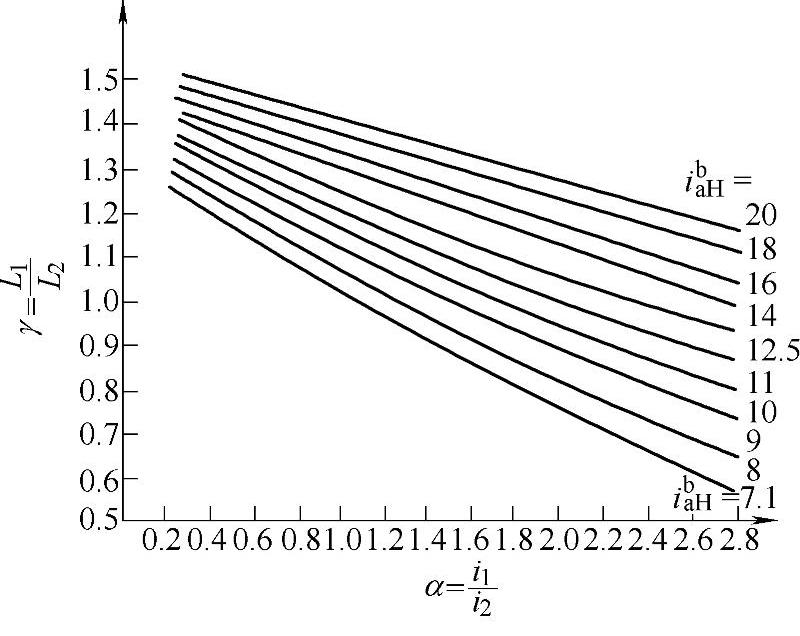
图8-13 确定γ值线图

当已知传动比i^b_aH及结构设计要求的比值γ，则从图8-13可查得相应的α系数。

④装配条件应满足式（8-28）

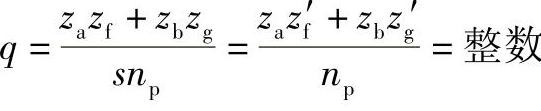
要满足这个装配条件的简便方法是分别凑使满足两个限制条件：

第一限制条件：在z_a，z_f′和z_b，z_g′中，分别有一个齿数应为n_p的倍数，简便的作法是先主动取中心轮z_a为n_p的倍数，再凑使z_b或z_g′为n_p的倍数。

第二限制条件：凑使z_g′和z_f′两齿数中，至少应有一个齿数与n_p互为质数。

⑤最后按所凑配确定的齿数，查表8-6校核邻接条件。

2）配齿数步骤

①与NGW型一样，根据强度、运转平稳性和避免根切等条件确定太阳轮齿数z_a，为了使配齿数简便起见，常取z_a为n_p的倍数。

②根据结构设计要求，先拟定γ比值，并由传动比i^b_aH及齿数z_b、z_g，计算齿数。其计算公式如下：

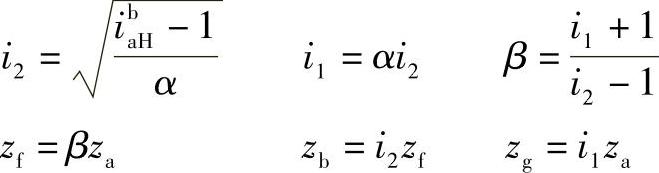
③根据计算的齿数，按装配要求的两个限制条件靠近圆整为确定齿数。为了使确定的齿数仍满足同心条件，可以让一个行星轮的齿数最后确定，并且在确定这个齿数时，要同时考虑同心条件。也就是，对非角度变位齿轮传动，z_g=z_Σ-z_a，或z_f=z_b-z_Σ；对角度变位齿轮传动，z_g=zΣ-z_a-Δz，或z_f=z_b-zΣ-Δz。上式中Δz是角度变位时要求齿数z_g或z_f中的一个减少1～2个齿。

④校核传动比及查表8-6校核邻接条件。

（2）WW型行星传动的配齿数方法

WW型行星传动属于正号机构2K-H型，其传动比可正可负，而且范围很广，其配齿数可以各种各样，很灵活，配齿数方法很多。这里分别介绍适用于小传动比、大传动比和公共行星轮用的三种简便配齿方法。

1）第Ⅰ种方法——适用于多个行星轮，需要满足装配条件和小传动比（i^b_Ha＜50）的配齿数方法。

①配齿公式

a.同心条件

z_a+z_g=z_b+z_f

令

z_g=z_f-e （8-35）

代入同心条件式，得

z_b=z_a-e （8-36）

式中，e为两个行星轮或两个中心轮的齿数差值，e值也表示a—g副与b—f副两对齿轮副径向轮廓尺寸的差值。因而e值大小可以由结构设计要求来确定。

b.传动比条件

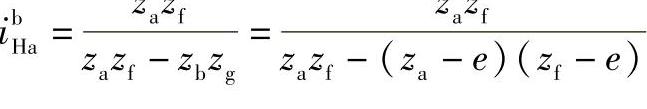
移项化简，得

令上式中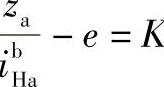

K，则得

式中K为计算常数。

c.装配条件与邻接条件和NW型行星传动作法一样。

由于WW型的两对齿轮副均为外啮合副，可以同时进行角度变位。因而，配齿数时，可尽量按标准传动的同心条件配齿数。

传动比i^b_Ha为负值，配齿数时i^b_Ha、K、e均取为负值。

②步骤

a.确定齿数差e和计算常数K，e一般可取1～8的整数；分析式（8-37b），为了避免z_f为负值或太大，应取K≥0.5。

从最紧凑观点出发，最好取K=1及e=1。

b.计算齿数：z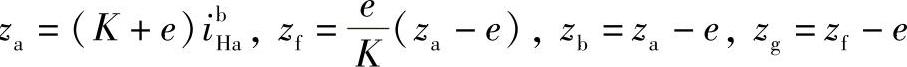

当K=1、e=1时，z_a=±zi^b_Ha，z_f=z_b=z_a∓1，z_g=z_f∓1=z_a∓2

式中“±”号，上面符号用于正传动比，下面符号用于负传动比。

c.确定齿数主要按照装配条件，其作法与NW型行星传动一样。

当K=1、e=1时，只要凑使z_a为n_p的倍数加1，即满足装配条件。

d.校核传动比及查表8-6校核邻接条件。

2）第Ⅱ种方法——适用于大传动比（i^b_Ha＞50），不一定满足装配条件的配齿方法。

这种配齿数方法，主要满足传动比条件进行配齿数。它不能满足非角度变位传动的同心条件，一般两对齿轮副的齿数和相差2个齿，依靠角度变位来满足同心条件。它只能满足某些数相关的n_p值的装配条件，而对规定的n_p值，不一定能满足其装配条件，这只能依靠双联行星轮两齿圈的角错位加工和装配前的分别调整或只用一个行星轮来避开配齿数时的装配条件。其邻接条件仍可以按表8-4进行校核。

①配齿公式

主要根据传动比条件

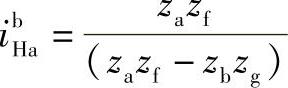
为了获得较大的传动比，其分母z_az_f-z_bz_g值应尽量小，显然，其值最小为1。令

代入传动比条件式，得

z_a（z_a+δ-1）=δi^b_Ha

求解得

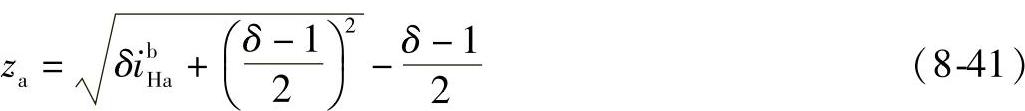
由式（8-41）得

z_bz_g=z_az_f^-δ=（z_a+δ）（z_f-δ）

由此解得

②步骤

a.选取δ值。δ值的选取，一般根据传动比的大小，推荐按表8-7选用。

表8-7 i^b_Ha-δ值对应表

(www.daowen.com)

当传动比i^b_Ha为正值时，δ取正值；当传动比i^b_Ha为负值时，则δ值也取负值。

b.计算确定齿数配齿公式为

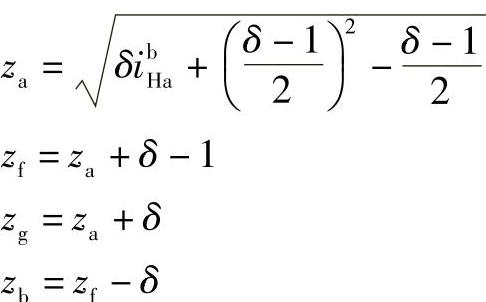
当δ=1时，其配齿公式为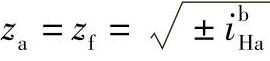（正传动比时取上面“+”号，负传动比时取下面“-”号）

z_g=z_a+δ

z_b=z_f-δ

当需要满足装配条件时，仍按装配第一、第二限制条件校核。

c.校核传动比

i^b_Ha=z_az_f/δ

这种配齿数方法所得到的各齿轮齿数，相差不大，均能满足邻接条件。

3）第Ⅲ种方法——适用于i^b_Ha＜50，公共行星轮的WW型行星传动的配齿数方法。

为了制造方便，取两个同样齿数的行星轮即z_g=z_f，并使两个中心轮齿数相差1～2个齿，故又称为公共行星轮WW型，或称少齿差WW型。

配齿公式为

式中，e′为两中心轮齿数差，e′=1～2，负传动比取负值。

对一齿差WW型，不可能满足n_p≠1的装配条件。因为两个行星轮齿数相等，其公约数s=z_g=z_f，则z_g′=z_f′=1，不是n_p的倍数；而两个中心轮齿数差为1，也不可能同时为n_p的倍数，所以不能满足装配第一限制条件。因此，一齿差WW型行星传动，常常只采用一个行星轮。

对两齿差WW型，由于两个中心轮齿数差为2，当z_a为偶数时，则可满足n_p=2的装配条件。因此，对二齿差WW型可以采用两个行星轮即n_p=2。

少齿差WW型两对齿轮副齿数和之差值为1～2个齿，可以用角度变位来满足同心条件。

由于少齿差WW型一般只用1～2个行星轮，因而能满足邻接条件，不必校核。

（3）NN型行星传动的配齿数方法

NN型与WW型一样，传动比范围很广，配齿方法很多，这里介绍适用于多行星轮、单行星轮和公共行星轮等三种配齿数方法。

1）第Ⅰ种方法——适用于多行星轮，需要满足装配条件和小传动比的配齿数方法。

①配齿公式

a.同心条件

z_a^-zg=z_b-z_f

令z_g=z_f-e （8-44）

代入同心条件式，得

z_b=z_a+e （8-45）

式中，e为两个中心轮或两个行星轮的齿数差，也表示两对齿轮副的径向轮廓尺寸之差值。当传动比为负值时，e应取负值。

b.传动比条件

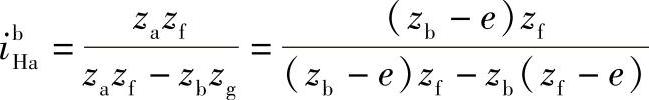
移项化简，得

或

c.满足装配条件的方法与NW型的方法一样，邻接条件可在配齿数后查表8-6进行校核。

②步骤

a.计算齿数有两种作法。

第一种作法：其计算次序为确定z_b（可根据设计要求确定）；选取齿差数值e，得

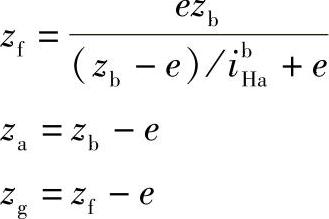
检查最小行星轮齿数是否会产生根切，检查最大行星轮是否会超过表8-4的邻接条件。当不符合要求时，应重新选取e值，重新计算，直至这两项通过为止。

第二种作法：其计算次序为确定最小行星轮齿数z_g，根据强度条件、运转平稳性条件和避免根切来确定。

选取齿数差值e得

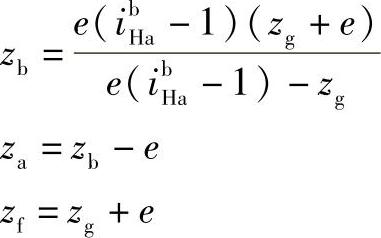
检查内齿轮齿数既不能太少（避免插齿时产生顶切），也不能太多，更不能出现负值。当不符合要求时，须重新选取e值，重新计算，直至检查通过。

b.确定齿数。在计算齿数基础上，根据满足装配条件凑整数，其方法与NW型方法一样。对一级传动为了配齿方便，常取各轮齿数及e值均为n_p的倍数；但对高速重载传动，为了保证有良好的工作平稳性，各啮合齿轮的齿数间，不应有公约数，因此，配齿数时，e值不能取n_p的倍数。

c.验算传动比及校核邻接条件。

2）第Ⅱ种方法——单个行星轮的查线图配齿数方法。

单个行星轮的NN型行星传动，不但具有内啮合提供在直径上小得多的轮廓尺寸，而且由于内啮合中心距小，具有较小的行星轮离心力，为了充分获得这两个优越性，应该使两对内啮合传动中的齿数差值即z_b-z_f和z_a-z_g尽可能小。

由于只有一个行星轮，因而不必满足装配条件和邻接条件，只须满足传动比条件和同心条件。

①配齿公式及线图

a.同心条件

z_b^-zf=z_a-z_g=z_Σ （8-48）移项得

z_b^-za=z_f-z_g=e （8-49）

式中 z_Σ——齿数和；

e——两个行星轮或两个中心轮的齿数差。

b.传动比条件

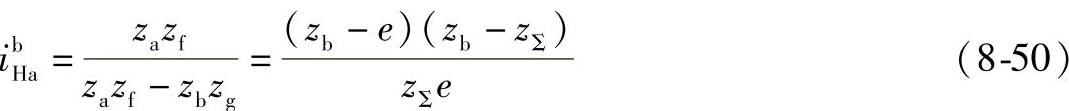
移项得

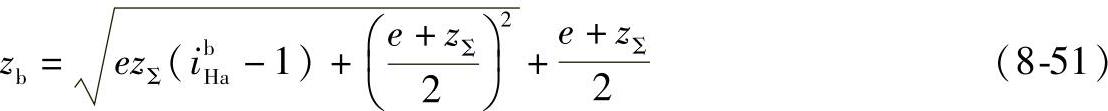
根据式（8-50）或式（8-51），可以绘出如图8-14所示的线图。这线图可方便地被应用来选配齿数。

②步骤。根据已知传动比i^b_Ha及预选的zΣ、e，查线图8-14得z_b，进而计算其他齿轮齿数，其公式为

z_a=z_b-e，z_f=z_b-z_Σ，z_g=z_f-e

为了获得最小的尺寸及重量，对齿数差e应尽量选取得小些。

对z_Σ值的选取，当采用齿形角α=20°的标准齿轮传动，为了避免齿顶干涉，应按内齿轮齿数z₂查图8-14选取。当超过上述规定时，可通过角度变位或缩小齿顶高来避免齿顶干涉。

对齿形角α=30°的特殊刀具，其标准传动时的齿数和zΣ可以等于3。

例8-11 已知NN型行星传动传动比i^b_Ha=1200，试配齿数。

解 由i^b_Ha=1200查图8-14，选取zΣ=3，e=2，可得z_b=88。

z_a=z_b-e=88-2=86

z_f=z_b-z_Σ=88-3=85

z_g=z_f-e=85-2=83

校核传动比

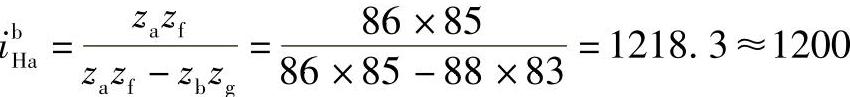
结果：z_a=86 z_b=88 z_g=83 z_f=85 i^b_Ha=1218.3

3）第Ⅲ种方法——单个行星轮的简化配齿数方法。

这个方法对不同的传动比范围，推荐其相应的齿数和zΣ；

当10000＞i^b_Ha＞2500 zΣ=1

当2500＞i^b_Ha＞1000 zΣ=2

当1000＞i^b_Ha＞400 zΣ=3

当400＞i^b_Haz_Σ=4

这个方法对不同的传动比范围，推荐不同的简化配齿公式：

①i^b_Ha＞400时，取z_Σ=e可得

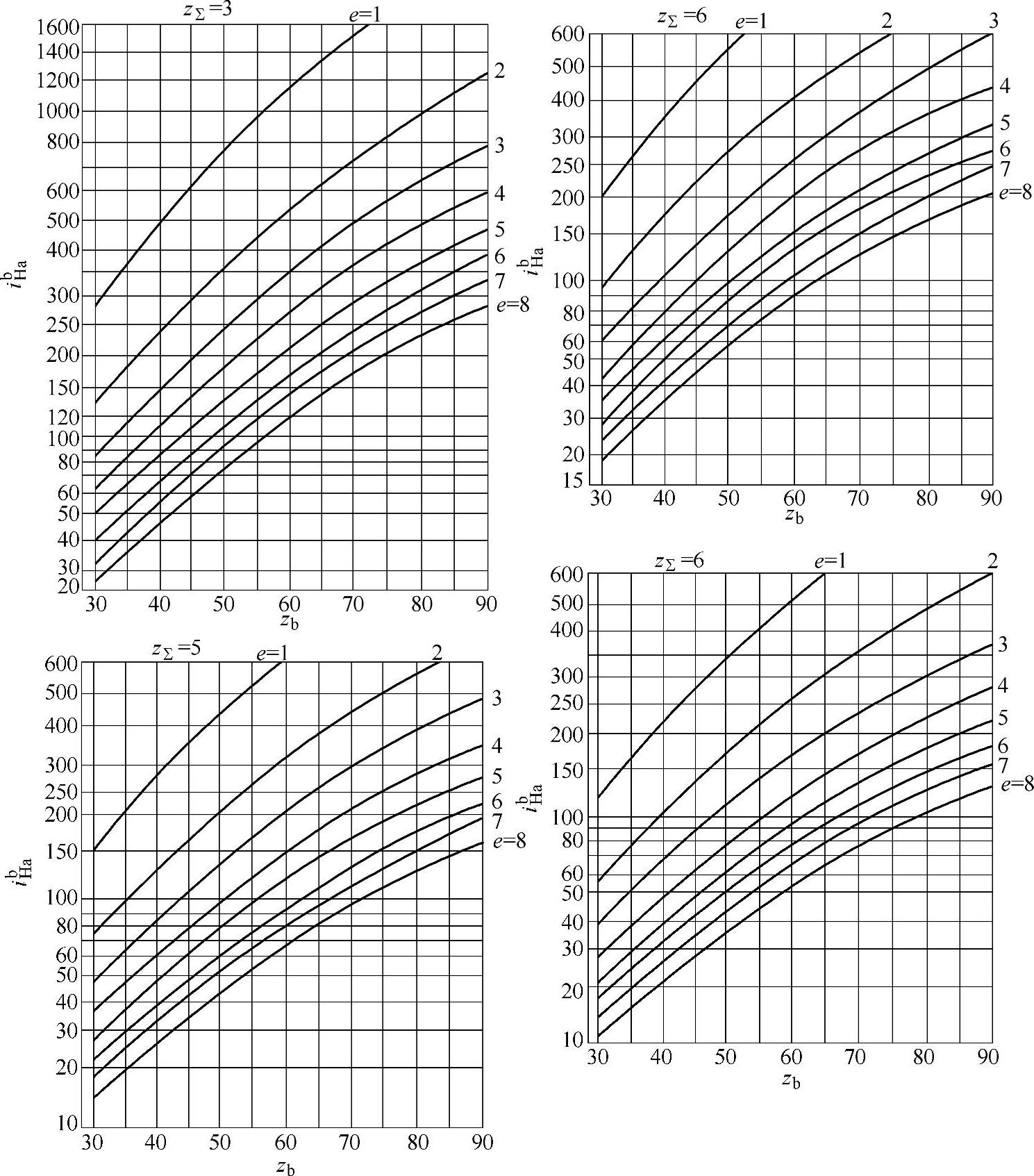
图8-14 根据给定的i^b_Ha、z_Σ和e值确定z_b的线图

对负传动比，即i^b_Ha<-400时，取z_Σ=-e，同理可得

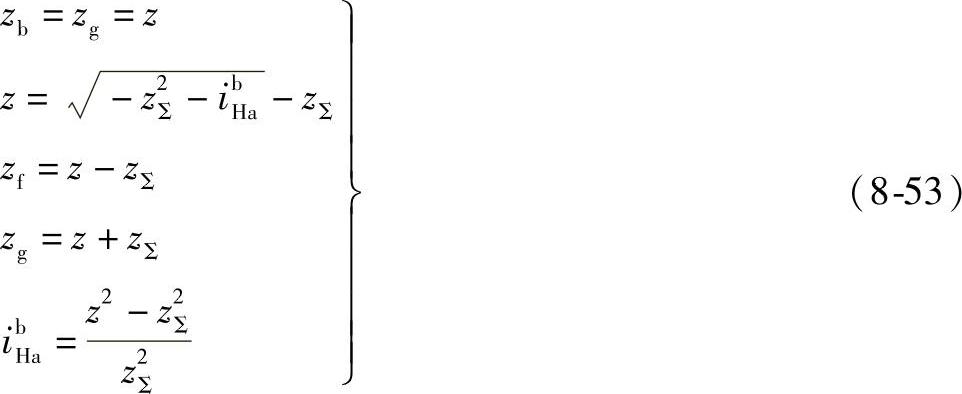
②100＜i^b_Ha＜400时，令z_f-z_a=e，则

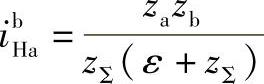
移项得

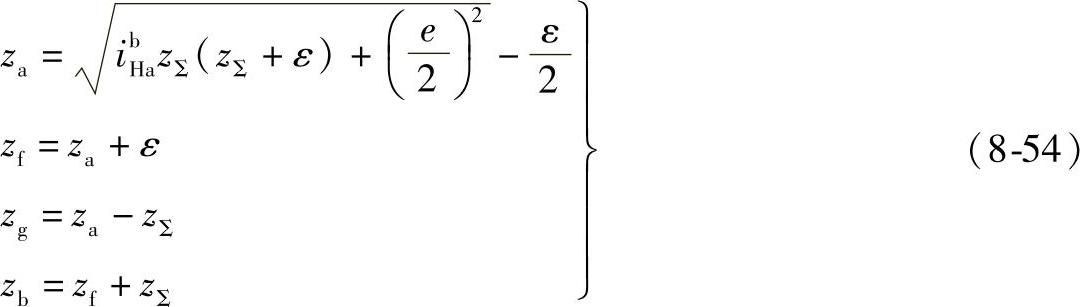
正传动比时，取ε=1～4，

负传动比时，取ε=-（2_zΣ+1～4）。

③20＜i^b_Ha<100时，为了制造方便，将两个行星轮的齿数取为一样，即z_g=z_f，并使两个中心轮齿数差为1个，这就成为“一齿差NN型”，或称为公共行星轮的NN型行星传动。

其配齿公式为

式中，zΣ为齿数和。为了避免齿顶干涉，zΣ应根据最小内齿轮齿数z₂，由表8-8选取。

式中的正负符号，正传动比取上面的符号，负传动比用下面的符号。

表8 - 8zΣ的选取