设计行星齿轮传动时，其齿数的选配除了满足所需的传动比之外，同时还应满足同心条件、装配条件和邻接条件，有时还应考虑一些其他的附加条件。

（1）传动比条件

1）2K-H（NGW）型

i^b_aH=1-i_a^Hb=1+z_b/z_a

所以

z_b=（i^b_aH-1）z_a （8-17a）

式（8-17a）为满足传动比条件的第一种表达关系式，令

x=z_ai^b_aH

则z_b=x-z_a （8-17b）

由式（8-17b）中可以看出，x值必须为整数值。

满足传动比条件的第三种表达关系式为

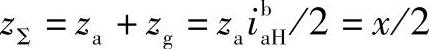
即

2）2K-H（NW、WW、NN）型

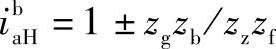
负号机构NW型用“+”号，正号机构WW、NN型用“-”号。

负号机构NW型传动比条件式为

正号机构WW、NN型传动比条件式为

（2）同心条件

对2K-H型行星传动，其三个基本构件的旋转轴线必须重合于主轴线，即其中心轮与行星轮组成的所有啮合副的实际中心距必须相等。

1）2K-H（NGW）型 非角度变位齿轮传动：

由中心距相等

a_ag=a_gb

m/2（z_a+z_g）=m/2（z_b-z_g）

得满足同心条件第一种表达关系式为

或

式（8-19a）表明，对非角度变位齿轮传动，要满足同心条件，则两个中心轮的齿数应同为奇数或偶数，行星轮齿数等于两中心轮齿数差之半。

满足同心条件的第二、三种表达关系式为

式（8-19b）表明，要满足非角度变位齿轮传动的同心条件，X值必须为偶数。

角度变位齿轮传动：由于角度变位齿轮传动，其实际中心距并不等于标准齿轮传动的中心距，因而其同心条件不受式（8-19）的限制，即不必受两个中心轮同为奇数或偶数的限制，也不必受X值一定要为偶数的限制，而只要满足两对啮合副的实际中心距相等条件

α_a′_g=α_g′_b （8-20a）或

（z_a+z_g）/cosα_a′_g=（z_b-z_g）/cosα_g′_b （8-20b）

式中，α_a′_g、α_g′_b分别为a—g副、g—b副的啮合角。

由此可见，角度变位使2K-H（NGW）型行星齿轮传动齿数选配的灵活性扩大了。

2）2K-H（NW、WW、NN）型 非角度变位齿轮：由中心距相等

a_ag=a_fb按两对啮合副的模数相等，可得

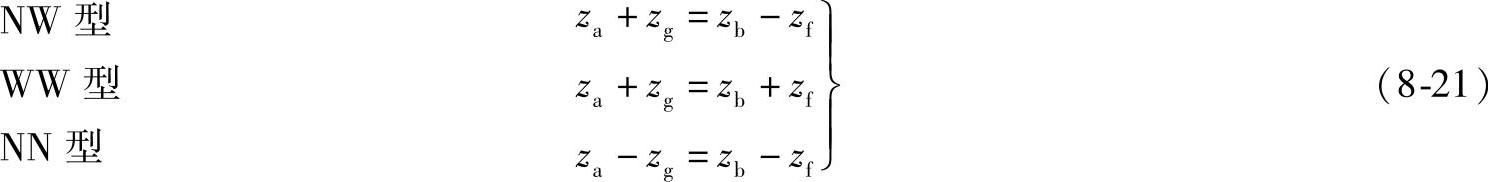
对NN型，要满足非角度变位的同心条件，其两个内齿中心轮的齿数差必须等于相应啮合行星轮的齿数差。

对WW型，要满足非角度变位的同心条件，其两个外齿中心轮的齿数差必须等于相应啮合行星轮的齿数之反差。

角度变位的齿轮传动；与NGW型一样，不需要满足式（8-19）的限制，而只要使两对啮合副的实际中心距相等即可

a_a′_g=a_f′_b （8-22）

（3）装配条件

1）NGW型 欲使数个行星轮均匀地配置在中心轮周围，而且都能嵌入两个中心轮之间，如果行星轮的个数与各齿轮齿数没有满足一定的关系，这些行星轮是装不进去的。因为当第一个行星轮装入之后，两个中心轮的相对位置就确定了，这时按平均布置的其他行星轮在一般情况下就不可能嵌入两个内、外齿中心轮之间，即无法进行装配。为了保证能够装配，设计时必须满足行星轮个数与各齿轮齿数之间符合一定关系的要求，这就称为装配条件。

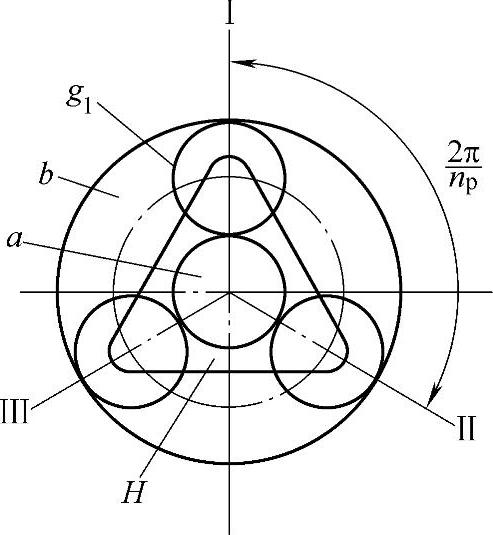
图8-5 NGW型行星齿轮传动的装配条件

设n_p为行星轮个数，则行星架上相邻两个行星轮间所夹的中心角为2π/n_p，如图8-5所示。设在位置Ⅰ装进第一个行星轮g₁，与两个中心轮a、b相啮合，然后将行星轮转过2π/n_p角度，使第一个行星轮g₁转到位置Ⅱ。由于行星架H转动而带动中心轮a也转动，这时，轮a所转动角度

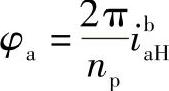
为了能在位置Ⅰ再装进第二个行星轮g₂，则要求中心轮a在位置Ⅰ的轮齿位置应该与它转过φ_a角之前在该位置的轮齿位置完全相同，也就是说，φ_a角必须刚好是中心轮a相邻两齿所对应的中心角2π/z_a的倍数，即

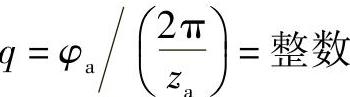
将φ_a代入上式并化简，得

q=z_ai^b_aH/n_p=（z_a+z_b）/n_p （8-23a）

式（8-23a）为NGW型满足装配条件的第一种表达关系式。显然，n_p与z_a、z_b只要满足式（8-23a），就可以在位置Ⅰ装进第二个行星轮g₂；同理，可以装进第三个行星轮……第n_p个行星轮。式（8-23a）表明：NGW型行星齿轮传动的装配条件为两个中心轮的齿数之和应为行星轮个数n_p的整数倍。

NGW型装配条件的第二、三种表达关系式为

式（8-23b）表明：NGW型装配条件为x值必须是行星轮个数n_p的整数倍。

式（8-23c）表明：NGW型装配条件为2zΣ值必须是行星轮个数n_p的整数倍。

不管是否为角度变位齿轮传动，其装配条件的关系式都是一样的。

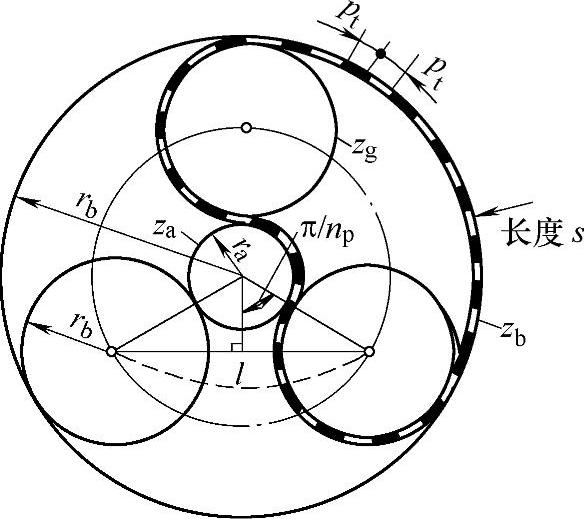
图8-6 行星轮装配条件推导简图

行星轮的装配条件也可用图示的方法（图8_-6）进行推导，在图中假如将长度为s的黑白交替纹路的胶带如图8-6所示装在内齿圈、两个行星轮、太阳轮上，使其转动，则长度s应为齿距p_t（节距）的整数倍。因此，n_p个行星轮绕太阳轮等距离装配时，则

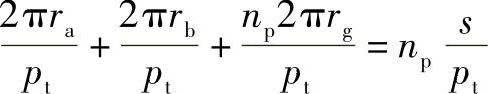
所以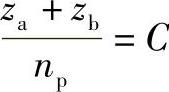(www.daowen.com)

式中，s/p_t、C为整数值。因此，太阳轮和内齿圈的齿数和必须是行星轮个数n_p的整数倍。

r_a、r_g、r_b为齿轮a、g、b的分度圆半径。

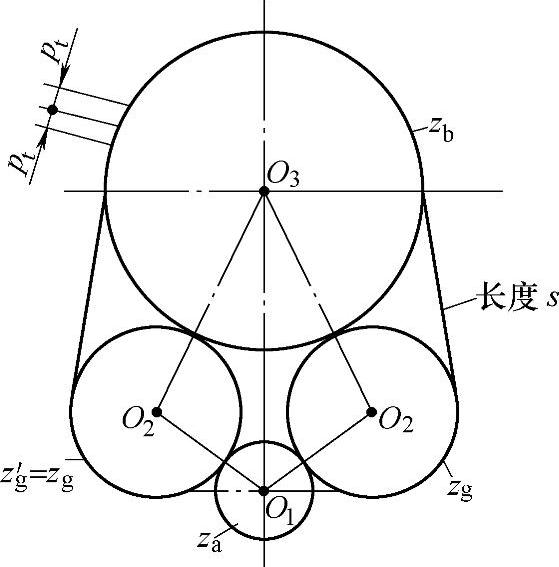
图8-7 先分流后合成传动的装配条件

对于有时进行功率分流，然后再合成，由一大齿轮输出，同时也应满足上述装配条件，否则两侧齿轮中，其中一件无法进行装配。同理，推导如下（图8-7）：

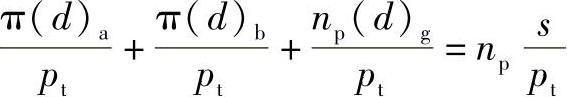
则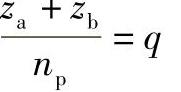

式中 （d）a、（d）b、（d）g——齿轮a、b、g分度圆直径；

p_t——齿距（节距）；

q——整数；

z_a、z_b、z_g——齿轮的齿数。

通常n_p=2，只需满足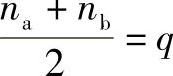便可。

同时，也应满足邻接条件。

若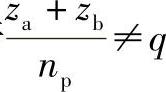（整数时），为了使行星轮的装配尽可能接近于均布，则取q′值接近于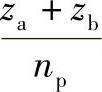的整数值。

于是，行星轮不能均布的安装角β，其计算步骤如下：

①计算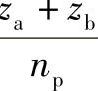，取接近于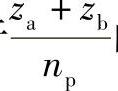的整数值q′。

②计算安装角β，

。

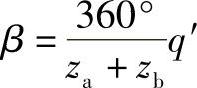
③若q′与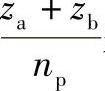差值较大时，求出的β后应校核邻接条件。

例8-9 已知z_a=22，z_b=60，行星轮个数n_p=4，求行星轮间的安装角β。

解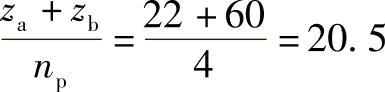

由于行星轮为非均布，取q′=20，则安装角（行星轮g₁与g₂间的夹角见图8-8）为

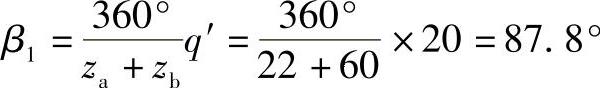
而行星轮g₂与g₃间的夹角

β₂=180°-87.8°=92.2°

2）NW、WW和NN型NW、WW和NN型行星齿轮传动，其行星轮为双联齿轮。如果n_p个行星轮的双联齿圈的相互位置不一样，就无法装配。若用错位加工的行星轮或在装配时才确定的，则其配齿数时不受装配条件的约束，只要满足传动比条件、同心条件和邻接条件即可。而当n_p个行星轮的双联齿圈的相互位置加工成一样时，则其配齿条件同样要满足装配条件。这些类型的装配要求有两个方面：其一，从制造上要求每一个双联行星轮中的g、f两齿圈都应该有一个齿槽（或齿厚）端面对称线重合于一直线上；其二，行星轮个数与各齿轮齿数的关系应该满足装配条件的关系式，这个关系式的推导原理与NGW型相似。

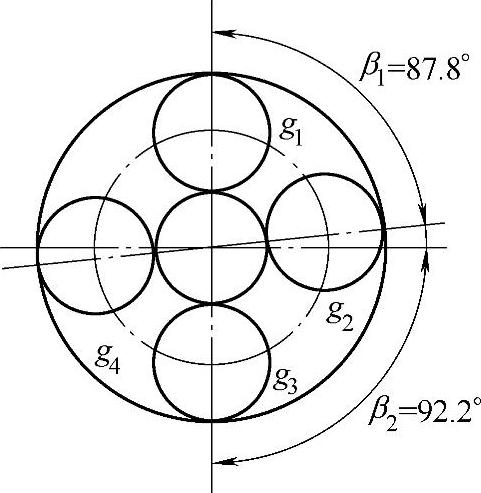
图8-8 非均布行星轮的安装角β

如图8-9a所示，设轮b固定，在位置0装入行星轮g₁，然后将行星架转过2π/n_p或转过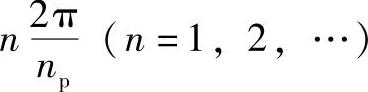，相应轮a转动角度为

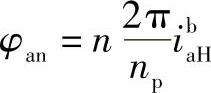
当φ_an满足

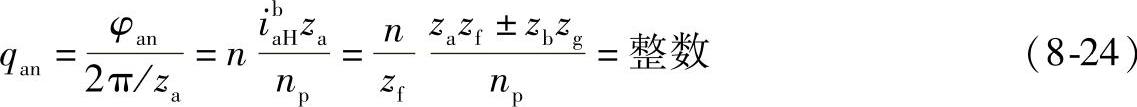
时，即行星轮g₂可以从位置0装入，同理其他行星轮均能从位置0装入。

关于n值，当为n_p的倍数时，即行星轮g₁又转回位置0，当然不能在位置0再装入其他行星轮。所以要满足装配条件，n值不能为n_p的倍数。

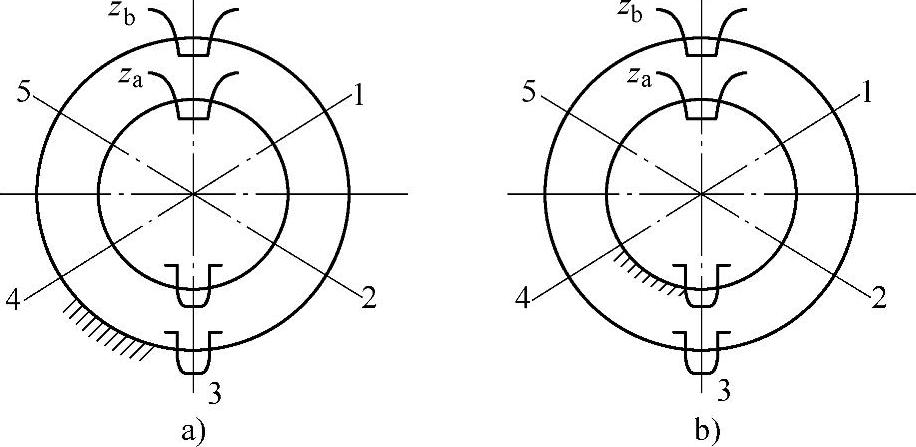
图8-9 装配条件

当n值与n_p值有公因子时，则行星轮不能全部装入，只能部分装入。例如，当n_p=6，n=15，两者有公因子3，先在位置0装入行星轮g₁，然后行星架转动15×2π/6=2.5×2π（即两圈半），在位置0可装进行星轮g₄。以后重复转两圈半时，总是行星轮g₁或g₄对准位置0，因而其他行星轮g₂，g₃，g₅，g₆都没有机会装入，所以只能部分行星轮装入。

如图8-9b所示，设轮a固定，在位置0先装入行星轮g₁，然后行星架转动m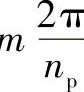，m=1，2，…，轮b相应转动角

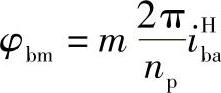
φ_bm满足

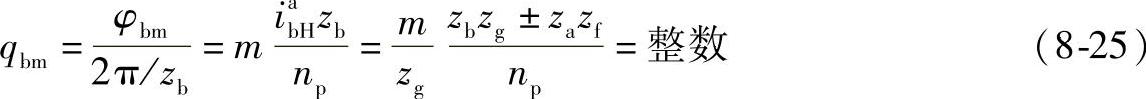
同理，式（8-25）中m值不能为n_p的倍数，当m值与n_p值有公因子时，行星轮也是只能部分装入。

综合上述两种可能的装配条件，可见：

1）当m、n两值之中，只要有一个值与n_p值互为质数，则式（8-24）和式（8-25）中就有一个式子满足装配条件。

2）如果m、n两值各有n_p值的因子，经过实践和理论分析表明，只要这两个因子互为质数，则全部行星轮均可装入，即满足装配条件。

3）双联行星轮的两个齿圈的齿数z_g、z_f，如果有公约数s，可令z_g=sz_g′，z_f=sz_f′，则式（8-24）和式（8-25）可改写为

令n=z_f，m=z_g，则q_an=q_bm=q，故得

由此，得到双联行星轮2K-H型行星轮系的装配条件有如下两个限制条件：

①满足式（8-28），即

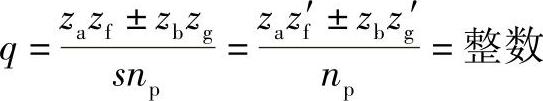
或者是当齿数z_a、z_f′与z_b、z_g′这两组数中，都有任一为n_p倍数的常数，则式（8-28）得到满足，这是第一限制条件。

②只要齿数z_f′或z_g′中，到少有一个齿数与n_p互为质数，或者当n≥6时，z_f′及z_g′分别与n_p有公因子，这两因子且互为质数，这就满足装配条件的第二限制条件。

不管是否为角度变位齿轮传动，其装配条件都是相同的，而且都需要满足。

（4）邻接条件

在行星齿轮传动中，相邻两个行星轮不相互碰撞，必须保证它们之间有一定间隙，通常最小间隙应大于半个模数，这个限制称为邻接条件。根据邻接条件，相邻两个行星轮的中心距L应大于最大行星轮的顶圆直径d_ag或d_af，如图8-10所示。

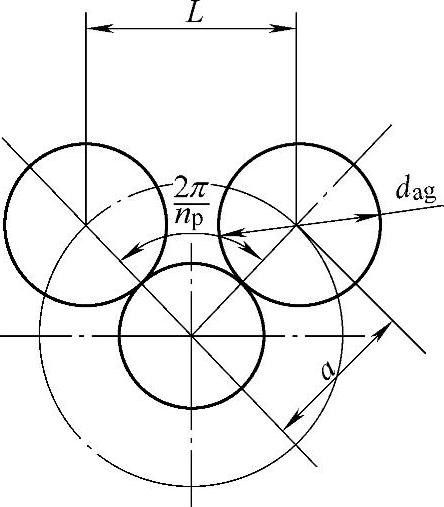
图8-10 邻接条件分析

L＞d_ag即

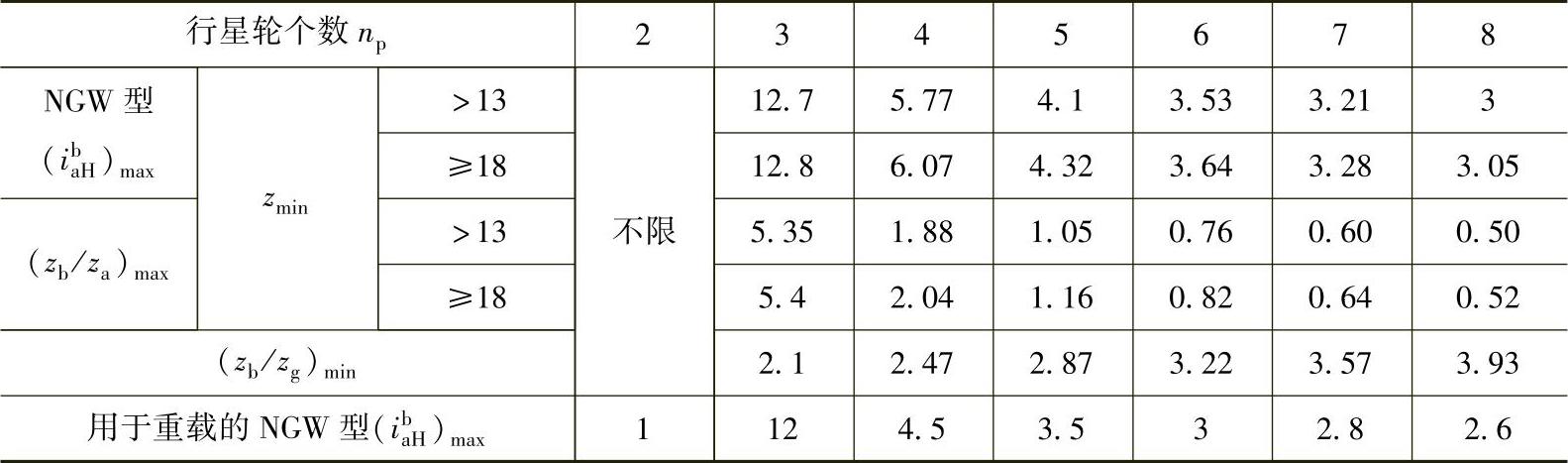
从分析NGW型中可以看出，当不断增大传动比i^b_aH，则z_g/z_a比值也不断增大，会受到邻接条件的限制；当增加行星轮个数n_p，也同样会受邻接条件的限制。所以，邻接条件限制了行星轮个数和传动比的增大。表8-4为根据邻接条件列出的对于不同行星轮个数可能达到的最大传动比，供设计时参考。表中设z_g>z_f，z_b>z_a。（z_g/z_a）max可用于NW、WW、NN型行星齿轮传动。

设计行星齿轮传动时，一般应首先确定传动比和行星轮个数，显然所确定的行星轮个数和传动比应该符合表8-4中邻接条件的要求。当所确定的传动比接近于表中相应的最大值时，仍需要在几何尺寸计算后，按式（8-29）进行邻接条件的验算，否则就毋需再验算其邻接条件了。在进行配齿数时，表8-4也可作为校核邻接条件的依据。

表8-4 根据邻接条件确定，对应行星轮个数n_p可能达到的最大传动比（i^b_aH）max，（z_g/z_a）max和（z_b/z_g）min值