(1)应用范围
本计算方法基于齿轮在低于80m/s的节线速度下运行的台架试验结果。这些公式可用于较高速度运行的齿轮,但随速度的增加也提高了不确定性,该不确定性在速度超过试验条件的范围时,与本体温度、摩擦系数、许用温度的测定有关。
1)胶合损伤 胶合损伤一旦发生,会随着功率损失、动载荷、噪声和磨损的增加,导致轮齿表面严重的破坏。如果运行条件的恶劣程度不改善,还会引起轮齿的折断。在由于瞬时过载而引起的胶合中,随着载荷的迅速降低,也即载荷的重新分配,则齿面在某种程度上可自行修复。即使如此,残留的损伤将继续成为增加功率损失、动载荷以及噪声的一个起因。
在大多数情况下,使用具有增强EP(极压)性能的润滑油能提高齿轮抗胶合能力。然而,重要的一点是要意识到使用EP油的一些不足之处:使铜腐蚀、弹性材料的脆化,以及缺乏全球通用性等。进行最佳润滑油的选择时,应考虑这些不利因素,在满足最低添加量的情况下,添加剂的用量应尽可能地少。
由于各种参数的不断变化,在瞬时接触区内化学特性与热-液-弹作用的复杂性,在计算评价胶合危险的可能性时,一些离散性必须预料到。
与疲劳损伤发展的时间相对较长不同,一个单纯的瞬时过载会产生严重的胶合损伤,以至于使齿轮不能再使用。当选择齿轮适当的安全系数时,特别对于要求在高圆周速度下运行的齿轮,应当仔细地考虑这一点。
2)积分温度准则 评价胶合概率的本方法是基于这样的假设,即当沿啮合线的接触温度平均值等于或超过一个相应的“临界值”时胶合可能会发生。在此给出的方法中,本体温度与沿啮合线的闪温积分值的加权平均的和就是积分温度。本体温度按(3)1)⑤计算,闪温的均值近似地用沿啮合线的摩擦因数、动载荷来替代。加权系数的引用要考虑实际的本体温度值与数学积分的平均闪温值对胶合现象有可能不同的影响。
使用比较积分温度与从为抗胶合能力进行的润滑油的齿轮试验(例如,各种FZG试验方法、IAE齿轮试验与Ryder齿轮试验)、或从运行中已胶合的齿轮得出的相应临界值的方法来评价胶合的概率。
(2)影响因素
1)平均摩擦因数μmc齿面间的实际摩擦因数是一个瞬时与局部的数值,它取决于油品的一些性能、齿面粗糙度,如同由加工留下的凸凹不平的位置,齿面材料的特性、切线速度、齿面的受力及几何尺寸。瞬时摩擦因数的评定比较困难,因目前尚无一种有效测定方法。
沿啮合线的平均摩擦因数μmc,可由测量得到与由公式(6-346)估计出。虽然,局部摩擦因数在节点C接近于零,当引入公式(6-346)时,其平均值可用节点的参数与油温Θoil时油的粘度ηoil大致得出。
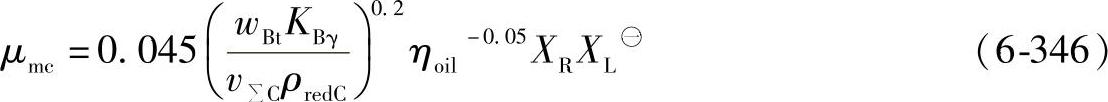
㊀ 摩擦因数的这一公式是从中心距a≈100mm的齿轮试验中得出的。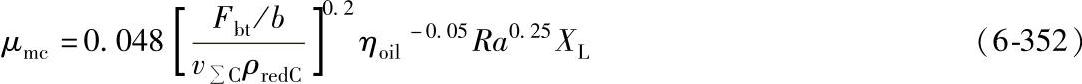
式中:
对于聚(乙)二醇: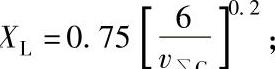
对于矿物油:XL=1.0;
对于聚α烯族烃:XL=0.8;
对于牵引液:XL=1.5;
对于磷酸酯:XL=1.3;
公式(6-352)表示在a=91.5~200mm的范围内的试验结果,应用本公式时必须相应调整关于胶合温度ΘintS的图6-109、图6-110和图6-111。
积分温度法的摩擦因数跟闪温法的摩擦因数以不同的方式考虑了齿轮的大小。计算摩擦因数的公式(6-346)仅适用下列范围,例如用于热功率的摩擦因数。
1m/s≤v≤50m/s
在分度圆线速度v低于1m/s时,摩擦因数更高,在分度圆线速度v高于50m/s时,在公式(6-346)中必须使用v=50m/s时的v∑C极限值。
wBt≥150N/mm
当单位法向轮齿载荷wBt<150N/mm时,在公式(6-346)中必须使用wBt=150N/mm的极限值。
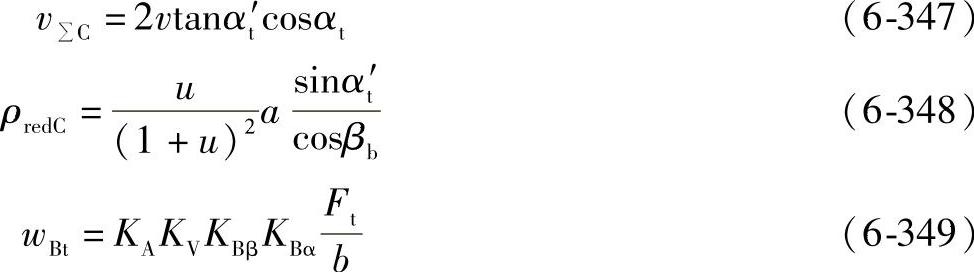
KBγ为螺旋线载荷系数,胶合考虑了由于总重合度的增加而增加的摩擦(见图6-101)。
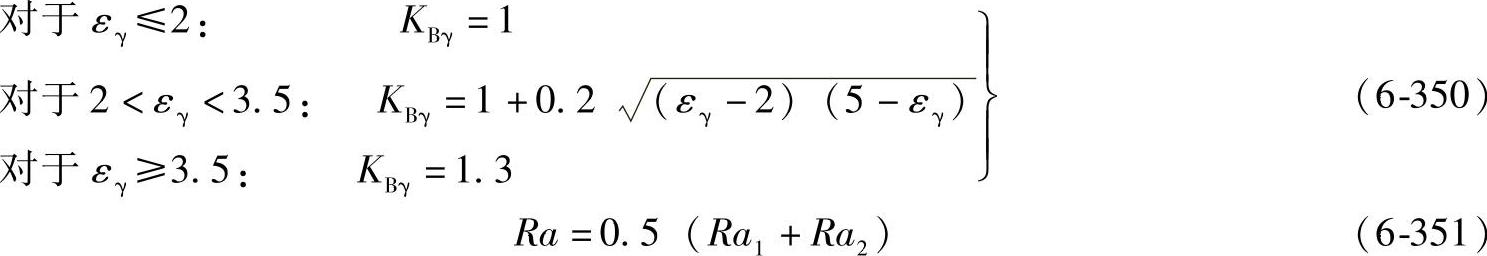
Ra1、Ra2是小轮与大轮在加工过的新齿面上测量的齿面粗糙度值(例如,标准的试验齿轮的Ra值约是0.35μm)。

式(6-346)中的XL:
对于矿物油:XL=1.0;
对于聚α烯族烃:XL=0.8;
对于非水溶性聚(乙)二醇:XL=0.7;
对于水溶性聚(乙)二醇:XL=0.6;
对于牵引液体:XL=1.5;
对于磷酸酯体:XL=1.3。
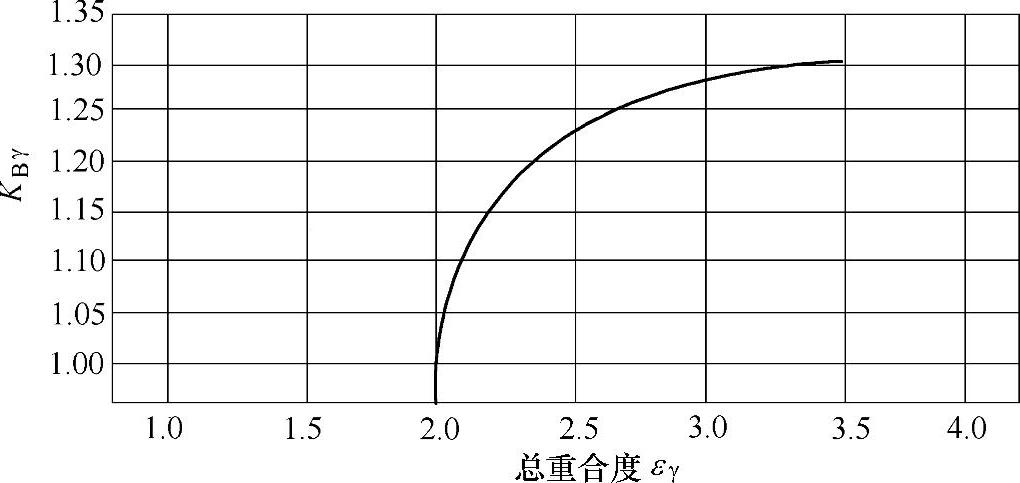
图6-101 螺旋线载荷系数KBγ
2)跑合系数XE现有的计算方法是假定齿轮已经过了较好的跑合。实际上,胶合损伤经常发生在运转开始时几个小时内,例如:齿轮箱验收时在满负荷下试验运转或一对新的齿轮装进生产设备时在适当跑合以前,齿轮在满负荷条件下运转。研究表明,与适当跑合好的齿面相比,新加工的齿面的承载能力为1/4~1/3,这要用一个跑合系数XE加以考虑。
XE=1+(1-ϕE)30Ra (6-354)
ρredC
ϕE=1,充分跑合(对于渗碳淬火与磨削过的齿轮,如果Rarun-in=0.6Ranew则可确认为已充分跑合);ϕE=0,新加工的。
3)热闪系数XM热闪系数XM是考虑小轮与大轮的材料特性对闪温的影响。
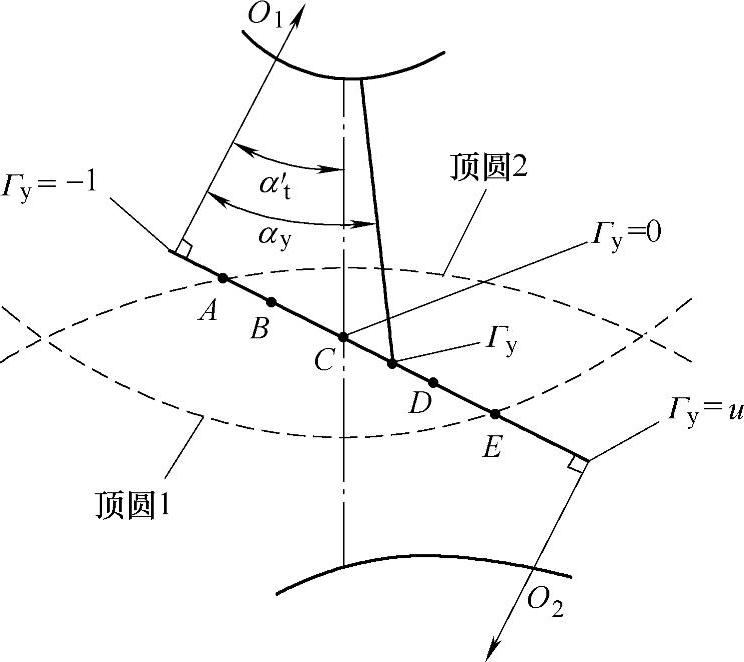
图6-102 啮合线上的参数Г
啮合线上任意点(符号y)热闪系数的计算(见图6-102):
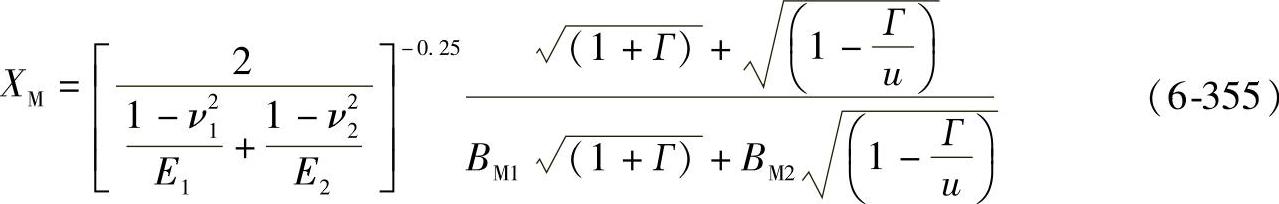

如果小轮与大轮的材料是相同的,公式(6-355)可以简化为

在上式中,热啮系数BM为

对于表面硬化钢,具有以下典型的特征值:
λM=50N/(s·K),Cv=3.8N/(mm2·K),E=206000N/mm2及ν=0.3
则
XMs=50.0K·N-0.75s0.5·m-0.5·mm
4)压力角系数Xαβ压力角系数Xαβ是用以考虑将分度圆上的载荷与切线速度转换到节圆上的系数。
方法A:系数Xαβ-A
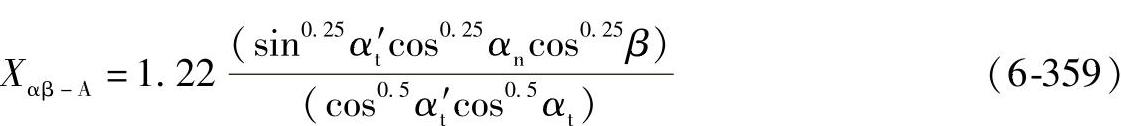
表6-39表示具有压力角为αn=20°的标准齿条的压力角系数值,标准啮合角αt′与螺旋角β的常用范围。
表6-39 方法B:系数Xαβ-B
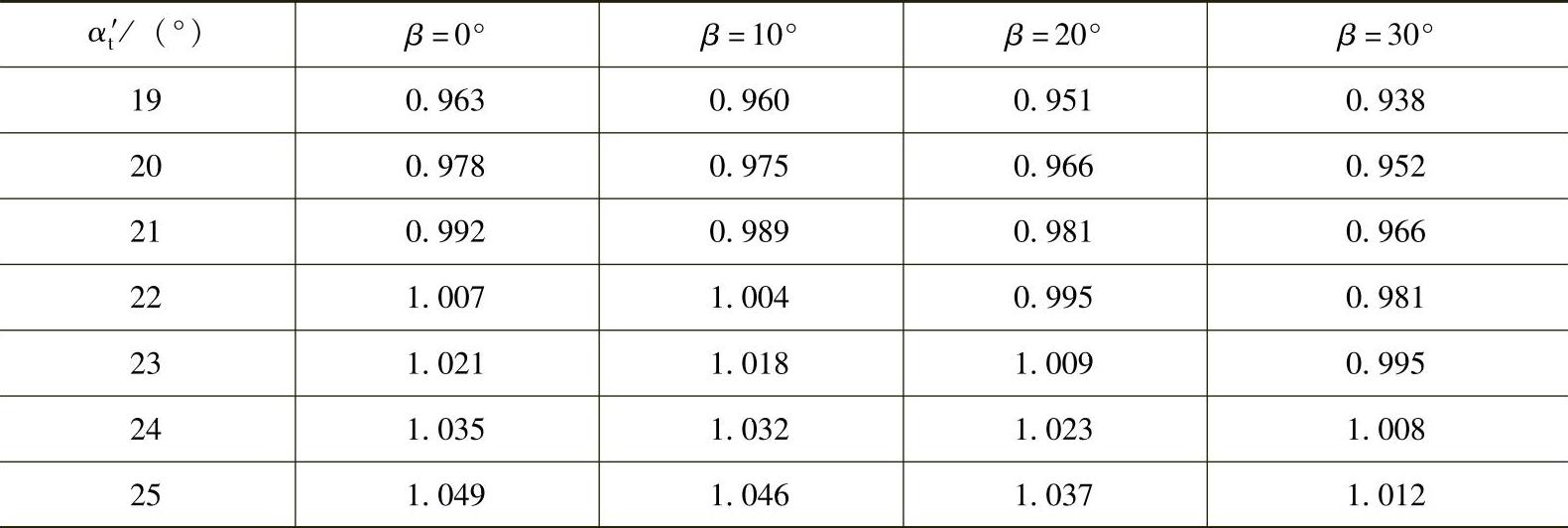
对于法向压力角为αn=20°的齿轮,作为近似考虑,其压力角系数可近似取为
Xαβ-B=1
(3)计算
1)圆柱齿轮 假定整个切向载荷在双斜齿轮的两条螺旋线之间是等量分布的。当由于有像外部轴向力这样的力的作用时,则不属于这种情况,这些力的影响必须分别考虑进去。这两条螺旋线应按平行的单斜齿轮来处理。包括影响胶合概率的各种因素可做出定量的评定。
这些公式对于具有与GB/T 1356—2001规定的基本齿条相啮的外齿或内齿齿轮均适用。对于内啮合齿轮,在确定几何系数XBE时,必须引入负值。它们也可考虑适用于端面重合度为εα≤2.5的符合其他基本齿条的类似齿轮。
① 胶合承载能力计算的安全系数SintS。当假设中的不确定性与不精确度不能排除时,有必要引入安全系数SintS。必须指出胶合承载能力计算的安全系数与温度有关,而不是这样一个系数,即用它乘以齿轮的转矩,使积分温度Θint与胶合积分温度ΘintS达到相同的数值。

SSmin的选用建议:
SSmin<1,高胶合危险。
1≤SSmin≤2,具有中等胶合危险的临界范围,受实际齿轮工作条件的影响。影响因数有例如齿面粗糙度、跑合效果、载荷系数的准确理解、润滑油的承载能力等。
SSmin>2,低胶合危险。
为给出实际载荷与积分温度数之间的关系,相应的载荷安全系数SS1可近似由下式取得:

② 许用积分温度ΘintP

要求的最小胶合安全系数SSmin对每种应用情况应分别确定。
③ 积分温度Θint
Θint=ΘM+C2Θflaint≤ΘintP (6-363)
式中 C2——由实验得出的加权系数,对于直齿与斜齿齿轮,C2=1.5。
Θflaint——平均闪温。
Θflaint=Θ flaEXε (6-364)
Xε为重合度系数。
④ 小轮齿顶的闪温ΘflaE
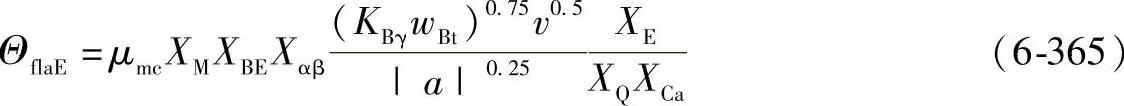
⑤ 本体温度ΘM。本体温度是即将进入啮合时的齿面温度。
本体温度是通过齿轮箱的热平衡过程而建立起来的。在齿轮箱中,有几种热源,其中最重要的是轮齿、轴承的摩擦。其他的热源例如密封与油流在某种程度上也是其中之一。当节线速度超过80m/s时,在啮合和风阻损失中因搅油而产生的热是重要的,应予以考虑(见方法A)。该热量经过传导、对流与辐射,再经箱体而传递到周围环境,对于喷油润滑,则通过油进入外部的热交换器。
用以下不同计算方法得到的数值须用下标A、B、C加以区别。
a.A法ΘM-A。本体温度作为平均值或作为齿宽上的温度分布可用实验测定或采用基于已知功率损失与传热数据进行理论分析确定,即采用热网格方法确定。
b.B法ΘM-B。此法不用于积分温度法(见本章8.4.1节闪温法)。
c.C法ΘM-A。本体温度的近似值由油温加上沿啮合线上得出的闪温平均值的(根据方法C)一部分之和来确定。

式中 XS——润滑方式系数,对于喷油润滑:XS=1.2;对于油浴润滑:XS=1.0;对于将齿轮浸没油中:XS=0.2;
C1——考虑了热转换条件的常数,试验结果为C1=0.7。
Xmp——啮合系数。

式中 np——同时啮合的齿轮的数量。
⑥ 平均摩擦因数μmc,见(2)1)。
⑦ 跑合系数XE,见(2)2)。
⑧ 热闪系数XM,见(2)3)。
⑨ 压力角系数Xαβ,见(2)4)。
⑩ 小轮齿顶的几何系数XBE。几何系数XBE考虑小轮齿顶的赫兹应力与滑动速度的影响。XBE是齿数比u与小轮齿顶E点处曲率半径ρE的函数。
对于内啮合齿轮,下面的参数必须用负值代入:齿数z2、齿数比u、中心距a以及所有的直径。
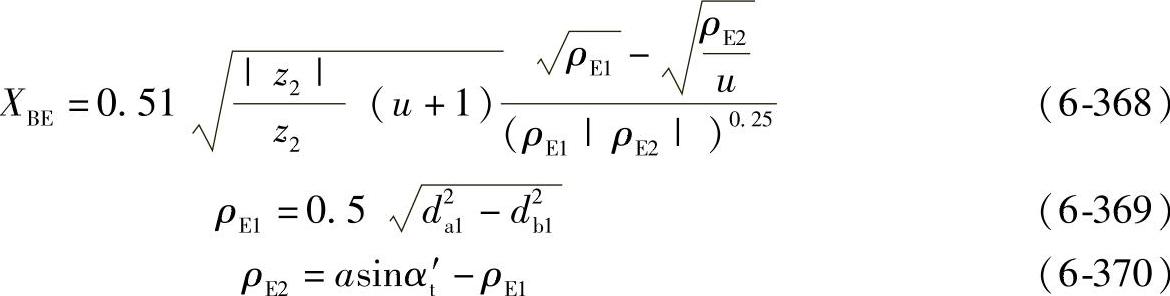
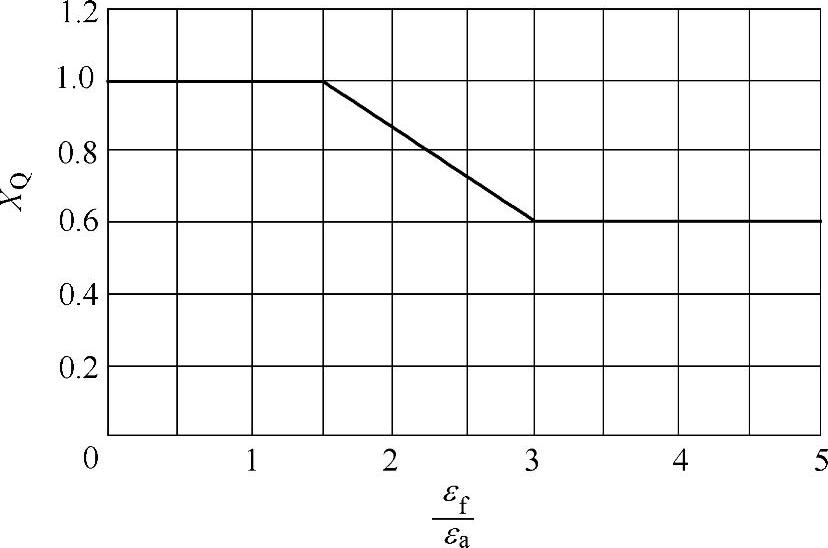
图6-103 啮入系数XQ
⑾ 啮入系数XQ。啮入系数XQ考虑了在高滑动区域,在正进入啮合处(在被驱动齿轮的齿顶处)的冲击载荷。可用啮入重合度εf与啮出重合度εa之比的函数来表示,见图6-103。
对于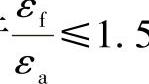 5,
5,
XQ=100 (6-371)
对于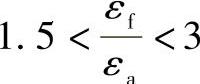 ,
,
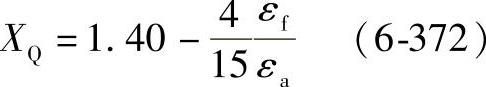
对于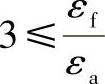
,XQ=0.60 (6-373)
当小轮驱动大轮时,
当大轮驱动小轮时,
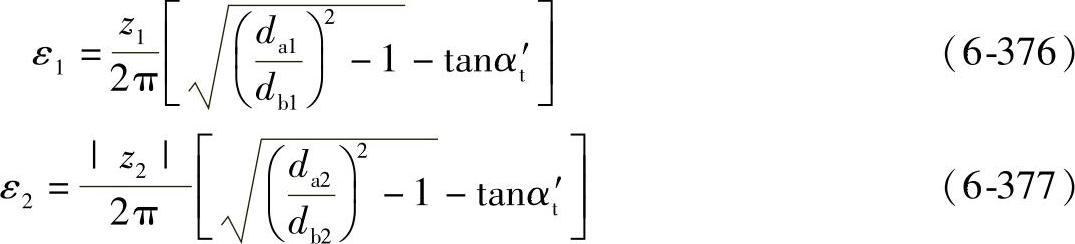
当齿顶被倒棱或倒圆时,顶圆直径da必须用啮出开始点的有效顶圆直径dNa来替代。
⑿ 齿顶修缘系数XCa。受载轮齿的弹性变形在滑动较大的齿顶处会产生高的冲击载荷。齿顶修缘系数XCa考虑了齿廓修形对这种载荷的影响。XCa是一个相对的齿顶修缘系数,它取决于相对于因弹性变形引起的有效齿顶修缘量Ceff的齿顶实际修缘量Ca,见图6-104。
图6-104 的曲线可以用式(6-378)近似确定。
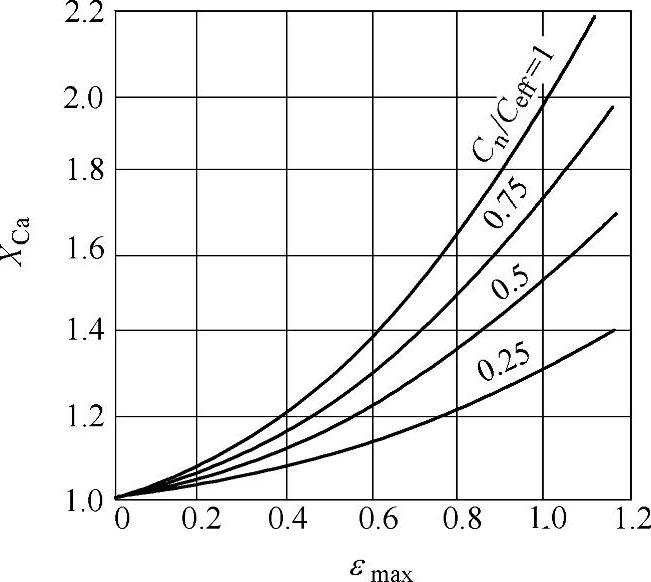
图6-104 由实验数据得出 的齿顶修缘系数XCa
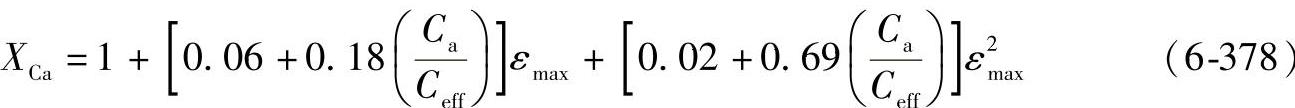
式中 εmax——ε1或ε2中的最大值。
被引入到式(6-378)的齿顶修缘的名义量Ca取决于齿顶修缘的实际值Ca1、Ca2、有效齿顶修缘量Ceff、齿顶重合度的比值及功率流的方向。
当小轮驱动大轮且ε1>1.5ε2或大轮驱动小轮且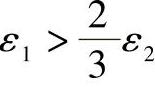 时:
时:
对于Ca1≤CeffCa=Ca1 (6-379)
对于Ca1>CeffCa=Ceff (6-380)
当小轮驱动大轮且ε1≤1.5ε2或大轮驱动小轮且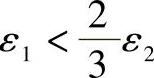 时:
时:
对于Ca2≤CeffCa=Ca2 (6-381)
对于Ca2>CeffCa=Ceff (6-382)
式中Ceff——有效齿顶修缘量,用以补偿单对齿啮合时轮齿的弹性变形。对于直齿轮 对于斜齿轮
对于斜齿轮

式中 b——齿宽,当大、小轮的齿宽不同时,取其中较小值。
上述的齿顶修缘量适用于GB/T 10095.1—2008中6级或更好的齿轮。对于低精度齿轮,规定XCa=1,也可参见GB/T 3480—1997。
⒀ 重合度系数Xε。重合度系数Xε是考虑在忽略载荷分配时,将小轮齿顶的闪温值转换为沿啮合线闪温平均值的系数。重合度系数可以用齿高重合度ε1与ε2以及它们的和εa来表示。Xε的公式是基于假定沿啮合线的闪温是线性分布的。这种方法的可能误差将不会超过5%,且偏于安全。
对于εa<1,ε1<1,ε2<1

对于1≤εa<2,ε1<1,ε2<1(见图6-105)
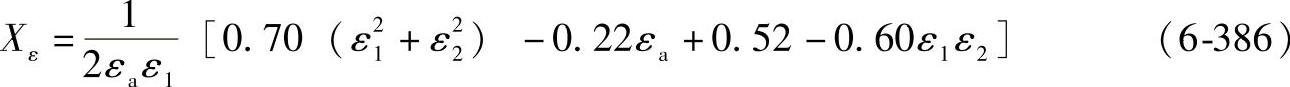
对于1≤εa<2,ε1≥1,ε2<1
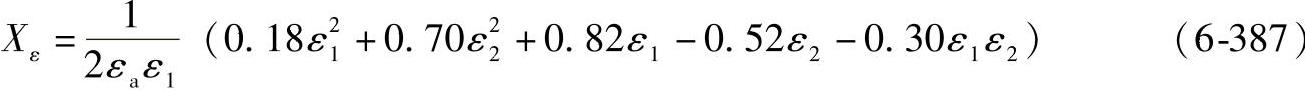
对于1≤εa<2,ε1<1,ε2≥1
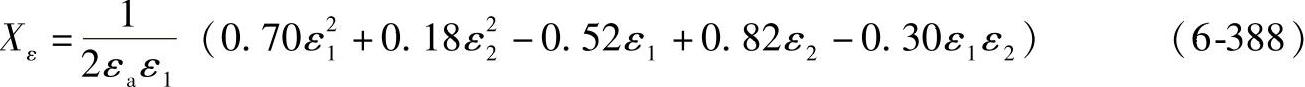
对于2≤εa<3,ε1≥ε2(见图6-106)
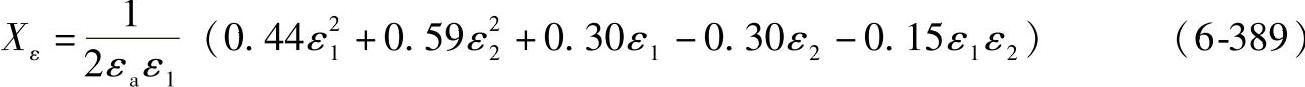
对于2≤εa<3,ε1<ε2(见图6-106)
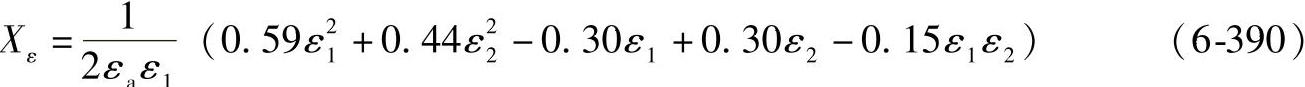
εa=ε1+ε2 (6-391)
2)锥齿轮 计算时,用锥齿轮中点直径确定的当量圆柱齿轮来近似锥齿轮(当量圆柱齿轮的计算见本章8.3.1节)。其计算方法的结构与圆柱齿轮的内容相当。
对于替代锥齿轮的当量圆柱齿轮(按锥齿轮端面内中点直径确定)的胶合承载能力,按(3)1)计算。
①胶合承载能力计算的安全系数SintS,见(3)1)①。
②许用积分温度ΘintP,见(3)1)②。
③积分温度Θint,见(3)1)③。
对于当量圆柱齿轮,C2=1.5。
④小轮齿顶的闪温ΘflaE,见(3)1)④,并采用下列替换:
——在式(6-365)中:用av代替a,vmt代替v;
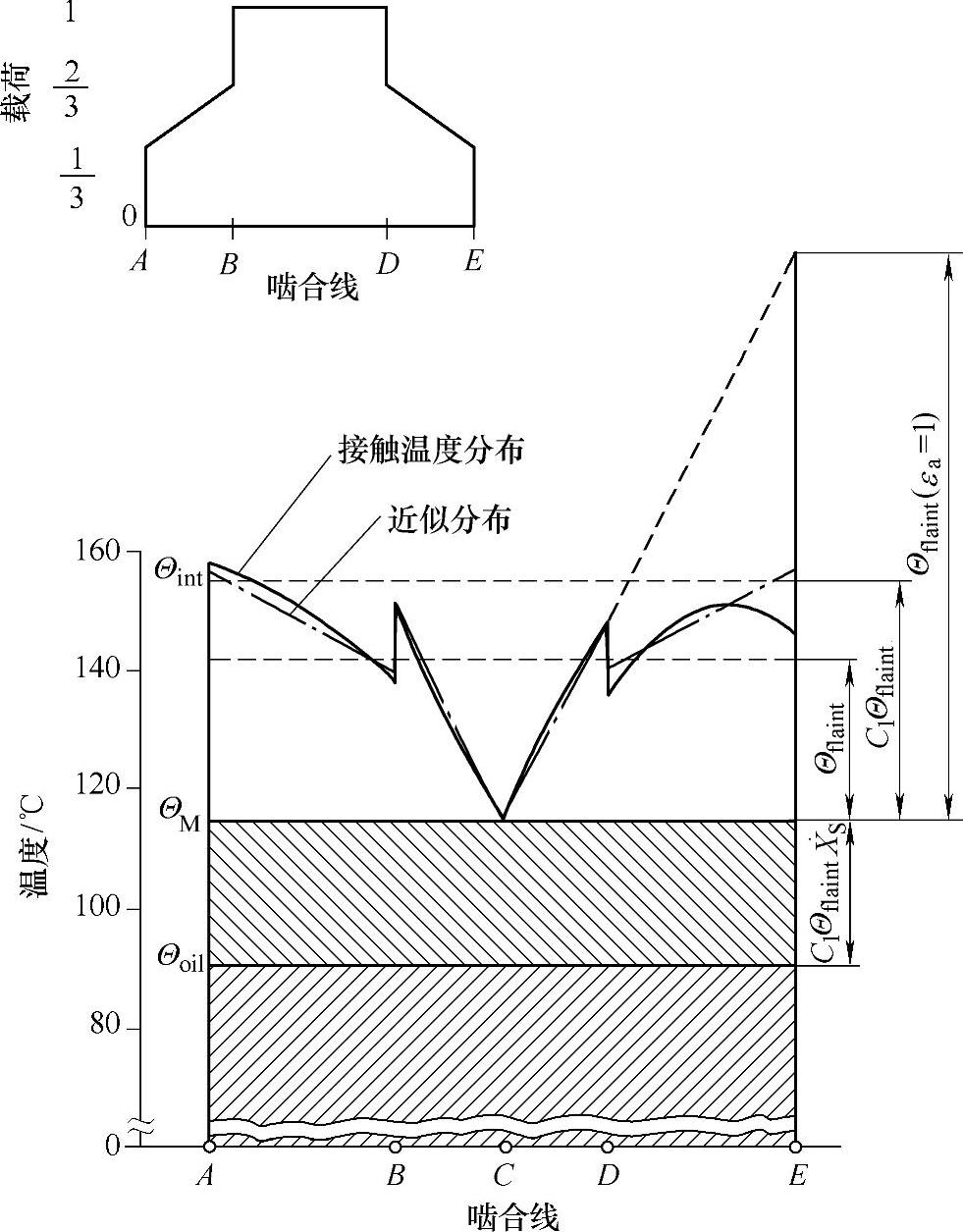
图6-1051≤εa<2时的载荷与温度分布
——在式(6-350)中:用Fmt代替Ft,beB代替b。
有效齿宽beB考虑了锥齿轮的鼓形。
beB=0.85b2 (6-392)
式中 b2——小轮与大轮的公用齿宽。
系数KA、KV、KBβ=KHβ以及KBα=KHα应按本章8.3.1节确定。
KBγ=1
⑤本体温度ΘM,见(3)1)⑤。
⑥平均摩擦因数μmc,见(2)1),并采用下列替换:
——在式(6-350)中:用Fmt代替Ft,beB代替b。
对于一般锥齿轮设计情况αt=αvt,即x1=x2:
ν∑C=2vmtsinαvt (6-393)
KBγ=1
⑦跑合系数XE,见(2)2)。
⑧热闪系数XM,见(2)3)。
⑨压力角系数Xαβ
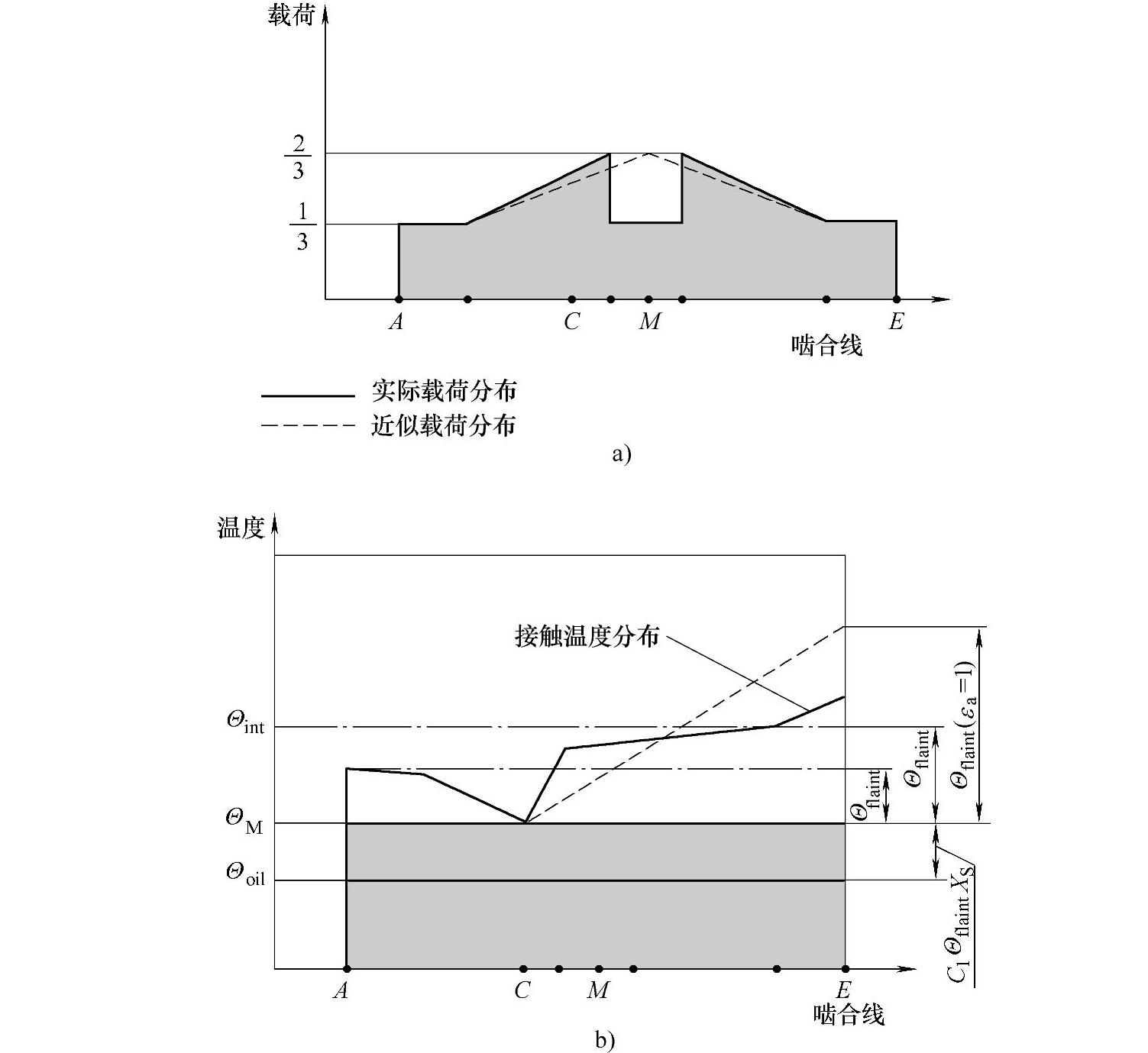
图6-106 2≤εa<3时的载荷与温度分布
a)沿啮合线的载荷分布 b)沿啮合线的温度分布
a.A法:系数Xαβ-A。对于一般锥齿轮设计的情况αt′=αvt,即x1=-x2:

b.B法:系数Xαβ-B,见(2)4)。
⑩ 小轮齿顶的几何系数XBE,见(3)1)⑩,并采用下列替换:
——在式(6-368)中:用uv代替u;
——在式(6-369)中:用dva1代替da1,dvb1代替db1;
——在式(6-370):αvt代替αt′。
⑾ 啮入系数XQ,见(3)1)⑾11,并采用下列替换:
——在式(6-374)~式(6-377)中:用εv1代替ε1,εv2代替ε2;
——在式(6-376)与式(6-377)中:用dva1,2代替da1,2,dvb1,2代替db1,2,αvt代替αt′,zv1,2代替z1,2。(https://www.daowen.com)
⑿ 齿顶修缘系数XCa,见(3)1)⑾21,并采用下列替换:
——在式(6-378)中:用εvmax代替εmax,εvmax是εv1或εv2中的最大值。
假定齿顶与齿根的修缘量被选为运行条件下的最佳值(满负荷接触斑点刚好扩展到齿顶而没有聚集现象),于是应用以下的近似方法:
Ca=Ceff和
⑬重合度系数Xε,见(3)1)⑾31,并在式(6-385)~式(6-391)中及其有效的条件下,采用下列替换:
用εva代替εa,εv1代替ε1,εv2代替ε2。
3)准双曲面齿轮 准双曲面齿轮胶合承载能力的计算方法是遵循圆柱齿轮积分温度准则的。
为计算胶合承载能力,将准双曲面齿轮当作具有与实际准双曲面齿轮同样滑动条件的当量交错轴斜齿轮来近似处理[见(3)3)⑾11当量交错轴斜齿轮副]。
①胶合承载能力计算的安全系数SintS,见(3)1)①。
②许用积分温度ΘintP,见(3)1)②。
③积分温度Θint,见(4)1)③并采用下列替换:
——在式(6-363)中:用C2H代替C2(按照试验结果,C2H=1.8),Θflainth代替Θflaint。
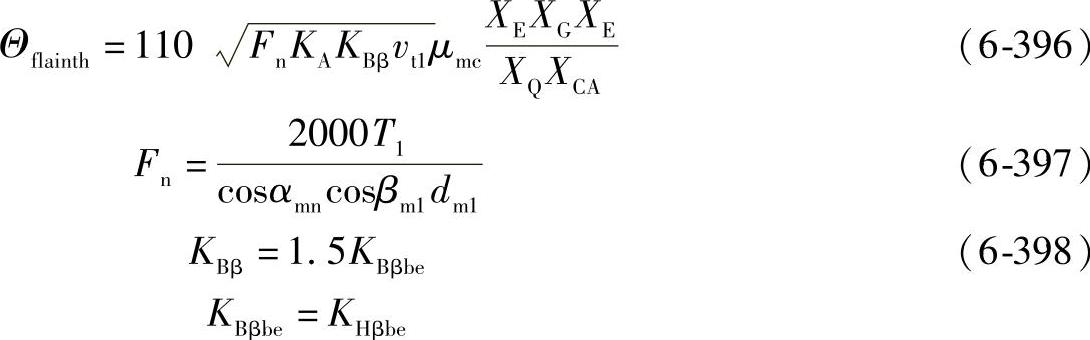
④本体温度ΘM,见(3)1)⑤。
⑤平均摩擦因数μmc,见(3)1),并采用下列替换:
——在式(6-346)中:用ρCn代替ρredC;
——在式(6-350)中:用beB/cosβb2代替b,Fn代替Ft;
beB见式(6-392)。
KBγ=1
KBγKBα=2.0(仅为计算μmc时的近似值) (6-399)
XR见式(6-353),并使用ρCn替代ρredC。
⑥跑合系数XE,见(3)2),并在式(6-354)中采用下列替换:
——用ρCn代替ρredC。
⑦几何系数XG。几何系数XG是考虑平均赫兹应力与沿啮合线的平均啮合长度影响的系数。作为一种近似方法,它可利用节点处的数值来确定(ρCn,L)。
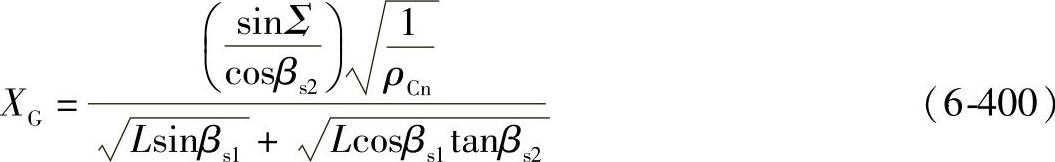

对于ξ与η的值,参见图6-107,或依据式(6-403)~式(6-406)确定。
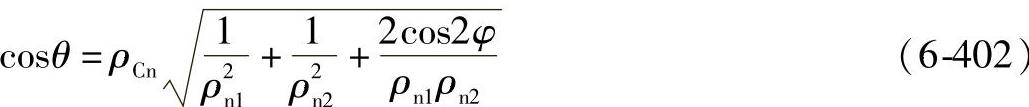
对于0≤cosθ<0.949
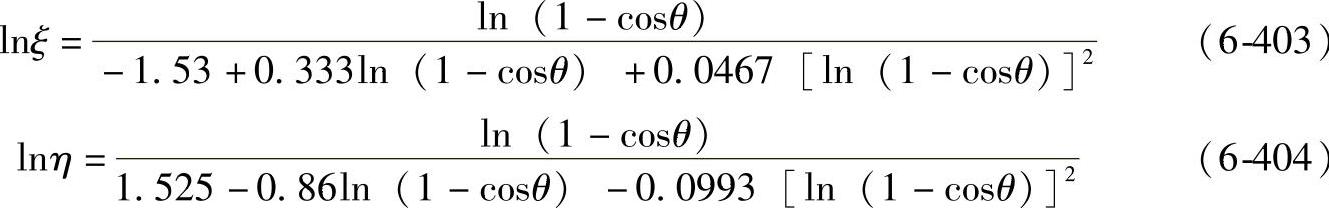
对于0.949≤cosθ<1
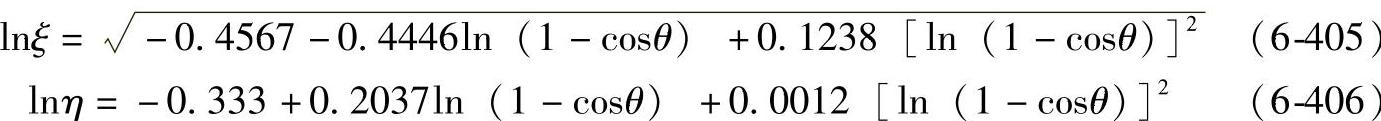
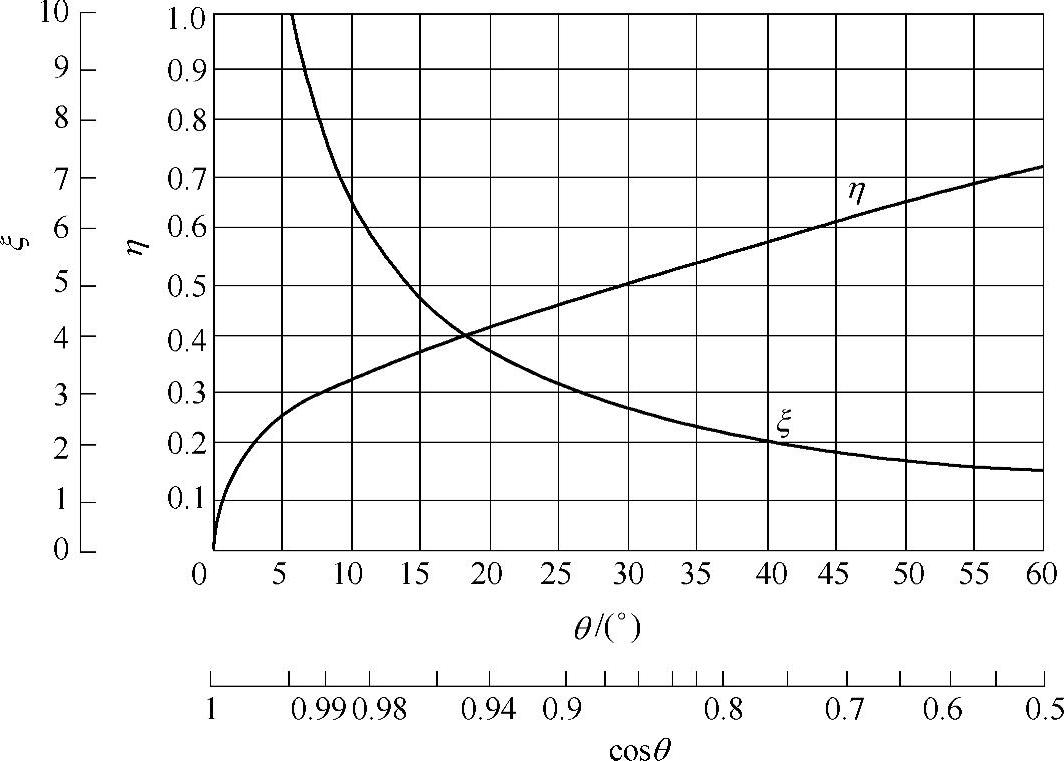
图6-107 作为cosθ的函数的辅助系数ξ与η
⑧ 啮入系数XQ,见(3)1)⑾11,并采用下列替换:
——在式(6-374)~式(6-377)中,用εn1代替ε1,εn2代替ε2。
⑨ 齿顶修缘系数XCa,见(3)1)⑾21,并采用下列替换:
——在式(6-378)中,用εnmax代替εmax,εnmax为εn1或εn2中的最大值。
为获得适当的齿顶与齿根的修缘:
Ca/Ceff=1,见(3)2)⑾21。
⑩ 重合度系数Xε
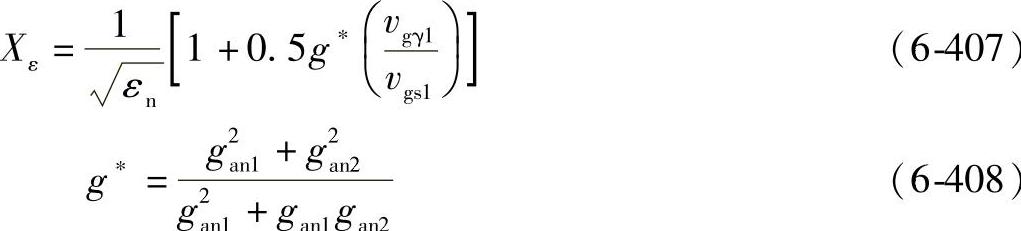
对于啮出线长度大致相同的(gan1≈gan2)齿轮副,滑动系数g接近等于1。
⑾11当量交错轴斜齿轮的计算。包含了准双曲面齿轮副转换成交错轴斜齿轮副的几何关系,将准双曲面齿轮的齿宽中点处的条件作为转换的基础(见图6-108)。
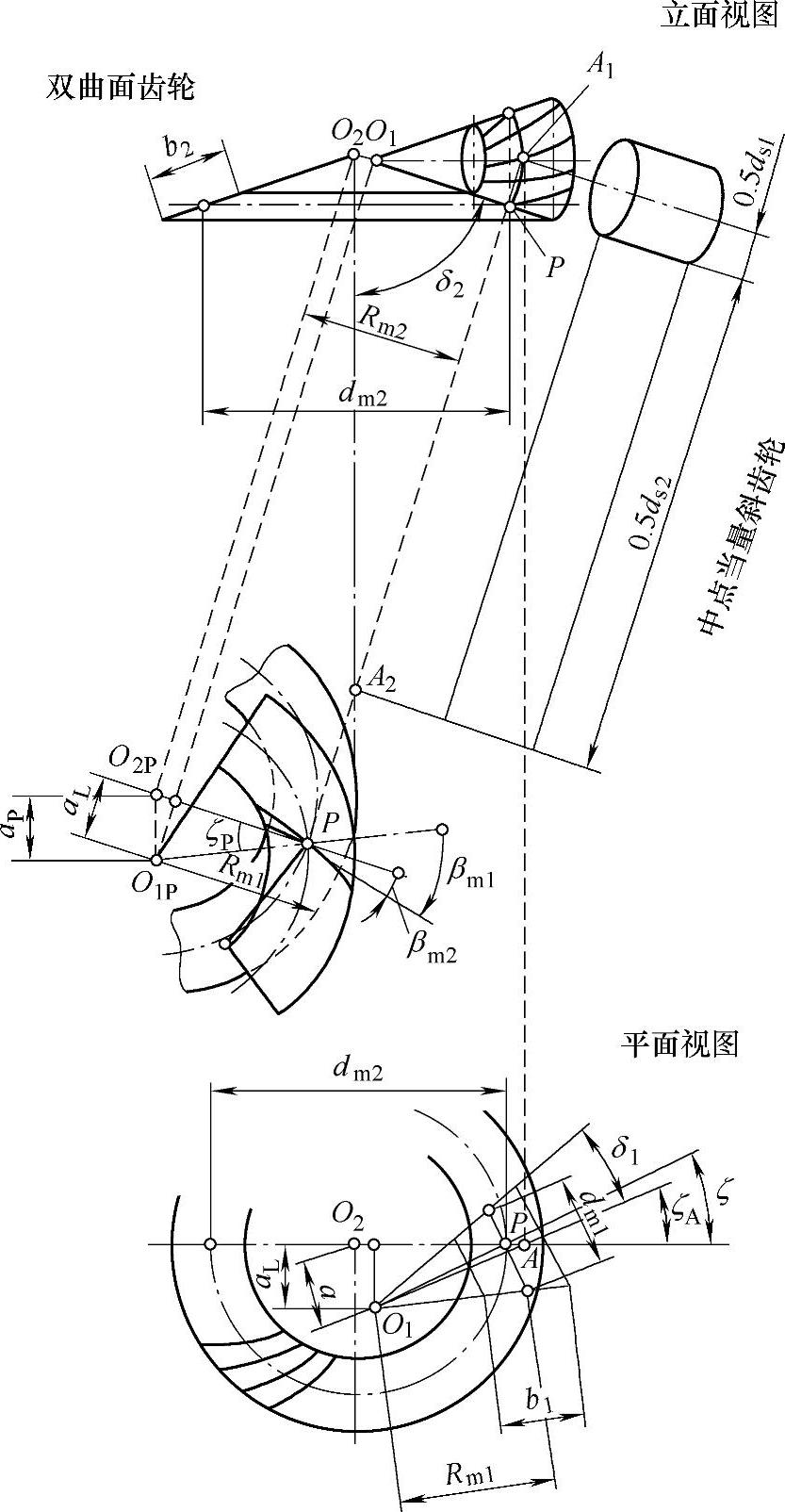
图6-108 当量交错轴斜齿轮的计算
当量交错轴斜齿轮的参数:
螺旋角
βs1,2=βm1,2 (6-409)
法向压力角
αsn=αmn (6-410)
交错轴斜齿轮的交错角
Σ=βm1-βm2 (6-411)
端面压力角αst1,2

基圆螺旋角βb1,2

分度圆直径

顶圆直径
da1,2=ds1,2+2ham1,2 (6-415)
基圆直径
db1,2=ds1,2cosαt1,2 (6-416)
交错轴斜齿轮的轴交角
tanβb1,2=tanβm1,2sinαmn (6-417)
φ=βb1+βb2 (6-418)
模数
msn=mmn (4-419)
法面基圆齿距
ρen=msnπcosαmn (6-420)
法截面上的曲率半径
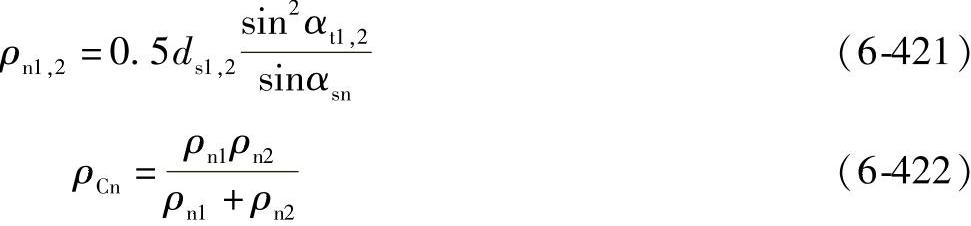
切线速度

节点处切线速度之和vΣC(βs1,βs2正值)
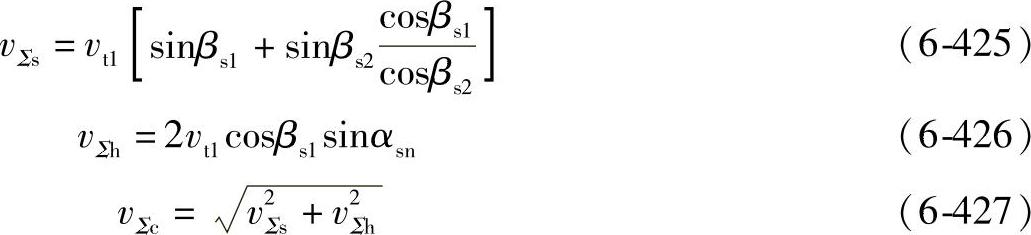
节点处滑动速度

小轮齿顶处最大滑动速度vgr1
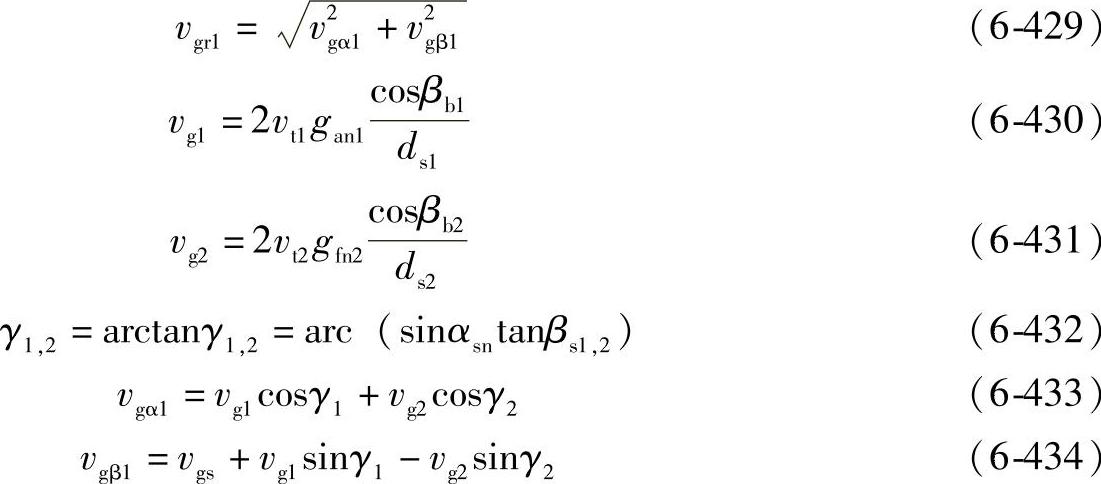
啮合线长度
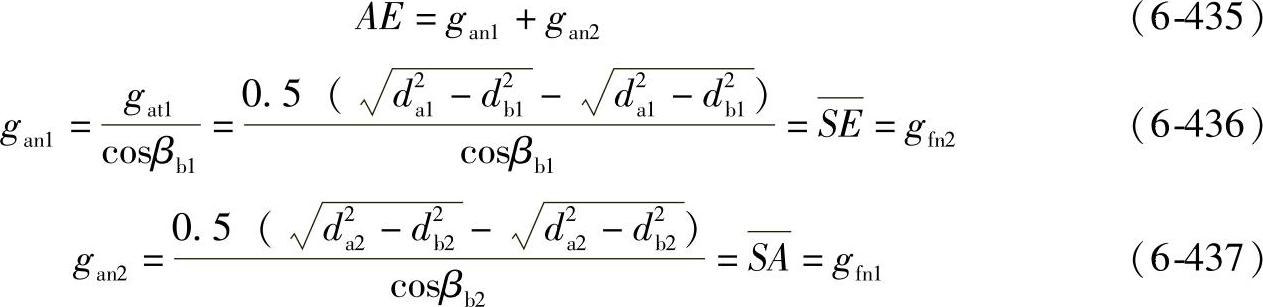
法截面内的重合度

4)胶合积分温度 胶合积分温度是产生胶合的温度极限值,它可以在试验结果的基础上进行计算。
此法适用于所有类型的油品(纯矿物油、EP油、合成油)。对于这些油的胶合承载能力已经通过试验齿轮确定(适用的试验例如有FZG-试验A/8.3/90、FZG L-42试验,Ryder齿轮油试验、或IAE齿轮油试验),或用实际的损伤情况来确定。
当试验齿轮的材料与相应的热处理与实际齿轮不一致时,必须修正胶合温度,因为极限温度是材料——油品系统的函数。
①胶合积分温度ΘintS。根据积分温度的设定,当平均齿轮温度超出称之为胶合积分温度的值时,齿轮有可能胶合,这个温度值假定为齿轮副的润滑油与齿轮材料的组合所特有的,而且是通过类似的润滑油与齿轮材料的组合试验来确定的。
胶合积分温度值可由将任何齿轮油的胶合,试验数据代入(3)1)、(3)2)、(3)3)中的公式得到。这样,胶合积分温度值对任一油品:纯粹的矿物油、EP油或合成油可以计算出来。
a.胶合积分温度的计算。热处理或表面处理齿轮钢与矿物油组合,组合的近似胶合积分温度值可从其他的热处理或表面处理齿轮钢和同样的润滑油组合的结果中得出。
ΘintS=ΘMT+XWrelTC2ΘflaintT(6-440)
式中,C2=1.5,由试验获得。
b.由试验结果确定ΘMT、ΘflaintT。图6-109所示为几种矿物油,在按照DIN 51354的FZG试验A/8.3/90、Ryder或FZG-Ryder试验以及FZG L-42试验等条件下确定的胶合承载能力的曲线。
为用计算机计算,图6-109~图6-111的曲线可以近似地用下列公式表达:
a)对于FZG试验A/8.3/90:
ΘMT=80+0.23T1TXL (6-441)
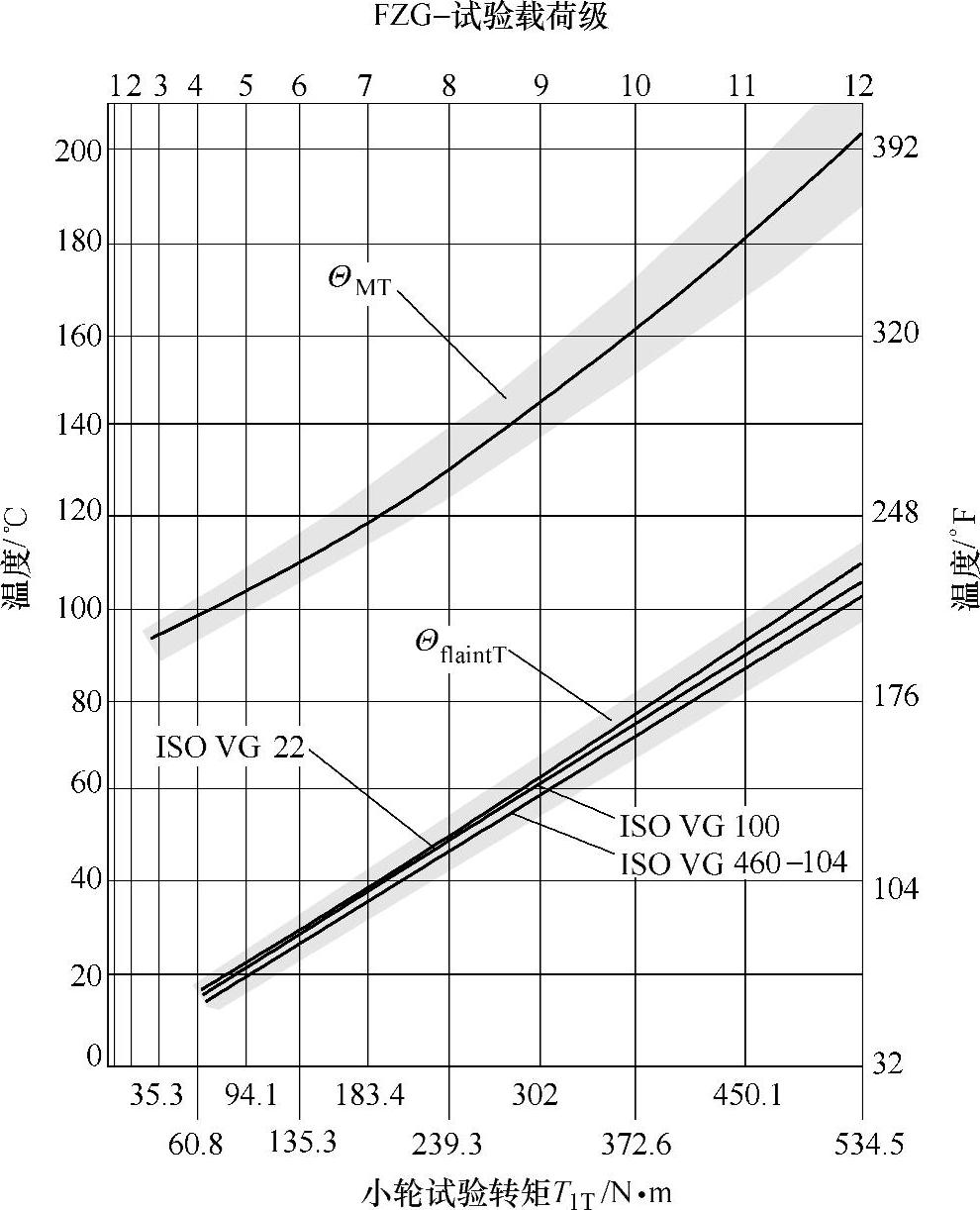
图6-109 FZG试验A/8.3/90的胶合温度ΘintS

T1T=3.726(FZG载荷级)2 (6-443)
b)对于Ryder与FZG-Ryder试验R/46.5/74:
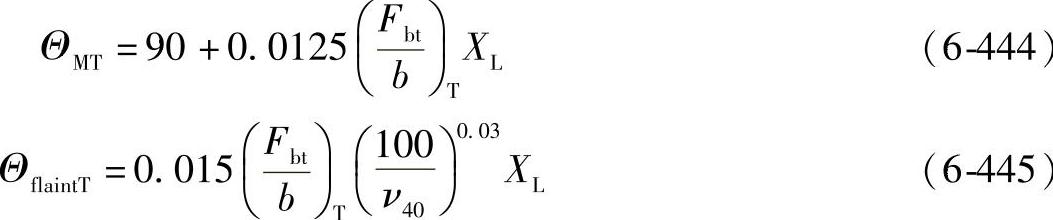
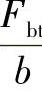
的单位为lb/in。
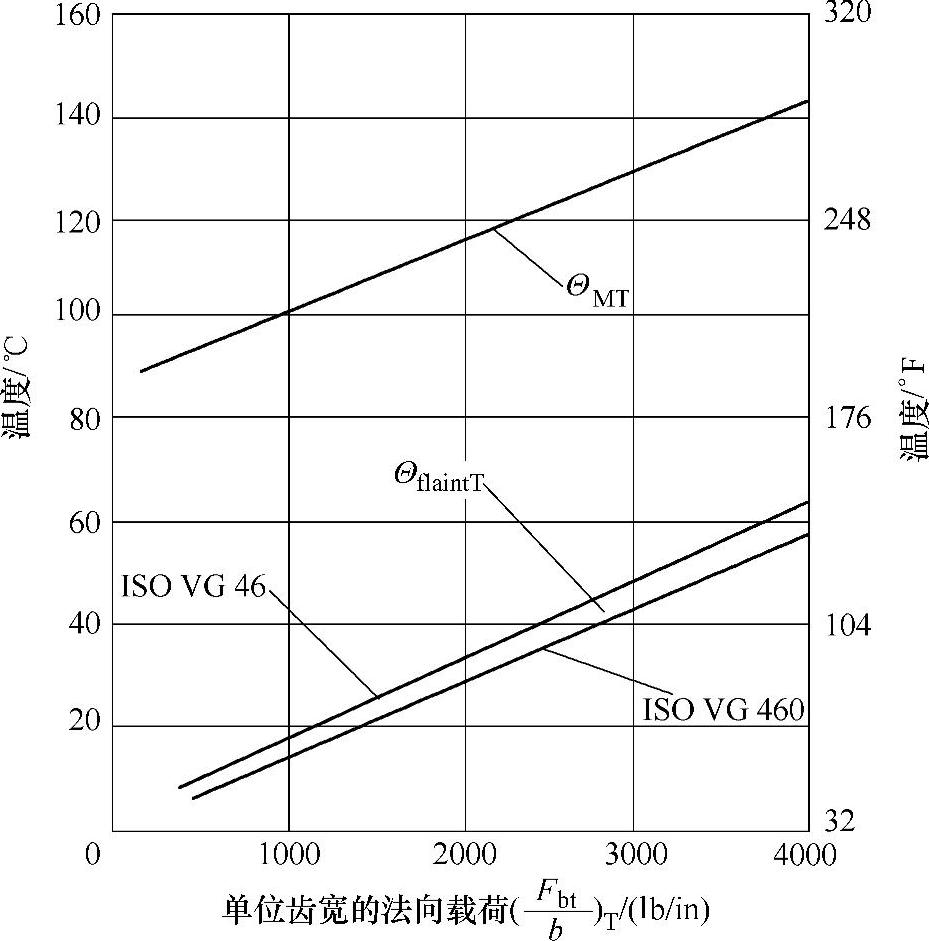
图6-110 Ryder与FZG-Ryder齿轮试验R/46.5/74的胶合温度ΘintS
c)对于FZG L-42试验141/19.5/110:
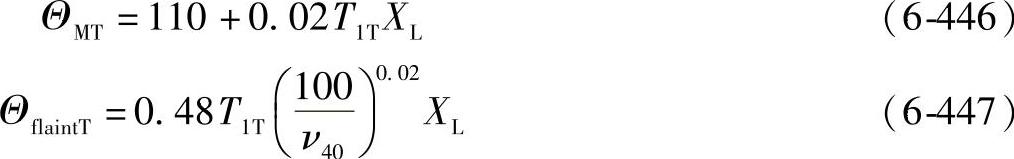
②相对焊合系数XWrelT。相对焊合系数XWrelT是考虑热处理或表面处理对胶合积分温度影响的一个经验性系数。

式中 XWT——试验齿轮的焊合系数,对于FZG齿轮试验、Ryder齿轮试验以及FZG L-42试验,XWT=1;
XW——实际齿轮材料的焊合系数,见表6-40。
(4)举例
为验证积分温度法的精确性,可用按照GB/Z 6413.2—2003方法对下面齿轮副的胶合承载能力进行计算。这些例子含有圆柱齿轮、锥齿轮以及准双曲面齿轮传动、中心距在a=22.07mm与a=2419.63mm之间,模数范围为m=1.25mm到m=20mm。被选用的齿轮箱中,有几台是因胶合失效而损坏的,或接近于胶合极限(边缘胶合)。在其他一些齿轮传动中没有观察到胶合失效。这些齿轮箱的参数与胶合计算的结果见表6-41~表6-49。
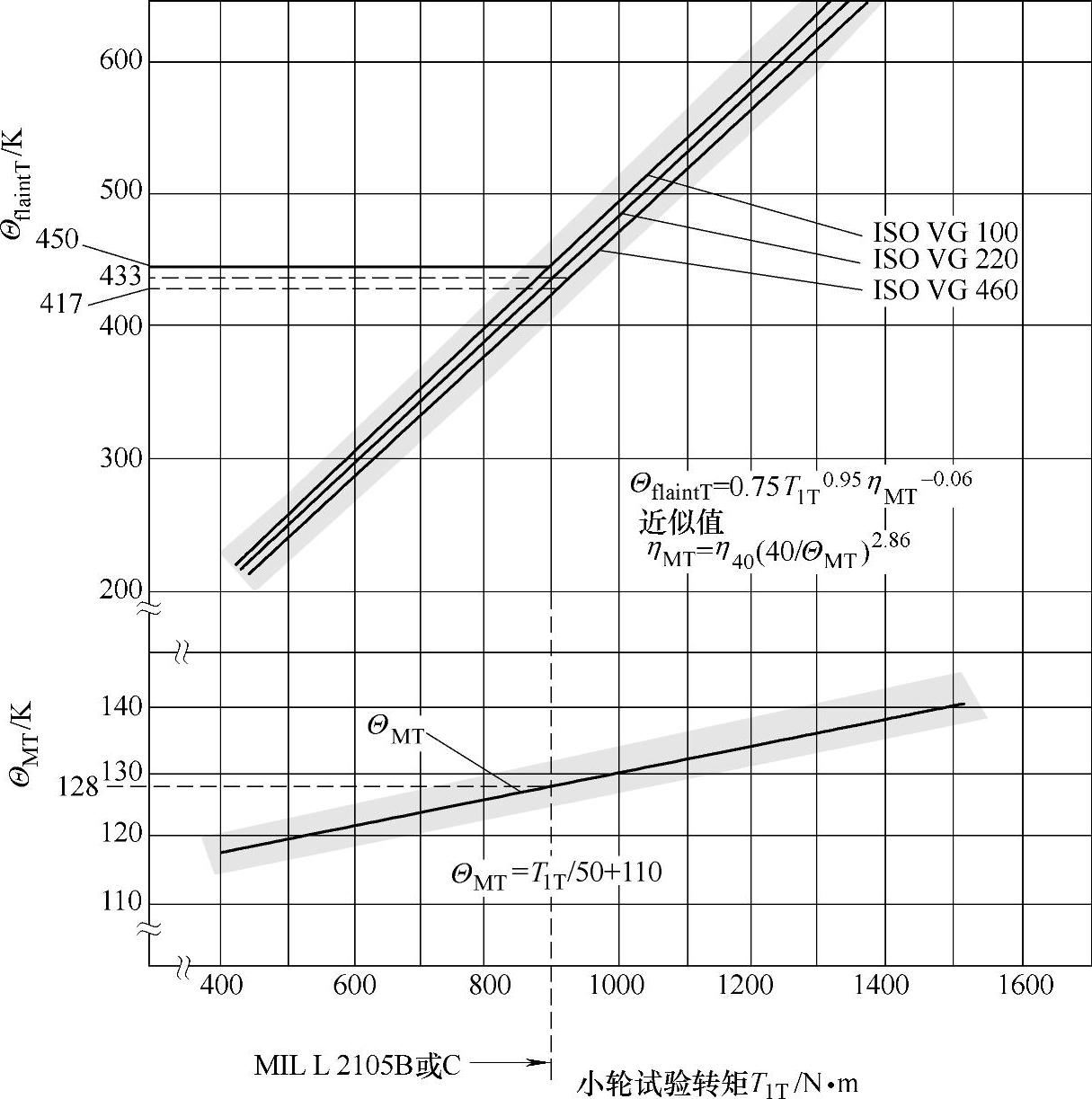
图6-111 FZG L-42试验141/19.5/110的胶合温度ΘintS
表6-40 焊合系数XW
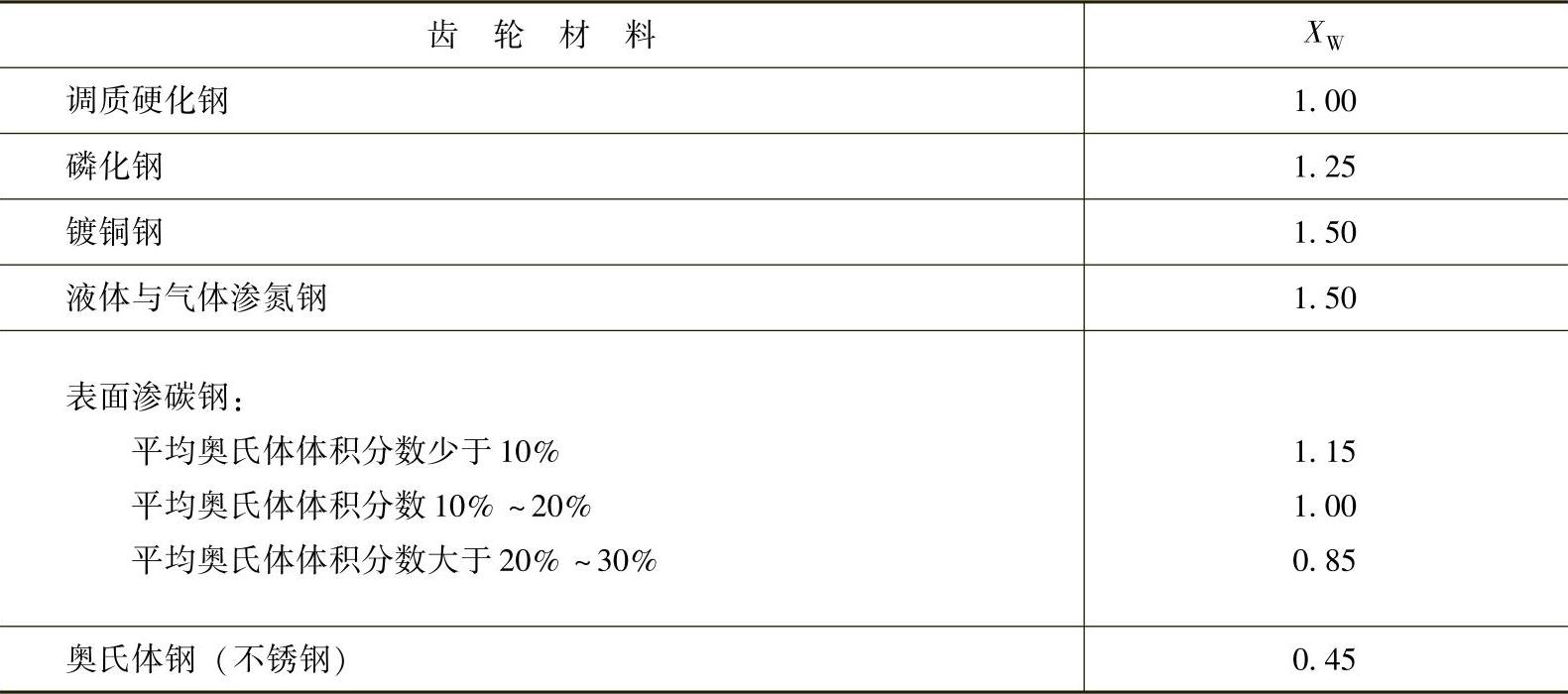
表6-41 斜齿轮:透平齿轮(来自迈克尔研究报告序号3)
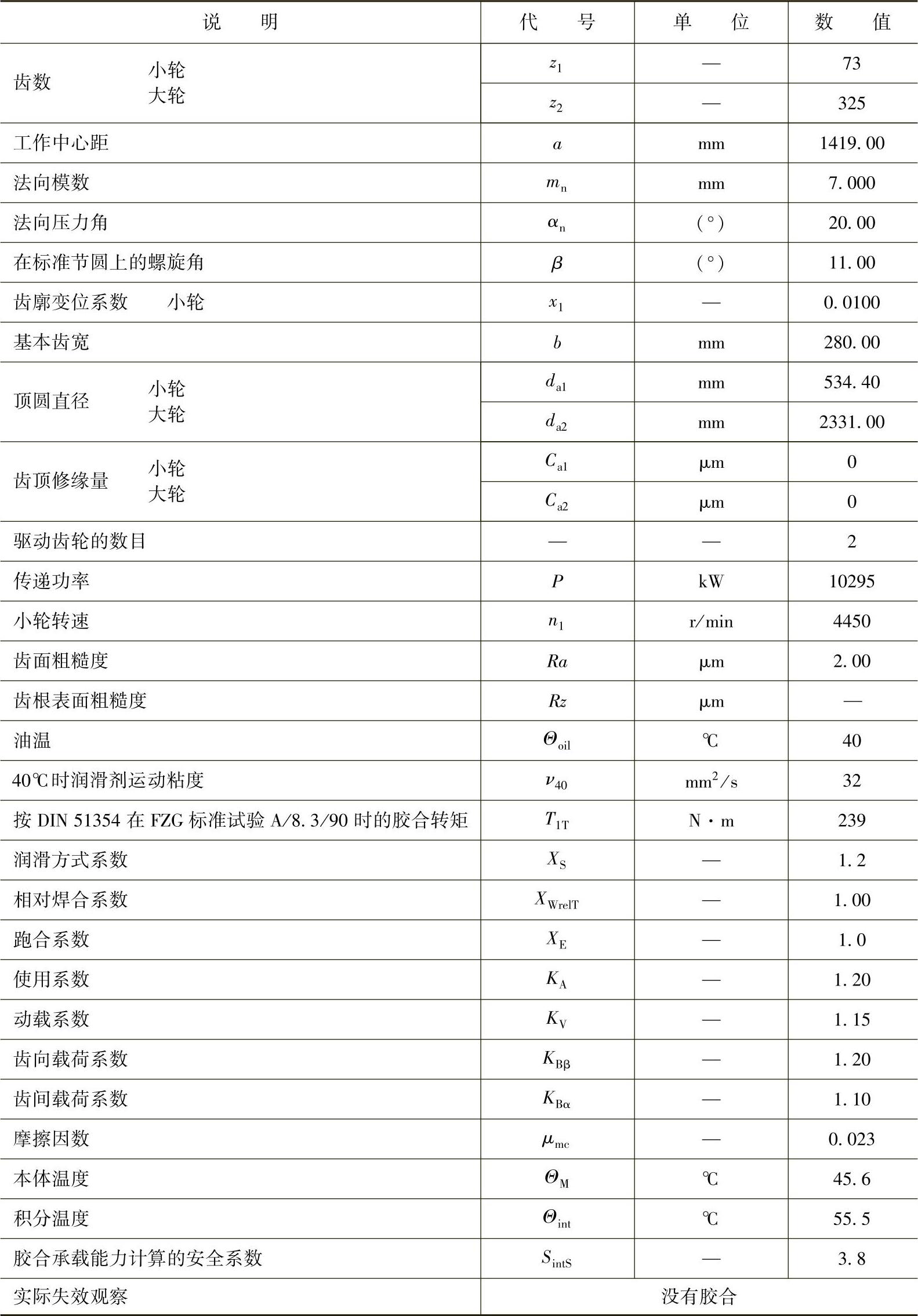
表6-42 斜齿轮:轧钢机齿轮(来自迈克尔研究报告序号5)
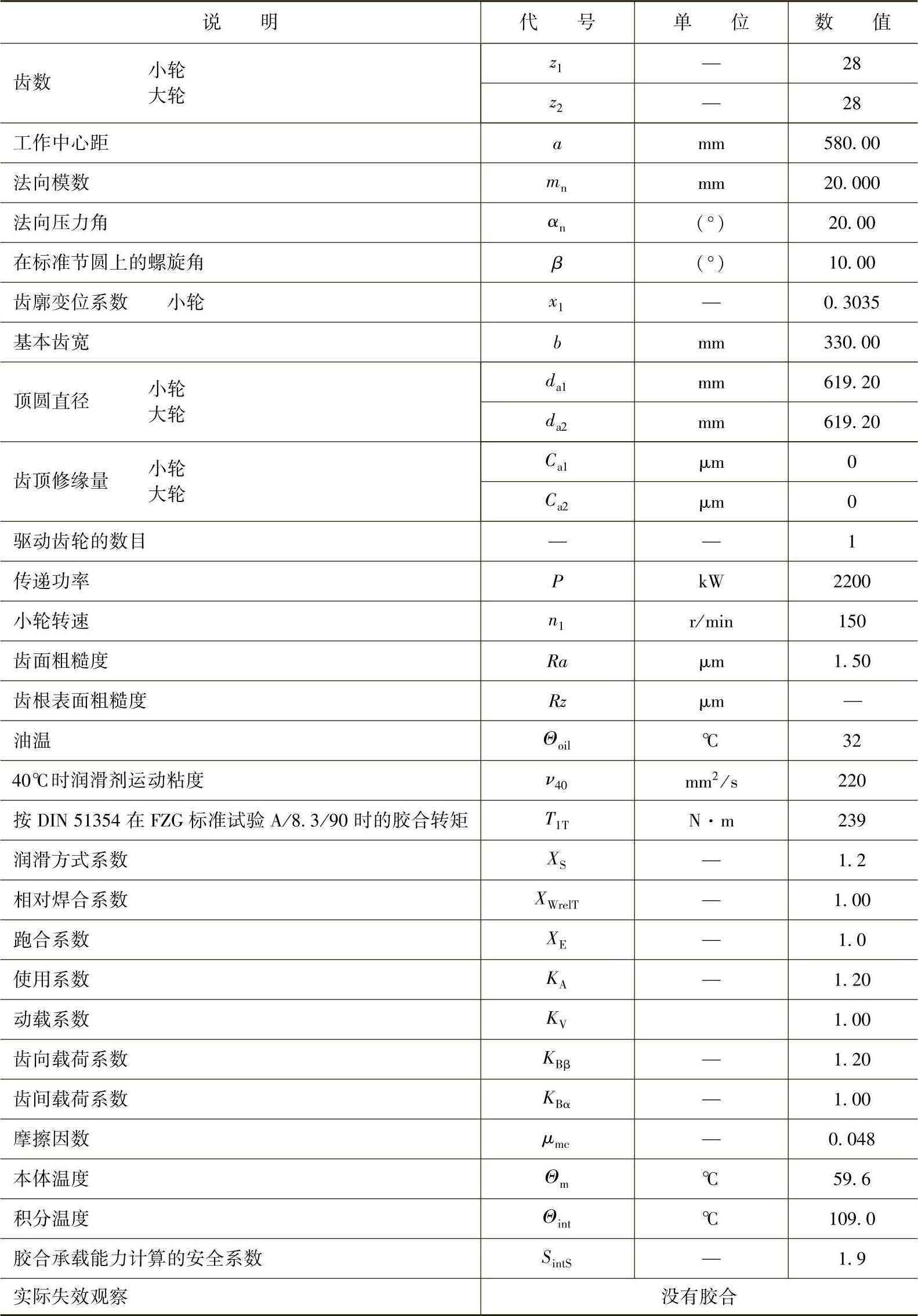
表6-43 斜齿轮:机床齿轮(来自迈克尔研究报告序号11)
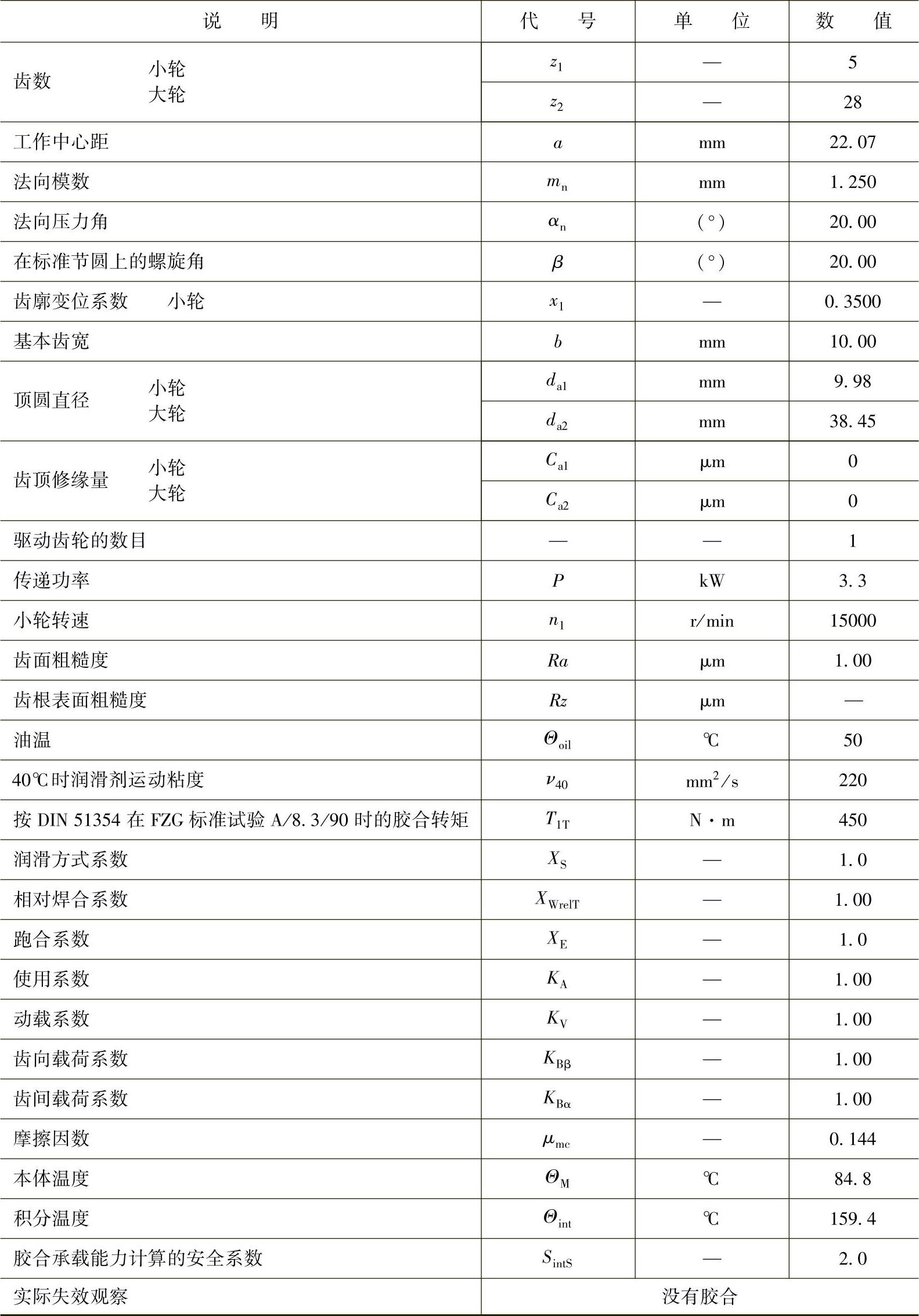
表6-44 斜齿轮:舰船齿轮(来自迈克尔研究报告序号13)
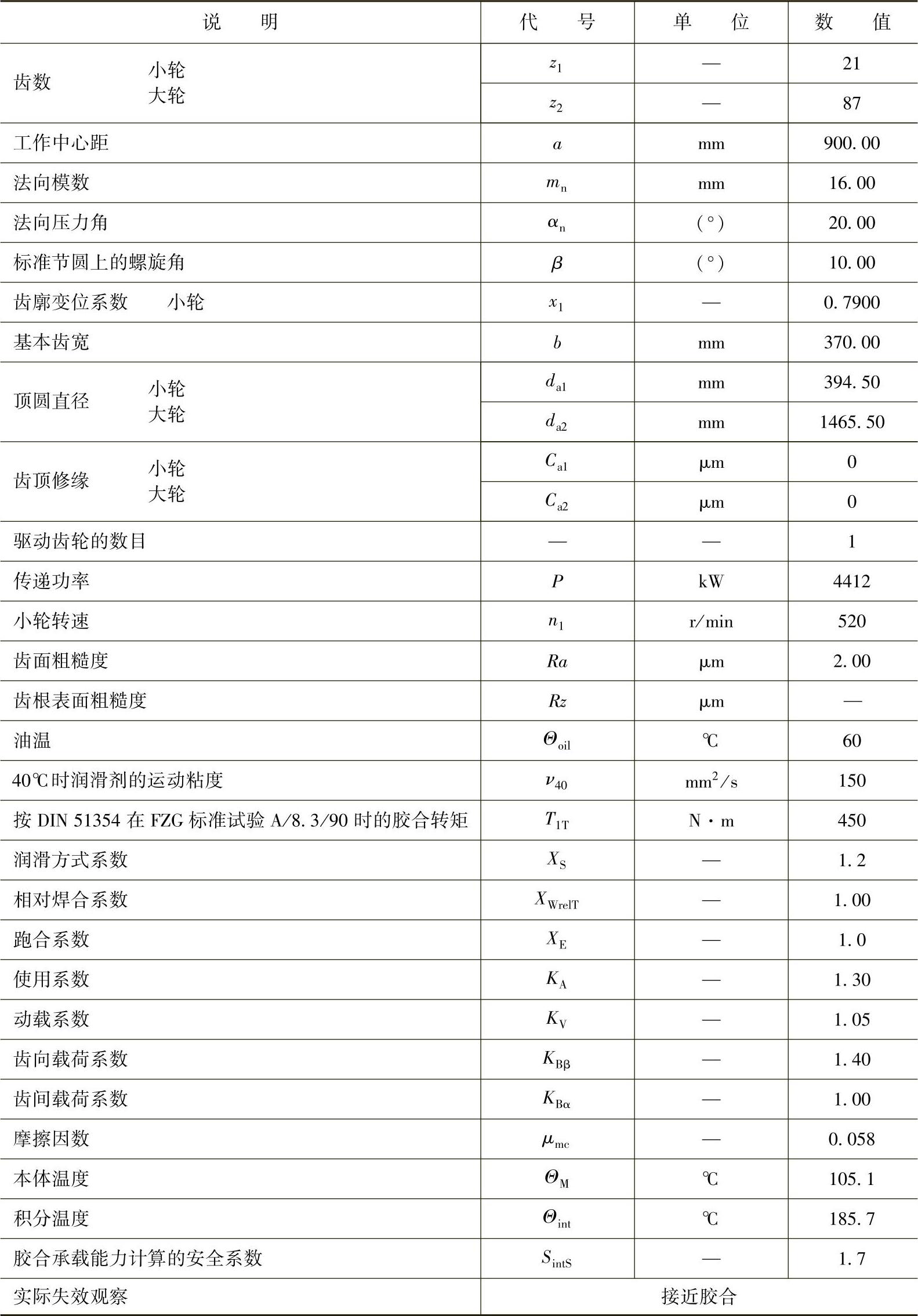
表6-45 斜齿轮:轧钢机齿轮(来自迈克尔研究报告序号16)
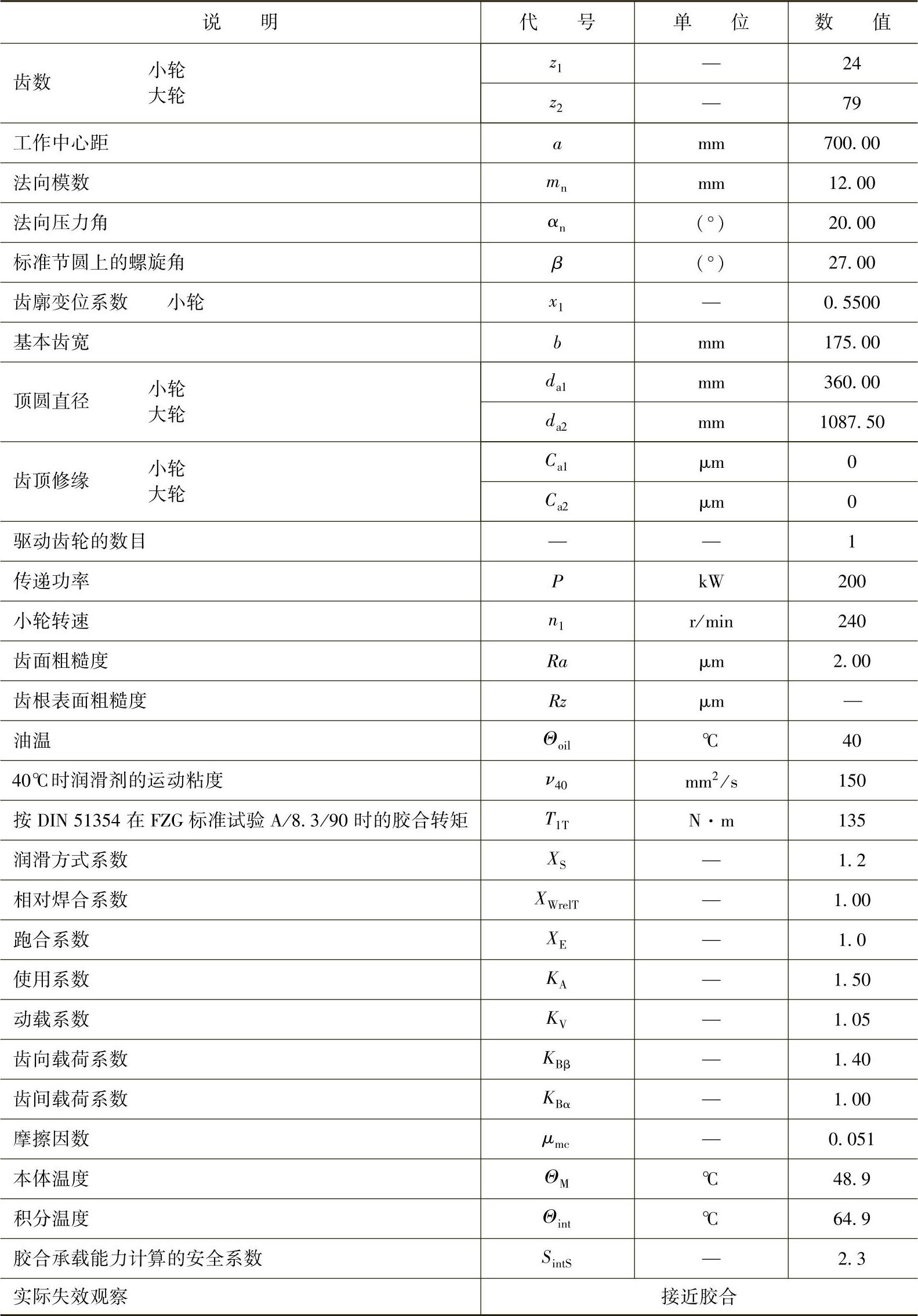
表6-46 斜齿轮:透平齿轮(来自迈克尔研究报告序号19)
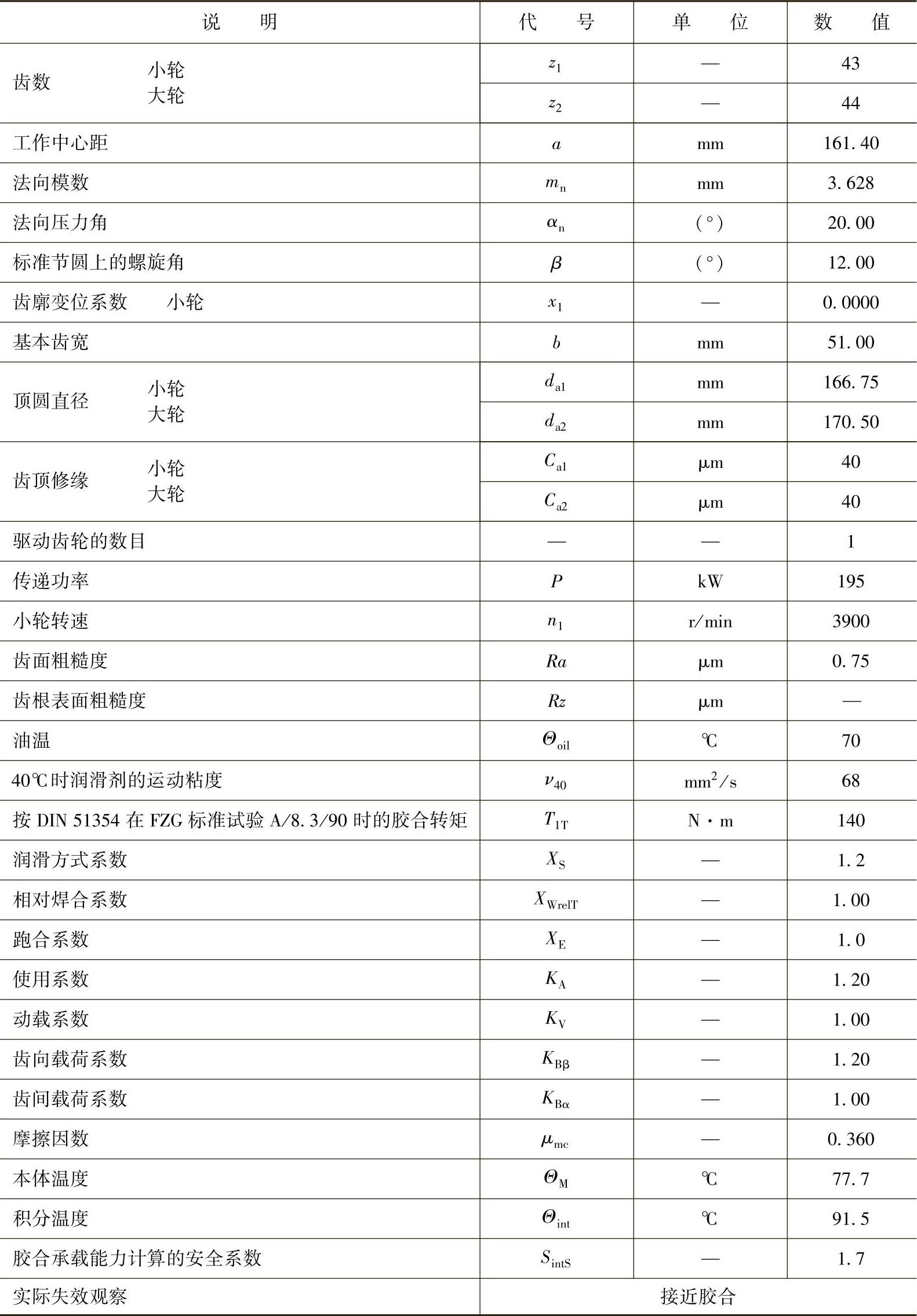
表6-47 斜齿轮:透平齿轮(来自迈克尔研究报告序号20)
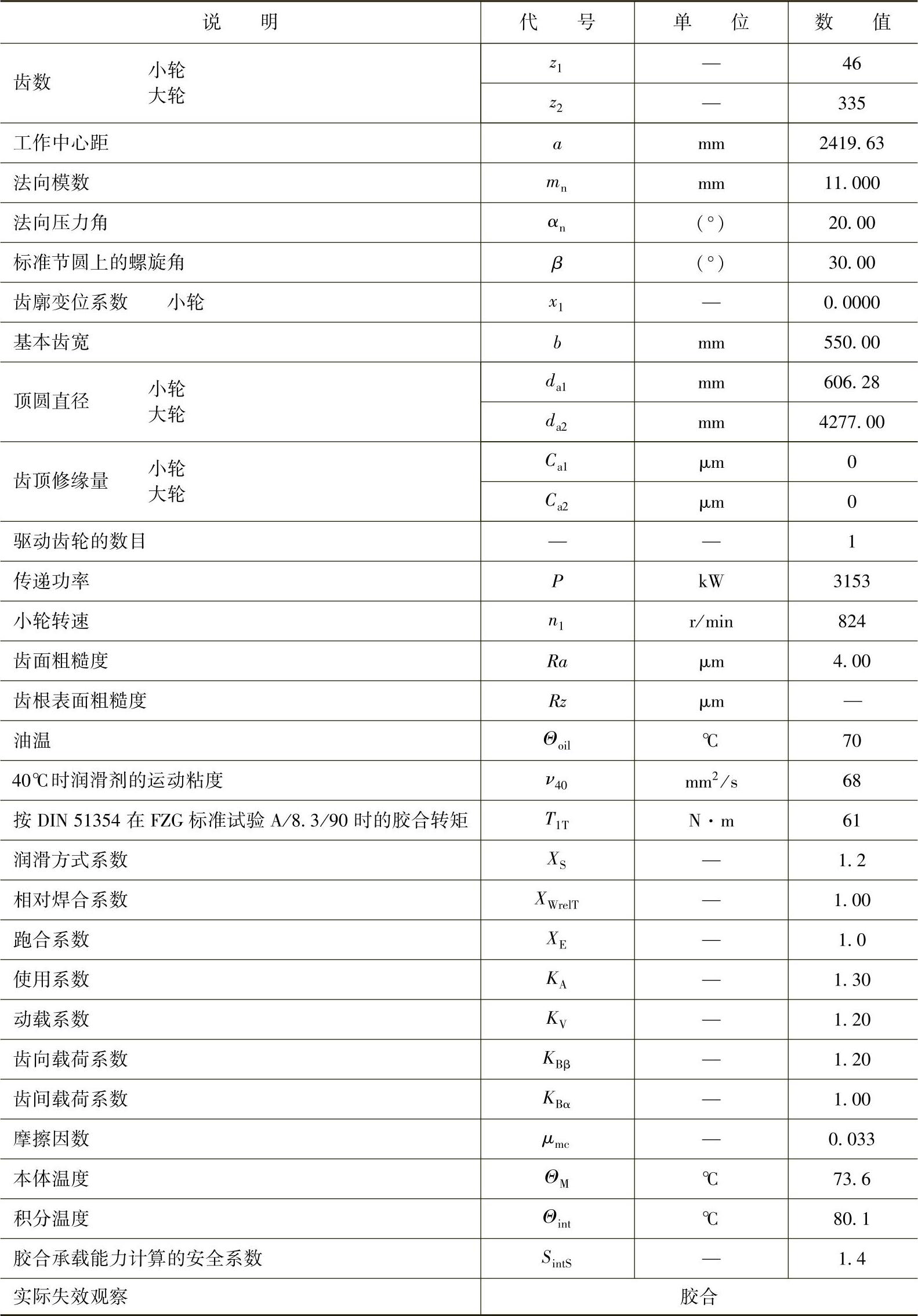
表6-48 直齿轮:车辆齿轮(来自迈克尔研究报告序号25)
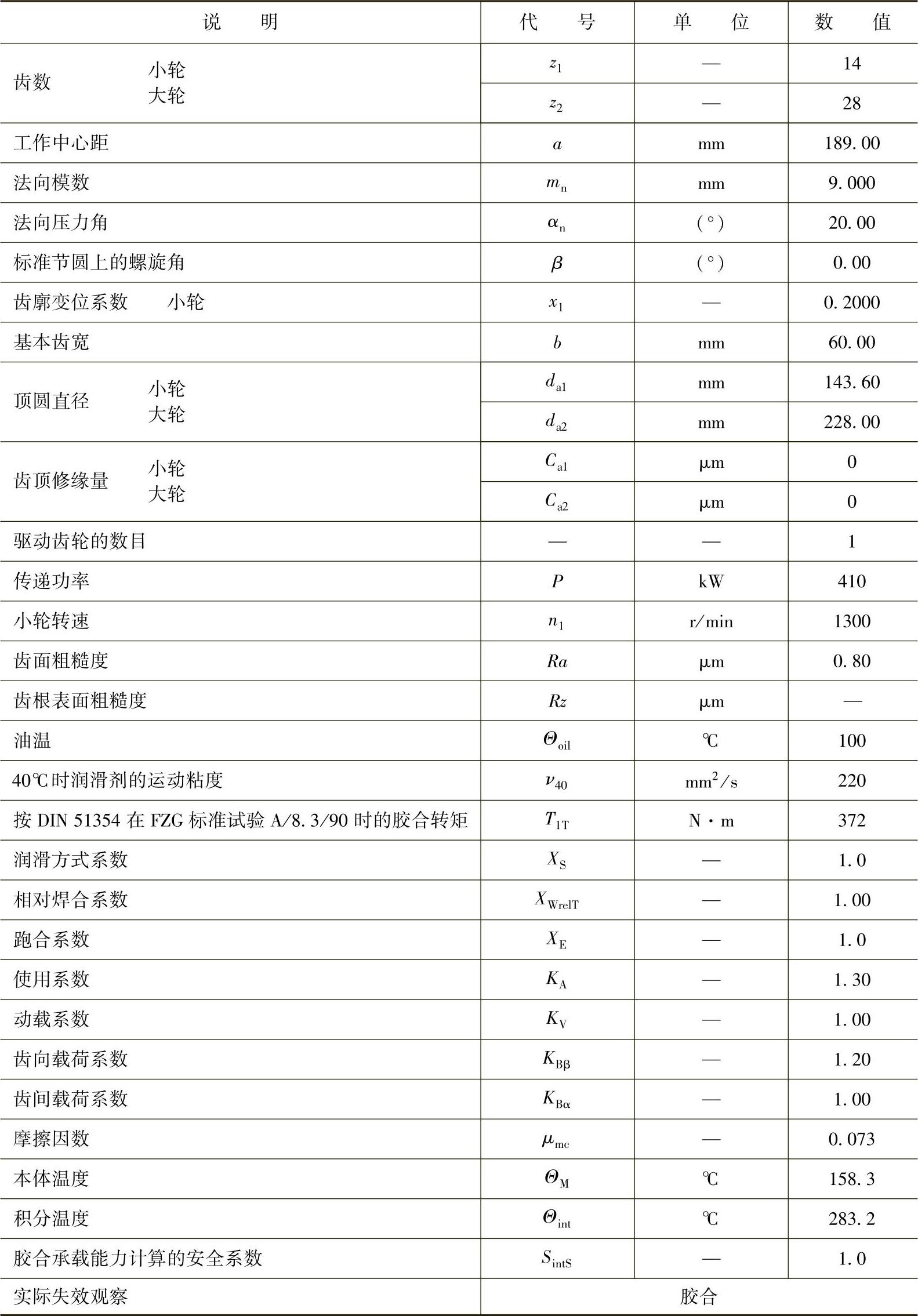
表6-49 锥齿轮与双曲面齿轮
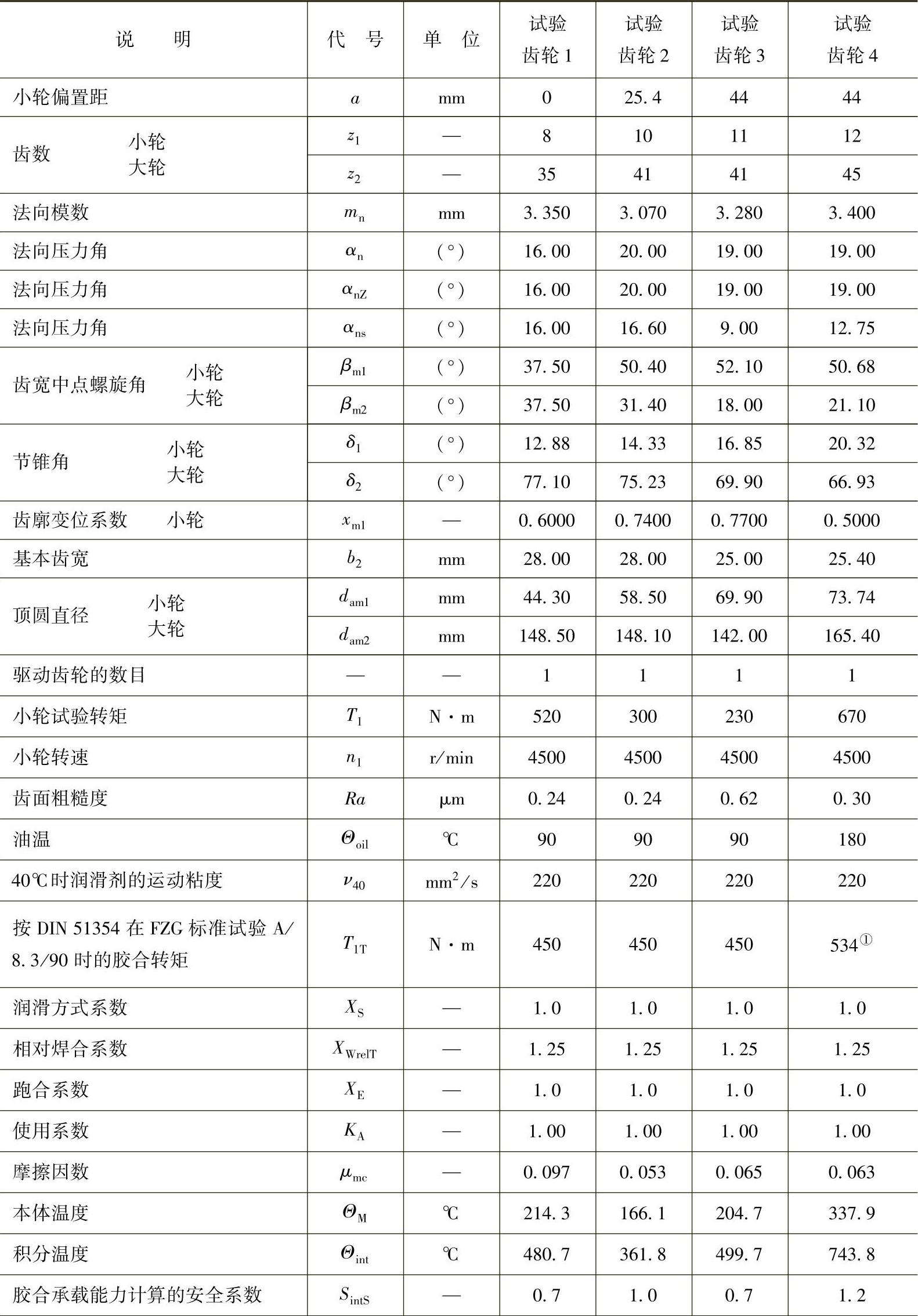
(续)

注:试验齿轮1、2与3取自:
Richter,M.:Der Verzahnungswirkungsgrad und die Fresstrag fähigkeit von Hypoid-und Schraubenradge-
trieben.Diss.T.u München(1976).
试验齿轮4是在胶合试验“FZG-Hypoidöltest Form A”中使用的。
①试验油品符合API GL-5规范。
(5)接触时间与胶合温度的相关性
本处叙述了关于CTC(接触时间规范)而使用一种可变胶合温度的方法。
不超过临界值的有效计算方法是:
——最大局部和瞬时总接触温度ΘS;
——接触的平均加权表面温度ΘintS。
假定这些限制与速度无关,这样,随着载荷达到最高速度而胶合载荷下降,故用EP润滑油的齿轮在高速时的计算是很保守的(图6-112)。
为了改善接近于基圆的接触点,在高速时的计算方法,必须考虑到临界温度ΘS取决于接触时间tC。图6-102给出了一个例子。计算曲线(a)是用两段直线(b)来近似的,CTC方法的这种修正给出了所要求的结果:计算的胶合载荷与测定的胶合载荷相吻合。
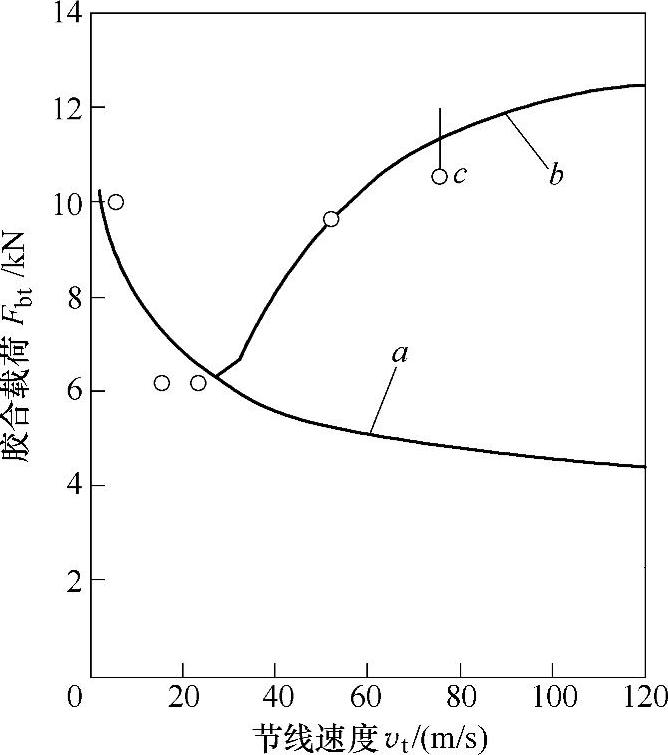
图6-112 胶合载荷与速度的关系
○—试验结果,A型齿轮,Z49油 a—曲线a:按图6-113的曲线c,用恒定的临界温度来计算 b—曲线b:按图6-113的曲线b,用与时间相关的临界温度计算 c—没有损伤
在图6-113中,用两段直线近似地表示了胶合温度ΘS与接触时间tC的关系: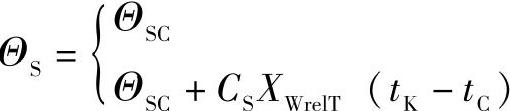
对于tC≥tK
对于tC<tK(6-449)
式中 ΘS——胶合温度;
ΘSC——在长接触时间时的恒定胶合温度,它相当于CTC的ΘS;
tC——接触时间;
tK——处于胶合-速度曲线的最小值时的接触时间;
CS——胶合温度梯度;
XWrelT——相对焊合系数。
CS与CK必须用短接触时间(高速)的两种油品试验来确定,试验中的接触时间应在20μs的范围内。
tC与tS的计算如下(用符号表明试验在低速、中速以及高速下进行):

胶合温度存在一个恒定的值(在长接触时间的范围内)
ΘSC=Θl (6-452)
tC是齿面(小轮或大轮)上的一个点通过赫兹接触宽度(2bH)所必需的时间
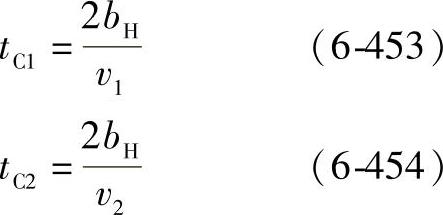
tC=min(tC1,tC2) (6-455)
式中 v1、v2——小轮和大轮的齿面速度。
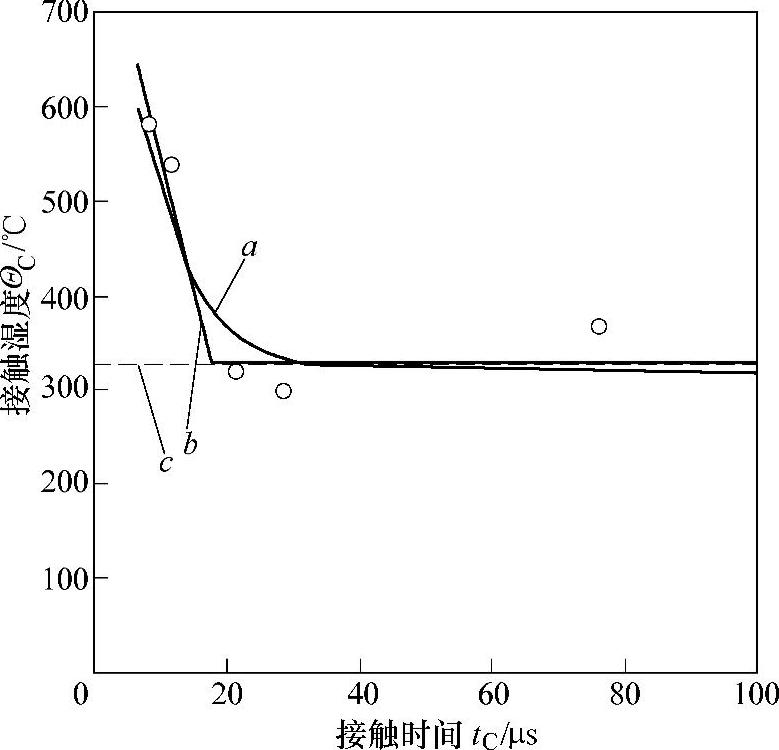
图6-113 接触时间tC对临界接触温度的影响
○—试验结果,A型齿轮,Z49油 a—曲线a:计算的临界温度 b—曲线b:曲线a的近似直线 c—曲线c:临界温度
如果没有适用于高速时的油品试验结果,胶合温度ΘS可用下列推荐的办法获得近似值:
1)非EP油 高速时临界温度的提高是非常少的,所以用恒定的胶合温度ΘSC来计算。
2)EP油 建议用下面的tK与CS值:
tK=18μs
CS=18K/μs
对于胶合温度ΘS,其公式为
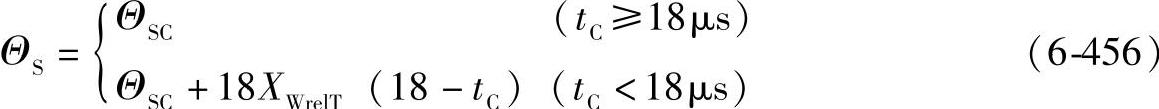
ΘSC必须在胶合油品试验中确定,例如按照DIN 51354的FZG试验A/8.3/90。
圆柱齿轮切线速度与赫兹接触宽度的确定:
齿面上的切线速度:

赫兹接触宽度(小轮与大轮弹性模量相同,线接触):

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






