（1）范围

本部分根据布洛克接触温度的概念规定了评价胶合危险的方法和公式。

布洛克的基本概念应用于具有移动接触区的所有机械零件。闪温公式对于带状或近似带状的赫兹接触区与足够高的佩克莱特（Peclet）数为特征的工作条件下是有效的。

（2）胶合和磨损

1）胶合和磨损的产生 当齿轮轮齿完全被润滑油膜分开时，两齿面的凹凸不平之间是不接触的，通常不存在胶合和磨损，此时的摩擦因数相当小。在油膜较厚时，由于突然的热不稳定性引起的类似胶合损伤的这种特殊情况不在此讨论。

当弹性流体动力油膜较薄时，齿面凸凹之间偶尔会直接接触，随着平均油膜厚度的减薄，直接接触的次数相应增加，则可能会产生磨料磨损、粘着磨损或胶合。由于齿轮轮齿的滚动作用或润滑油中含有磨粒会引起磨料磨损。粘着磨损是由先局部焊合，随即分离，从而导致一个或两个啮合轮齿上的材料微粒转移而引起的。如果磨粒磨损或粘着磨损是轻微的，且随着时间的推移而减轻，作为一种正常跑合过程则对轮齿不会造成危害。

与轻微磨损不同，胶合是能导致轮齿扩展性损伤的粘着磨损的严重形式。与具有明显发展期的点蚀和疲劳折断不同，瞬时过载会导致胶合失效。

润滑油中过分进气或存在污染，诸如悬浮的金属颗粒或水，也会增加胶合的危险。高速齿轮胶合后，由于振动而引起更大的动载荷，振动通常会导致进一步的胶合、点蚀、断齿损伤。

在大多数情况下，使用具有增强抗胶合添加剂^[3]的润滑油能提高齿轮抗胶合承载能力。然而，重要的一点是要意识到使用抗胶合添加剂的一些不足之处：使铜腐蚀、弹性材料的脆化，以及缺乏全球通用性等。

本方法不适用于评价冷胶合，冷胶合通常在低速（节圆线速度小于4m/s）、质量很差的调质重载齿轮上产生。

2）转换图 在使用液体润滑油润滑的运行条件下，较严重的钢接触滑动的润滑状况可用转换图描述。图6-82所示的转换图适用于恒定油浴温度下的接触运行。

当法向力F_n和相对滑动速度v_g同时落在A1-S线以下，即图6-82的Ⅰ区时，润滑状况的特征可用摩擦因数大约为0.1、单位磨损率（即：每单位法向力、每单位滑动距离下的体积磨损量）为10^-2～10^-6mm³/（N·m）来表达。

当v_g不大于S点的值，且载荷增加进入Ⅱ区时，则转换进入第二种润滑状况。这种轻微磨损润滑条件的特征可用摩擦因数为0.3～0.4、单位磨损率为1～5mm³/（N·m）来表达。

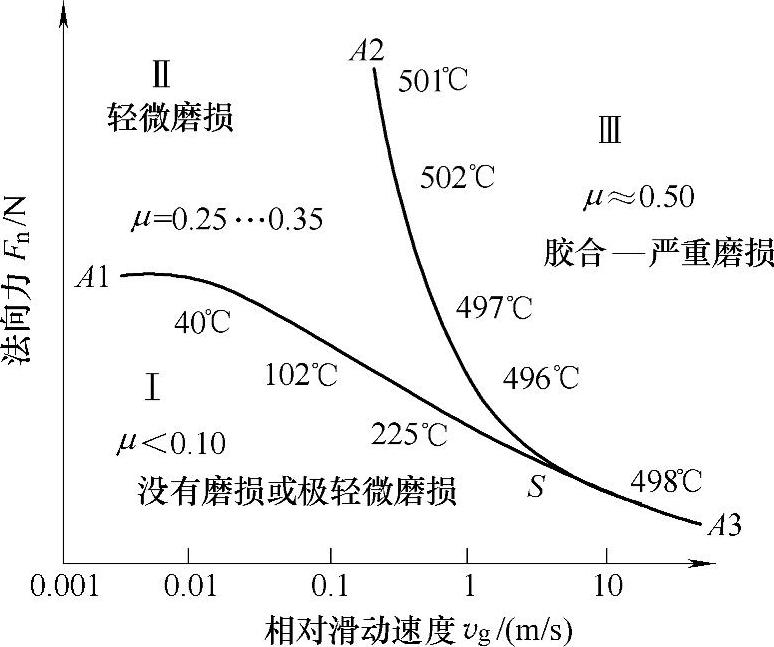
图6-82 具有计算接触温度实例的逆向形状转换图

如果载荷进一步增加，则转换进入第三种润滑状况，即进入以A2-S为边界线的Ⅲ区。这个区域的特征可用摩擦因数等于0.4～0.5来表达，然而，与Ⅰ区和Ⅱ区相比磨损率相当高，从100～1000mm³/（N·m）。磨损表面呈现胶合形式的严重磨损。当相对滑动速度超过S点后，如果载荷增加，则直接从Ⅰ区转换到Ⅲ区。

有足够的证据证明A1-S-A3线的位置取决于润滑油粘度及赫兹接触压力。当F_n和v_g同时落在此线以下时，则认为，齿面由一层较薄的润滑油膜分隔开，但此膜被粗糙的凸凹部分所穿透。对于这种情况，称为“边界弹流动力润滑”。

在Ⅲ区中，液体油膜完全失去了作用，这个区域即为“初始胶合”区域。有证据表明以A2-S线为边界发生的转换与接触温度达到临界值相关。这就是布洛克的基本概念。

给出的这个转换图适用于新的组件（即未氧化钢的接触），如齿轮、凸轮及从动件等。这个转换图符合四球试验及柱—环试验的结果。

沿A1-S-A3曲线的温度范围（从油池温度开始，依次为整个本体温度，接触面本体温度）：在v_g=0.001m/s时为28℃到v_g=10m/s时的接触温度为498℃。这个温度特性充分表明在恒定的接触或接触面本体温度下，（边界）弹流动力润滑未被破坏，例如与化学吸附性材料的软化有关。相反，随着滑动速度的增加承载能力的明显降低则认为是由于润滑油粘度的降低。

与上述情况不同，沿曲线A2-S-A3的计算接触温度则趋向于一个恒定的值，即用GCr15钢时大约为500℃，见图6-82。这表明从Ⅱ区到Ⅲ区的转换与用钢的不同有关，从轻微粘着到严重粘着，引起了表面磨损机理的变化，也许还包括热弹不稳性机理。

因此，结果表明胶合与接触温度的临界值有关。对于钢，用矿物油润滑时，临界值大约为500℃，它并不取决于载荷、速度和几何参数。

3）初始胶合时的摩擦 在图6-82所示的转换图中，胶合时，摩擦因数从0.25跳跃到0.5。相应的接触温度大约为500℃。这个接触温度是测量的接触面的本体温度28℃与计算的闪温470℃的和。

在计算闪温时所用的摩擦因数是刚要转换前的摩擦因数，即μ=0.35。如果这种方法不仅要用于柱与环实验而且还要用于齿轮传动（在设计阶段）时，在计算中接触温度的临界值和摩擦因数值的选取应协商一致。

齿轮承载能力可以预估：

——当使用摩擦因数μ=0.5时，偏于安全；

——根据润滑油的不同，所使用的摩擦因数为μ=0.25～μ=0.35时，较精确；

——根据以前的经验，在稳定的工作条件下，所用的摩擦因数较低，那么限定的接触温度相应地也较低。

根据经验，对于不加和加少量添加剂的矿物油，油和滚动材料的每一种组合有一个临界胶合温度。通常，这个温度是恒定的，与运行条件、载荷、速度和几何参数无关。

对于加大量添加剂的矿物油和一些种类的复合油，临界胶合温度随着装置运行条件变化而变化。因此，此时的临界温度必须由模拟齿轮装置运行条件的实验分别确定。

（3）基本公式

1）接触温度 接触温度是接触面的本体温度Θ_Mi和闪温Θ_fl之和。

Θ_B=Θ_Mi+Θ_fl （6-222）

闪温温度沿接触轨迹的变化见图6-83。

最大接触温度为

Θ_Hmax=Θ_Mi+Θ_flmax （6-223）

式中 Θ_flmax——Θ_fl的最大值，它不是位于啮入轨迹上就是位于啮出轨迹上。

胶合的可能性可通过计算最大接触温度和其临界值的比较进行预测。接触温度的临界值可通过齿轮胶合试验确定，或通过使用现场的调查研究确定。

对于胶合危险性的可靠评价，重要的是在分析中，要使用齿轮本体温度的精确值。

2）闪温公式 对于（近似）带状接触区和不同方向的切向速度（如准双曲面齿轮），布洛克闪温公式最常用的表达式为

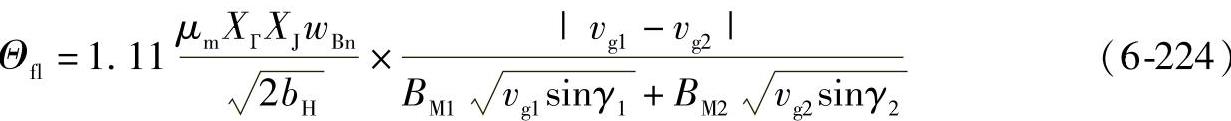
对于具有带状接触区和切向速度平行的圆柱齿轮和锥齿轮，常用的表达式为

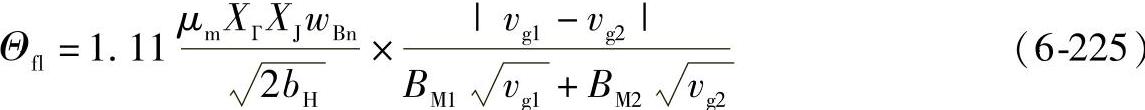
或用等效表达式：

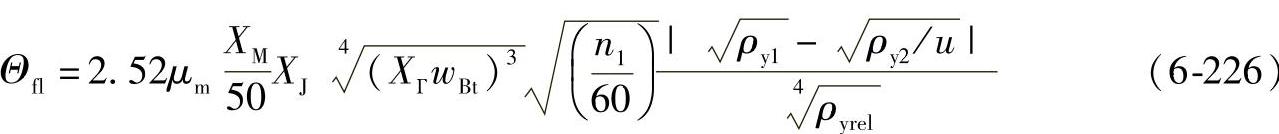
式中 μ_m——平均摩擦因数；

X_M——热弹系数，对于常用钢：X_M=50K·N^-3/4·s¹/2·m^-1/2·mm；

X_J——啮入系数；

XГ——载荷分担系数；

w_Bt——端面单位载荷（N/mm）；

n₁——小轮转速（r/min）；

ρ_yrel——局部相对曲率半径（mm）；

ρ_y1——小轮齿廓局部曲率半径，mm；

对圆柱齿轮：

ρ_y2——大轮齿廓局部曲率半径，mm；

对圆柱齿轮：

对于锥齿轮，ρ_y1和ρ_y2见式（6-258）和式（6-259）。

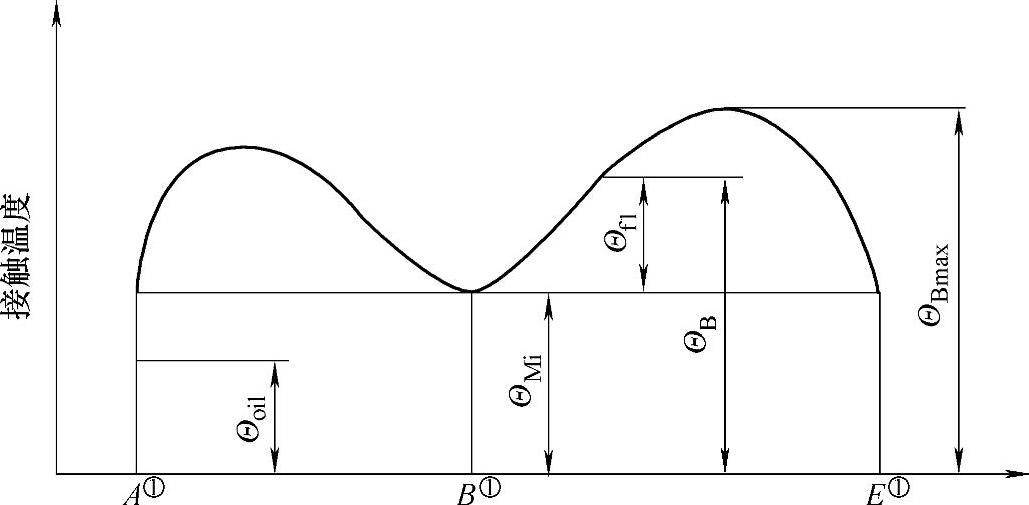
图6-83 沿接触轨迹的接触温度

①在啮合线上的位置。

对于Θ_fl更适用的表达形式，见第（9）节。

两个佩克莱特数必须足够高，以使它能满足几乎所有可能发生胶合的情况。当佩克莱特数较低时，热量从接触带区流向整个轮齿，引起不同的温度分布，此时式（6-224）和式（6-227）无效。

式中 ρ_M1——小轮材料的密度（kg/m³）；

ρ_M2——大轮材料的密度（kg/m³）；

c_M1——小轮单位质量的比热[J/（kg·K）]；

c_M2——大轮单位质量的比热[J/（kg·K）]；

λ_M1——小轮的热导率[N/（s·K）]；

λ_M2——大轮的热导率[N/（s·K）]。

对于圆柱齿轮和锥齿轮sinγ₁=sinγ₂=1。

3）端面单位载荷 圆柱齿轮端面单位载荷：

锥齿轮端面单位载荷：

式中 F_t——节圆上的名义切向力（N）；

b——齿宽（mm）；

b_eff=0.85b （6-234）

K_A——使用系数（对于圆柱齿轮，见GB/T 3480—1997，对于锥齿轮，见GB/T10062.1—2003）；

K_V——动载系数（对于圆柱齿轮，见GB/T 3480—1997，对于锥齿轮，见GB/T10062.1—2003）；

K_Bβ——胶合承载能力计算的齿向载荷分布系数；

K_Bβ=K_Hβ（6-235）

圆柱齿轮和锥齿轮的K_Hβ分别见GB/T 3480—1997和GB/T 10062.1—2003；

K_Bα——胶合承载能力计算的齿间载荷分配系数；

K_Bα=K_Hα（6-236）

圆柱齿轮和锥齿轮的K_Hα分别见GB/T 3480—1997和GB/T 10062.1—2003；

K_mp——分支系数。

分支系数K_mp是考虑多分支传动时，每个分支上载荷分配不均匀的系数。如果没有可靠的分析数据可用时，可用下列方法确定：

——对于具有n_p（n_p≥3）个行星齿轮的行星齿轮传动：

——对于在满载下，齿轮空心轴扭转角为Φ（°）的双联齿轮：

K_mp=1+（0.2/Φ） （6-238）

——对于外加轴向力为F_ex的双斜齿轮：

——对于其他情况：

K_mp=1 （6-240）

4）本体温度的分布 齿轮传动最主要的摩擦损失是轮齿啮合区的摩擦损失。其损失形式主要由于轮齿的摩擦而产生热量。由于多余的供油侧面排放消耗的机械“泵”能，有时不能忽略。由轴承（滚动轴承或滑动轴承）产生的损失是另一种不可避免的摩擦损失。对于高速齿轮传动，滑动轴承产生的热量可能比齿轮啮合产生的热量大得多。另一些热源是搅油和油封的摩擦。所有以上热源有下列共同特点：

——对于每种热源，流体的摩擦取决于各自运转条件下的润滑油粘度；

——所有热源的热量是相互联系的，通过传动元件到散热装置，如周围的空气或冷却系统。

热量的相互联系可用下列计算方法：

——离散组元的有限元法；

——扩散图法；

——热网络类比法。

接触面的本体温度Θ_Mi可以适当地取两个相接触轮齿的整体本体温度Θ_M1和Θ_M2的平均值。

下式为较精确的近似公式（在佩克莱特数较高时）：

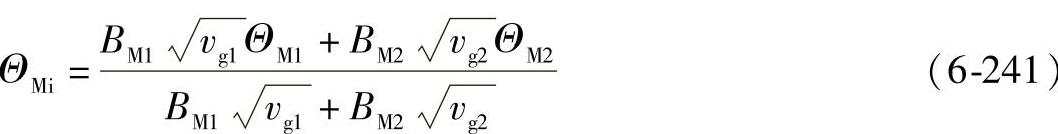
当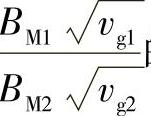的比值在一个相当广的范围内时，可用简单的数学平均式来近似计算：

当闪温长期超过150℃时，可能对齿面疲劳有不利的影响。

5）本体温度的粗略近似 为了粗略地研究本体温度，可用油温（要考虑喷油润滑对热传递带来的一些阻碍因素）加上决定闪温温度的那一部分取最大值之和来估算。

Θ_M=Θ_oil^+0.47XS X_mpΘ_flm （6-243）

式中 X_S——润滑方式系数，对于喷油润滑：X_S=1.2；对于油浴润滑：X_S=1；对于具有附加喷油润滑冷却的啮合：X_S=1.0；对于为提供足够的冷却而将齿轮浸没在油中时：X_S=0.2；

X_mp——多点啮合小轮系数，对于一个小轮与n_p个大轮啮合：

Θ_flm——沿接触轨迹的平均闪温（℃）：

然而，为了可靠地评价胶合的危险性，重要的是在分析中，要用齿轮本体温度的精确值来替代粗略的近似值。

（4）摩擦因数

在一个啮合周期内，影响齿轮轮齿间摩擦的一些因素是变化的。两个啮合齿面间存在相对运动，且在一个齿面是均匀的加速，而在另一个齿面上是均匀的减速。仅在节点位置是纯滚动。在任何其他位置都存在滚动和滑动。作用在两啮合齿面上的载荷也随着啮合位置的变化而变化。这些因素引起油膜厚度、润滑状态和摩擦因数的连续变化。即使在相同的啮合位置，对于不同的轮齿和不同时间，摩擦因数也可能是变化的。

为消除各种影响，认为局部摩擦因数适用于相关局部点处摩擦因数的示值。通过计算或测量来几何确定局部摩擦因数的变化是很困难的。因此，用代表性的摩擦因数的平均值来代替局部摩擦因数的值。

通常所使用的是摩擦因数的平均值（沿接触轨迹），即使这个值是变化的。在实验报告中，常常忽略了一些重要的影响因素，例如确定入口粘度的本体温度和润滑状况。

平均摩擦因数^[4]_μm取决于端面啮合线的几何参数、切向速度、法向载荷、入口粘度（相同于轮齿在本体温度处的粘度）、压粘系数、当量弹性模量、表面粗糙度、法向相对曲率半径。其他的一些影响因素（如公式中的和使用现场的）也必须要考虑，当然，要取决于进一步的研究。通过量纲的分析，有些很小的影响量可能被略去，影响量的数目可能会减少。

可用各种方法来测量和估算摩擦因数，应根据摩擦因数来选择极限接触温度。

1）平均摩擦因数，A法 用齿轮实验或柱—环实验方法测出开始胶合时的摩擦因数。此法的极限接触温度相对较高。

2）平均摩擦因数，B法 根据经验，在有规则的工作条件下使用较小的摩擦因数，最后计算摩擦因数可用一些合适的公式进行，即这些公式包含了相当于齿轮本体温度的动力粘度_ηL。此法的极限接触温度相对较低，见第（8）节。

3）平均摩擦因数，C法 如果计算开始时，还不知道本体温度，通常工作条件下的平均摩擦因数可用下式计算：

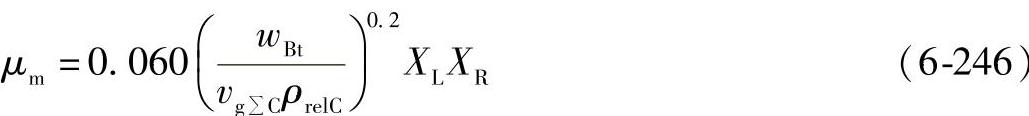
式中 w_Bt——切向单位载荷，见式（6-232）或式（6-233）（N/mm）；

v_g∑C——节点的切向速度之和（m/s）；

v_g∑C=2v_tsinα_wt （6-247）

v_t——节圆线速度（m/s），如果v_t>50m/s时，在式（6-247）中取v_t=50m/s；

ρ_relC——端面相对曲率半径（mm）（当啮合线上任意点的参数Г_y=0时，按式（6-227）计算）；

X_L——润滑剂系数：

η_oil——在油温Θ_oil下的动力粘度（mPa·s）；

X_R——粗糙度系数

Ra₁——跑合前的小轮齿面粗糙度Ra（μm）（适当跑合后Ra₁可降低到初始值的大约60%）；

Ra₂——跑合前的大轮齿面粗糙度Ra（μm）（适当跑合后Ra₂可降低到初始值的大约60%）。

（5）啮合线上的参数

啮合线上的点用无量纲线性参数Г_y来表示，在啮合线与小轮基圆的切点处Г_y为-1，在节点处Г_y为0，见图6-84。

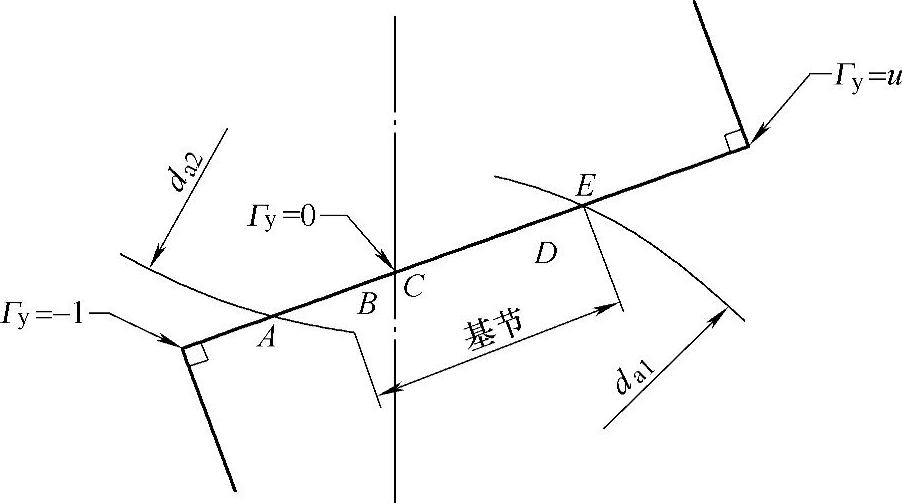
图6-84 啮合线上的参数

在接触轨迹上的任意点处：

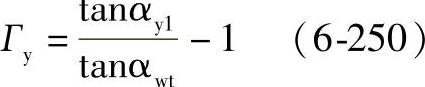
在接触轨迹的下界点处：

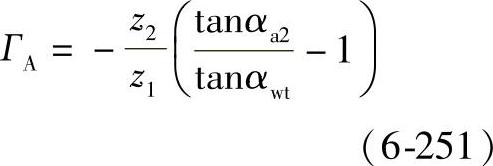
在单对齿啮合区下界点处：

在单对齿啮合区上界点处：

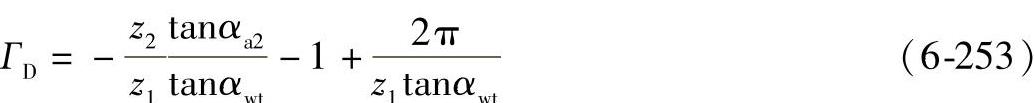
在接触轨迹的上界点处：

上述式中，齿顶压力角定义为

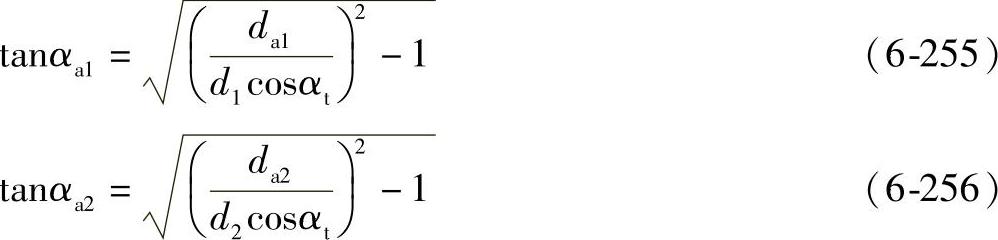
锥齿轮的参数既可以用当量几何参数来计算[见本章8.3.1节（7）]，也可以用下述公式计算（也适用于轴交角Σ=δ₁+δ₂不等于90°时的情况）。

在啮合线上的任意点处：

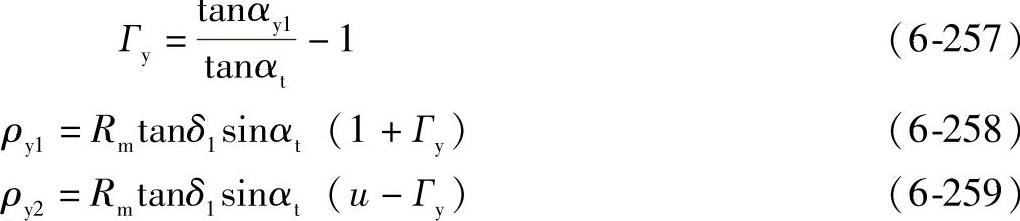
在啮合线上的特征点处：

上述式中，压力角被定义为

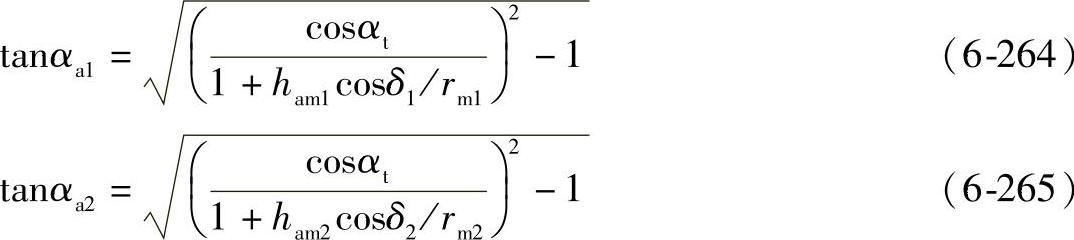
式中 δ₁——小轮的节锥角（°）；

δ₂——大轮的节锥角（°）；

R_m——中点（齿宽中点）锥距（mm）；

h_am1——小轮齿宽中点齿顶高（mm）；

h_am2——大轮齿宽中点齿顶高（mm）；

r_m1——小轮齿宽中点节圆半径（mm）；

Г_m2——大轮齿宽中点节圆半径（mm）。

（6）啮入系数

啮入系数是根据经验考虑，由于啮合开始时齿面上还未形成油膜而使胶合的危险性增加的系数。对于较大的齿轮其影响相对较大。

啮入系数为：

——对于小轮驱动大轮（减速）

当Г_y≥0时

X_J=1 （6-266）

当Г_y＜0时

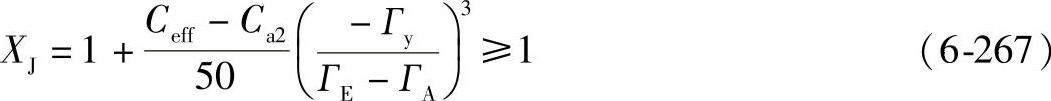
——对于大轮驱动小轮（增速）

当Г_y≤0时

X_J=1 （6-268）

当Г_y＞0时

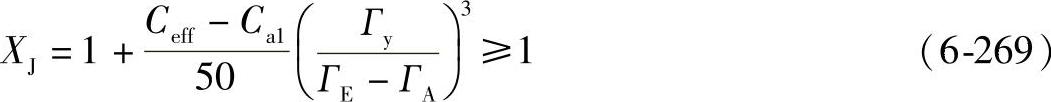
式中 C_eff——最佳齿顶修缘量（μm）；

C_a1——小轮的齿顶修缘量（μm）；

C_a2——大轮的齿顶修缘量（μm）；

Г_y——啮合线上任意点的参数；

Г_A——啮合线上A点的参数；

Г_B——啮合线上B点的参数。

（7）载荷分担系数

载荷分担系数XГ是考虑后续啮合的轮齿上的载荷分担的系数。根据常规，载荷分担系数表示为啮合线上线性参数Г_y的函数。当前面的轮齿结束啮合时，在端面双齿啮合区的啮入轨迹上，载荷分担系数增加，当后面的轮齿进入啮合时，在端面双齿啮合区的啮出轨迹上，载荷分担系数减少。

由于前面啮合的轮齿的误差，可能引起理论载荷分担系数的瞬时增加或减少，这与由稍晚一点进入啮合的后续轮齿的误差引起的载荷分担系数的瞬时增加或减少无关。

对于圆柱齿轮，XГ的值不超过1.00，它指的是所有端面单对齿啮合区。由于动载荷不规则变化的位置可能引起端面单对齿啮合区的扩大。

载荷分担系数XГ取决于齿轮传动类型和齿廓修形。在有斜齿（偏向齿体内的齿廓修形）支撑的情况下，载荷分担系数与支撑系数X_but一起考虑。

齿廓修形（齿顶修缘）公式见第（10）节。

1）支撑系数 对于斜齿轮，由于接触线的倾斜，在啮合线上的两端A点和E点附近可能有一个支撑的影响。这个影响适用于齿顶修缘量小于最佳值（C_a＜C_eff）时的圆柱齿轮和锥齿轮。

支撑系数用X_but表示，可简化为A—AU、AU—EU、EU—E范围内的线性函数，见图6-85。

X_but可用下述式子表达：

对圆柱齿轮

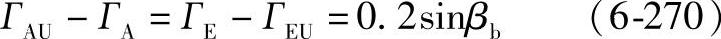
对锥齿轮

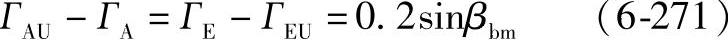
当ε_β≥1时

X_butA=XbutE=1.3 （6-272）

当ε_β＜1时

对于Г_A≤Г_y<Г_AU时

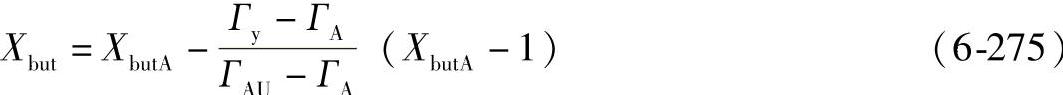
对于Г_AU≤Г_y≤Г_EU时

X_but=1（6-276a）

对于Г_EU＜Г_y≤Г_E时

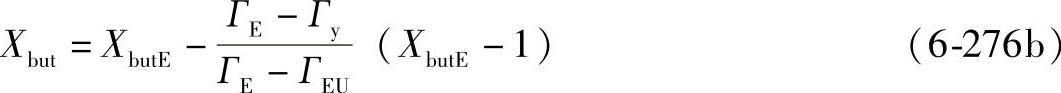
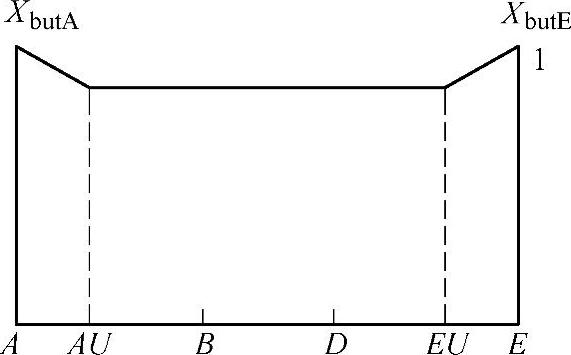
图6-85 支撑函数

2）齿廓未修形的直齿轮 通常认为齿廓未修形的直齿轮的载荷分担系数值是个不连续的矩形，见图6-86。然而，由于存在制造误差，在每个双啮区内，对于凸出的齿廓，载荷分担系数将增加，对于其他齿轮，载荷分担系数将减少。不同精度等级齿轮的载荷分担系数是一个包络线族，见图6-87。

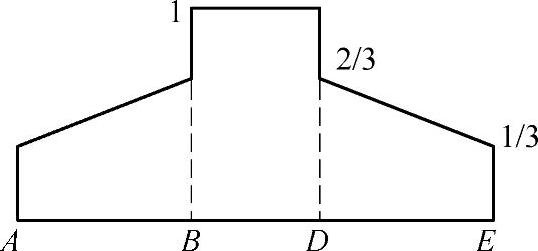
图6-86 齿廓未修形的直齿圆柱齿轮的载荷分担系数（精度等级Q为7级或7级以上）

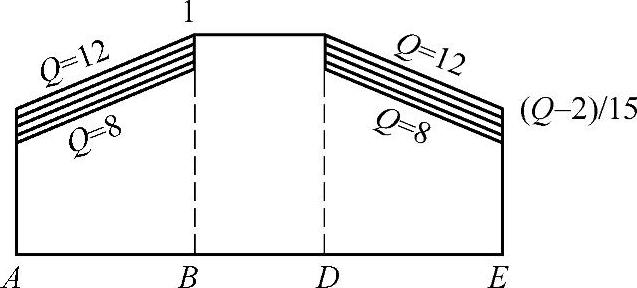
图6-87 齿廓未修形的直齿圆柱齿轮的载荷分担系数（精度等级Q为8级或8级以下）

对于Г_A≤Г_y＜ГB

对于Г_B＜Г_y≤Г_DXГ=1

对于Г_D≤Г_y≤ГE

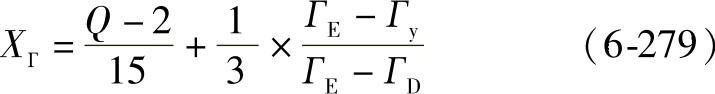
当精度等级Q为7级或7级以上时

Q=7（6-280）

当精度等级Q为8级或8级以下时，取Q=精度等级。

3）齿廓修形的直齿轮 见图6-88和图6-89。

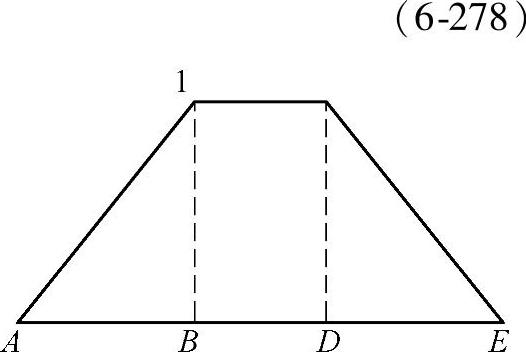
图6-88 具有最佳齿廓修形的直 齿圆柱齿轮的载荷分担系数

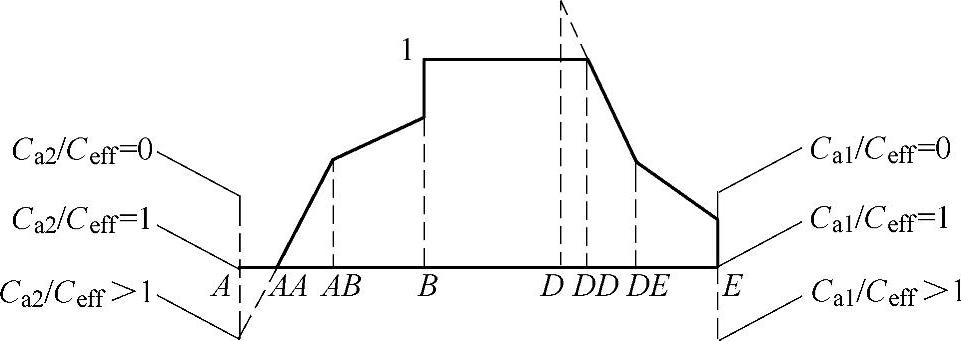
图6-89 在A点附近具有偏向体外的齿廓修形，而在E点附近具有偏向体内的 齿廓修形的直齿圆柱齿轮的载荷分担系数

对于Г_A≤Г_y≤ГAB

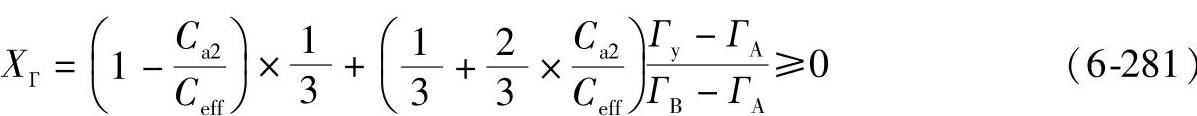
对于Г_AB≤Г_y≤ГB

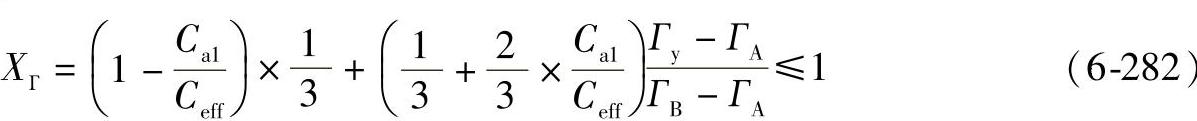
对于Г_B≤Г_y≤Г_D

XГ=1（6-283）

对于Г_D≤Г_y≤ГDE

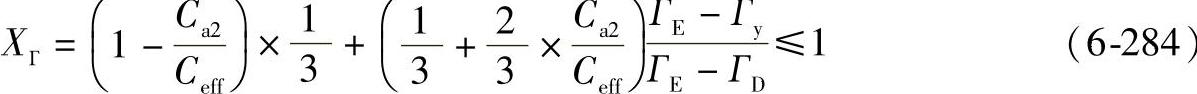
对于Г_DE≤Г_y≤ГD

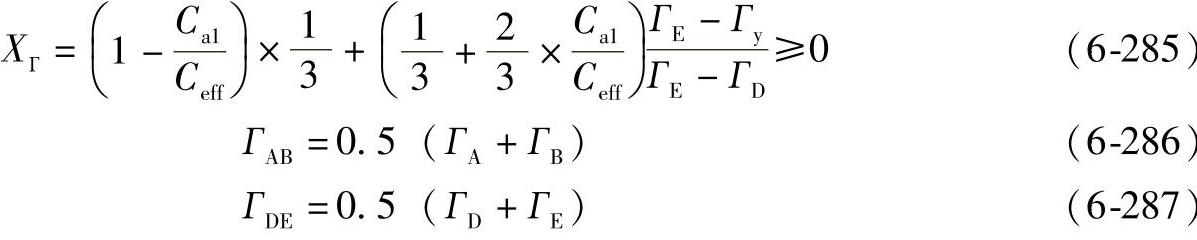
对于C_a2＞Ceff

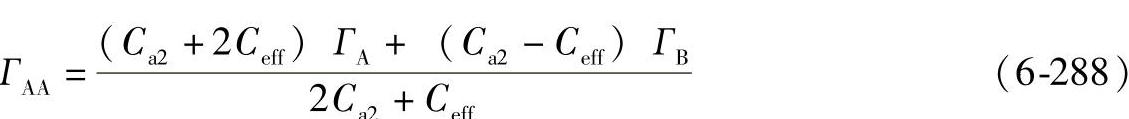
对于C_a2≤C_eff

Г_AA=Г_A （6-289）

对于C_a1＞Ceff(www.daowen.com)

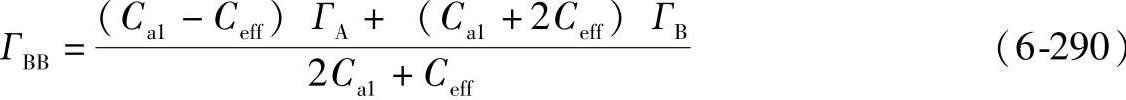
对于C_a1≤C_eff

Г_BB=Г_B （6-291）

对于C_a2＞Ceff

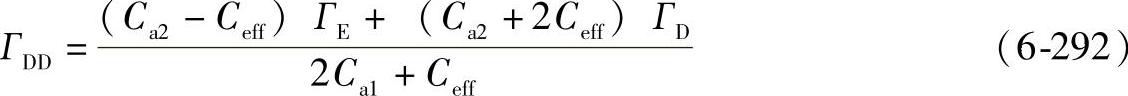
对于C_a2≤C_eff

Г_DD=Г_D （6-293）

对于C_a1＞Ceff

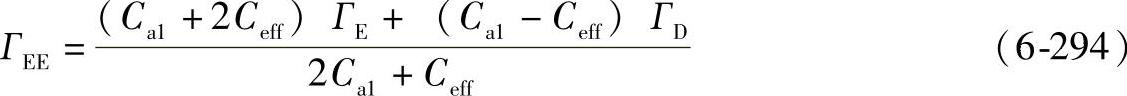
对于C_a1≤C_eff

Г_EE=Г_E （6-295）

4）齿廓未修形的窄斜齿轮 对于总重合度较小（ε_γ＜2）的斜齿轮仍然有单齿啮合区。因此，考虑到端面的几何参数以及支撑的影响，这种斜齿轮可以与直齿轮类似处理。见图6-90。

未修形的窄斜齿轮的载荷分担系数由（7）2）中的X_Г乘以支撑系数X_but获得。

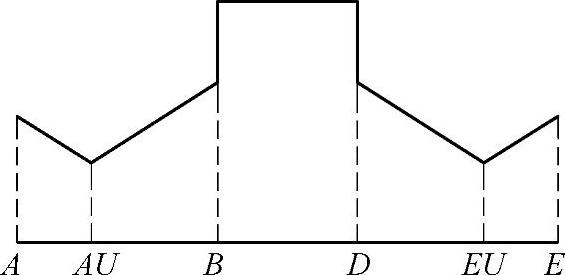
图6-90 齿廓未修形并考虑支撑影响的窄斜齿轮的载荷分担系数

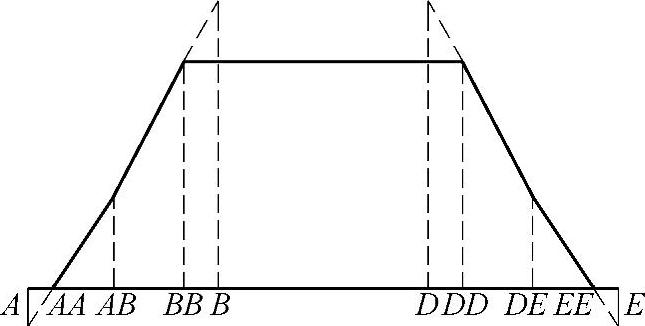
图6-91 具有最佳或偏向体外的齿廓修形的窄斜圆柱齿轮的载荷分担系数

5）齿廓修形的窄斜齿轮 总重合度较小（ε_γ＜2）的斜齿轮仍然有单齿啮合区。因此，考虑到端面的几何参数，这种斜齿轮可以与直齿轮类似处理。见图6-91和图6-92。

这种齿轮的载荷分担系数由（7）2）中的X_Г乘支撑系数X_but获得。

6）齿廓未修形的宽斜齿轮 对于宽斜齿轮（ε_γ＜2），在倾斜接触线的末端，局部啮合刚度较高，此时，假定支撑的影响作用在沿斜齿的A点和E点附近的一个恒定长度上，这个长度相对于端面的长度为0.2sinβ_b，见图6-93、图6-85和（7）1）。

此时，载荷分担系数由表示平均载荷的值1/ε_α乘以支撑系数X_but获得：

图6-92 具有偏向体内的齿廓修形的窄斜齿轮的载荷分担系数

图6-93 齿廓未修形的圆柱宽斜齿轮的载荷分担系数

7）齿廓修形的宽斜齿轮 假定在接触轨迹两端的A—AB段和DE—E段的齿顶修缘长度相等，并导致未加载齿轮的端面重合度为ε_α=1，见图6-94。具有偏向体内或偏向体外齿廓修形的圆柱宽斜齿轮（ε_γ≥2）的载荷分担系数，在具有支撑影响的未修形齿廓和最佳齿廓修形的载荷分担系数之间分别用内插法或外插法确定，见图6-95。

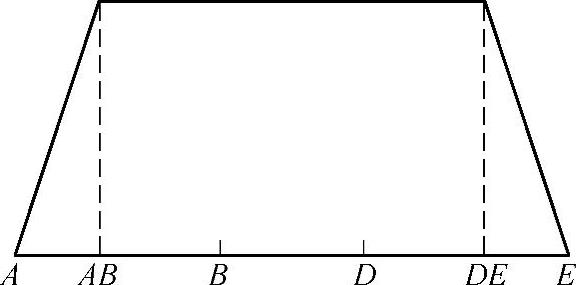
图6-94 具有最佳齿廓修形的圆柱宽斜齿轮的载荷分担系数

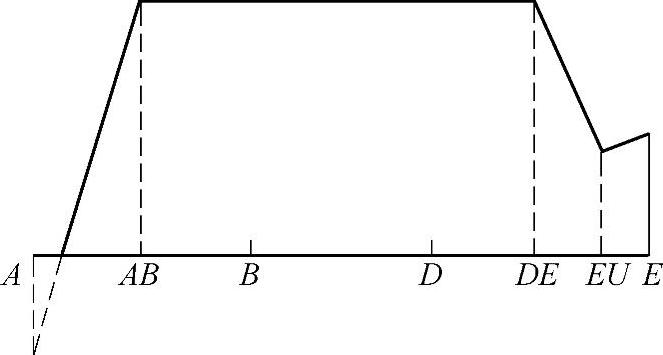
图6-95 在A点附近具有偏向体外、在E点附近具有偏向体内的齿廓修形的圆柱宽斜齿轮的载荷分担系数

用以下的各点来区分这些不同的范围：

对于C_a2≥Ceff

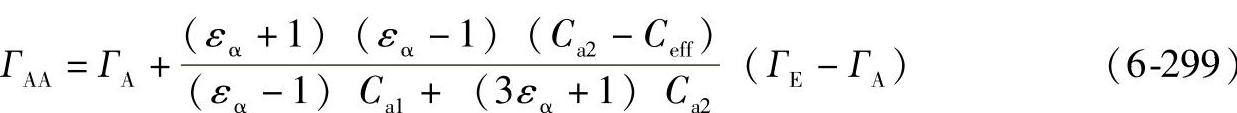
对于C_a1≥Ceff

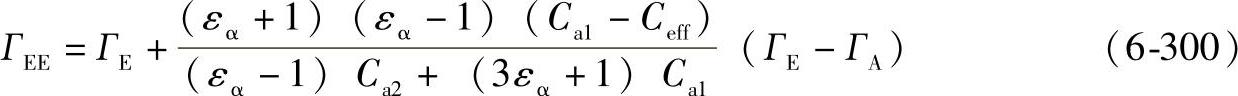
对于C_a2＜C_eff，Г_AA≤Г_y≤Г_AB或对于C_a2≥C_eff，Г_A≤Г_y≤ГAB

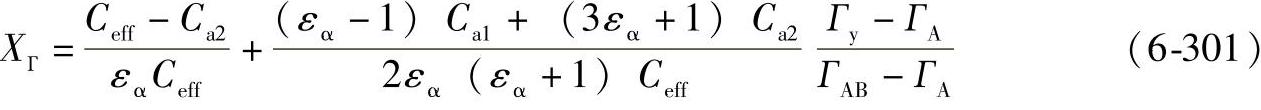
对于C_a2≥C_eff，Г_AA≤Г_y≤Г_AB

XГ=0 （6-302）

对于C_a2≥C_eff，Г_AB≤Г_y≤ГDE

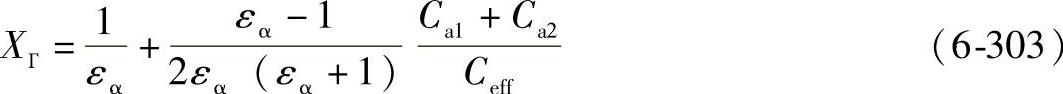
对于C_a1<C_eff，Г_DE≤Г_y≤Г_E或对于C_a1≥C_eff，Г_DE≤Г_y≤ГEE

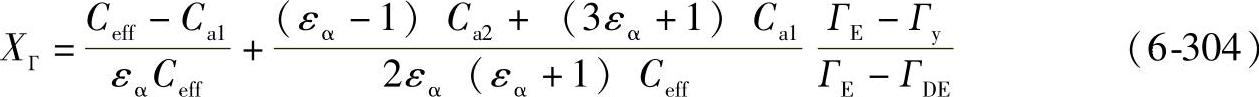
对于C_a1≥C_eff，Г_DE≤Г_y≤Г_EE

X_Г=0 （6-305）

8）窄锥齿轮 具有齿廓修形（C_a＜C_eff）的窄锥齿轮（ε_γ＜2），载荷分担系数XГ在按（7）4）计算的XГ（C_a=0）和按（7）9）计算的XГ（C_a=C_eff）之间用线性内插法确定。记住X_but。

具有齿廓修形（C_a≥C_eff）的窄锥齿轮（ε_γ＜2），载荷分担系数XГ按（7）9）计算。

9）宽锥齿轮 具有最佳齿廓修形（C_a1=C_eff，C_a2=C_eff）的宽锥齿轮，假定载荷分担系数为抛物线形，见图6-96。

中点M的定义为

最佳齿廓修形（C_a1=C_eff，C_a2=C_eff）的载荷分担系数：

如果齿廓修形量C_a1与C_a2不同，那么在M点曲线不连续，AM段和ME段应分别计算，见图6-97。

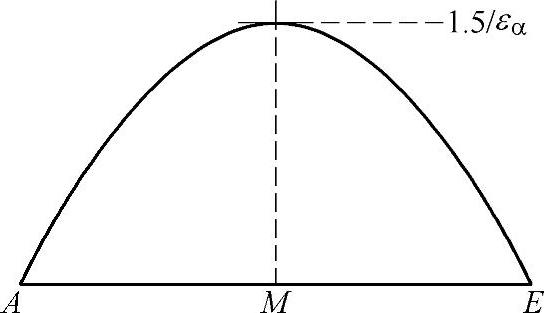
图6-96 具有最佳齿廓修形锥齿轮的载荷分担系数

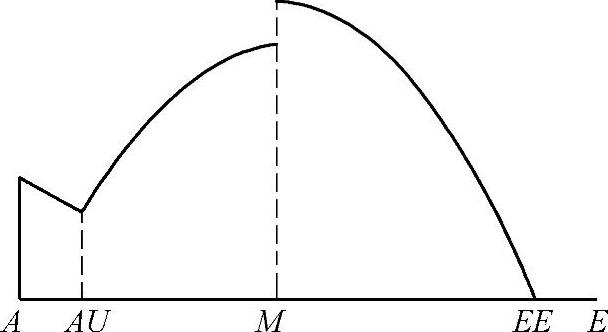
图6-97 在A点附近具有偏向体内的齿廓修形、在E点附近具有偏向体外的齿廓修形锥齿轮的载荷分担系数

对于偏向体内的齿廓修形，载荷分担系数在具有支撑影响[见（7）6）]的未修形齿廓的载荷分担系数和最佳修形齿廓的抛物线形载荷分担系数之间用内插法确定。

对于偏向体外的齿廓修形，抛物线有一个新的端点AA或EE。

对于偏向体内的齿廓修形，X_Г在具有最佳齿廓修形的X_Г[式（6-307）]和齿廓未修形时的X_Г[式（6-296）]之间用线性内插法确定。插值确定应分段进行，即受C_a2影响的AM段和受C_a1影响的ME段。

对于偏向体外的齿廓修形，则有新的端点AA和EE。

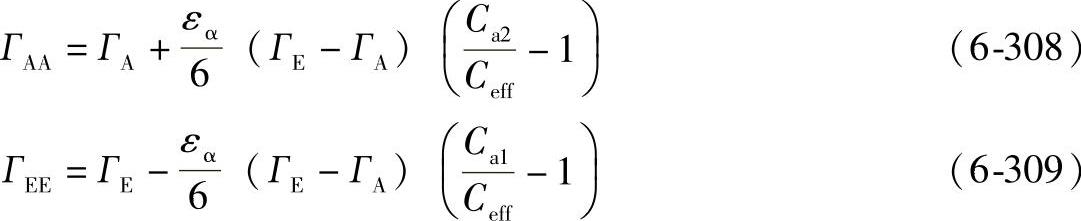
对于Г_A≤Г_y≤Г_AA

X_Г=0 （6-310）

对于Г_AA＜Г_A≤ГM

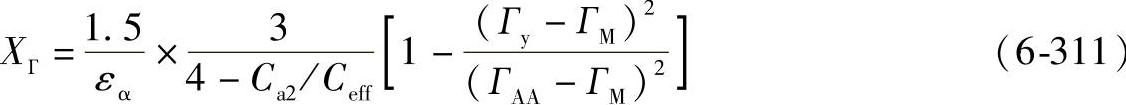
对于Г_M＜Г_A≤ГEE

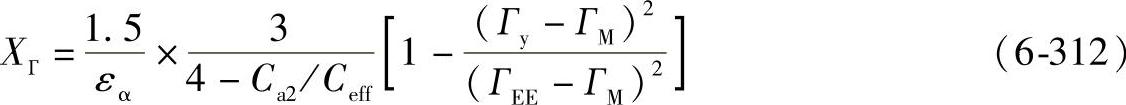
对于Г_EE≤Г_y≤Г_E

X_Г=0 （6-313）

（8）胶合温度和安全性

1）胶合温度 胶合温度是根据所选择的润滑油和齿轮材料的组合可能发生胶合时的接触温度。认为一对齿轮的材料-润滑油-材料系统的胶合温度有一个特定的值，这个值由相同材料-润滑油-材料系统的齿轮试验来确定。

当使用较低添加剂的矿物油时，认为在相当广的范围内胶合温度与工作条件无关。

当使用具有抗胶合或减磨添加剂的矿物油或合成油时，对于不同的材料和工作条件下，胶合温度可能是非恒定值这一特性的确定仍需进一步研究。尤其应注意的是试验条件和实际工作条件或设计条件之间的修正，转换图中（见图6-82）所显示的特性可能对这种修正的影响很大。

2）组织系数 引入经验性的组织系数后，具有较低添加剂矿物润滑油，由齿轮试验确定的胶合温度，可扩展到不同的齿轮钢、热处理或表面处理。

_s=Θ_MT+X_WΘ_flmaxT （6-314）

式中 Θ_MT——试验齿轮的闪温（℃）；

Θ_flmaxT——试验齿轮的最大闪温（K）；

X_W——组织系数（见表6-37）。

然而，对于通常的工作条件和使用热弹系数的平均值时，组织系数的这个近似值受所用摩擦因数的方法的限制。如果所使用的方法是考虑摩擦因数和热弹系数的真实值时，则不必再使用组织系数。

3）瞬时接触时间 试验表明：用抗胶合油润滑时，齿轮的胶合温度受瞬时接触时间的影响。瞬时接触时间是指齿面上的一点暴露在相啮齿的赫兹接触带内的时间。

表6-37 组织系数

一对齿面确定的瞬时接触时间t_max为t₁和t₂中的最大值。

胶合温度Θ_s和接触温度之间关系可近似地用图6-98所示的由两条直线组成的曲线表达。

对于t_max＜t_c

Θ_s=Θ_sc+X_ΘX_W（t_c^-tmax） （6-317）

对于t_max≥t_c

Θ_s=Θ_sc （6-318）

式中 Θ_sc——较长接触时间的胶合温度（℃）；

X_Θ——胶合温度梯度（K/μs）；

X_W——组织系数；

t_c——曲线弯曲处的瞬时接触时间（μs）；

t_max——啮合齿的瞬时接触时间（μs）。

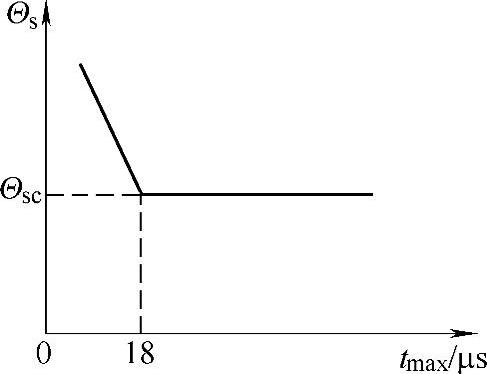
图6-98 对于加抗胶合添加剂润滑油瞬时接触时间对胶合温度的影响

对于不同润滑油X_Θ和t_c可用下列值：

——不加抗胶合添加剂：X_Θ=0K/μs，t_c=0μs；

——加抗胶合添加剂：X_Θ=18K/μs，t_c=18μs。

4）齿轮试验的胶合温度 胶合温度可由齿轮试验确定，如Ryder、FZG-Ryder、FZGL-42、FZGA/8.3/90等方法。

试验结果的表达应包括胶合温度和试验条件。如果试验结果用其他方式表达，则应给出关系式，如：

Θ_s=80+（0.85+1.4X_W）X_L（S_FZG）2 （6-319）

式中 X_W——组织系数（见表6-37）；

X_L——润滑油系数[见式（6-248）]；

S_FZG——FZG A/8.3/90试验的载荷级，这里指的是发生胶合时载荷级。

然而，油的参数变化容易引起S_FZG更大的变化，假定在换油间隔期间油稍微有点变质，载荷级的变化通常为±1。因此，计算时可用比规定载荷级较小的载荷级。

5）安全范围 与疲劳损伤的时间较长相比，一次简单的瞬时过载就会引起严重的胶合使齿轮在较短的时间失效。因此在选择合适的安全范围时，应谨慎考虑，尤其要注意运行时节线速度较高的齿轮。

在较短瞬时接触时间t_max情况下，安全条件是基于胶合温度的增加（Θ_s>Θ_sc）[见（8）3）]，而瞬时接触温度t_max不应该增加，除非传动功率适当降低。

安全系数定义为

式中 Θ_s——胶合温度（℃）；

Θ_Bmax——最大接触温度（℃）；

Θ_oil——油温（℃）。

然而，齿轮的实际载荷与确定的接触温度之间的关系很复杂，用温度的任何比值来表达安全系数可能会引起混淆。

因此，除了试验载荷级的说明以外[见（8）4）节]，建议用胶合温度与计算的最大接触温度之间所要求的最小差别（如≥50K）来表达安全概念。

（9）闪温公式提示

自从最初的闪温公式公布以来，布洛克又作了下列修改：

——将赫兹接触带的全宽改为半宽，并用椭圆形摩擦热分布的1.11代替抛物线形摩擦热分布的0.832=1.17；

——扩展到不同方向的切线速度，见式（6-224）。

为方便起见，作了确切的修改；

——有些量用另一些量来表达，如赫兹接触带半宽和曲率半径；

——公式的某些部分被集中为独立的系数，如热弹系数。

为实际应用，作了适当的修改：

——重新定义的系数，如载荷分担系数；

——增加了经验系数，如啮入系数。

1）常用情况 在轮齿接触的最通常的情况（如准双曲面齿轮）中，认为连续接触区呈锥形带状，见图6-99。两轮的切向速度v_g1和v_g2的方向角γ₁和γ₂不同，γ₁和γ₂分别为v_g1和v_g2与接触区长轴的夹角。在较简单的情况下（如圆柱齿轮），方向角简化为γ₁=γ₂=π/2。

锥形接触区的一些横截面上的接触压力分布近似于半椭圆分布，半椭圆在处于两平行平面之间的替代带状接触区上，带状接触区有一个均匀的宽度且等于前述的局部宽度，见图6-99。

准双曲面齿轮的实际赫兹接触区可假定为椭圆形，并且切向速度方向与接触区长轴的方向既不垂直也不平行。然而，椭圆接触区可能相当长，有足够高的椭圆率，或它可能是稍有锥度的带状。

两个切线速度的方向偏离椭圆短轴不太多。换句话说，让两个速度在长轴上有一个分量。

为了寻找确定最大闪温，实际椭圆接触区由一个带状接触区来代替，带状接触区的宽度为2b_H等于椭圆短轴的长度，见图6-99。

图6-99 两轮切线速度方向不同的替代带状接触区

注意：最大接触压力（在短轴上）直接与载荷的立方根而不是平方根成正比。在一些情况下，为了延长点接触，必须采用赫兹公式。

总之，目前的方法可以说是一个合理的近似方法。主要原因在于这样的特征：即在上述定义的动态条件下，对于实际的足够长的椭圆接触，希望实际最大闪温发生在接近短轴的一个点上。

对于替代带状接触且切向速度方向不同时，布洛克闪温公式为

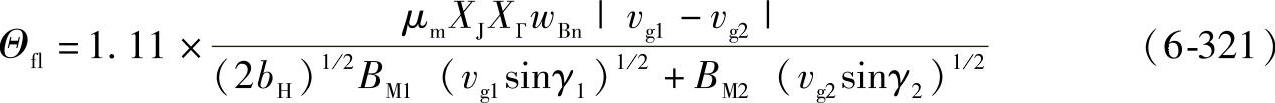
式中 μ_m——平均摩擦因数；

X_J——啮入系数；

XГ——载荷分担系数；

w_Bn——法向单位载荷（N/mm）；

w_Bt——端面单位载荷（N/mm），见（3）3）；

α_wn——法向啮合角（°）；

α_wn=arcsin（sinα_wtcosβ_b）（6-323）

β_w——啮合螺旋角（°）；

b_H——赫兹接触带半宽（mm）；

v_g1——小轮的切向速度（矢量）（m/s）；

v_g2——大轮的切向速度（矢量）（m/s）；

B_M1——小轮的热接触系数[N/（mm¹/2·m¹/2·s¹/2·K）]，见（9）3）；

B_M2——大轮的热接触系数[N/（mm¹/2·m¹/2·s¹/2·K）]，见（9）3）；

γ₁——小轮切向速度的方向角（°）；

γ₂——大轮切向速度的方向角（°）。

2）圆柱齿轮　圆柱齿轮所使用的闪温公式^[5]为

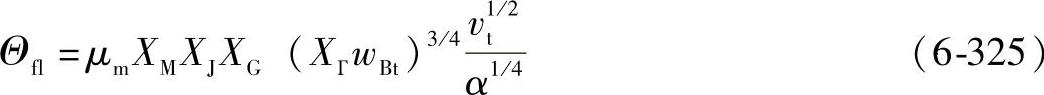
式中 μ_m——平均摩擦因数；

X_M——热弹系数；

X_J——啮入系数；

X_G——几何系数；

对于外齿轮副：

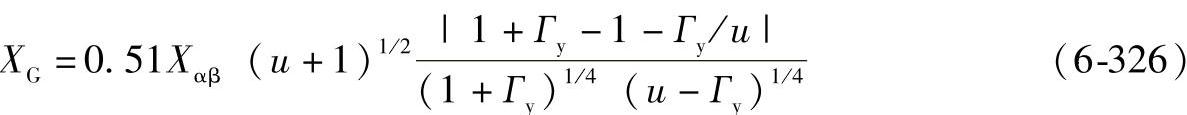
对于内齿轮副（实际上是符号的转换）

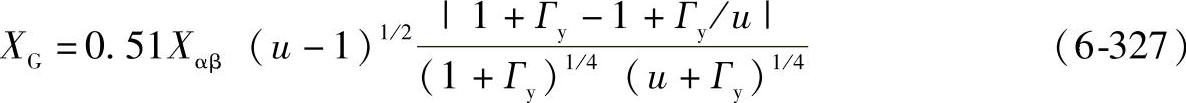
X_Г——载荷分担系数；

w_Bt——端面单位载荷；

v_t——节线速度；

α——中心距。

法向压力角和螺旋角的影响为

X_αβ=1.22sin¹/4α_wtcos^-1/2α_wtcos¹/2β_b （6-328）

然而，系数X_αβ的值非常接近于^[6]1，见表6-38，它的近似值可取为1。

3）热弹系数 热弹系数是考虑大、小齿轮材料特性的影响。

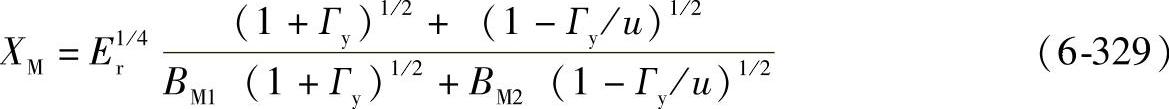
式中 E_r——当量弹性模量（N/mm²）；

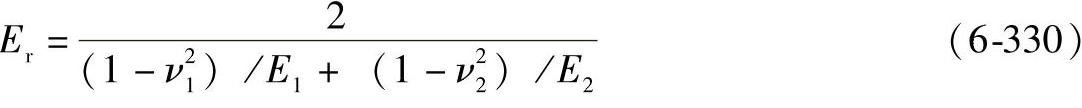
E₁——小轮材料的弹性模量（N/mm²）；

E₂——大轮材料的弹性模量（N/mm²）；

ν₁——小轮材料的泊松比；

ν₂——大轮材料的泊松比；

表6-38 系数Xαβ

B_M1——小轮的热接触系数[N/（mm^1/2·m^1/2·s^1/2·K）]；

B_M2——大轮的热接触系数[N/（mm^1/2·m^1/2·s^1/2·K）]。

B_M1=（0.001λ_M1ρ_M1c_M1）^1/2 （6-331）

B_M2=（0.001λ_M2ρ_M2c_M2）^1/2 （6-332）

式中 λ_M1——小轮材料的热传导系数[N/（s·K）]；

λ_M2——大轮材料的热传导系数[N/（s·K）]；

ρ_M1——小轮材料的密度（kg/m³）；

ρ_M2——大轮材料的密度（kg/m³）；

c_M1——小轮材料单位质量的比热[J/（kg·K）]；

c_M2——大轮材料单位质量的比热[J/（kg·K）]。

大多数情况下，大、小轮的热接触系数相同，热弹系数完全取决于材料特性。

对于马氏体钢：λ_M=41～52N/（s·K），ρ_Mc_M约为3.8N/（mm²·K）；因此，对这种钢，当热弹系数为未知时，可采用其平均值B_M=435N/（mm¹/2·m¹/2·s¹/2·K）=13.8N/（mm·s¹/2·K）而不会有太大的误差。对于用特种钢制造的齿轮：E₁=E₂=206000N/mm²，ν₁=ν₂=0.3，还有：

X_M=500K·N^-3/4·s¹/2·m^-1/2·mm （6-334）

4）锥齿轮 锥齿轮的连续接触区为稍带锥度的带状形。然而，在大多数情况，可较好地用平行的带状接触区来近似，连同两个切向速度的重合并在方向上与长轴垂直，尤其是当曲率半径的正确值和赫兹接触带已知时，可直接使用原来的式（6-321）。为方便起见，公式可以被改写，即用直线来近似“8”字作用线，并且系数用锥齿轮的一般量来表达。

对于改写的运动学公式作如下假设^[7]，见图6-100。

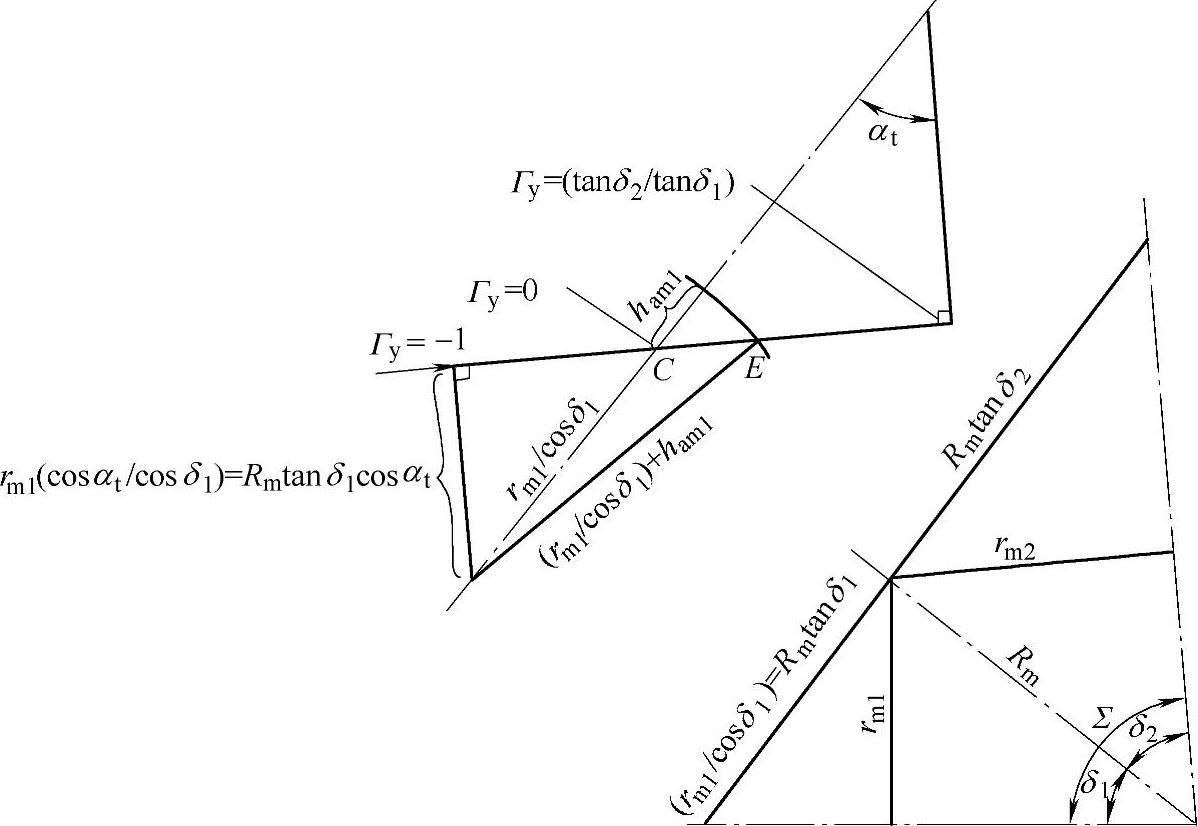
图6-100 近似作用线

——大、小轮有一个公共顶点并有任意轴交角：

Σ=δ₁+δ₂ （6-335）

——所有的计算与分锥有关；

——啮合线用直线近似；

——啮合面为一个平面。

锥齿轮的闪温既可以作为当量圆柱齿轮副来计算，也可以用直接的公式计算。

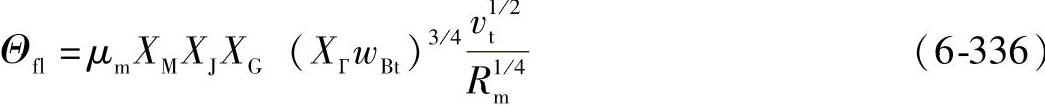
式中 μ_m——平均摩擦因数；

X_M——热弹系数；

X_J——啮入系数；

X_G——几何系数。

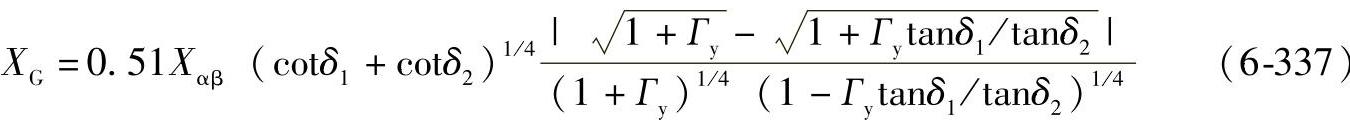
式中 X_αβ——角度系数；

X_Г——载荷分担系数；

w_Bt——端面单位载荷；

v_t——节线速度；

R_M——中点锥距。

（10）最佳齿廓修形

如果齿廓进行修形，修形量的设计和加工应满足要求的载荷分配，如图6-87。小轮和大轮的最佳齿顶修缘量可近似表达为

式中 K_A——使用系数；

K_mp——分支系数，见（3）3）；

F_t——切向力（N）；

b——齿宽（mm）；

α_t——端面压力角（°）；

c_γ——啮合刚度[N/（mm·μm）]。

圆柱齿轮的齿顶修缘高度在齿轮未加载时既不到达单对齿啮合区，也不能导致重合度ε_α<1（即计算ε_α时假定的顶圆直径等于修缘区开始的直径）。

如果相啮齿轮的齿根也修形，那么齿顶修缘量应该用当量齿顶修形量来代替，当量修形量为齿顶修缘量和相啮齿轮的偏向齿体内的齿根修形量之和。

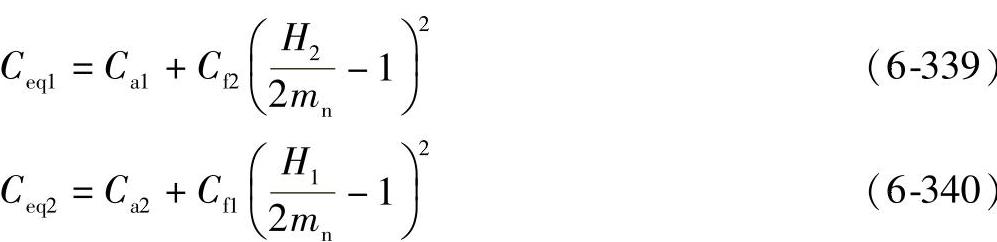
对于圆柱齿轮

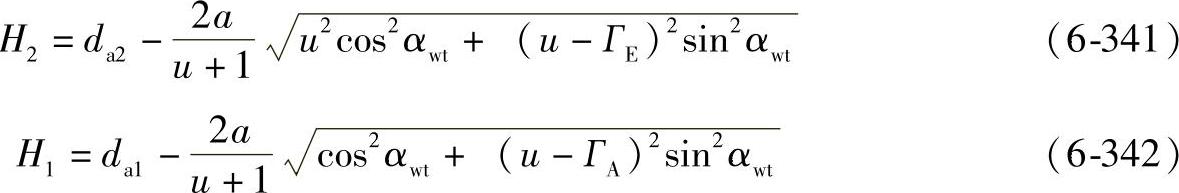
对于锥齿轮，使用当量齿轮的量值，见本章8.3.1节（7），或用下式：

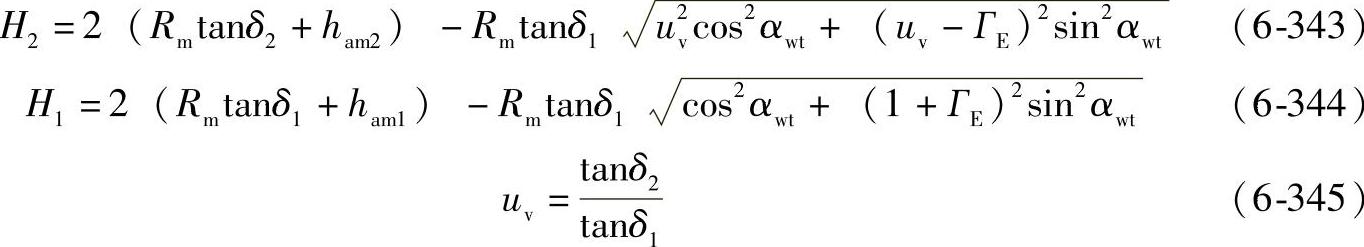
式中 m_n——法向模数（mm）；

d_a1——小轮顶圆直径（mm）；

d_a2——大轮顶圆直径（mm）；

α——中心距（mm）；

u——齿数比；

R_m——中点锥距（mm）；

δ₁——小轮的节锥角（°）；

δ₂——大轮的节锥角（°）；

h_am1——小轮齿宽中点齿顶高（mm）；

h_am2——大轮齿宽中点齿顶高（mm）；

α_wt——端面啮合角（°）；

Г_A——啮合线上A点的参数；

Г_E——啮合线上E点的参数。