本节所给出的基本公式用于计算最小轮缘厚度≥3.5m_mn的直齿和斜齿锥齿轮、零度齿锥齿轮和弧齿锥齿轮的齿根弯曲应力。把所有载荷对齿根应力的影响认为是齿轮传递的载荷所产生的应力，并作出定量的评价（例如，齿轮轮缘过盈配合引起的应力和轮齿加载引起的齿根应力相叠加得到的应力，在计算齿根应力σ_F或许用齿根应力σ_FP时应予考虑）。

本节内容不能用于应力大于10³次循环的极限应力的场合，否则应力会超过轮齿的弹性极限。

（1）轮齿折断和安全系数

通常轮齿折断使齿轮工作寿命结束，有时由于一个轮齿的折断引起齿轮箱的所有齿轮损坏；在某些情况时，会使输入和输出轴间的传动装置损坏。

因此，选用的弯曲强度安全系数S_F应大于接触强度安全系数S_H的平方（选用安全系数的一般说明见本章8.3.1节）。

弯曲强度的最小安全系数，对于弧齿锥齿轮应取S_Fmin≥1.3；对于直齿锥齿轮或β_m<5°的弧齿锥齿轮，应取S_Fmin≥1.5。最小安全系数的值建议由制造商和用户协商确定。

（2）计算轮齿弯曲强度的公式

比较下面的应力值，可以确定轮齿的抗弯承载能力：

——弯曲应力，根据轮齿的几何尺寸，制造精度，轮缘、轴承和轴承座的刚性，传递的转矩等，用齿根应力公式进行计算。

——许用应力，考虑齿轮运转时工作条件的影响，用许用齿根应力公式进行计算。

计算的齿根应力σ_F应小于许用齿根应力σ_FP。

1）齿根应力 大小齿轮的齿根应力按下式计算：

σ_F=σ_F0^KA KV KFβ KFα≤σFP （6-129）

式中 σ_F0——齿根应力基本值，其定义是一个理想的齿轮在名义转矩下引起的齿根处的最大拉应力。

K_A、K_V、KFβ、KFα见本章8.3.1节。

①齿根应力基本值σ_F0-B1——B1法。齿根应力基本值是根据齿根处（齿根圆角与30°切线相切处）最大的拉应力计算的。载荷作用的位置为：

a）单对齿啮合区外界点（ε_Vβ=0）。

b）接触区中点（ε_Vβ≥1）。

c）作用在a）和b）之间的位置。

用Y_ε把作用在齿顶的载荷转换到作用的位置。

式中 F_mt——齿宽中点分度圆锥上的名义切向力；

b——齿宽；

Y_Fa——齿形系数，Y_Fa是考虑载荷作用在齿顶时，齿形对名义弯曲应力的影响；

Y_sa——应力修正系数，Y_sa是考虑把载荷作用在齿顶时的名义弯曲应力转换为齿根应力基本值的系数，所以Y_sa考虑到齿根危险截面处（齿根圆角处）齿根应力增加的影响，和该处应力集中的影响一致，但不影响弯矩的力臂；

Y_ε——重合度系数，是考虑把载荷作用在齿顶时的齿根应力基本值，换算为载荷在作用位置时的齿根应力基本值；

Y_K——锥齿轮系数，是考虑较小的l_b′值与齿宽b的比及接触线倾斜的影响；

Y_LS——载荷分担系数，是考虑两对或多对相啮合轮齿间的载荷分配。

②齿根应力基本值σ_F0-B2——B2法。应用B2法时，用复合几何系数Y_P代替计算齿根应力基本值的式（6-130）中的系数Y_Fa、Y_sa、Y_ε、Y_LS和Y_K，所以

Y_P的值用下式计算：

代入式（6-131）得

式中 Y_A——B2法的锥齿轮校正系数，用于一般的渗碳和表面淬火的锥齿轮；

Y_J——B2法的弯曲强度几何系数。

弯曲强度几何系数Y_J考虑了以下因素的影响：齿形、最大的破坏载荷作用的位置、由于齿根几何形状引起的应力集中、相啮合齿轮副中相邻齿间的载荷分配、相啮合的大小齿轮间齿厚的比、齿长方向修形后的有效齿宽、一对齿轮副中一个齿轮延长齿宽引起的影响，以及包括了作用在轮齿上载荷的切向（弯曲）和径向（压缩）分力的作用。

2）许用齿根应力 大小齿轮的许用齿根应力σ_FP要分别计算，要根据实际齿轮的几何相似性、运转状况和制造情况进行计算。

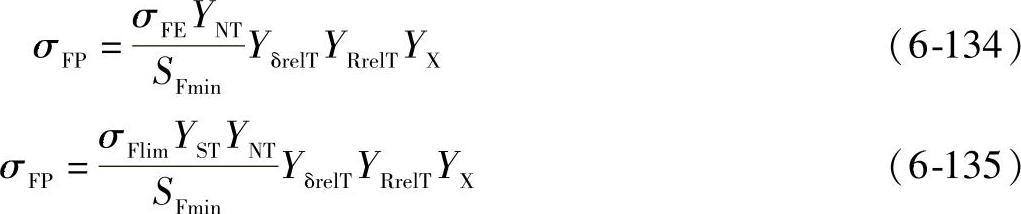
式中 σ_FE——包括了应力修正系数的弯曲疲劳极限，σ_FE=σ_FlimY_ST，假设材料（包括热处理）在全弹性状态下，无缺口试件的基本弯曲强度；

σ_Flim——由试验齿轮的弯曲疲劳极限，其值与试验齿轮的材料、热处理、齿根圆角的几何尺寸有关；

Y_ST——应力修正系数，与试验齿轮的尺寸有关，Y_ST=2.0；

S_Fmin——最小安全系数；

Y_δrelT——相对齿根圆角敏感系数，是考虑计算齿轮齿根圆角敏感系数与试验齿轮的不同对许用应力值的影响（Y_δrelT=Y_δ/Y_δT考虑材料对圆角的敏感性）；

Y_RrelT——相对齿根表面状况系数（Y_RrelT=Y_R/Y_RT考虑齿根圆角状况与试验齿根状况的关系）；

Y_X——齿根强度的尺寸系数，是考虑模数对齿根强度的影响；

Y_NT——寿命系数，考虑齿轮运转循环次数的影响。

大小齿轮的弯曲强度的计算安全系数要分别计算，根据许用齿根应力值用下式计算：

注；这是与传递的转矩有关的计算安全系数。

关于安全系数和失效概率见本章8.3.1节。

（3）齿形系数Y_Fa和应力修正系数Y_sa———B1法

齿形系数Y_Fa是考虑作用在齿顶时齿形对齿根名义弯曲应力的影响，大小齿轮的齿形系数要分别计算。

一般锥齿轮是啮合线为“8”字形的齿廓，并进行齿顶和齿根修缘，虽然与渐开线齿廓有些偏差，由于齿根修缘使弯矩力臂稍减小，所以在计算齿形系数时可以忽略上述的偏差。

把当量圆柱齿轮齿廓齿根处30°切点间的距离作为危险截面弦齿厚（见图6-59）。

本部分的Y_Fa和Y_sa是按没有公差的名义齿轮计算的，由于轮齿侧隙使齿厚稍微减小，在承载能力计算时可以忽略。但是，当齿厚减薄量A_sne>0.05m_mn时，应当考虑尺寸的减小。

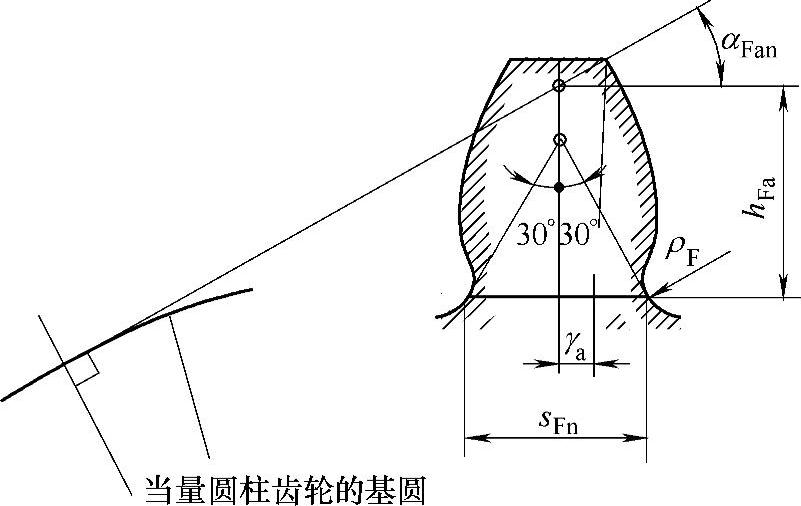
图6-59 当量圆柱齿轮的齿根危险截面弦齿厚s_Fn，载荷作用于齿顶时的弯曲力臂h_Fa

1）展成法加工齿轮的齿形系数Y_Fa式（6-137）用于在法截面内有或没有齿廓变位的当量圆柱齿轮，变位并满足下列假设条件：

a）30°切线切点位于用有齿顶圆角半径的刀具展成的齿根曲线上。

b）加工用的刀具带有一定的齿顶圆角半径（ρ_a0≠0）。

式中代号意义见图6-59，关于轮齿的名义载荷和齿形系数的叙述见GB/T 3480—1997。

①辅助值。为了计算齿根危险截面弦齿厚s_Fn和弯曲力臂h_Fa，首先要确定辅助值E、G、H和θ：

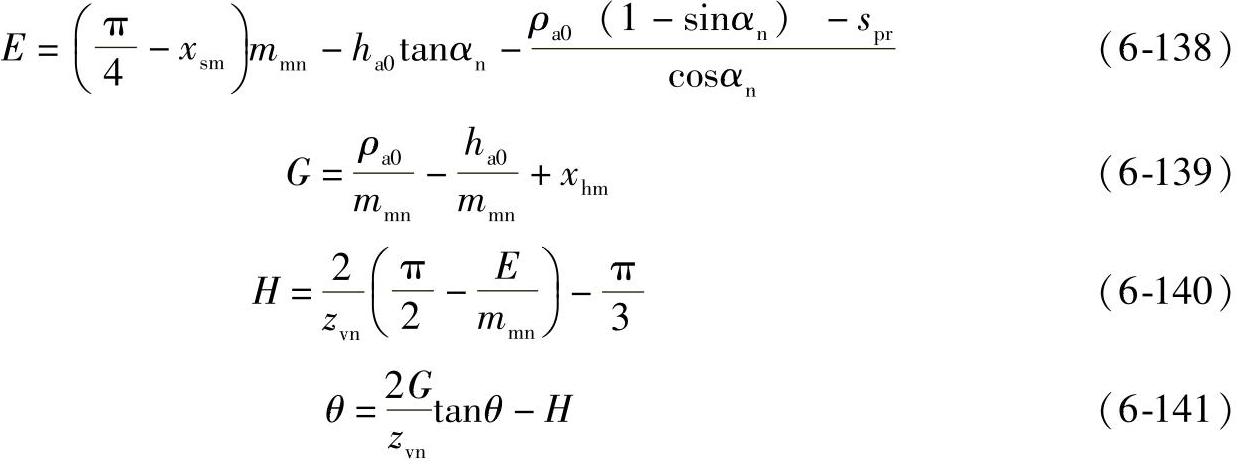
为了解超越方程式（6-141），可取初始值θ=π，在大多数情况下，迭代几次，该方程就收敛了。

②齿根危险截面弦齿厚s_Fn

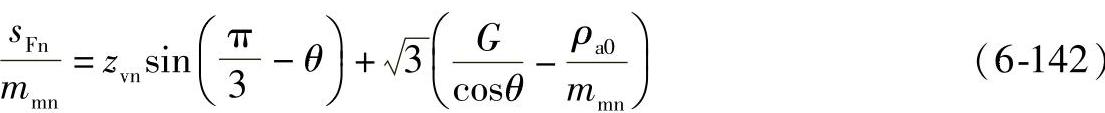
③危险截面处齿根圆角半径ρ_F

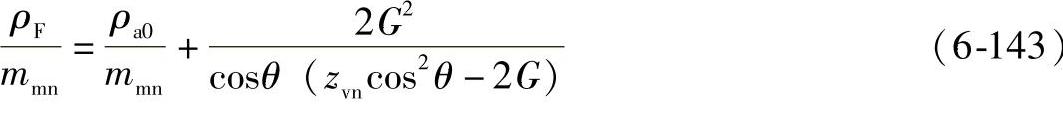
④弯曲力臂h_Fa

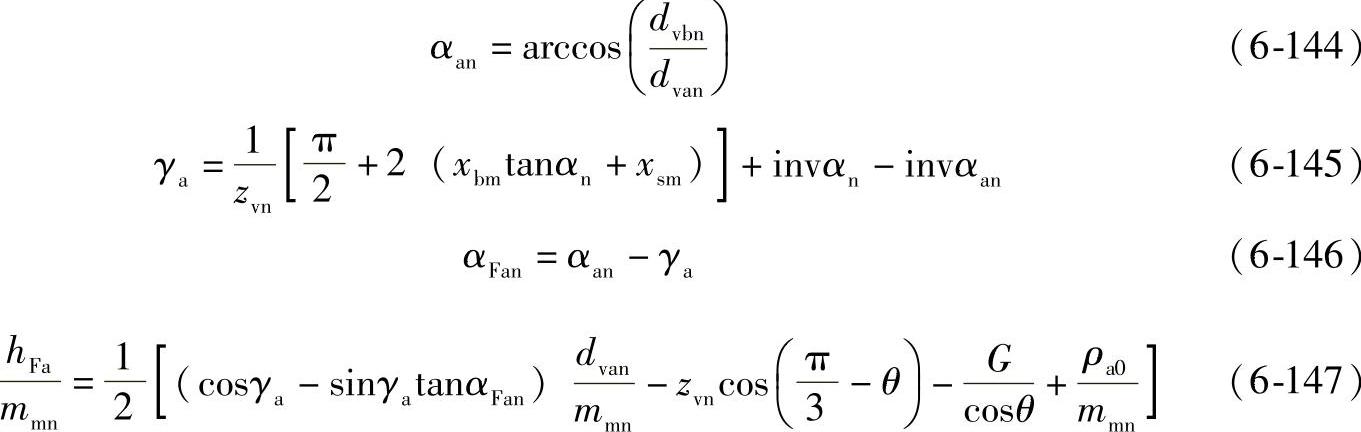
在法截面内，当量圆柱齿轮参数见本章8.3.1节（7）。刀具轮齿基本齿条齿廓的尺寸图6-60。对于刀具基本齿廓为α_n=20°、h_a0/m_mn=1.25、ρ_a0/m_mn=0.25、x_sm=0的齿轮，其齿形系数可从图6-61查得。其他的刀具基本齿廓参数见GB/T 3480—1997。

对于展成锥齿轮的复合齿形系数Y_FS=Y_FaY_sa，见图6-62～图6-64。

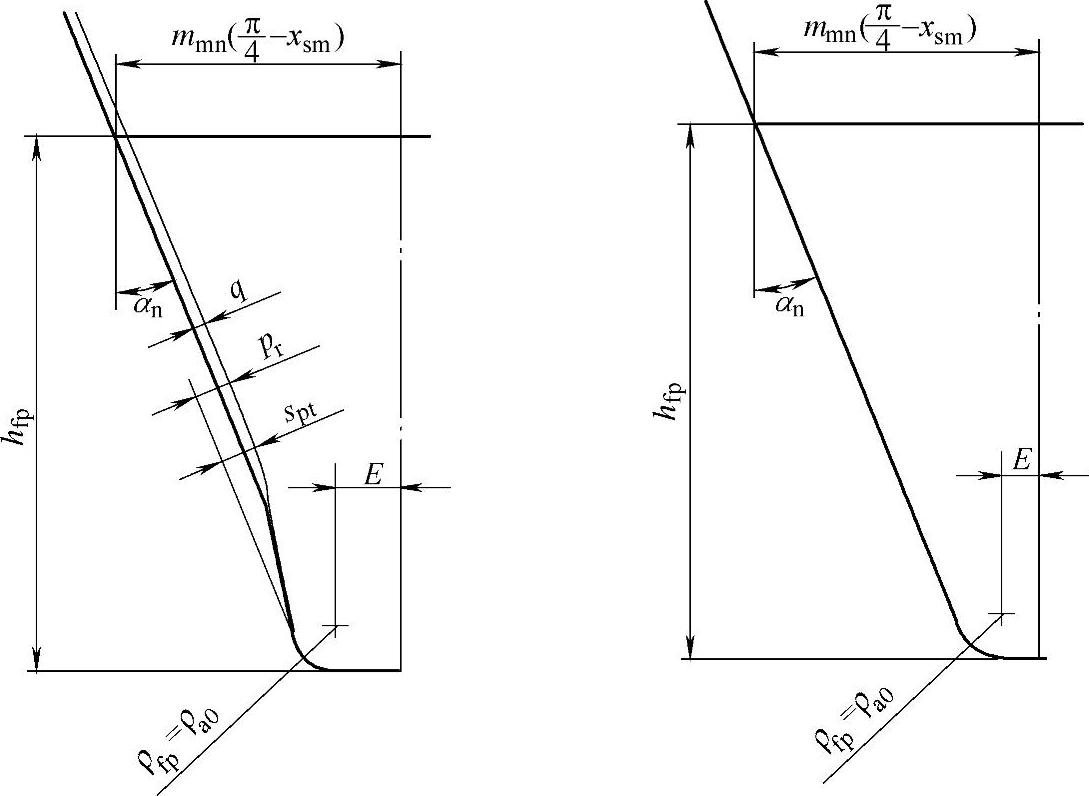
图6-60 刀具基本齿条齿廓尺寸

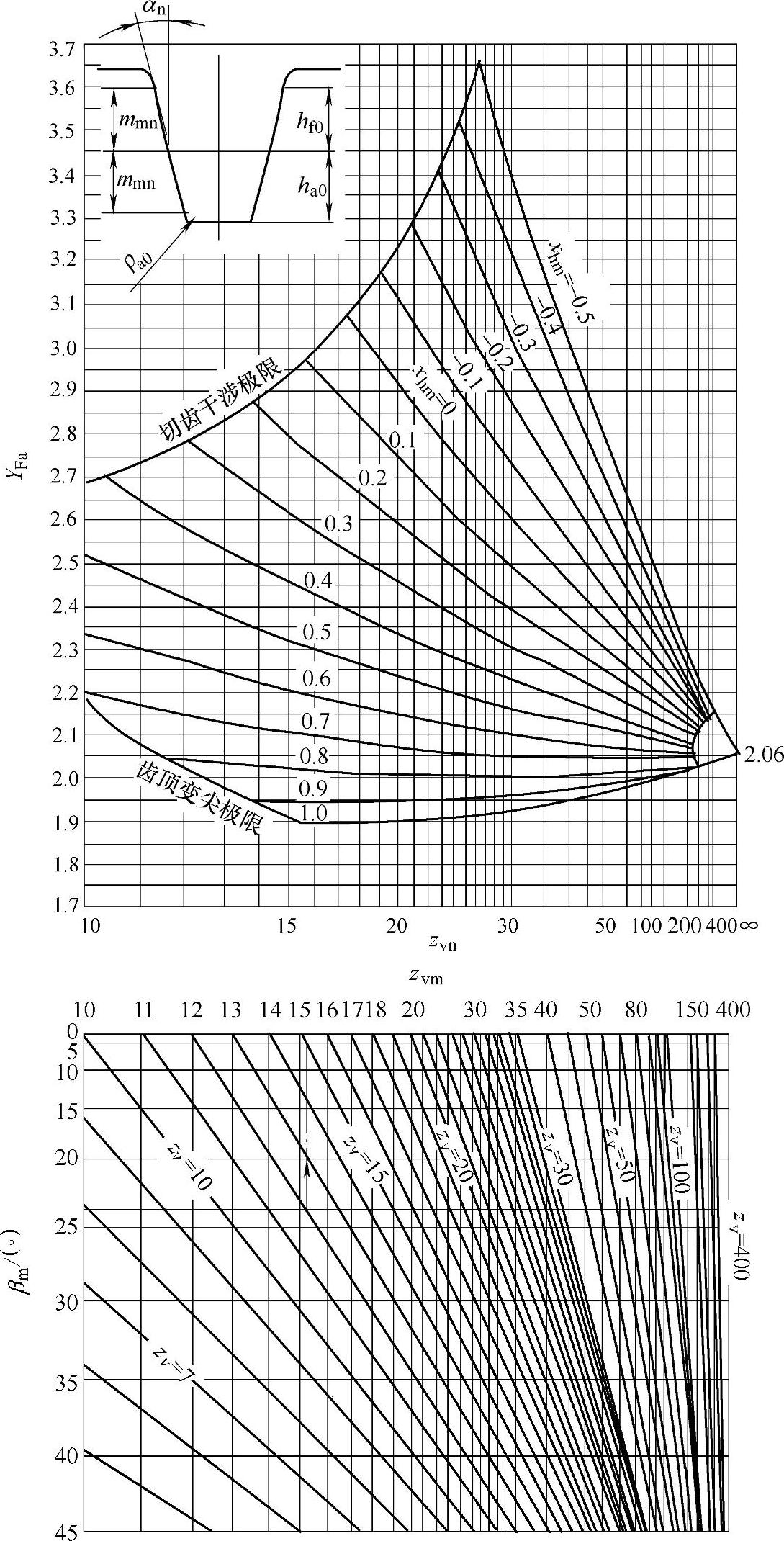
图6-61 展成齿轮的齿形系数Y_Fa

例：由β_m=23.5，z_v=12得z_vn=15.2。

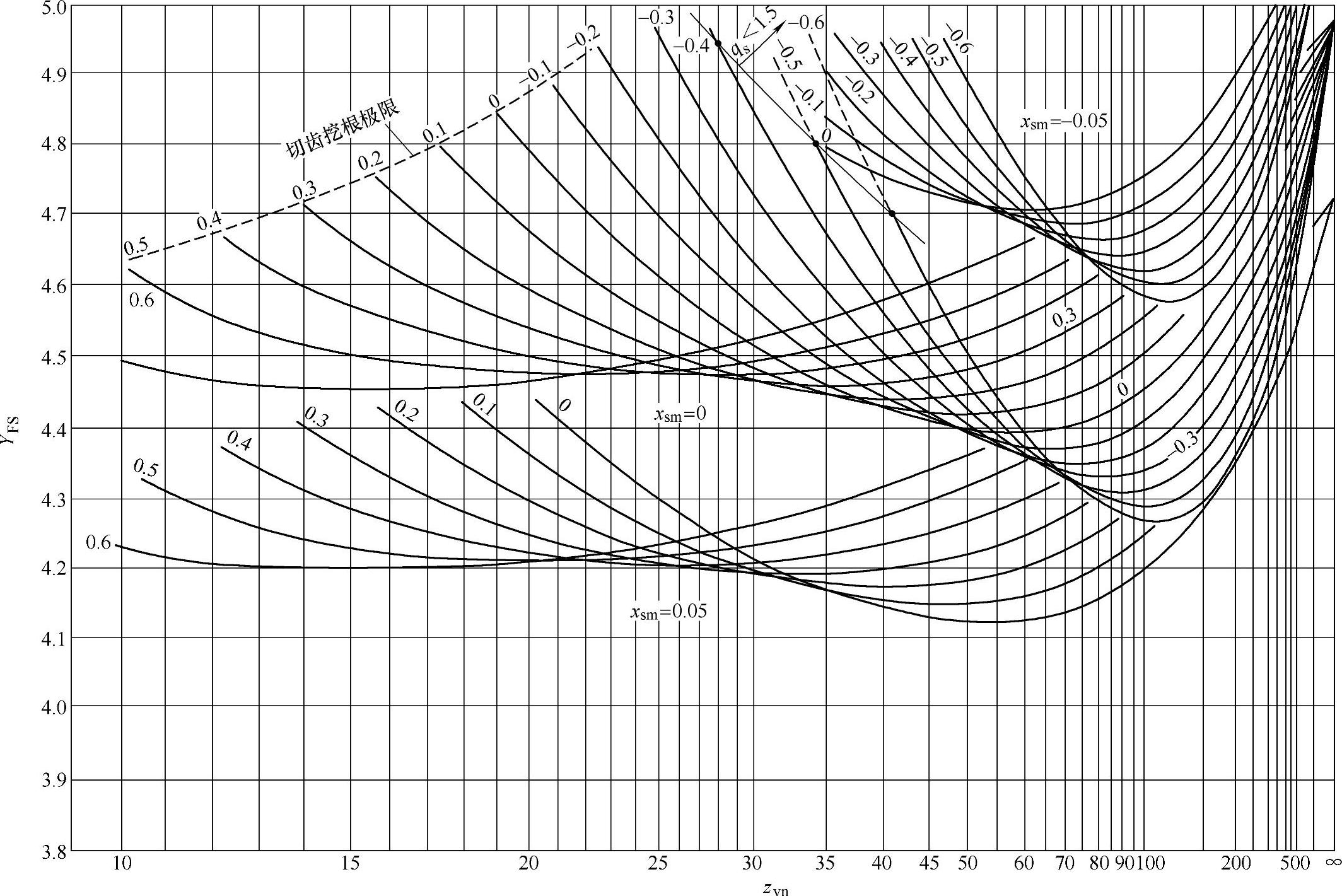
图6-62 展成齿轮的复合齿形系数Y_FS=Y_FaY_Sa（ρ_aO=O.2m_mn）

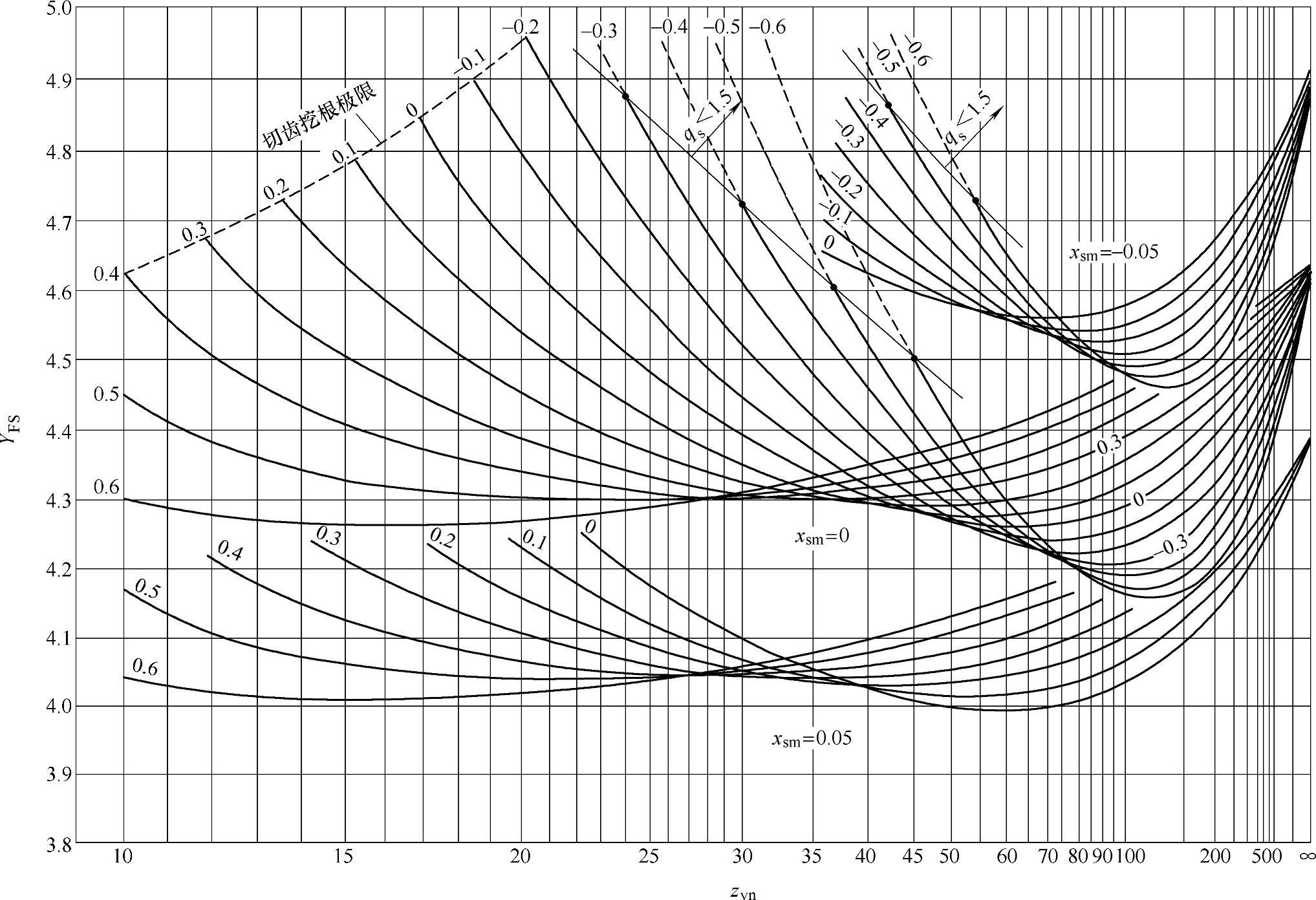
图6-63 展成齿轮的复合齿形系数Y_FS=Y_FaY_Sa（ρ_aO=O.25m_mn）

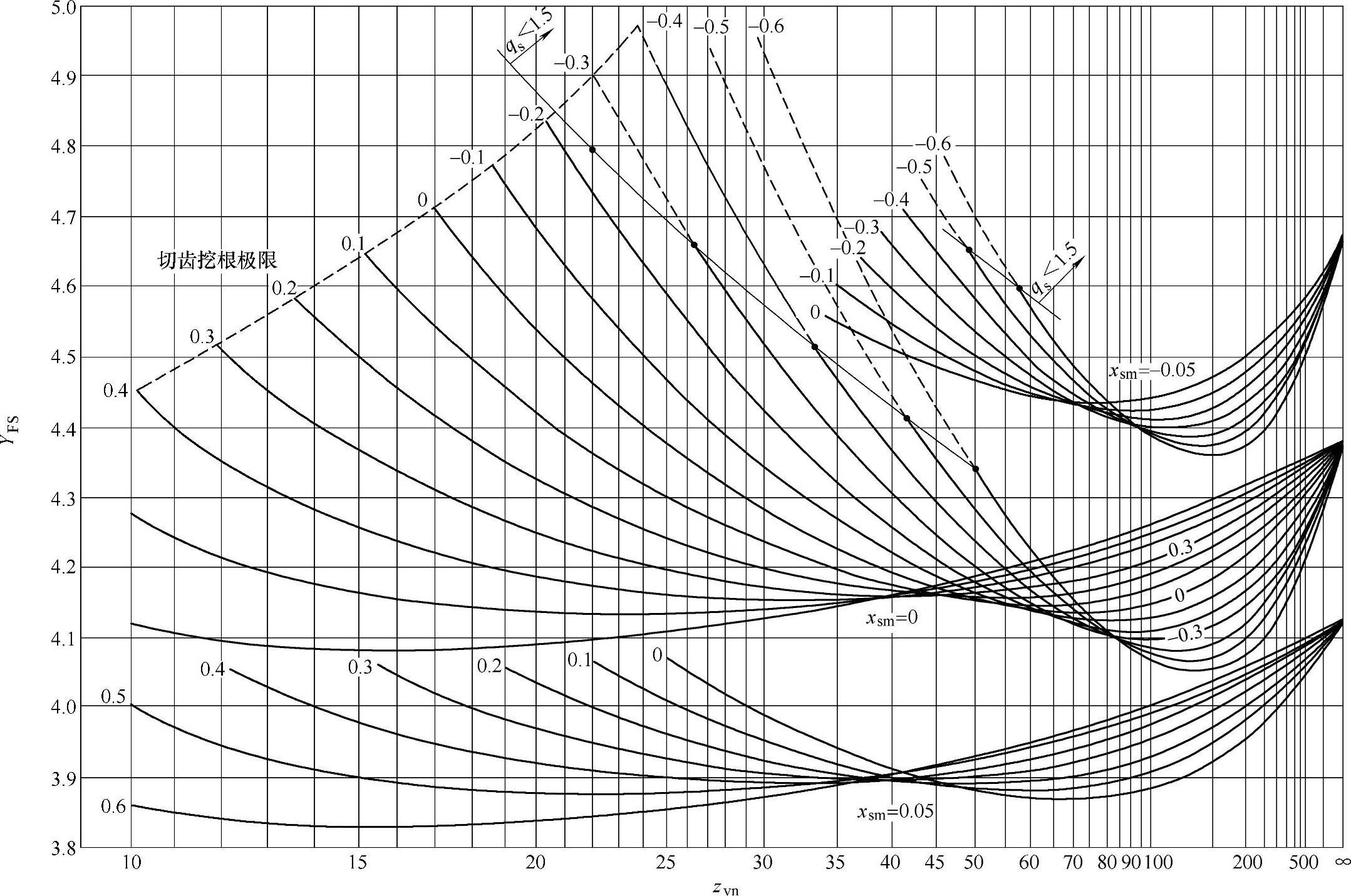
图6-64 展成齿轮的复合齿形系数Y_FS=Y_FaY_Sa（ρ_a0=0.3m_mn）

2）成形法加工的齿轮的齿形系数Y_Fa有的鼓形齿轮可用成形法切削加工（特别在大的齿数比时），所测齿轮齿槽齿廓和刀具齿廓（齿条刀具齿廓）一致，鼓形齿轮的齿形系数可直接按刀具齿廓确定。

危险截面弦齿厚：

s_Fn2=πm_mn^-2E-2ρ_a0.2cos30° （6-148）

式中E按式（6-138）计算。

在30°切线切点处的曲率半径：

ρ_F2=ρ_a02 （6-149）

弯曲力臂：

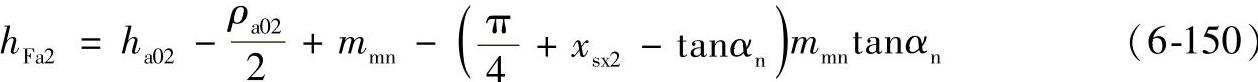
齿形系数按式（6-137）计算，并取α_Fan=α_n：

在大轮齿数比u>3时，与其相啮合的小锥齿轮是用展成法加工的，小锥齿轮的齿形系数可近似地按展成法中的方法计算。

3）应力修正系数Y_sa应力修正系数Y_sa是把名义弯曲应力转换成齿根应力基本值的系数。它考虑了齿根过渡曲线处的应力集中的效应，以及弯曲应力以外的其他应力对齿根应力的影响（进一步的说明见GB/T 3480—1997）。

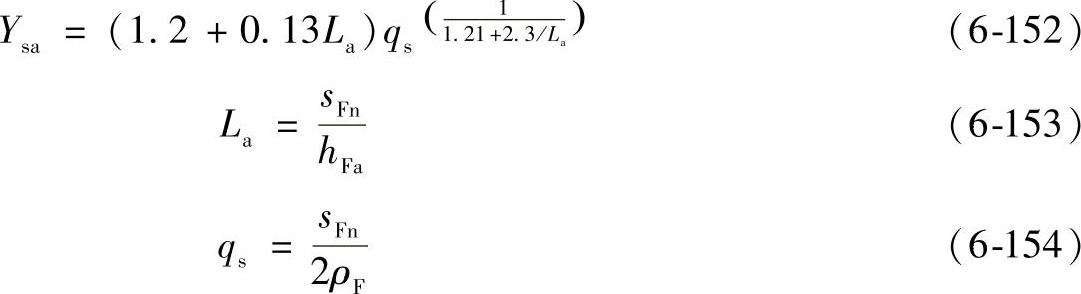
式中 s_Fn——分别按式（6-142）或式（6-148）计算；

h_Fa——分别按式（6-147）或式（6-150）计算；

ρ_F——分别按式（6-143）或式（6-149）计算。

式（6-152）的有效范围是1≤q_s<8。

对于刀具基本齿廓为α_n=20°、h_a0/m_mn=1.25、ρ_a0/m_mn=0.25和x_sm=0的齿轮，应力修正系数Y_sa可从图6-65查得。关于磨削台阶的影响见GB/T 3480—1997。

（4）重合度系数Y_ε，锥齿轮系数Y_K，载荷分担系数Y_LS———B1法

1）重合度系数Y_ε重合度系数Y_ε是把作用在齿顶的载荷（此处用齿形系数Y_Fa和应力修正系数Y_sa）转换到指定的点的系数。

Y_ε也可用端面载荷分配系数K_Fα计算：

当ε_Vβ=0时：

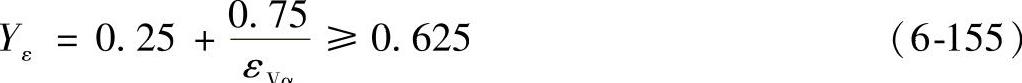
当0＜ε_Vβ≤1时：

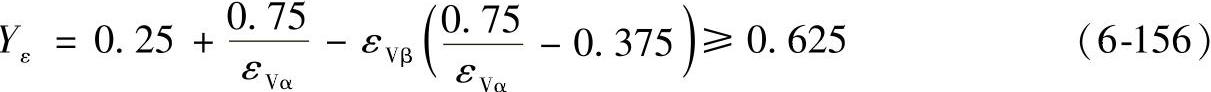
当ε_Vβ＞1时：

Y_ε=0.625 （6-157）

2）锥齿轮系数Y_K锥齿轮系数Y_K是考虑锥齿轮与圆柱齿轮的差异对齿根应力影响的系数（因接触线倾斜，l_bm′的值较小）。

式中 l_bm′——中部接触线的投影长度[见式（6-86）]。

3）载荷分担系数Y_LS载荷分担系数Y_LS是考虑两对轮齿或多对轮齿间的载荷分配的系数。

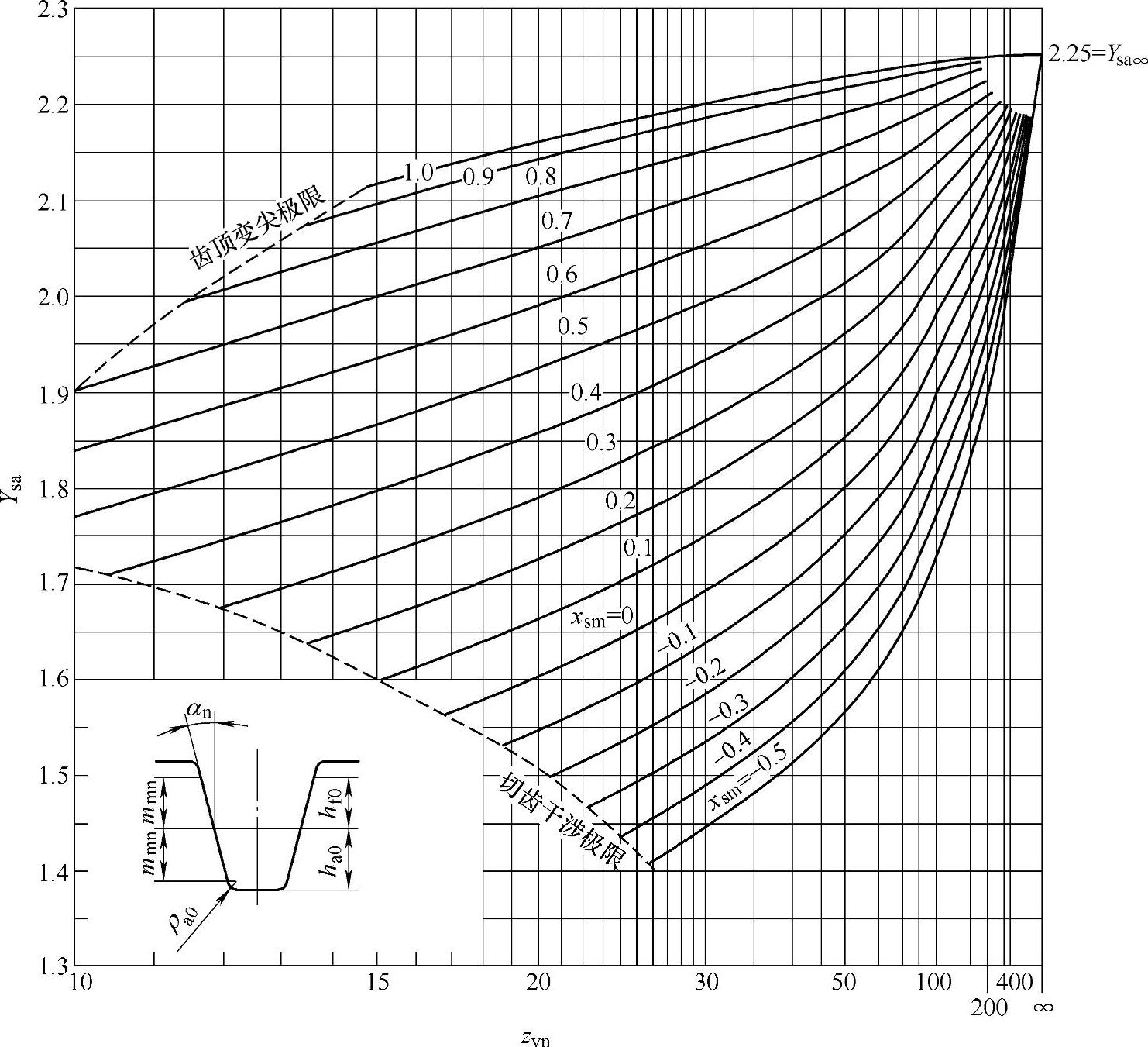
图6-65 载荷作用在齿顶时的应力修正系数Ysa

Y_LS=Z²_LS （6-159）

（5）弯曲强度计算的复合几何系数Y_P——B2法

1）曲线图和概述 图6-70～图6-81包含有直齿锥齿轮、零度齿锥齿轮和弧齿锥齿轮几何系数的曲线图，图中曲线是按齿宽b=0.3R_e和b=10m_et中的较小者确定的。当设计齿轮的齿形各部分尺寸和齿厚、齿宽、刀刃的半径、压力角、螺旋角、并用凹侧为主动侧等与曲线图中参数相符合时，可利用这些曲线图。

不能应用这些曲线图时，可用下面的公式计算，由于计算复杂，建议用计算机计算。

2）锥齿轮几何系数Y_J的计算公式 锥齿轮几何系数Y_J可用下式计算：

式中 Y_K1，2——齿形系数，包含了小轮或大轮的应力集中系数；

ε_N——载荷分配率；

Y_i——惯性系数，用于重合度较小的齿轮；

r_my01，2——小轮或大轮上载荷作用点的平均端面半径（mm）；

b_ce1，2——小轮或大轮的计算的有效齿宽（mm）。

3）最大弯曲应力时载荷的作用点y₃对于大多数的直齿锥齿轮、零度齿锥齿轮和弧齿锥齿轮，当总重合度≤2时，载荷作用在当量圆柱齿轮的单对齿啮合区外界点时，产生最大弯曲应力；当总重合度>2时，假设接触线经过啮合轨迹的中心时，产生最大弯曲应力；对于承受静载荷的直齿锥齿轮和零度齿锥齿轮（例如汽车的差速器中用这些齿轮），载荷作用在齿顶处，产生最大弯曲应力。在以上几种情况下，从接触区的中点沿啮合轨迹到载荷作用点的测量值定义为y_J，从接触起始点到载荷作用点的距离定义为y₃。

当ε_vγ≤2时

及g²_η=g²_vancos²β_vb+b²sin²β_vb （6-162）

当ε_vγ＞2时

y_J=0 （6-163）

当直齿锥齿轮和零度齿锥齿轮承受静载荷时

对于直齿锥齿轮和零度齿锥齿轮

对于弧齿锥齿轮

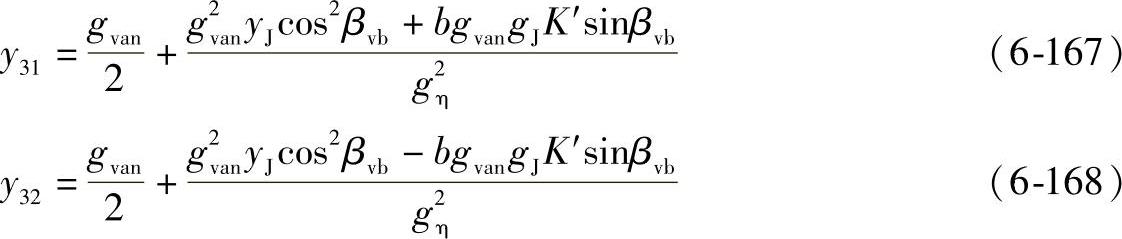
式中 K′——位置常数。

4）载荷作用点半径r_my01，2因为载荷作用点的位置通常不在轮齿中点截面上，实际的半径用下列公式确定：

对于直齿锥齿轮和零度齿锥齿轮

对于弧齿锥齿轮

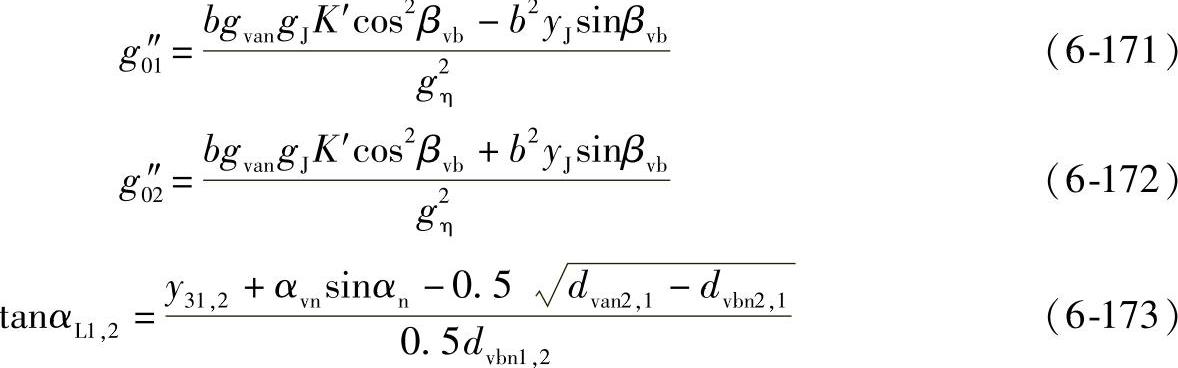
式中 α_L1，2——在小轮或大轮上载荷作用点的名义压力角：

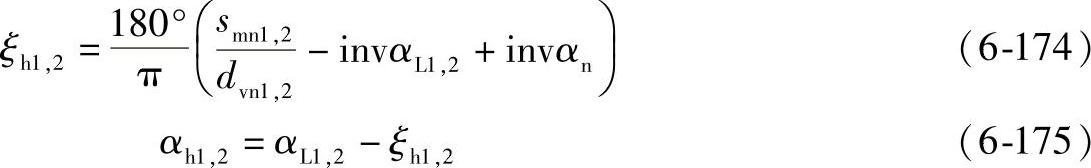
式中 ξ_h1，2——小轮或大轮弯曲强度计算中用的转角。

在小轮或大轮轮齿中心线上，从节圆到载荷作用点的距离。

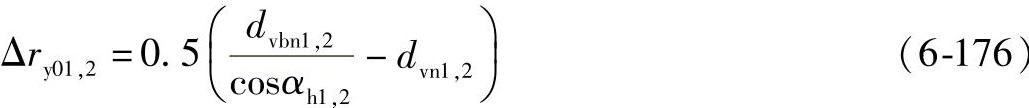
载荷作用点的端面半径：

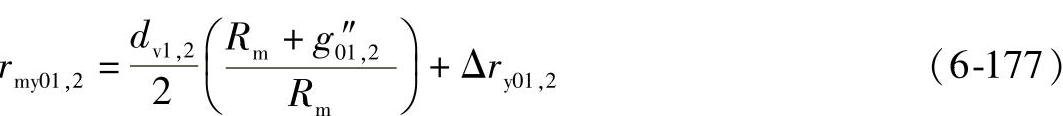
5）齿根圆角半径r_mf最小的齿根圆角半径在齿根圆角与齿根圆相切处，其半径可用下式计算：

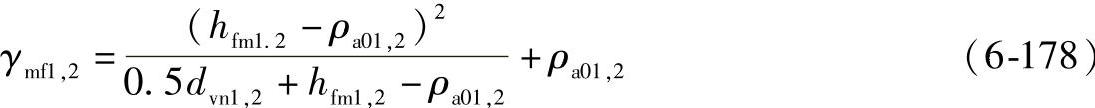
6）齿形系数Y₁和Y₂这个齿形系数把名义载荷的径向分量和切向分量合并在一起；因为这个系数必须按最薄弱的截面确定，最薄弱截面必须用迭代法确定，小轮和大轮要分别计算。

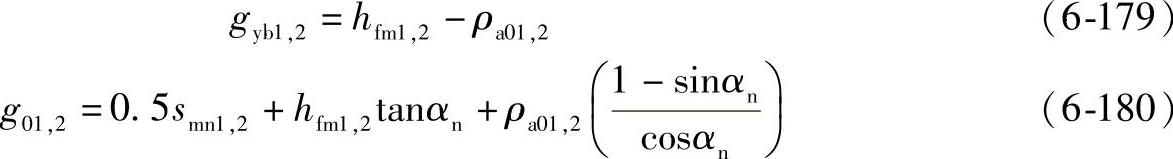
式中 g₀₁，2——计算的值。

取一个初始值，使g_f01，2（1）=g₀₁，2+g_y01，2

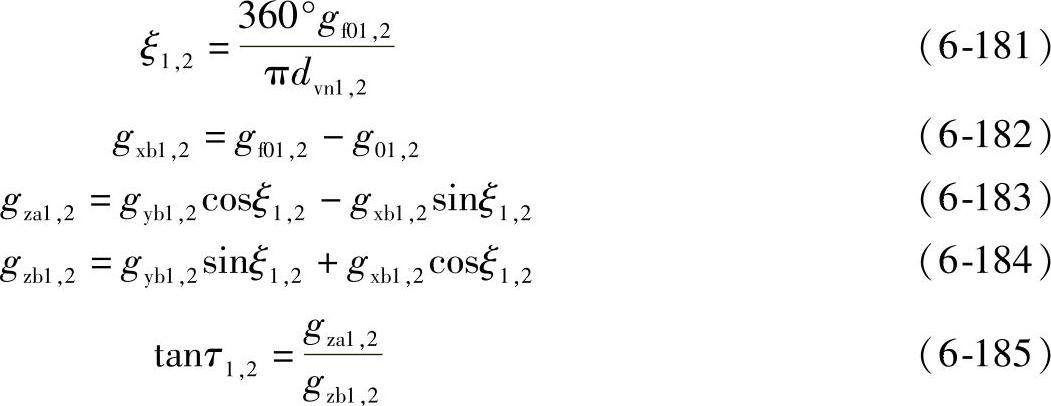
sN1，2=0.5dvn1，2 sinξ1，2-ρa01，2 cosτ1，2-gzb1，2 （6-186）

h_N1，2=Δr_y01，2^+0.5d_vn1，2（1^-cosξ₁，2）+ρ_a01，2 sinτ₁，2+g_za1，2 （6-187）

改变g_f01，2值重复上面计算，直到：

第二步试凑，使g_f01，2（2）=g_f01，2（1）+0.005m_et。

第三步试凑和继续试凑，并进行插值。

轮齿强度系数x_N1，2

齿形系数：

7）应力集中和应力修正系数Y_f应力集中和应力修正系数Y_f与下列因素有关：

a）有效的应力集中。

b）载荷的作用位置。

c）材料可塑性的影响。

d）残余应力的影响。

e）材料成分的影响。

f）由于齿轮制造和以后的工作引起的齿面粗糙度。(www.daowen.com)

g）赫兹应力的影响。

h）尺寸的影响。

i）齿端的影响。

下面的应力集中和应力修正系数是道兰（Dolan）和布朗格哈默（Broghamer）推导的，仅考虑了a）和b）两个因素。

式中

L=0.3254545-0.0072727α_n

M=0.3318182-0.0090909α_n

O=0.2681818-0.0090909α_n

从a）～i）的其他因素可用式（6-130）补偿，通常d）和e）包括在许用齿根应力值σ_FP中，h）在尺寸系数Y_X中考虑，i）在计算的有效齿宽b_ce中考虑。

8）包含应力集中的修正齿形系数Y_K这个系数仅仅是把齿形系数Y₁，2、应力集中和应力修正系数Y_f1，2相组合起来。

9）载荷分配率ε_N载荷分配率ε_N用于计算总载荷作用在所分析轮齿上的比例，可用下列公式计算：

式（6-193）中k是从1到x或y的连续正整数，该数使每个根式中产生实项（即根式中为正值），应当忽略虚项（即根式中为负值）。

对于大多数的设计，x和y不大于2。

对于承受静载荷的直齿锥齿轮和零度齿锥齿轮：

ε_N=1.0 （6-195）

10）惯性系数Y_i惯性系数Y_i是考虑动载荷作用在重合度较小的齿轮上时轮齿啮

合的不均匀性的系数，该系数可用下式计算：

当ε_vγ＜2.0时

其他情况时

对于承受静载荷的齿轮，例如车辆驱动差速齿轮，甚至ε_vγ＜2.0时，Y_i=1.0。

11）计算的有效齿宽b_ce因为瞬时接触线常常不是全齿宽接触，这个量是评定轮齿承受的载荷在齿根截面上分布的有效性。有效齿宽用下式计算：

式中 g_k——瞬时接触线在齿长方向投影的长度（mm）。

轮齿小端增量

轮齿大端增量

当Δb_i′₁，2和Δb_e′₁，2均为正值时

Δb_i1，2=Δb_i′₁，2

当Δb_i′₁，2为正值和Δb_e′₁，2为负值时

当Δb_i′₁，2为负值和Δb_e′₁，2为正值时

Δb_i1，2=0

当Δb_e′₁，2和Δb_i′₁，2均为正值时

Δb_e1，2=Δb_e′₁，2

当Δb_e′₁，2为正值和Δb_i′₁，2为负值时

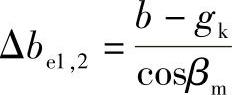
当Δb_e′₁，2为负值和Δb_i′₁，2为正值时

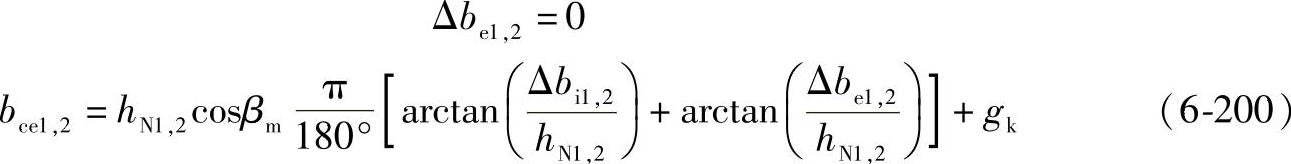
式中 b_ce1，2——计算的有效齿宽（mm）。

（6）相对齿根圆角敏感系数Y_δrelT

动态的齿根圆角敏感系数Y_δ，表示疲劳损坏时理论的应力峰值超过材料弯曲疲劳根限的程度，它是材料和应力梯度的函数。敏感系数可根据无缺口和有缺口的试件或试验齿轮经试验得到的强度值计算得到。如果没有较精确的试验结果（A法），Y_δrelT可用下面叙述的方法确定。

1）B1法 锥齿轮（和其当量圆柱齿轮）的许用齿根应力是根据圆锥和圆柱试验齿轮的疲劳强度确定的，所以相对齿根圆角敏感系数Y_δrelT=Y_δ/Y_δT可直接从图6-66查得，它是所计算齿轮的q_s和材料的函数。

计算相对齿根圆角敏感系数Y_δrelT可用下式计算，该式表示图6-66中的曲线。

X^*_T=1.2及q_sT=2.5

式中 ρ′——滑移层厚度，ρ′是材料的函数，可从表6-35查得；

X^*——适用于模数m_mn=5mm，其尺寸的影响用Y_X考虑。

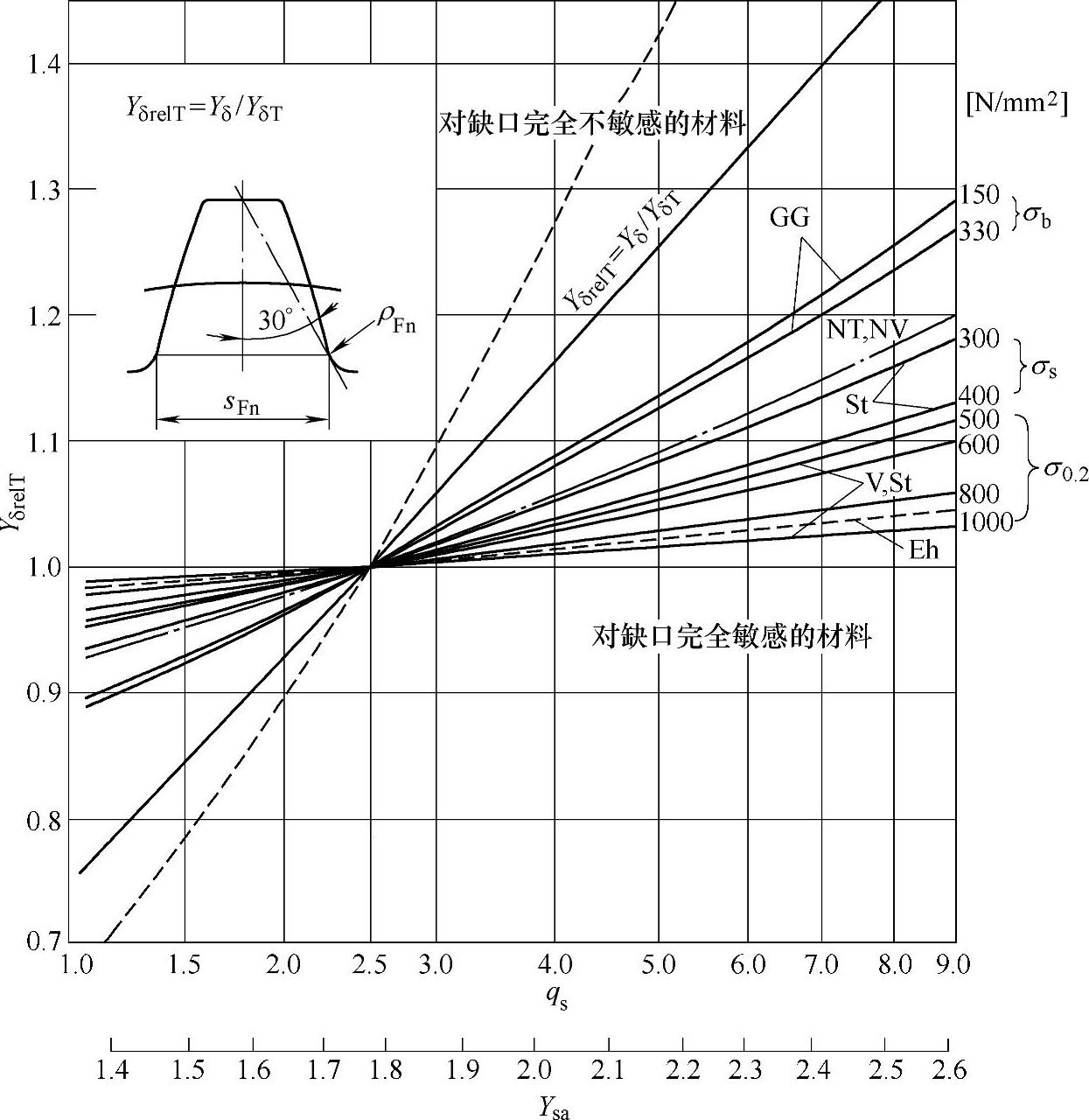
图6-66 与标准试验齿轮尺寸相关的相对齿根圆角敏感系数（许用齿根应力按名义弯曲应力确定）

表6 - 35 滑移层厚度ρ′

2）B2法 一般这个方法对于工业齿轮足够精确，当齿轮q_s≥1.5时，可取：

Y_δrelT=1.0 （6-202）

对于q_s＞2.5，取上面的值偏于安全。

当q_s＜1.5时，考虑许用齿根应力将减小，可取：

Y_δrelT=0.95（6-203）

在图6-62～图6-64中给出q_s=1.5的根限曲线。

（7）相对齿根表面状况系数Y_RrelT

相对表面状况系数Y_RrelT是考虑齿根表面状况（主要取决于齿根圆角处的表面粗糙度）相对于Rz=10μm的标准齿轮（见GB/T 3480—1997）齿根表面状况，对齿根强度的影响。

如果通过对所有因素进行更精确的分析来确定齿根表面状况系数无法实现时（A法），可用下面所叙述的方法确定。

注意：在齿根表面没有深度大于2Rz的擦伤或类似的缺陷时，这些方法才有效。

1）B1法 相对齿根表面状况系数Y_RrelT可按粗糙度和材料从图6-67查得，图中曲线是用试件做试验得到的；也可用式（6-204）～式（6-209）计算。

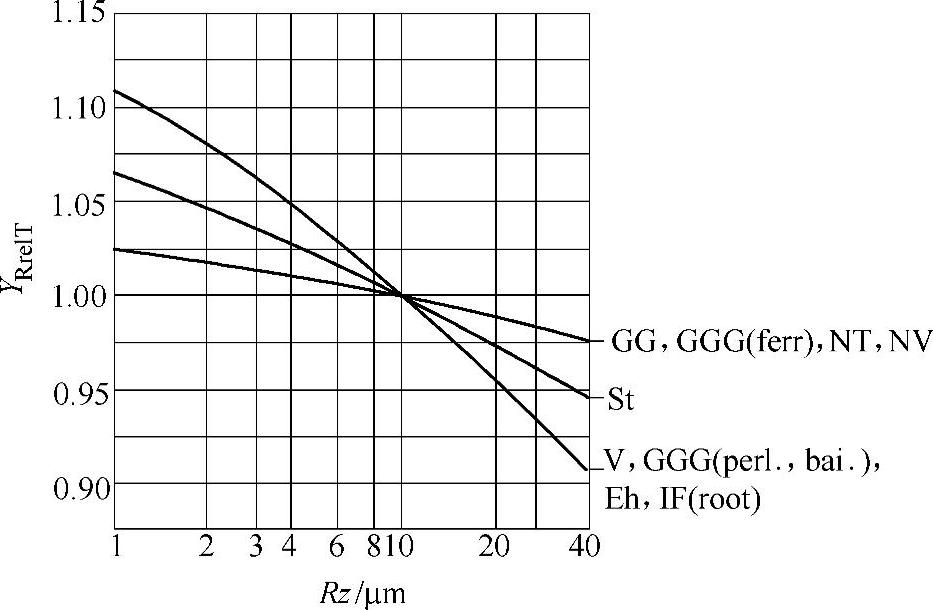
图6-67 相对齿根表面状况系数Y_RrelT，用于确定与试验齿轮尺寸相关的许用齿根应力

当Rz<1μm时：

对于调质钢和渗碳钢

Y_RrelT=1.12 （6-204）

对于结构钢

Y_RrelT=1.07 （6-205）

对于灰铸铁、渗氮钢、氮碳共渗钢

Y_RrelT=1.025 （6-206）

当1μm≤Rz≤40μm时：

对于调质钢和渗碳钢

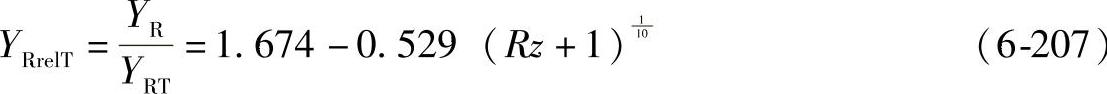
对于结构钢

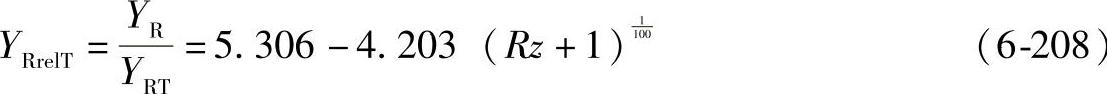
对于灰铸铁、渗氮钢、氮碳共渗钢

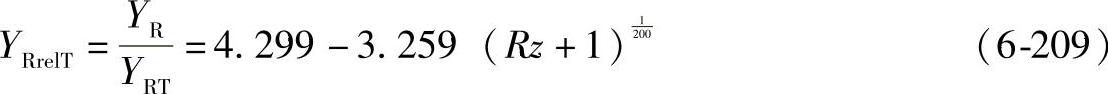
2）B2法 齿轮的齿根表面粗糙度Rz≤16μm时，一般可取

Y_RrelT=1.0 （6-209a）

由图6-67可知，当10μm<Rz≤16μm时，材料弯曲疲劳极限稍偏小；当Rz<10μm时，按式（6-209a）的计算偏于安全。

（8）尺寸系数Y_X

尺寸系数Y_X是考虑强度随着尺寸的增大而减小的系数。

对Y_X影响的主要因素有：

——轮齿尺寸；

——齿轮直径；

——轮齿尺寸与直径之比；

——接触斑点的面积；

——材料和热处理；

——渗碳深度与齿厚之比。

如果没有个人的或其他验证过的经验，Y_X可按法向模数m_mn和材料近似地从图6-68查取。

Y_X可用式（6-210）～式（6-212）计算，近似地表示图6-68中的曲线。

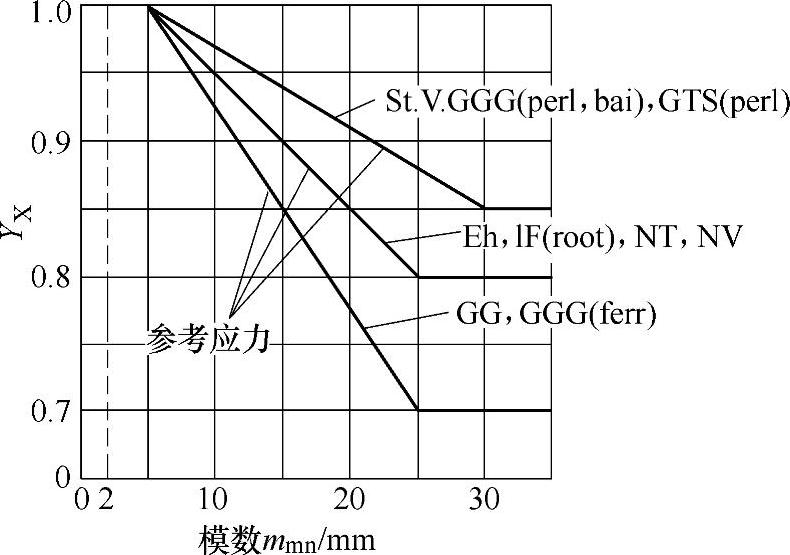
图6-68 弯曲强度的尺寸系数Y_X（用于材料弯曲疲劳极限）

1）结构钢、调质钢、球墨铸铁、珠光体可锻铸铁

Y_X=1.03-0.006m_mn （6-210）

并规定0.85≤Y_X≤1.0。

2）渗碳淬火钢、全齿廓感应或火焰淬火钢、渗氮钢或氮碳共渗钢

Y_X=1.05-0.01m_mn （6-211）

并规定0.8≤Y_X≤1.0。

3）灰铸铁

Y_X=1.075-0.015m_mn （6-212）

并规定0.70≤Y_X≤1。

（9）寿命系数Y_NT

寿命系数Y_NT是有限寿命（应力循环次数有限）时所允许比较高的弯曲应力与在3×10⁶循次数的弯曲疲劳极限应力的比值。

对Y_NT的主要影响因素有：

——材料和热处理（见GB/T 3480.5—2008）；

——载荷的循环次数（使用寿命）N_L；

——失效判据；

——要求的运转平稳性；

——齿轮材料的纯度；

——材料的塑性和断裂韧性；

——残余应力。

应力循环次数N_L的定义为在载荷作用下轮齿啮合的次数。材料的弯曲疲劳极限是按轮齿加载循环次数3×10⁶建立的，可靠度99%。

超过3×10⁶循环次数，经验证明可取Y_NT=1。

当Y_NT=1时，应考虑采用最佳的材质和制造工艺。

1）A法（Y_NT-A）S-N或损伤曲线是从实际齿轮在有限寿命下得到的曲线。在这种情况下，Y_δrelT、Y_RrelT和YX系数实际上已包括在S^-N/损伤曲线中，所以在计算用齿根应力时，可取Y_NT-A=1。

2）B法（Y_NT-B）这个方法是用标准试验齿轮的寿命系数Y_NT评估齿轮在有限寿命时的许用齿根应力和可靠性。Y_NT中没有包含Y_δrelT、Y_RrelT和Y_X的影响，因此在有限寿命时要考虑这些系数修正的影响。

①曲线图。对于静强度和疲劳强度，Y_NT值是材料和热处理的函数，Y_NT可从图6_-69查得；其值是根据大量试验得到的，其判据是：对于表面硬化钢和渗氮硬化钢是产生损伤或初始裂纹；对于结构钢和调质钢是达到屈服极限。

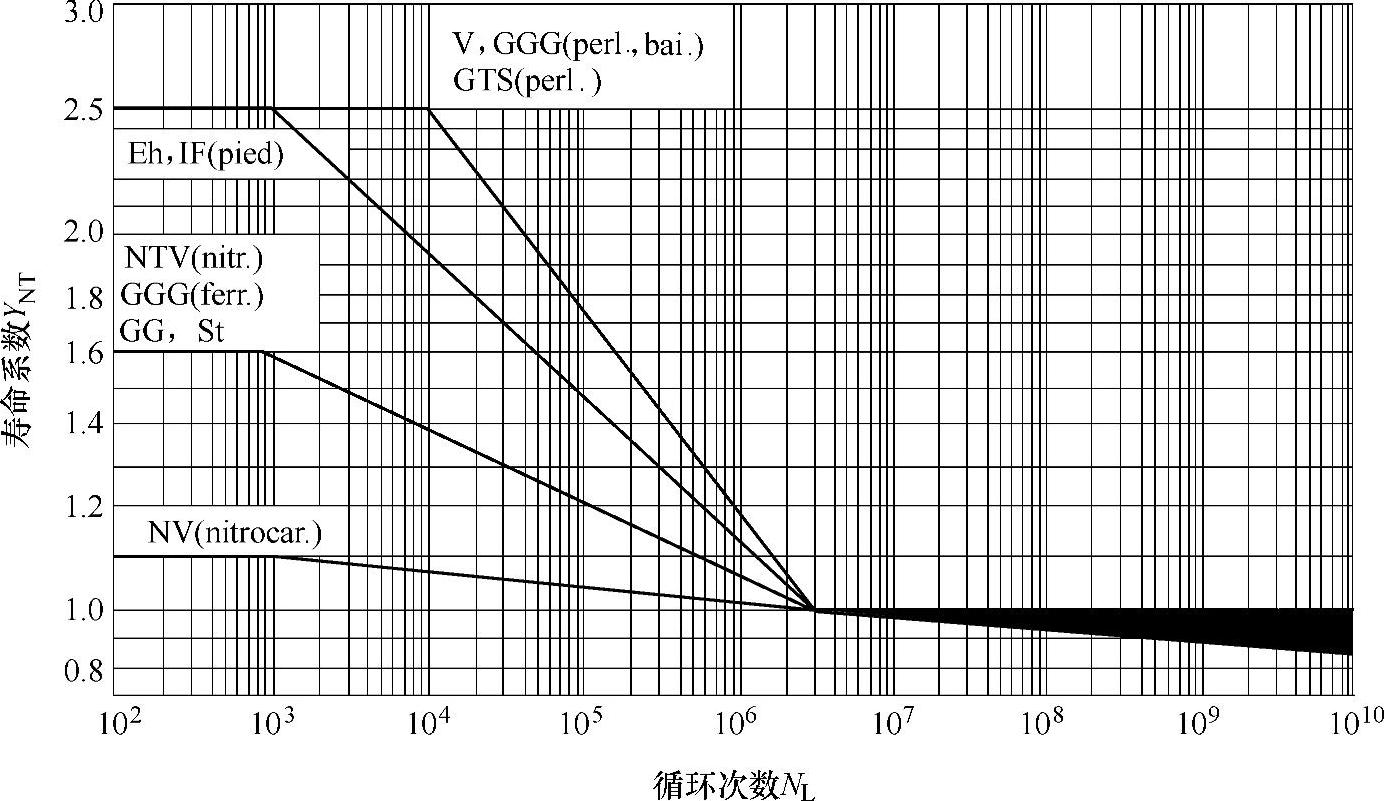
图6-69 寿命系数Y_NT（标准试验齿轮）

②计算法。对于静强度和疲劳强度的寿命系数可从表6-36查得，对于有限寿命的Y_NT在疲劳强度极限和静强度极限之间插值确定（Y_NT的插值计算见GB/T 3480—1997）。

注：对于循环次数≤10³，应避免应力水平高于允许值，否则轮齿材料会超过弹性极限。

表6-36 静强度和疲劳强度的寿命系数YNT

（10）锥齿轮的校正系数Y_A——B2法

锥齿轮的校正系数Y_A有两个作用，用这个系数把B2法的计算结果校正到B1法的计算结果，经校正后可利用GB/T 3480.5—2008中的试验齿轮的疲劳极限。

1）校正系数Y_A的初始值 可用初始值

Y_A1，2=1.2 （6-213）

这个值可用于m_mn=5mm，α_η=20°，β_m=35°，渗碳材料的齿轮。

2）校正系数Y_A的复合方程式B1和B2法间的主要区别是B2法中不仅包括弯曲应力，还包括了压缩应力[比较式（6-137）和式（6-190）]。可以为B2法的齿形系数与弯曲应力系数Y_B和压缩应力系数Y_C间的关系为：

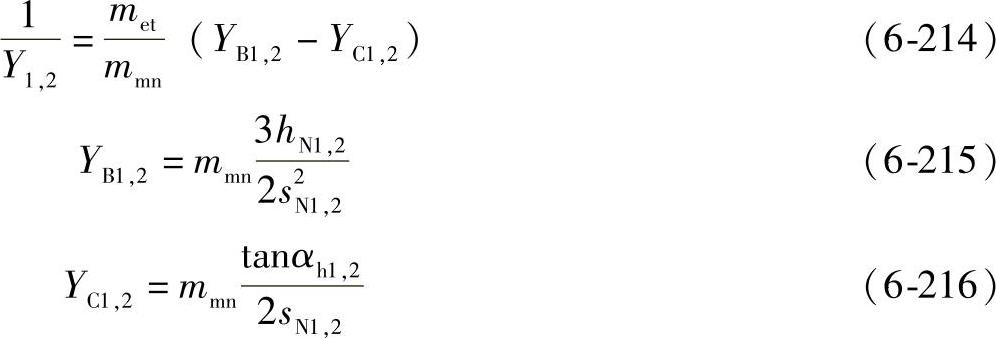
式中 Y₁，2——见式（6-190）；

h_N1，2——见式（6-187）；

s_N1，2——见式（6-186）；

α_h1，2——见式（6-175）。

认为cosα_Fan≈cosα_h≈cosα_n、h_Fa≈h_N^[2]和s_Fn≈2s_N，则

Y_B≈Y_FaY_ε （6-217）

式中 Y_Fa——见式（6-137）。

B1和B2法另一个区别是处理应力修正的方法不同[比较式（6-152）和（6-154）]。最近似的公式（包括了这两个方法的所有差异）为

比较B1和B2法得：

按照式（6-217）和式（6-218）的假设，得：

所以，校正系数Y_A为

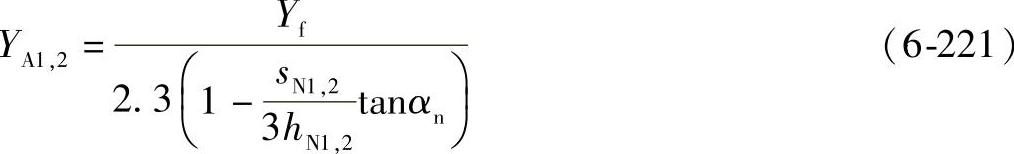
（11）几何系数曲线图——B2法（见图6-70～图6-81）

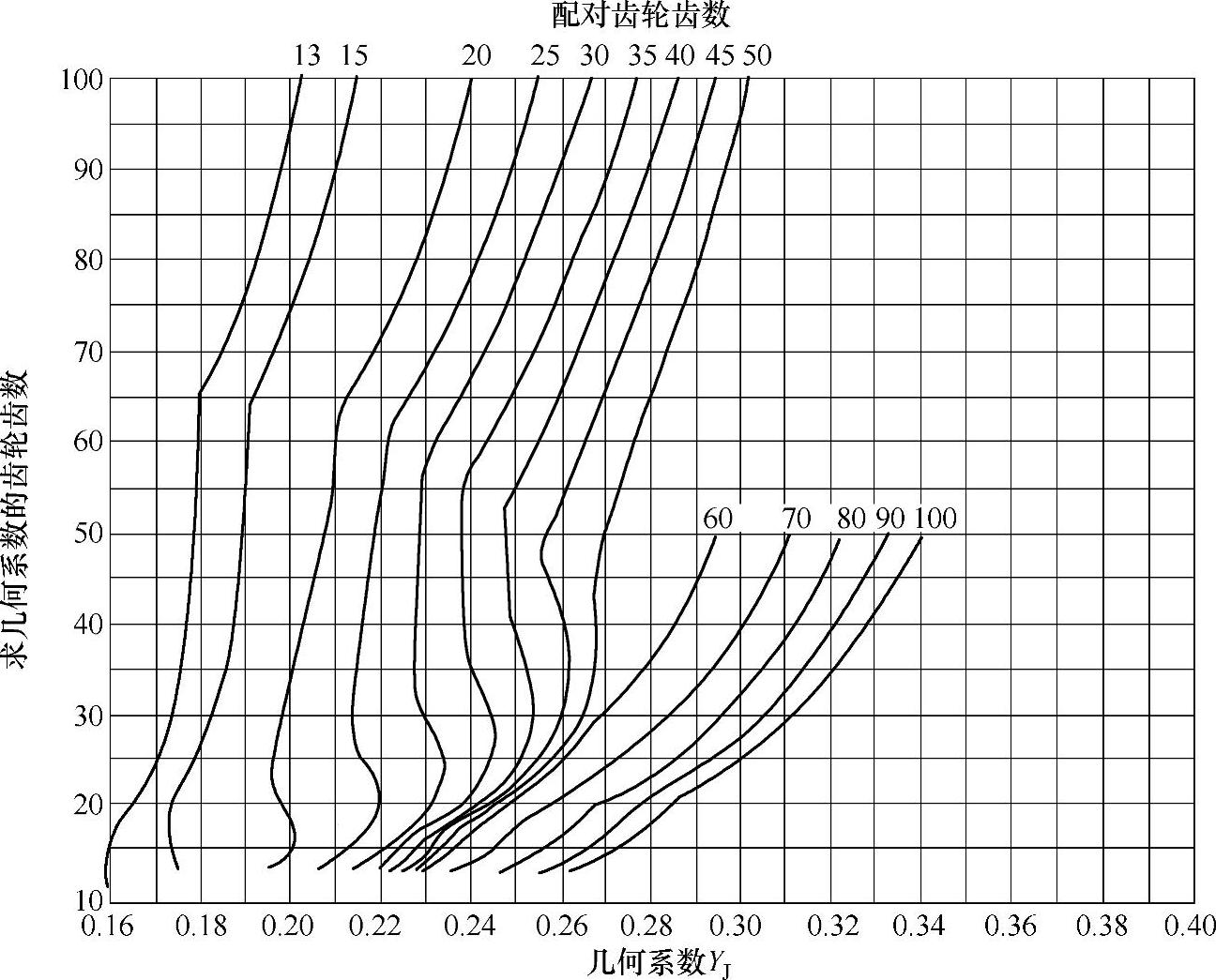
图6-70 Σ=90°、α_n=20°、刀刃半径为0.12m_et的直齿锥齿轮的几何系数YJ

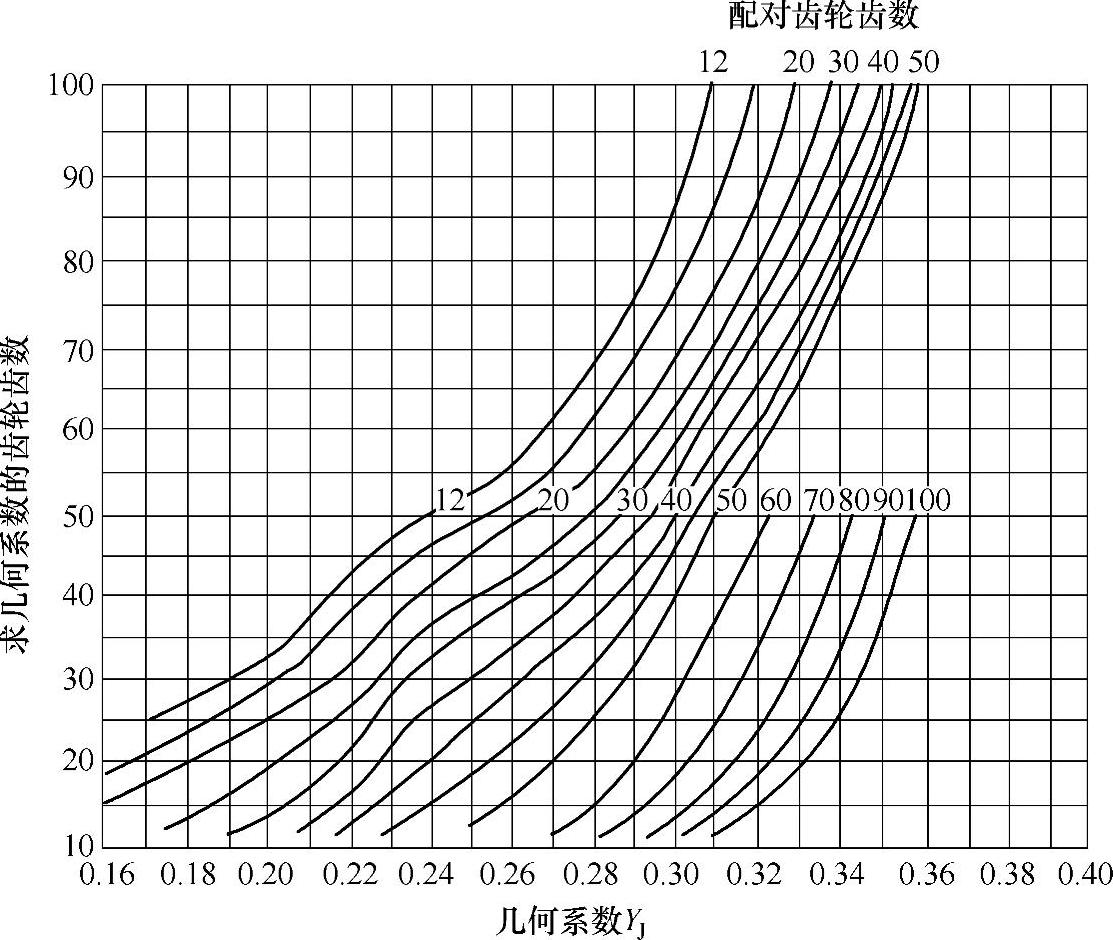
图6-71 Σ=90°、α_n=20°、β_m=35°、刀刃半径为0.12m_et的弧齿锥齿轮的几何系数Y_J

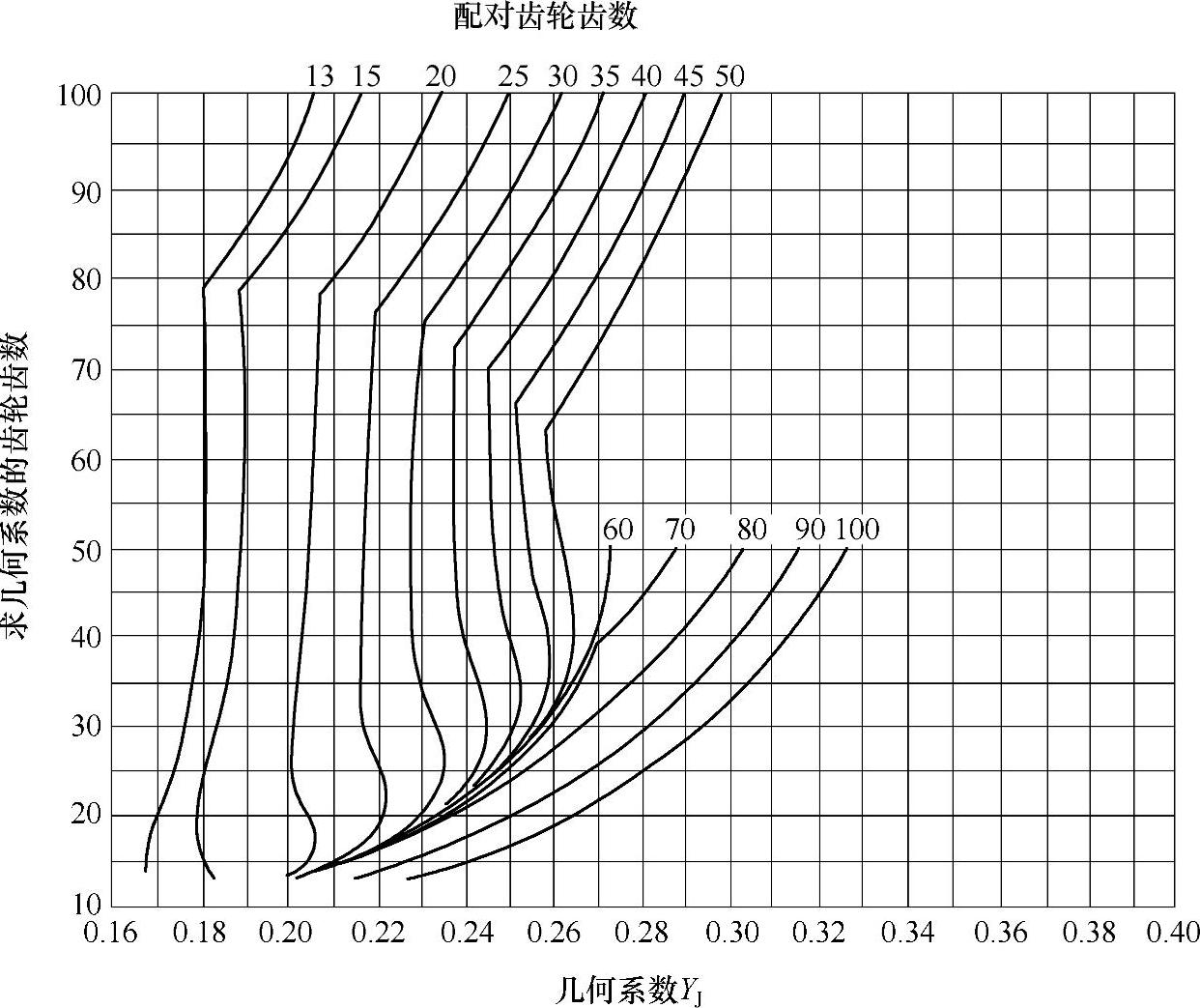
图6-72 Σ=90°、α_n=20°、刀刃半径为0.12m_et的大模数零度齿锥齿轮的几何系数Y_J

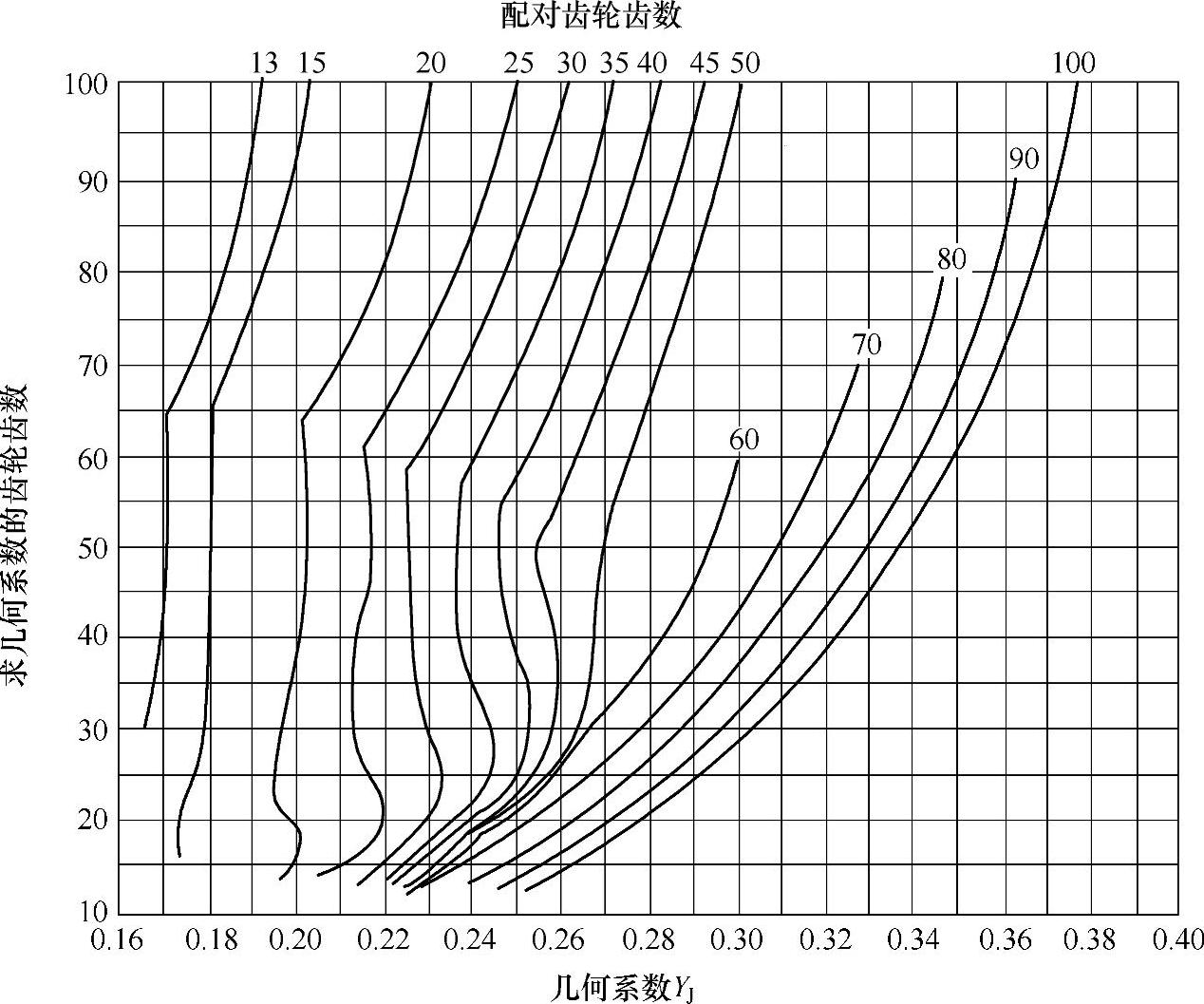
图6-73 Σ=90°、α_n=20°的鼓形直齿锥齿轮的几何系数Y_J

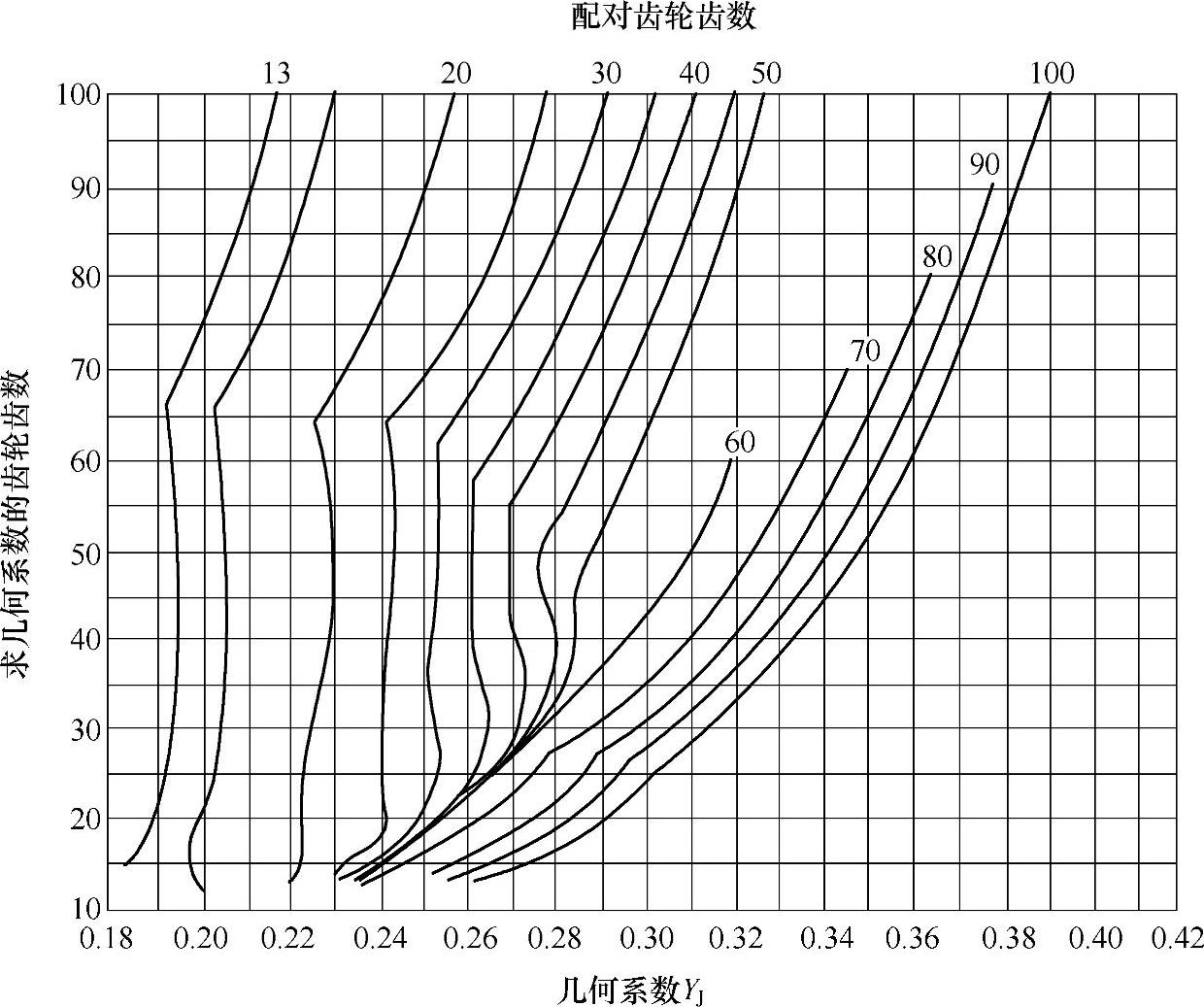
图6-74 Σ=90°、α_n=25°的鼓形直齿锥齿轮的几何系数Y_J

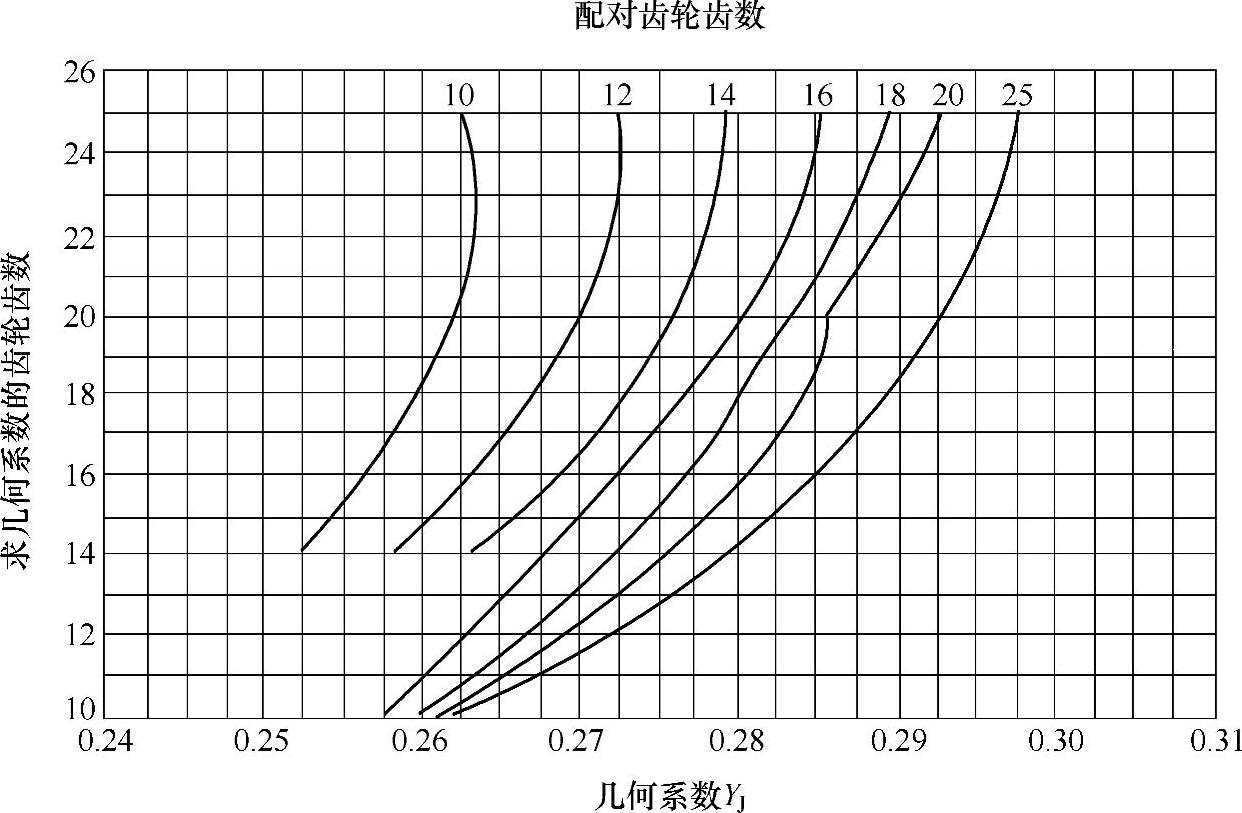
图6-75 Σ=90°、α_n=22.5°的鼓形直齿锥齿轮的几何系数Y_J

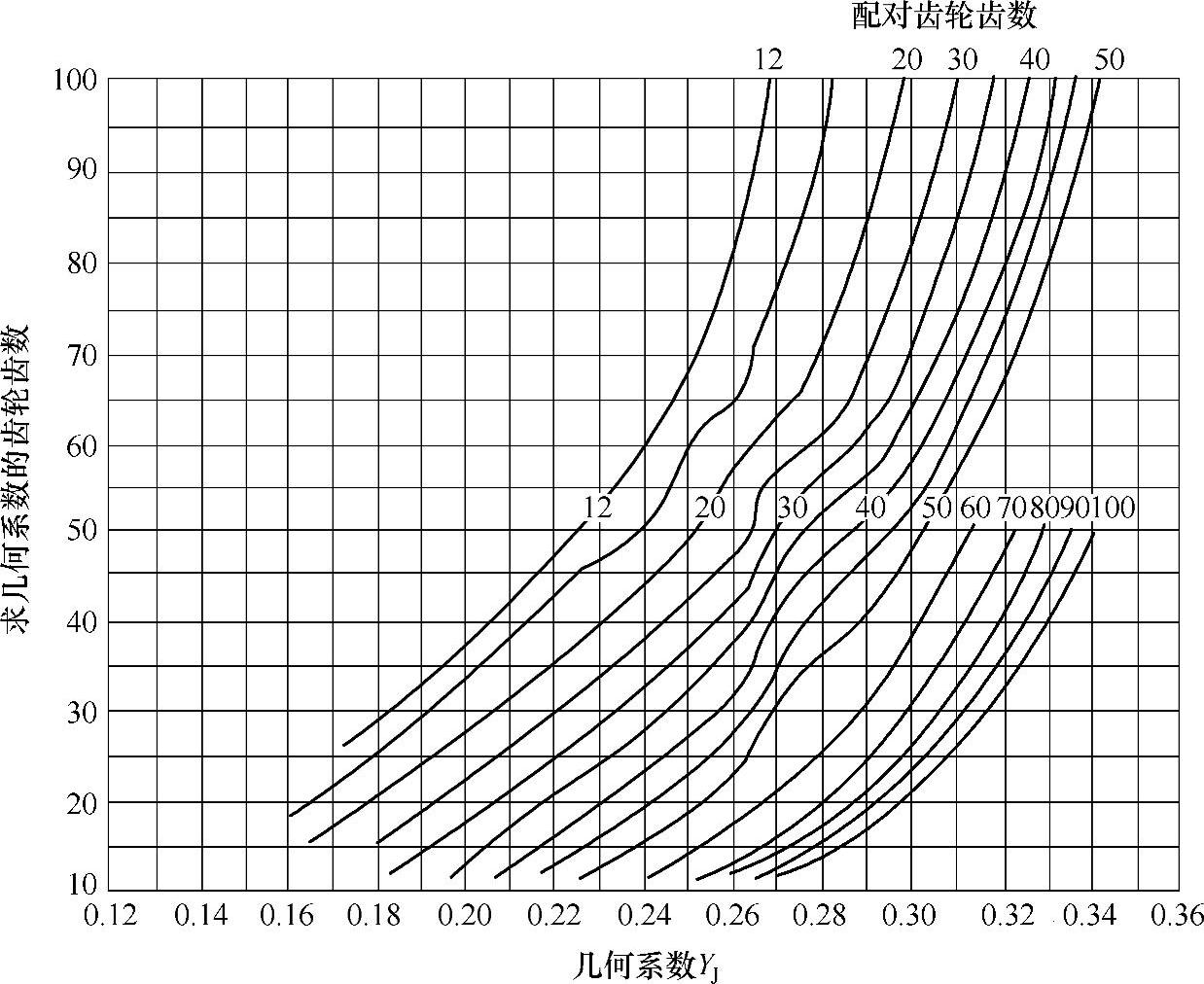
图6-76 Σ=90°、α_n=20°、β_m=35°的弧齿锥齿轮的几何系数Y_J

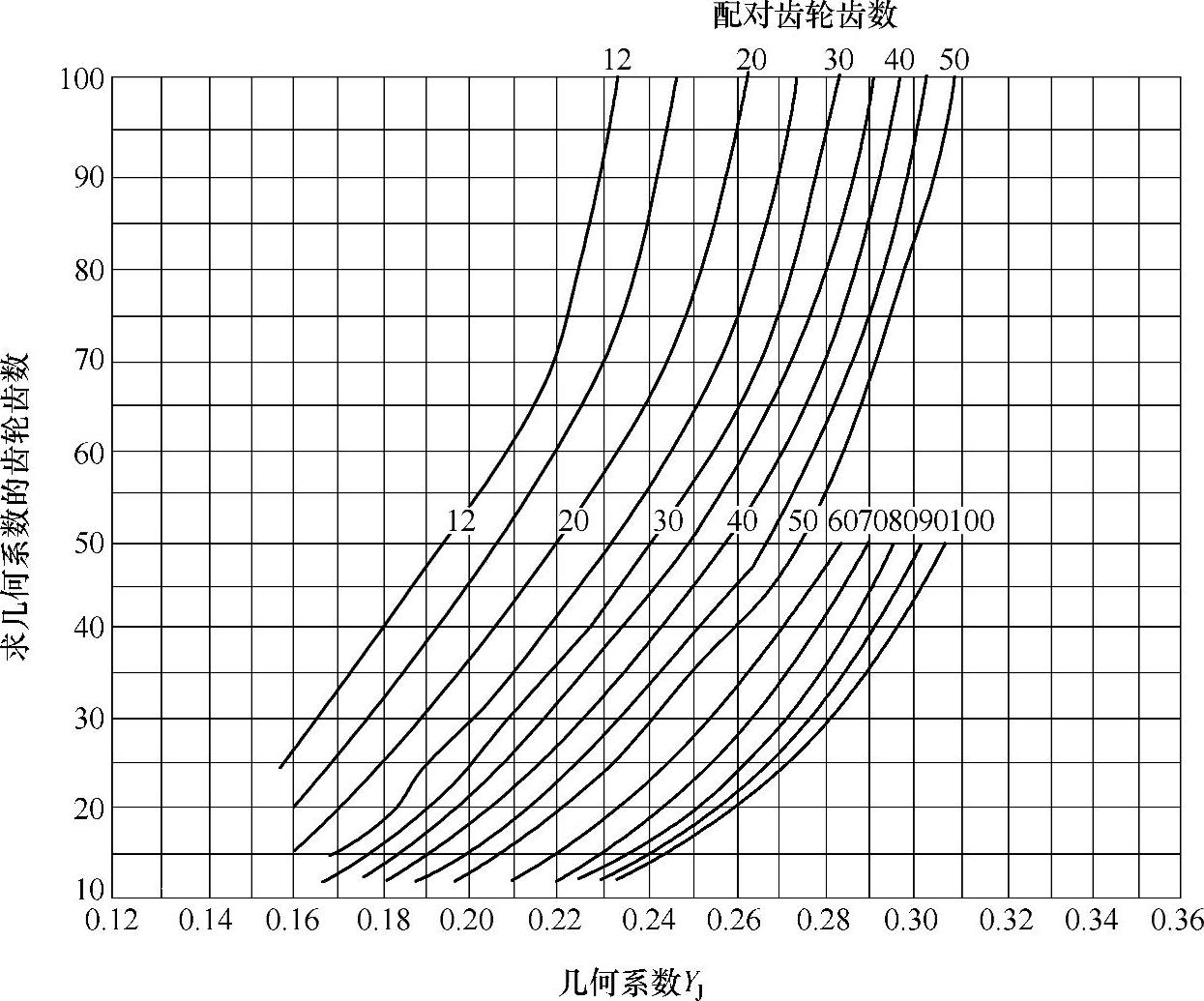
图6-77 Σ=90°、α_n=20°、β_m=15°的弧齿锥齿轮的几何系数Y_J

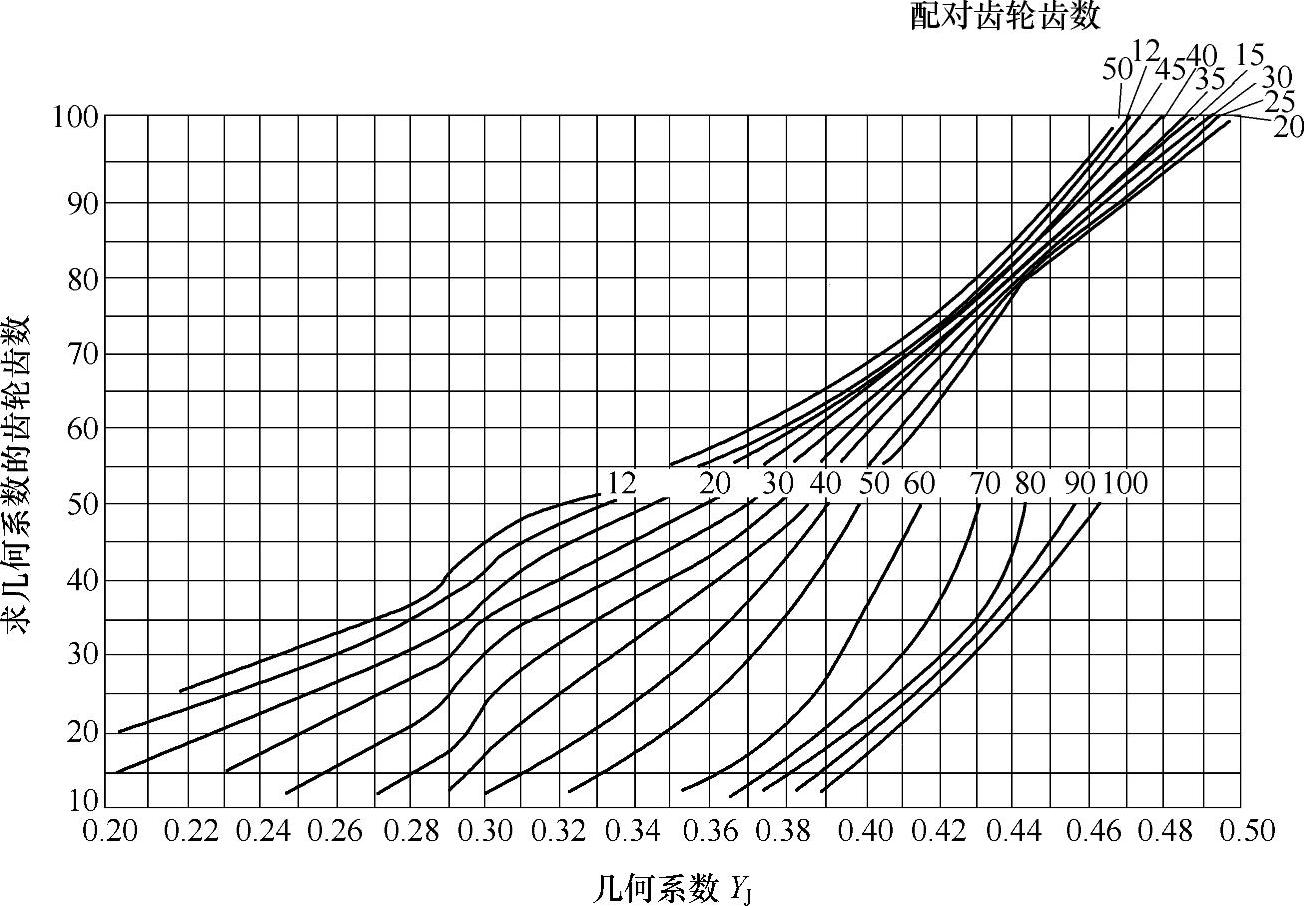
图6-78 Σ=90°、α_n=25°、β_m=35°的弧齿锥齿轮的几何系数Y_J

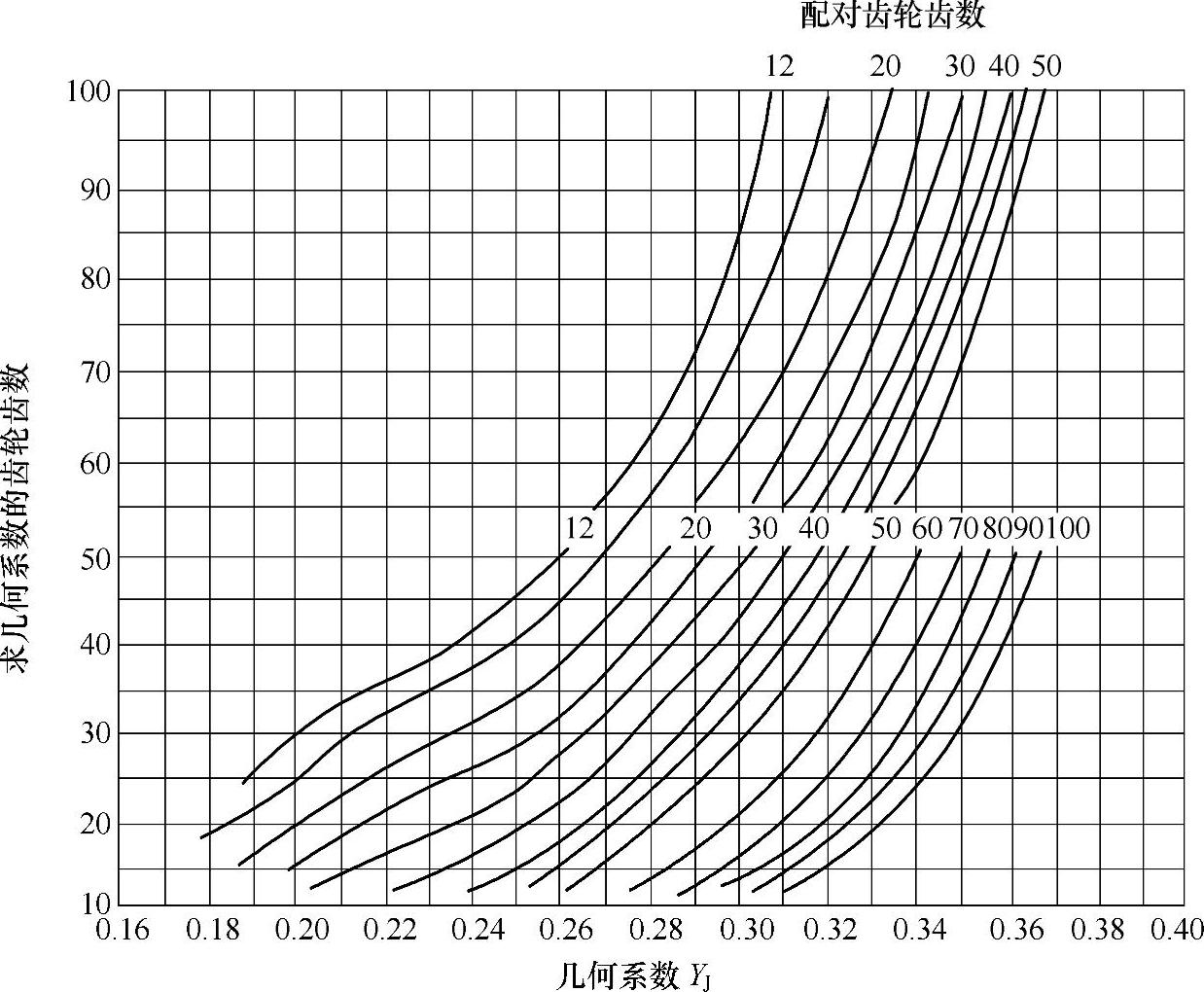
图6-79 Σ=60°、α_n=20°、β_m=35°的弧齿锥齿轮的几何系数Y_J

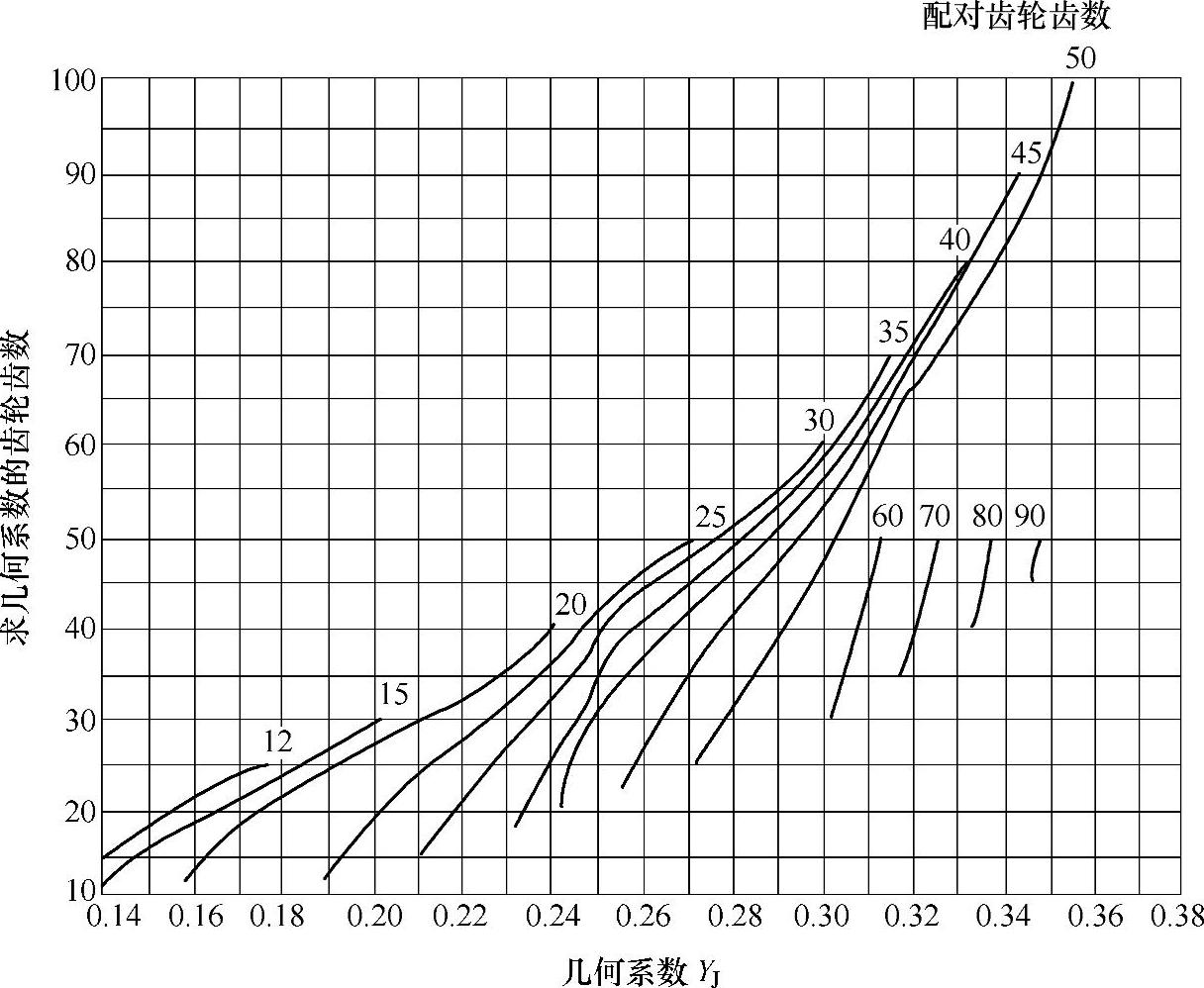
图6-80 Σ=120°、α_n=20°、β_m=35°的弧齿锥齿轮的几何系数Y_J

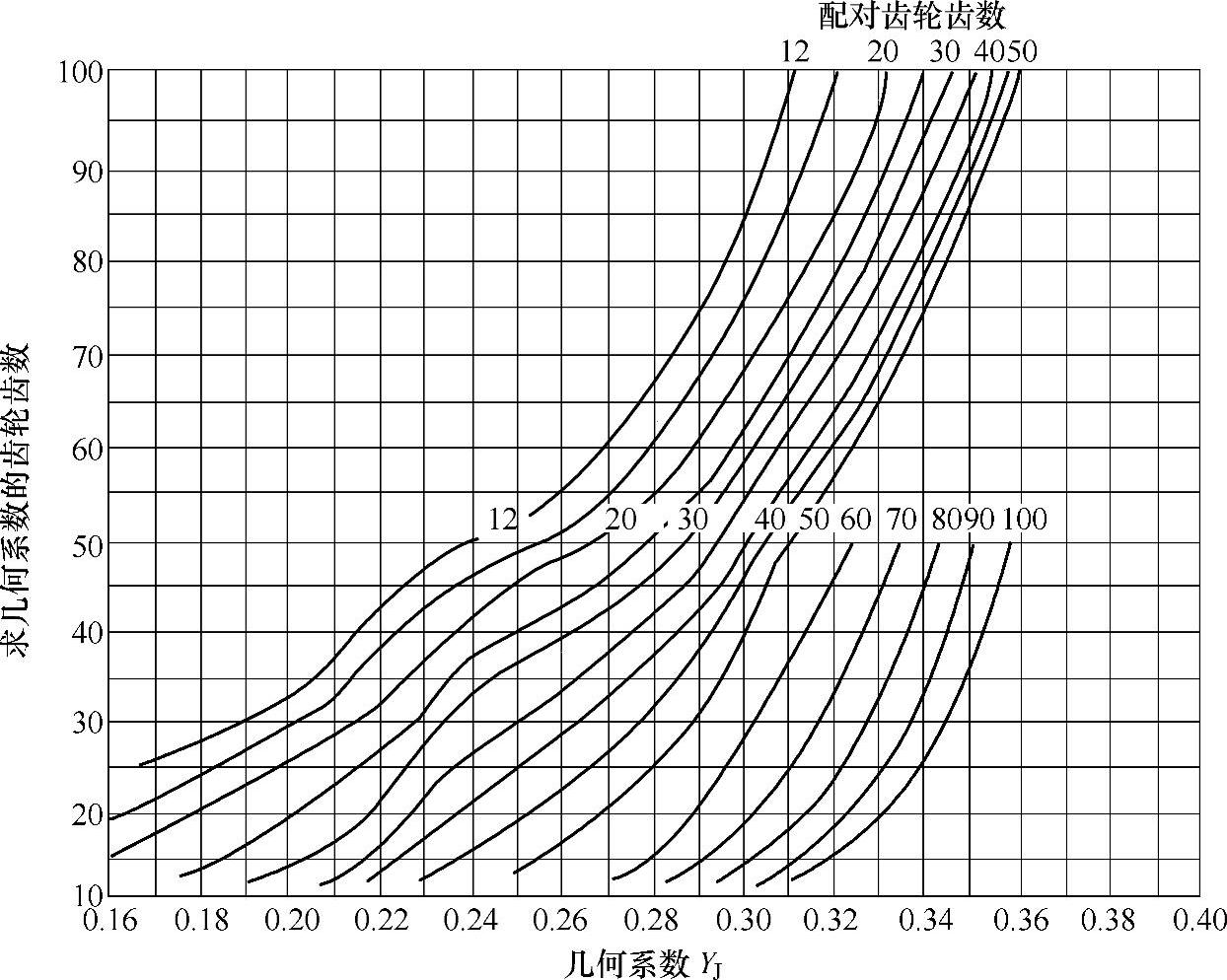
图6-81 Σ=90°、α_n=20°、β_m=35°的弧齿锥齿轮的几何系数Y_J