（1）范围

GB/T 10062中的计算公式为直齿、斜齿、零度齿和弧齿锥齿轮（除准双曲面齿轮外）的接触和弯曲强度的计算提供了一个统一的适用方法。适用于等高齿、收缩齿。

计算公式考虑了已知的影响轮齿点蚀与在齿根圆角处断裂的各主要系数。计算公式不适用于轮齿的下述损坏形式：塑性变形、微点蚀、表层压碎、焊合、磨损等。弯曲强度的计算公式适用于齿根圆角的断裂强度计算，但不适用于轮齿工作表面的弯曲强度计算，也不适用于轮缘或辐板、轮毂失效的强度计算。对于特种类型的锥齿轮的抗点蚀与弯曲强度承载能力可用恰当选择通用计算式中的各系数的数值来进行计算。GB/T10062不适用于接触不良的锥齿轮。

GB/T 10062适用于当量圆柱齿轮端面重合度ε_vα＜2的锥齿轮。对于大小齿轮的齿高变位系数总和为零（即啮合齿轮副的法向工作压力角等于基本齿条的法向压力角）的齿轮，该标准中给出的各种关系式是有效的。

注：准双曲面齿轮的承载能力的计算方法由切齿机床的制造厂家提供。

注意：当这个方法用于大的螺旋角、大的压力角和大的齿宽b＞10m_mn（m_mn为中点法面模数）时，GB/T 10062的计算结果应经过验证确定。

（2）应用

1）方法

①通则。GB/T 10062主要用于计算从图样或测量（重新计算）中获得必要数据的锥齿轮。在初步设计阶段，所获得的数据是有限的，对于某些系数可采用近似或经验的数值。此外，在某些应用场合或粗略计算中，某些系数可设定为“1”或某个常数。但此时应选用保守的安全系数[见（2）2）]。无论何种情况，如果A、B、C法的结果不一致，则优先选择实际尺寸、全负荷试验。如果A法的精确度与可靠度已被证明，与B法比较优先选用A法，同样B法与C法比较则优先选用B法。

②实际尺寸、全负荷试验。齿轮传动设计实际尺寸、全负荷的试验是预测整个齿轮系统性能（齿轮承载能力）的最有效的方法。试验方法不需要用A、B、C法中任一种计算来校验。然而，对于锥齿轮，习惯上用B法或C法进行初始设计，然后用试验方法来改进，以达到最佳的轮齿接触、工作的平衡性以及可调节性。

③A法。从其他类似的齿轮传动结构的运行中获得丰富的经验，从试验结果或现场数据的推论中获得满意的指导资料。包括在上述推论中的系数要用精确测试和传动系统的深入的数学分析或运行现场的经验等来评价。为使用A法，要知道齿轮载荷的全部数据，这些数据要清楚被描述并提供全部数学分析与试验的前提条件、边界条件、影响到结果的各种特征等。例如，这种方法的精确度要通过公认的齿轮测试来证实。对于这种方法，用户和供应者协商一致。

④B法。从其他类似的齿轮传动结构的运行中获得丰富的经验，从试验结果与现场数据的推论中获得满意的指导资料。推荐本计算方法用于设计方案的比较。此外，对某些系数给出了近似的方法及其评价的相关假定。对于给定工作条件下的相关假定的有效性要予以检验。

⑤C法。在评价某些系数时，如不能获得适当的试验结果或类似设计的现场经验，则要采用进一步简化的计算方法。上述简化计算方法对于特定的使用条件或某些特定的前提（例如，与验收试验相关的前提条件）是适用的。

2）安全系数。当选择安全系数时，允许的齿轮失效概率应小心地权衡，以平衡可靠度与成本之间的关系。如果在实际载荷条件下用试验齿轮箱的方法能精确鉴别齿轮的性能，则可采用较低的安全系数。安全系数由计算强度除以工作应力来确定。

除上述总的要求以及与表面接触疲劳强度（点蚀）和齿根弯曲强度（GB/T10062.2—2003、GB/T 10062.3—2003）有关的特殊的要求以外，只有当仔细考虑了材料数据的可靠度、计算所用载荷值的可靠度后才能确定安全系数。在给定的失效概率条件下，用于计算的材料的疲劳极限才是有效的（GB/T 3480.5—2008材料的疲劳极限在失效概率为1%的情况下有效）。当安全系数增加时，则失效的危险降低，反之亦然。如果载荷或系统对振动的响应是估算的而不是测试所得的，则应采用较大的安全系数。

在确定安全系数时，要考虑下述的变化：

——由于制造公差引起的齿轮几何参数变化：

——对中度的变化；

——由于化学成分、纯净度与微观结构的变化（材料质量与热处理）引起的材料变化；

——润滑与齿轮使用寿命期间维护的变化。

安全系数取值的合理性取决于计算中的假定的可靠性（例如：计算的载荷假定）以及齿轮本身所要求的可靠性（可能发生的齿轮失效）。

齿轮产品应具有接触强度的最小安全系数S_Hmin=1，弯曲强度的最小安全系数S_Fmin=1.3（对弧齿锥齿轮），S_Fmin=1.5（对于直锥齿轮或β_m≤5°的斜齿锥齿轮）。

对于点蚀损坏与断齿的最小安全系数，供应者与用户应协商一致。

3）强度系数

①试验。对齿轮箱的性能的考验，最有效的方法是实际尺寸、全负荷的试验。然而，这个方法受到高成本的限制。当类似的设计有丰富的经验并能获得有关数据时，那么可从上述经验与数据中通过推断分析获得满意结果。另一方面，当不能获得适用的测试数据与现场运行数据时，应保守地选取强度系数值。

②制造公差。强度核算各系数的取值应基于零部件加工的最低的规定精度。精度等级应按GB/T 10095.1—2008齿距偏差确定。

③隐含的精度。当系数的经验数据由曲线给出时，GB/T 10062提供了曲线拟合方程，以便编程。

注：拟合曲线的常数和系数明显地比经验数据高一些。

4）其他因素

①综述。除影响接触强度和弯曲强度的各系数外，其他相关系统因素对整个传动性能也有重要影响。上述的影响在计算时必须考虑。

②润滑。只有当运转的齿轮轮齿配有与载荷、速度和齿面粗糙度相适应的润滑油（有合适的粘度和添加剂），并有足够润滑油供给齿轮与轴承，而且保持合适的运行温度时，GB/T 10062计算公式所确定的承载能力才有效。

③不对中误差。许多齿轮传动系统需外部支承基础（例如机器的底座）以保证齿轮啮合的正确性。如果这些支承基础设计不良、存在初始的不对中误差，或由于弹性变形或热变形或其他影响因素，使这些支承基础在运行中变成不对中的状态，对整个齿轮传动系统的性能将产生不利的影响。

④变形。由于悬臂、径向和轴向载荷造成的齿轮的支承箱体、轴与轴承的变形影响到轮齿啮合过程的接触。因变形是随载荷而变化的，要在不同载荷下都获得好的轮齿接触是很难的。一般来说，原动机与工作机械的外载荷所引起的变形会降低齿轮的承载能力。外力与内力引起的变形在确定轮齿实际接触时都应充分考虑。

⑤材料和冶金质量。大多数锥齿轮由表面渗碳淬火钢制造。这种材料和其他材料的疲劳极限应在锥齿轮试验基础之上来确定。材料疲劳极限（基于钢的冶金制造与热处理的不同状态来确定）从GB/T 3480.5—2008中查取。为选取材料的疲劳极限，应规范材料的硬度、拉伸强度以及质量等级。

注：高质量等级的钢具有高的疲劳极限，低质量等级的钢具有低的疲劳极限.

⑥残余应力。任何一种含铁的材料具有一种表层-心部硬度梯度，这表明存在残余应力。如果处理恰当，齿面表层将是压应力，因此提高了轮齿弯曲疲劳强度。喷丸、表面渗碳、感应硬化（如果处理得当）是造成轮齿表面压应力的通用方法。热处理后的不恰当的磨齿工艺可能降低残余压应力导致轮齿齿根圆角处的残余拉应力，从而降低了材料的疲劳极限。

⑦系统动力学。所使用的分析方法公式中包括动载系数K_V，由于轮齿制造误差产生了附加载荷，从而降低了齿轮的承载能力。一般来说，本分析计算方法提供了简化值，以便于应用。

由于原动机与工作机械联结的质量的相对运动，并因此而引起的系统的动力响应产生了附加的轮齿载荷。使用系数K_A仅考虑原动机与工作机械的运行特征。但应认识到齿轮传动副、齿轮箱体的误差和工作机械等诸多因素在接近系统的固有频率处诱发激振，共振能产生比正常载荷大几倍的载荷。因此，涉及到临界使用情况时，推荐进行整个系统的分析。这种分析包括原动机、工作机、联轴器、安装条件、激振的根源等整个系统。必须计算自振频率、振型、动态响应的振幅等。

⑧接触斑点。为补偿轴和安装基础的变形，在制造过程中绝大多数锥齿轮的轮齿在齿高与齿长方向是鼓形的。这样造成了滚动检查时，在轻载荷下为局部接触斑点。除另有规定外，在设计载荷下轮齿接触斑点应分布整个齿面，不能有集中于大小齿轮边缘的斑点。对于未按鼓形齿加工的并且接触斑点不良的锥齿轮，使用强度计算公式时需要对GB/T 10062的系数修正。

⑨腐蚀。齿轮的腐蚀会明显降低轮齿的弯曲强度与接触强度。

5）基本计算公式中的影响系数 基本计算公式包括了由几何参数确定的系数或常规方法确定的系数，上述系数都要根据它们的计算式计算。

GB/T 10062的计算公式也包括了反映制造偏差和齿轮箱工作周期的系数。考虑到众多的影响，这些系数通称为影响系数。虽然这些系数按相互独立来处理，但在一定程度上是相互影响的（难作定量分析）。这些系数包括影响载荷的系数K_A、K_V、K_Hβ、K_Fβ、K_Hα、K_Fα和影响许用应力的诸系数。

还包括反映应力与寿命关系的系数。

各影响系数可用不同的方法来确定。如果需要，系数代号可加下标A、B、C等。除另有规定外（例如应用标准中有规定），对重要的传动优先选用更精确的方法。当计算影响系数的方法不能简明识别时，建议使用补充下标。

对于某些应用情况，必须采用不同的方法选择各系数（例如：确定动载系数、齿间载荷系数的不同的方法）。书写计算报告时，所采用的方法用扩展的下标注明，例如：K_V-C，K_Hα-β。

（3）外部作用力与使用系数K_A

1）名义切向力、名义转矩、名义功率GB/T 10062中，把小齿轮转矩用于基本的应力计算公式中。为确定轮齿的弯矩或齿面上的力，在分锥中点齿宽处计算切向力。

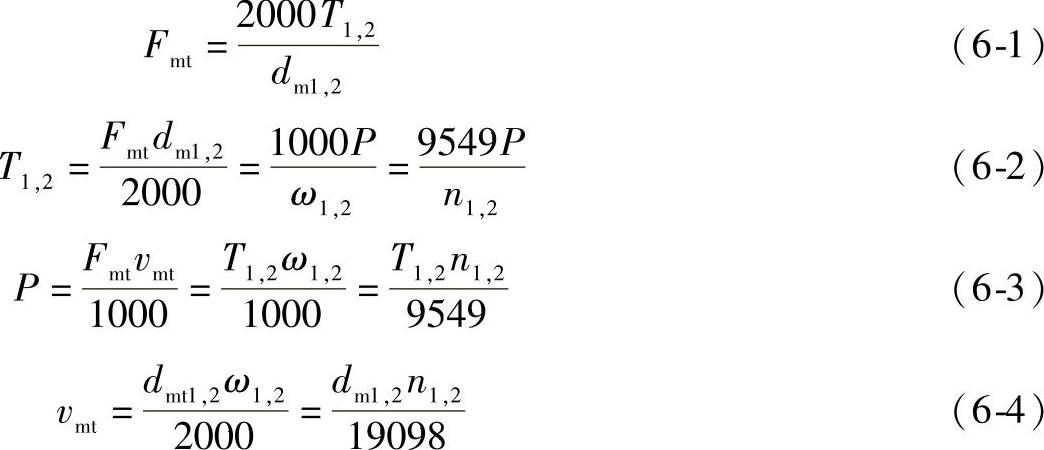
式中各参数的含义参见GB/T 10062.1—2003，下同。

工作机械的名义转矩是决定性的。该工作转矩是在最苛刻或常规的条件下长期运转时的转矩。

例如：最大的恒定的轧制转矩，最大的起重转矩。

如果原动机的名义转矩相当于工作机械的转矩，也可用原动机的转矩。

2）变载荷工况 如果载荷不是均匀的，则必须仔细分析，其中要考虑外部动载系数与内部动载系数。要确定齿轮预期寿命内的各种载荷及其运行时间。按基于Miner法则（见GB/T 3480—1997）的方法，根据转矩图谱确定齿轮的当量寿命。

3）使用系数K_A如果没有可靠的经验数据，或不能获得由实际测试或综合的系统分析确定的载荷谱时，可采用根据式（6-1）确定的名义切向力F_mt与使用系数K_A进行计算。该使用系数允许任何外部施加的动载荷超过名义工作转矩T₁。

①影响外部动载荷的系数。在确定使用系数时，应考虑到下述事实：许多原动机会产生瞬时尖峰转矩，该尖峰转矩比按额定功率和工作机械所确定的转矩要大许多。有许多可能的动态过载源，应予以考虑：

——系统振动；

——临界速度；

——加速转矩；

——超速；

——系统运行中的突然变化；

——制动刹车；

——反向转矩（如车辆的减速制动的转矩），它导致轮齿反向齿面受载。

在齿轮传动工作范围内进行临界速度的分析是必要的。如果临界速度存在，为了消除共振或对系统提供阻尼以尽量降低齿轮和轴的振动，应对整个齿轮传动系统的设计进行修改。

②使用系数的确定。对一个特定的应用场合的使用经验进行全面分析，是确定使用系数最好的方法。例如船用齿轮，它承受周期性的尖峰转矩（扭振），并且设为无限寿命，使用系数可定义为周期性尖峰转矩与名义额定转矩之比。名义额定转矩由额定功率与速度确定。

如果齿轮承受有限次数的并超过周期尖峰转矩的变载荷，其影响可直接按增大使用系数（表示载荷图谱的影响）的方法表示。

如果不能获得使用经验数据，则应进行全面的分析研究。如果确定使用系数的这两种方法都不能实现.则可用表6-31提供的近似值。

（4）动载系数K_V

1）概述 动载系数K_V是考虑轮齿制造质量对速度，载荷的影响以及下面所述各种因素的影响。动载系数表示轮齿总载荷（包括内部动态影响）与所传递切向载荷的比例关系，并用载荷总量（内部有效动载荷加所传递的切向载荷之和）除以传递的切向载荷表示。轮齿内部动载荷的因素分为两种种类：设计与制造。

2）设计 设计因素包括：

——节线速度；

——轮齿载荷；

——旋转元件的惯量与刚度；

——轮齿刚度变化量；

——润滑剂的性能；

——轴承刚度与箱体结构；

——临界速度和齿轮箱的内部振动。

3）制造 制造因素包括：

——齿距偏差；

——节圆面对旋转轴心的径跳；

——齿面偏差；

——啮合轮齿副的相配性；

——元件的平衡；

——轴承的配合与预载荷。

4）传动误差 即使输入的转矩与速度恒定，也存在齿轮质量的明显振动及其产生的轮齿动载荷。这些动载荷由啮合轮齿的相对运动产生，振动是由传动误差导致的激振引起的。一对齿轮副理想的运动要求输入与输出之间速比恒定。传动误差定义为对啮合齿轮副均匀角运动的偏差。传动误差受许多偏差的影响，这些偏差是：理想齿轮与设计齿轮的齿形偏差、制造加工方法的偏差以及运行条件等。运行条件包括下列各项：

①节线速度。激振的频率取决于节线速度与模数。

②轮齿一个啮合周期的齿轮啮合刚度的变化。这是一种激振源，对直锥齿轮与零度锥齿轮而言特别明显。重合度大于2.0的弧齿锥齿轮的刚度变化较小。

③齿轮传递的载荷。由于变形取决于载荷，设计的轮齿齿廓修形只能保证一种载荷下均匀的速比。载荷与设计载荷不同时传动误差将增加。

④齿轮和轴的动态不平衡。

⑤使用环境。轮齿齿廓的过多磨损与塑性变形将使传动误差增大。齿轮传动应有合适的润滑系统、封闭的运行空间、密封条件以维持一个安全的运行温度和无污染的环境。

⑥轴的对中度。齿轮载荷和齿轮、轴、轴承、箱体的热变形影响到轮齿啮合的对中度。

⑦轮齿摩擦引发的激振。

5）动态响应 轮齿的动载荷受下述因素影响：

——齿轮、轴和其他主要内部零件的质量；

——轮齿、轮体、轴承与箱体的刚度；

——阻尼、阻尼源主要是轴承与密封，其他的阻尼源包括齿轮轴的滞阻、滑动面与联轴器的粘性阻尼。

6）共振 当一种激振频率（轮齿啮合频率、轮齿啮合倍频）等于或接近齿轮传动系统的固有频率时，共振会引起高的轮齿动载荷。当某一转速产生共振引起内部动载荷变大时，应避免在这种转速范围下运行。

①轮体共振。高速与轻载的齿轮的轮体可能具有在工作速度范围内的固有振动频率。如果轮体受到接近其固有频率激振时，则共振产生的变形要引起轮齿高的动载荷。薄板形或薄筒形振动能引起轮体的破坏。

当轮体共振时，确定动载系数K_V的B法和C法不再适用。

②系统共振。原动机、齿轮箱、工作机械、联结轴与联轴器组成一个系统，齿轮箱是该系统中的组成部分。该系统的动态响应取决于系统的组成。在一定的情况下，系统的某一固有频率可能接近与工作转速相关的激振频率。在这样的共振条件下，齿轮箱的运行必须进行仔细分析评价。对于临界状态的齿轮传动，推荐对整个系统进行详尽的分析。当确定使用系数时，同样也要详尽分析。

7）计算方法 一对锥齿轮传动是一种非常复杂的振动系统。不能仅考虑一对锥齿轮来确定动态系统与固有振动频率（引起动载荷）。小齿轮轴的对中度可调整改变，主要取决于装配调整操作人员的水平、间隙、齿轮轴、轴承、箱体等的弹性变形。对中度的轻微的调整变化将改变锥齿轮副的相对旋转角度，也改变轮齿上的动载荷。齿长和齿廓的鼓形妨碍了真正的共轭啮合并使轮齿精度难于确定。

在上述情况下，动载系数的可靠数值可由测试方法充分验证过的数字模型来确定。如果已知的动载荷已加到名义的传递载荷上，则动载系数取1。

确定K_V的方法有A法（K_V-A）、B法（K_V-B）和C法（K_V-C）。

①A法（K_V-A）。K_V-A由综合的分析法来确定，由类似的设计经验所证实，并在确定过程中采用下述步骤：

a）建立包括齿轮箱在内的整个动力传动振动系统的数学模型。

b）测试或用可靠的模拟程序计算受载下的锥齿轮副的传动误差。

c）用系统模型a）和传动误差b）引起的激励来分析小齿轮轴和大齿轮的动态响应。

②B法（K_V-B）。该法作了简化，假定：包括大齿轮与小齿轮为综合质量在内的一对锥齿轮副构成一种基本单质量弹簧振动系统，弹簧刚度是接触轮齿的啮合刚度。根据上述假定，K_V-B法中没有包括由于轴及其联结的质量的扭振而产生的力。如果除锥齿轮副外的其他质量是由相对低的扭转刚度的轴联结时，这是符合实际的。对于带有很大横向柔性的轴的锥齿轮副，真实的固有频率低于计算的频率。

动载荷的大小取决于齿轮的精度，即齿廓形状和齿距精度。对锥齿轮而言，确定齿廓形状偏差是困难的（不是渐开线型）。另一方面，齿距偏差能相对容易地测出。因此，该方法在确定动载系数时，用齿距偏差代表传动误差的数值。

在计算K_V-B时，需要下述数据：

a）齿轮副的精度（齿距偏差）。

b）小齿轮与大齿轮的质量惯性矩（尺寸与材料密度）。

c）轮齿的刚度。

d）切向载荷。

a.速度范围。无量纲的基准速度N

式中，n_E1是按式（6-6）确定的共振转速。

借助于基准速度N，全部速度范围可分为4个区段：亚临界区、主共振区、超临界区与过渡区（主共振区与超临界区之间）。

由于某些零件（如轴、轴承、箱体）的刚度没有包括阻尼的影响，所以共振速度要高于或低于按式（6-6）算得的速度。为安全起见，共振区定义为0.75<N≤1.25。

用K_V-B法计算的各区段如下：

——亚临界区，N≤0.75，用A法或B法确定；

——主共振区，0.75<N≤1.25（在此区段的运行必须避免，若不可避免则必须用A法分析）；

——过渡区，1.25<N<1.5，用A法或B法确定；

——超临界区，N≥1.5，用A法或B法确定。

关于速度范围的更详细的资料见GB/T 3480—1997。

b.共振速度

对于圆柱直齿轮，用c_γ0=20N/（mm·μm）。对圆柱斜齿轮的研究表明，螺旋角增加时，刚度降低。另一方面，锥齿轮的轮齿在锥体上的螺旋形布置加强了斜齿、弧齿锥齿轮的刚度。由于缺乏更深入的了解，在平均的条件下（F_mtK_A/b_e≥100N/mm，与b_e/b≥0.85），圆柱直齿轮的刚度对锥齿轮是适用的。因此，c_γ能按下式确定：

c_γ=c_γ0C_FC_b（6-8）

式中 c_γ0——平均条件下的轮齿啮合刚度，可采用20N/（mm·μm）值；若经验表明有另外的数值对锥齿更适用，则要用该数值替换20N/（mm·_μm）；

C_F、C_b——对非平均条件下的修正系数；

对于F_mtK_A/b_e≥100N/mm C_F=1（6-9）

对于F_mtK_A/b_e＜100N/mm C_F=（F_mtK_A/b_e）/（100N/mm） （6-10）

对于b_e/b≥0.85 C_b=1 （6-11）

对于b_e/b<0.85 C_b=b_e/（0.85b） （6-12）

b_e为有效齿宽。有效齿宽b_e是接触斑点的实际长度。在满载条件下，接触斑点的长度是齿宽的85%。如果在受载条件下不能获得接触斑点长度的数据，则采用b_e=0.85b。

图6-38 用于确定动载系数的近似动态等效圆柱齿轮

如果精确确定锥齿轮副的惯性质量矩m₁*和m₂*，由于制造成本或其他原因不能实现时（在设计阶段），则常用轮体设计的锥齿轮可用近似等效的圆柱齿轮代替（下标x）（见图6-38）。

例如，对α_n=20°的钢制齿轮（ρ=7.86×10^-6kg/mm³）为

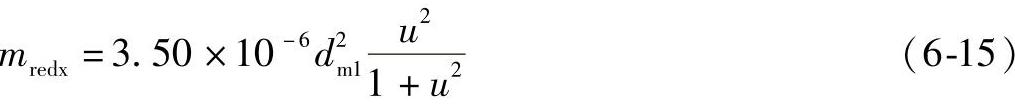
用c_γ=20N/（mm·μm）代入式（6-5）与式（6-6）：

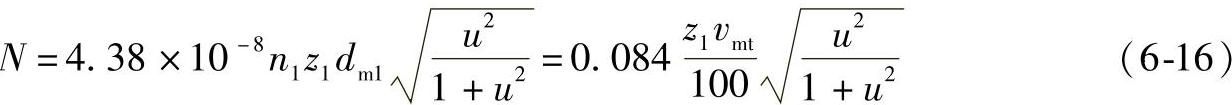
用图线确定实心钢制小齿轮和实心钢制大齿轮相啮合的共振速度，见图6-39。

c.亚临界区（N≤0.75）。车辆齿轮与工业齿轮的常用运行范围。

K_V-B=NK+1 （6-17）

按前面给出的B法的假定，采用下式：

c_γ=20N/（mm·μm））

式中：

f_peff=f_pt^-yp，yp≈ya

y_a见（6）5），f_pt见（6）3）①，c_v1，2与c_v3见表6-25。

注：齿顶修缘的影响没有考虑。因此，对于具有齿廓修形的锥齿轮副，上述计算偏于安全。

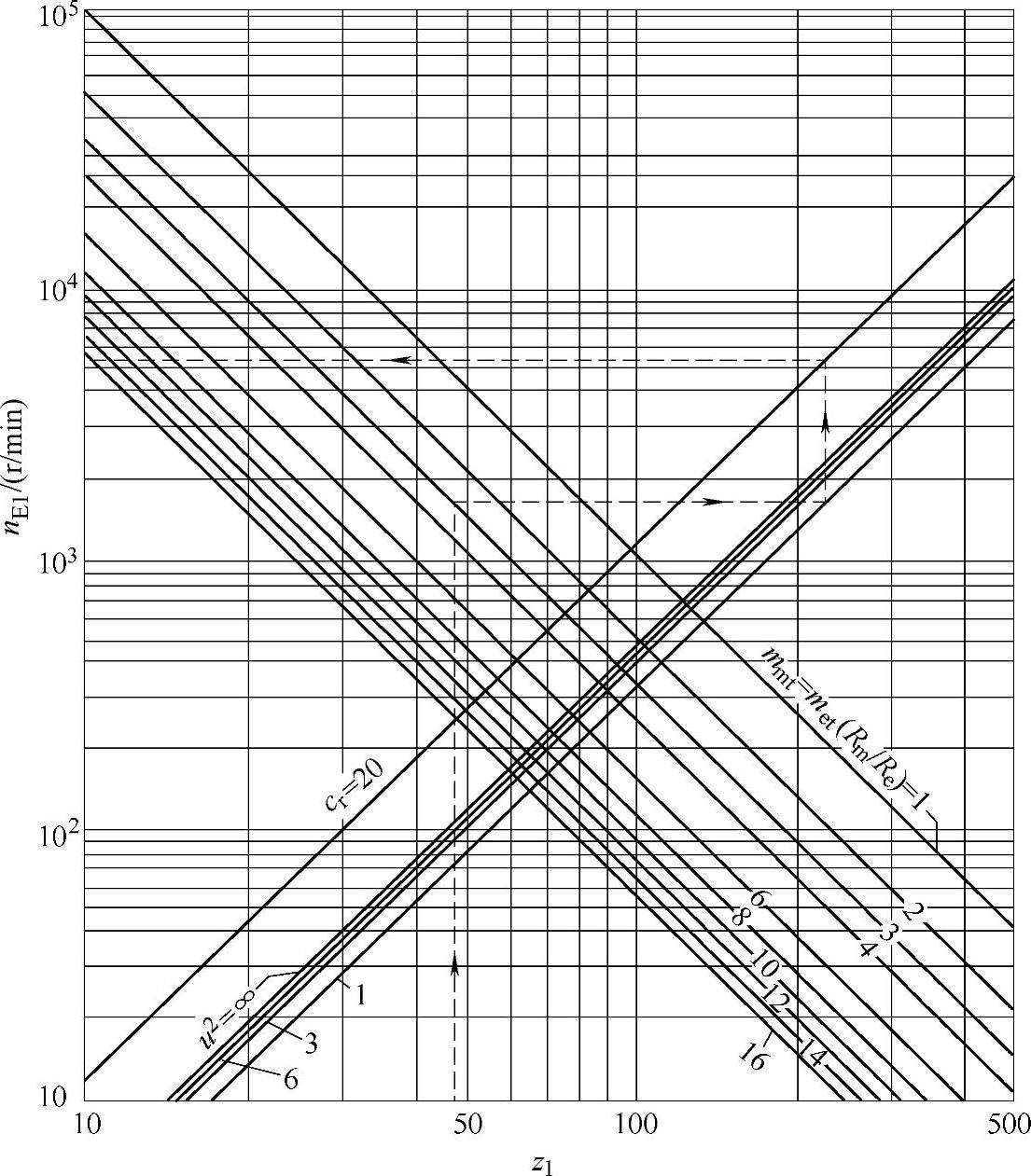
图6-39 确定共振速度n_E1的图线（用于实心钢制小轮和实心大轮的啮合，

对圆柱齿轮，采用c₀′=14N/（mm·μm）。对圆柱斜齿轮的研究表明，螺旋角增加时，齿的刚度降低。另一方面，锥齿轮的轮齿在锥体上的螺旋形布置加强了斜齿、弧齿锥齿轮的刚度。由于缺乏更深入的了解，在平均的条件下（F_mtK_A/b_e≥100N/mm，与b_e/b≥0.85），圆柱直齿轮的刚度对锥齿轮是适用的。因此，c′可按下式确定：

c′=c₀′C_FC_b （6-19）

式中 c₀′——平均条件下的单齿刚度；

C_F、C_b——非平均条件下的修正系数，见式（6-9）～式（6-12）。

d.主共振区（0.75<N≤1.25）。按B法的假设，用下式计算：

c_v1，2与c_v4见表6-25。

e.超共振区（N≥1.5）。高速齿轮与类似要求的齿轮在此区域中运行：

c_v5，6与c_v7见表6-25。

表6-25 式（6-18）～式（6-21）中的影响系数c_v1～cv7

①用于ε_vγ，见式（6-81）。

②齿距偏差的影响系数，假定为常数。

③齿廓偏差的影响系数。

④啮合刚度周期变化量的影响系数。

⑤考虑由啮合刚度的周期变化量所激励的扭振的影响系数。

⑥在超临界区，c_v5与c_v6影响系数对K_V-B的影响对应亚临界区c_v1与c_v2的影响。

⑦本影响系数考虑由于啮合刚度的变化量而产生的作用力的一个分量（这个作用力的分量是在基本恒速下由轮齿弯曲变形引起的）。

f.中间区（1.25<N<1.5）。在本区域中，动载系数在N=1.25的K_V-B与N=1.5的K_V-B之间用线性插值法确定。K_V-B按式（6-20）与式（6-21）计算。

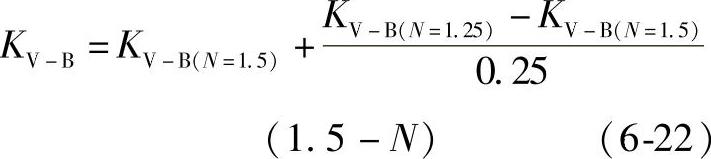
④C法（K_V-C）

a.综合评述。图6-40为动载系数图线，当缺乏专业的动载荷知识时可采用这些图线。图6-40的图线以及下面给出的计算公式是建立在经验数据基础之上的，未考虑共振（见（4）、6））。

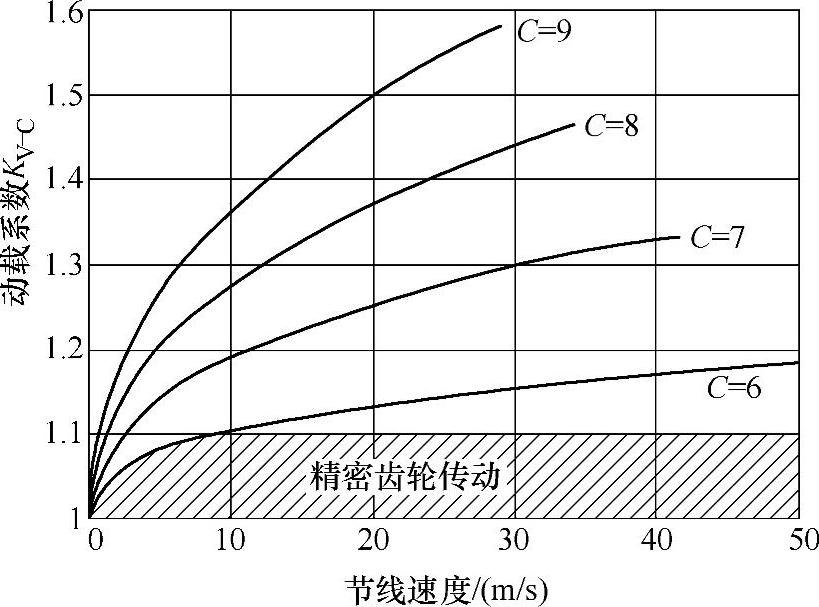
图6-40 动载系数KV-C

由于经验图线的近似特性和在设计阶段缺乏齿轮制造误差实测值，动载系数曲线必须在制造方法的经验以及考虑影响到设计的运行条件的基础之上来选择（见（4）.4）.①）。在大多数情况下，根据以前齿面的接触斑点的经验是有帮助的。

由曲线6～9与精密齿轮传动（（4）.4）.④.b））选择K_V-C是基于传动误差（见（3）、4））基础之上的。如果不能获得传动误差，则评价齿面上的接触斑点也是合理的。如果每侧齿面的接触斑点不一致，则齿距精度（齿距偏差）作为精度的代表数值，以确定动载系数。C是精度等级系数，按GB/T 10095.1给出的计算式计算。

b.精密齿轮传动。当齿轮传动采用很高精度等级工艺控制方法来制造时（一般情况下，当GB/T 10095.1—2008的C≤5时，或设计制造与使用经验保证为低传动误差时），K_V的值可取1.0与1.1（取决于类似应用的经验和实际达到的精度）。为了正确使用K_V的上述数值，齿轮传动必须保持精确的对中度和充分的润滑，使得在运行条件下保持该齿轮传动的全部精度。

c.经验曲线。图6-40中表示的C=6至C=9的经验曲线是由下述各式得出的：

6≤C≤9

6≤z≤1200或10000/m_mn（取较小的值）

1.25≤m_mn≤50

在经验与深入考虑动载的影响因素的基础上，曲线可延长超过图中的端点处。为计算机的计算，式（6-23）定义为图形中曲线端点的计算公式。

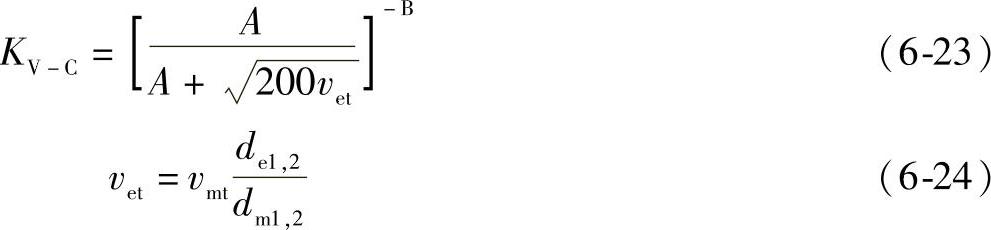
式中

C为按GB/T 10095.1—2008确定的精度等级系数（用m_mn与d_m确定），也可用齿距偏差计算并进行圆整。

C=0.5048ln（z）-1.144ln（m_mn）+2.852ln（f_pt）+3.32 （6-27）

式中 z——小轮或大轮的齿数，用计算得C值大的齿数；

f_pt——齿廓中点的齿距偏差（μm）。

对于某种给定精度等级C系数，推荐的最大节线速度按下式确定：

式中 v_etmax——大端节圆直径的最大节线速度（图形中K_V曲线的端点处），m/s。

（5）齿向载荷系数K_Hβ、K_Fβ

1）概述

①齿向载荷系数K_Hβ、K_Fβ修正强度计算式，反映载荷沿齿宽分布的均匀性。

②K_Hβ定义为每单位齿宽的最大载荷与单位齿宽的平均载荷之比。

③K_Fβ定义为最大齿根应力与平均齿根应力之比。

④载荷不均匀分布的大小受下列因素影响：

——轮齿制造精度、轮齿接触斑点、齿距精度；

——在安装中齿轮的对中度；

——由轮齿内部载荷或外部载荷引起的轮齿、轴、轴承、箱体、支承箱体的基础的弹性变形；

——轴承公差；

——齿面赫兹接触变形；

——由于运行温度产生的热膨胀与热变形（特别对于箱体与齿轮轴、轴承的材料不同的齿轮装置特别重要）；

——由于运行速度产生的离心变形。

⑤锥齿轮的几何特征是沿着齿宽方向变化的。切向载荷的轴向分量与径向分量是随轮齿接触位置而变化的。同样，齿轮箱的安装基础变形与轮齿变形也要改变，进而影响到轮齿接触的位置、大小与形状。

对于运行转矩变化的情况，在满载下应期望有“理想”的接触，在中间载荷下，可接受满意的接触。

2）A法 为按A法精确确定载荷沿齿宽的分布，所有影响系数（例如：在使用中齿根应力的测量）都要全面的分析。然而由于其成本高，在实践中这种分析方法受到限制。

3）B法 锥齿轮的B法的方案还在研究中。

4）C法

①齿向载荷分布系数K_Hβ-C。在锥齿轮中，齿向载荷分布主要受到鼓形齿与使用中变形的影响。为考虑鼓形效果（点接触）用一椭圆代替矩形接触区，椭圆的长轴等于齿宽b，其短轴等于相应的当量圆柱齿轮端面啮合线的长度。在载荷分布的计算中，这个系数取1.5（这个值仅适应用于具有良好接触斑点的锥齿轮副）。

变形的影响与轴承布置的影响，用装配系数K_Hβ-be来考虑。K_Hβ-be的值见表6-26。

表6-26 装配系数K_Hβ-be

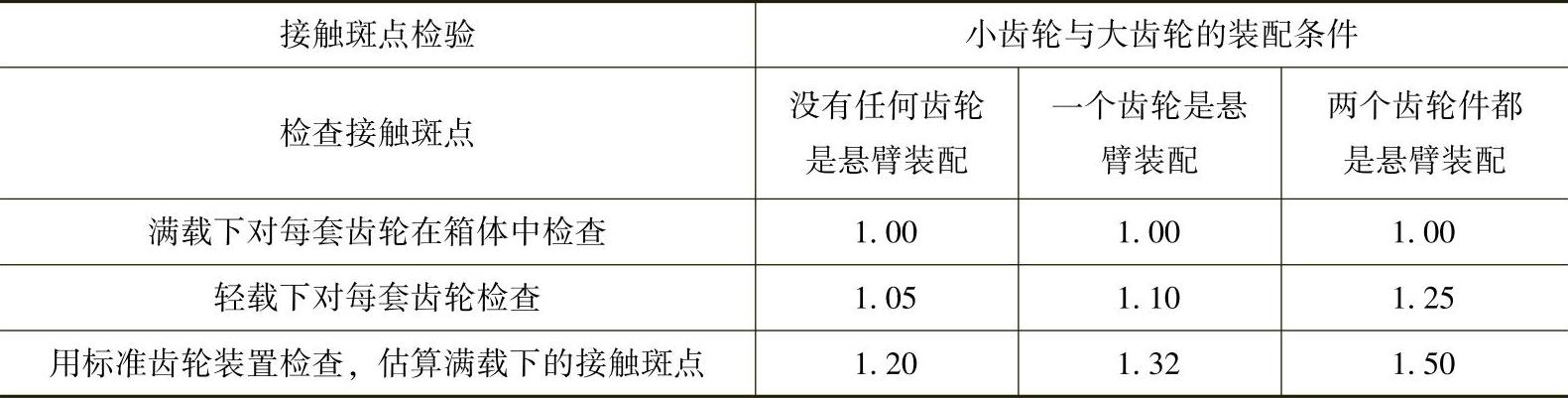
注：在最大的工作载荷下并在良好的接触斑点条件下检查，最大的工作载荷由装配条件下齿轮的变形试验证实。

为补偿在满载下有效齿宽b_e小于齿宽b的85%，齿向载荷系数要修正，则齿向载荷系数K_Hβ-C为：

对于b_e≥0.85b

对于b_e＜0.85b

上述公式对非鼓形齿不适用。

②齿向载荷分布系数K_Hβ-C。K_Fβ是考虑沿齿宽载荷分布对轮齿根部应力的影响。

K_Hβ见式（6-29）、式（6-30）；K_F0见式（6-32）、式（6-34）。

③弯曲强度的齿长曲率系数K_F0。齿长曲率系数取决于：

a）螺旋角。

b）齿长方向齿的曲率。

齿长方向曲率系数的计算公式：

对弧齿锥齿轮

式中 r_c0——刀具半径（mm）；

R_m——中点锥距（mm）。

式中 β_m——中点螺旋角。(www.daowen.com)

如果K_F0的计算值大于1.15，取K_F0=1.15；如果K_F0的计算值小于1.0，则取K_F0=1.0。

对直齿锥齿轮和零度齿锥齿轮

K_F0=1.0 （6-34）

（6）端面载荷分配系数K_Hα、K_Fα

1）概述 总的切向载荷在啮合的几对齿中（在给定的齿轮尺寸条件下）的分配取决于齿轮制造精度与总的切向载荷的数值。K_Hα考虑载荷分配对接触应力的影响，K_Fα考虑载荷分配对齿根应力的影响（更详尽的资料参看GB/T 3480—1997）。采用A法需深入的分析，但不论何种应用场合，用近似的B法和C法已足够精确。

2）A法 作为承载能力计算基础的载荷分配可由测试方法或对所有的影响系数的精确分析方法来确定。当采用分析方法时，该方法的精度与可靠度要被证实，并要明确前提条件。

3）B法

①当量圆柱齿轮的重合度ε_vγ≤2的锥齿轮

式中 c_γ——啮合刚度，其近似值c_γ=20N/（mm·μm）；

f_pt——齿距偏差，取小轮或大轮的齿距偏差的最大值；

y_a——跑合允许量；

F_mtH——分锥上齿宽中点的切向力，F_mtH

=F_mtK_AK_VK_Hβ；

K_Hα与K_Fα也可按图6-41选取。

②当量圆柱齿轮的总重合度ε_vγ＞2的锥齿轮

③边界条件。如果K_Hα与K_Fα＜1，则K_Hα与K_Fα取1。

在式（6-35）与式（6-36）中，如果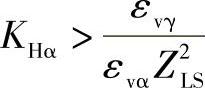，取

式中 Z_LS——载荷分担系数。

在式（6-35）与式（6-36）中，如果，取ε

式中 Y_ε——弯曲强度计算的重合度系数。

上述边界条件，已假定了最不利的载荷分布状况，即仅一对轮齿传递总的切向力，因而计算是安全的。推荐对于斜齿与弧齿锥齿轮的精度要进行选择，以使K_Hα与K_Fα不超过ε_vαn（法截面内当量圆柱齿轮的端面重合度）。

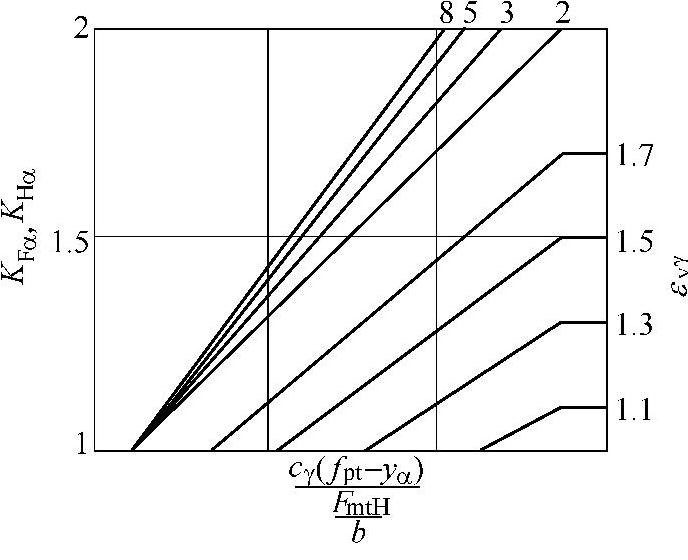
图6-41 端面载荷系数K_Hα-β、KFα-β

4）C法

①综合评述。一般来说，该法对工业齿轮是足够精确的。为确定系数K_Hα-C与K_Fα-C，必须知道齿轮精度等级、单位载荷、锥齿轮的类型和跑合特性等。跑合特性由材料与热处理来表达。

②前提条件与假定

a）端面重合度：1.2＜ε_vα＜1.9。

b）轮齿刚度值取c′=14N/（mm·μm）或c_γ=20N/（mm·μm）。

c）用齿距偏差确定每个齿轮的精度等级。按此假定，得到的端面载荷系数，对于大多数应用场合，即在平均的与较高单位载荷情况下以及单位载荷F_mtK_A/b_e＜100N/mm的情况下，该数值是偏安全的。

③系数的确定。K_Hα-C与K_Fα-C按表6^-27确定。

表6-27 端面载荷分配系数K_Hα-C与KFα-C

5）跑合允许量y_a跑合允许量y_a是使运行开始时啮合的不贴合误差减小的跑合量。如果没有直接经验，y_a可从图6-42或图6-43中选取。下列各式，代表图中各曲线，供计算时使用。

图6-42 切线速度v_mt＞10m/s的齿轮副的跑合允许量ya

结构钢与调质钢

灰铸铁

渗碳淬火钢与渗氮钢

图6-43 切线速度v_mt≤10m/s的齿轮副的跑合允许量ya

结构钢与调质钢

灰铸铁

渗碳淬火钢与渗氮钢

对调质钢

当v_mt≤5m/s时 无限制

当5m/s<v_mt≤10m/s时y_a≤12800/σ_Hlim

当v_mt＞10m/s时y_a≤6400/σ_Hlim

对灰铸铁

y_a=0.275f_pt （6-40）

当v_mt≤5m/s时 无限制

当5m/s<v_mt≤10m/s时y_a≤22μm

当v_mt>10m/s时y_a≤11μm

对渗碳淬齿轮与渗氮齿轮

y_a=0.075f_pt （6-41）

对所有速度，限制：y_a≤3μm。

大轮与小轮材料不同时：

y_a1按小齿轮材料确定，y_a2按大齿轮材料确定。

（7）锥齿轮几何参数计算

这里所包含的几何参数是展成当量圆柱齿轮和锥齿轮承载能力计算所需的。如果将锥齿轮的轮齿中间的端截面展成为一个平面，则得到近似渐开线齿的当量圆柱齿轮，GB/T 10062承载能力计算是在当量圆柱齿轮和锥齿轮齿宽中点的基础上进行的。

对于斜齿和弧齿锥齿轮，其当量齿轮是当量圆柱斜齿轮。在承载能力计算中，一部分在齿轮的端截面内进行，一部分在其法截面内进行。所提供的齿轮数据的对应关系仅适用于x_hm1+x_hm2=0的齿轮。

1）原始数据 锥齿轮的数据可用下述两种常用形式中的任意一种：数据形式Ⅰ（见表6-28）与数据形式Ⅱ（见表6-29）。

表6-28 数据形式Ⅰ

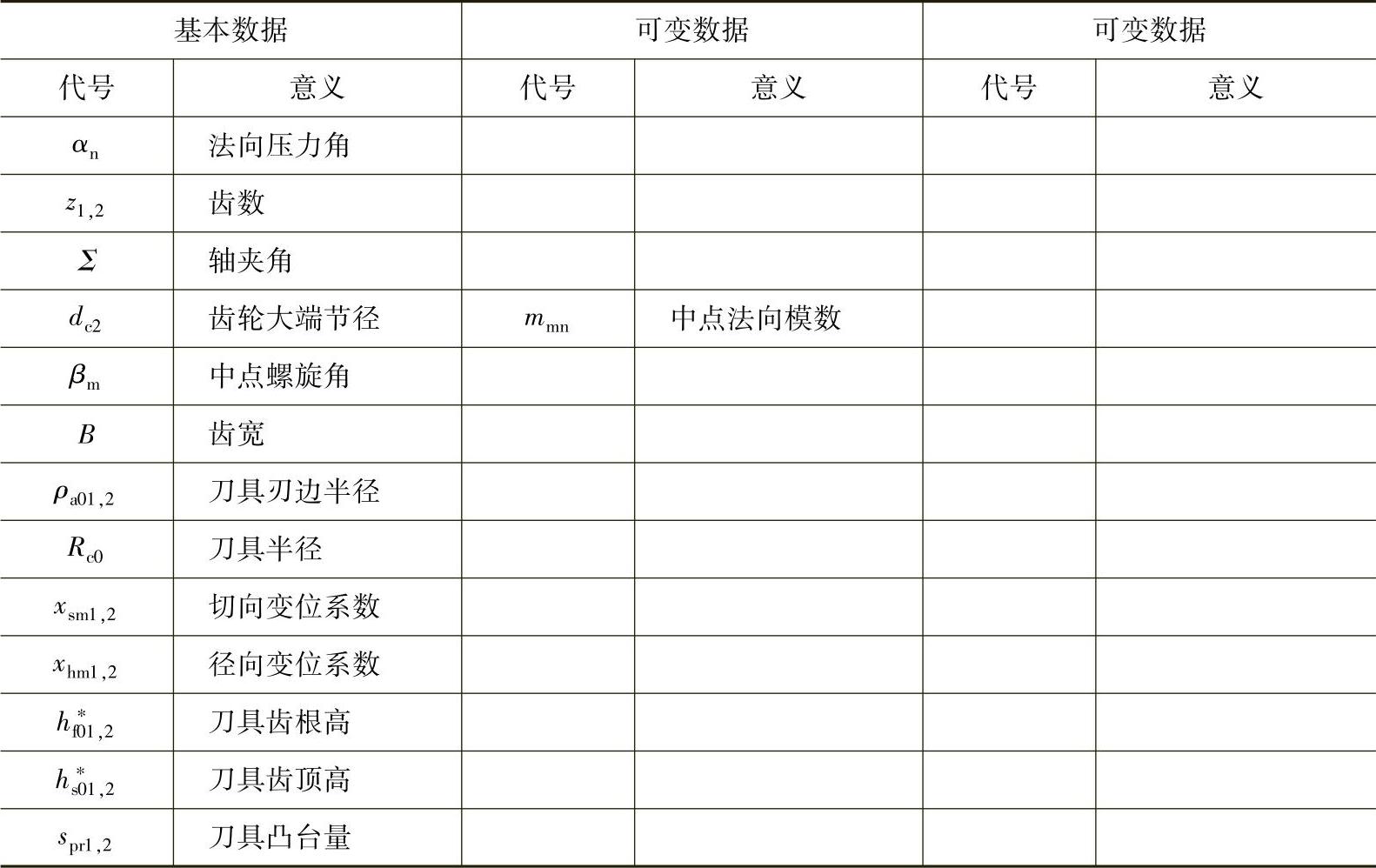
表6-29 数据形式Ⅱ

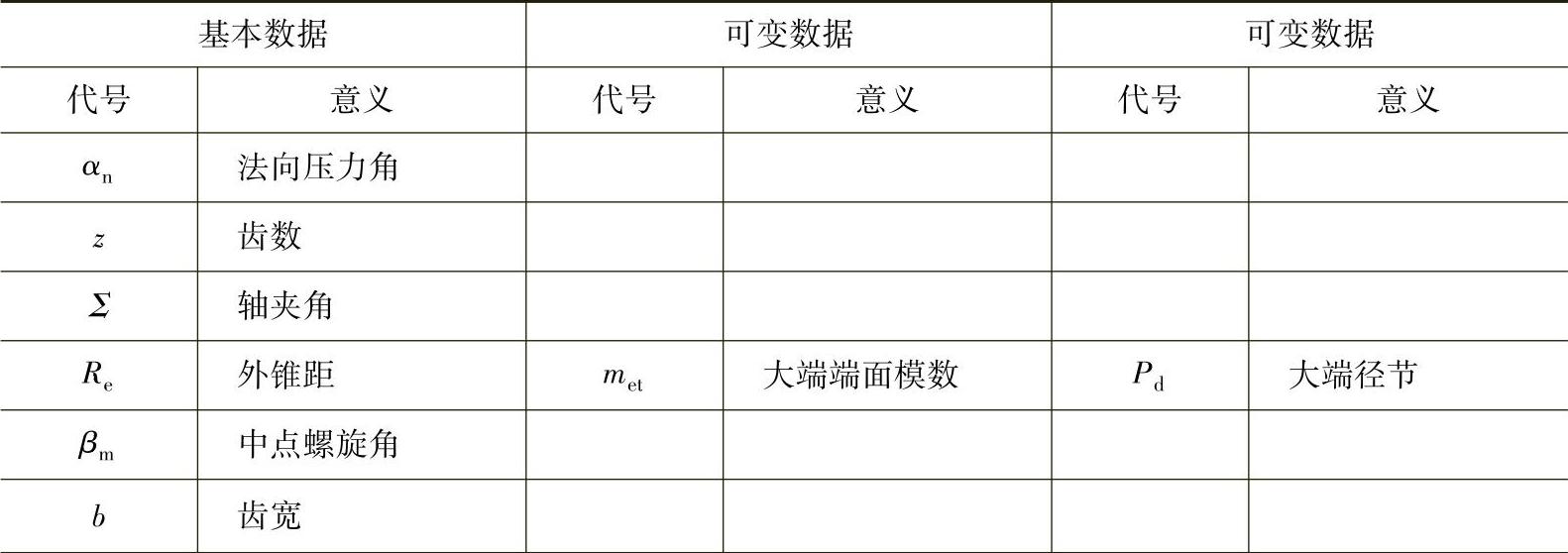
（续）

2）基本计算式

齿数比u

节锥角δ

外锥距Re

中点锥距Rm

大端端面模数met

中点端面模数mmt

中点法向模数m_mn

m_mn=m_mtcosβ_m （6-51）

中点节圆直径dm

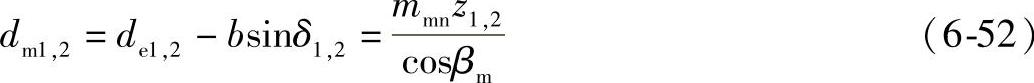
齿顶角θ_a

θ_a1，2=δ_a1，2-δ_1，2 （6-53）

对于固定的齿顶高

δ_a1，2=δ1，2➝θ_a1，2=0 （6-54）

齿根角θ_f

θ_f1，2=δ₁，2-δ_f1，2 （6-55）

对于固定的齿顶高

δ_f1，2=δ1，2➝θf1，2=0 （6-56）

3）基本齿条齿廓及其相应的刀具的数据 在表6-28的数据形式Ⅰ中，一般来说，

h_f0、h_a0与ρ_a0可由制造者自己确定。

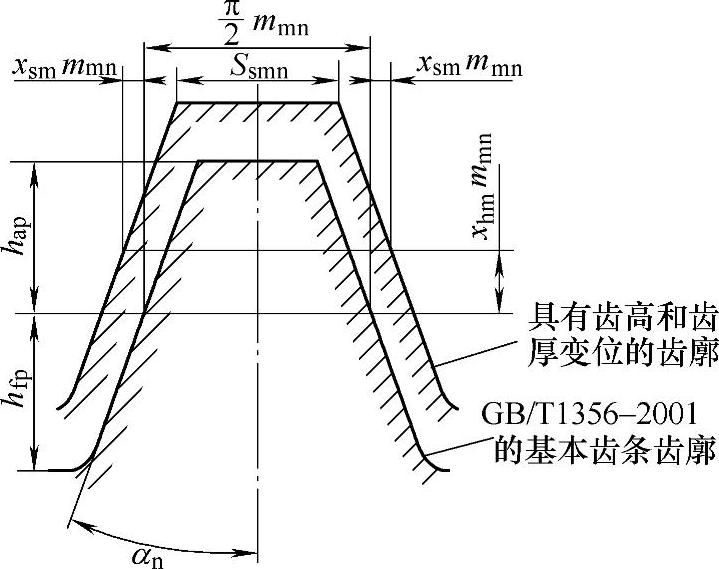
图6-44 基本齿条齿廓

刀具齿根高h^*_f0（即基本齿条齿廓齿顶高h^*_ap，见图6-44）与中点法向模数有关：

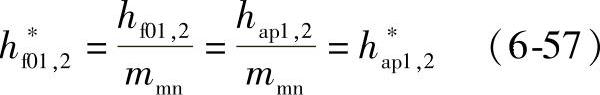
刀具齿顶高（即基本齿条齿廓齿根高

h^*_fp，见图6-44）与中点法向模数有关：

常用数值：

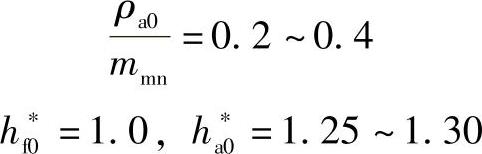
在数据形式Ⅱ（表6-29）中，仅表示了刀具刃边半径ρ_a0。如果需要，h_f0*与h_a*0可计算得出。

4）中点齿高

①中点齿高

中点齿顶高ham

中点齿根高hfm

②在数据形式Ⅱ（表6-29）中

中点齿顶高ham

中点齿根高h_fm

径向变位系数x_hm

5）当量圆柱齿轮在端面的数据（下标v）在图6-45中，对于当量圆柱齿轮的各几何参量，不用下标m（m通常表示齿面中点处）表示。

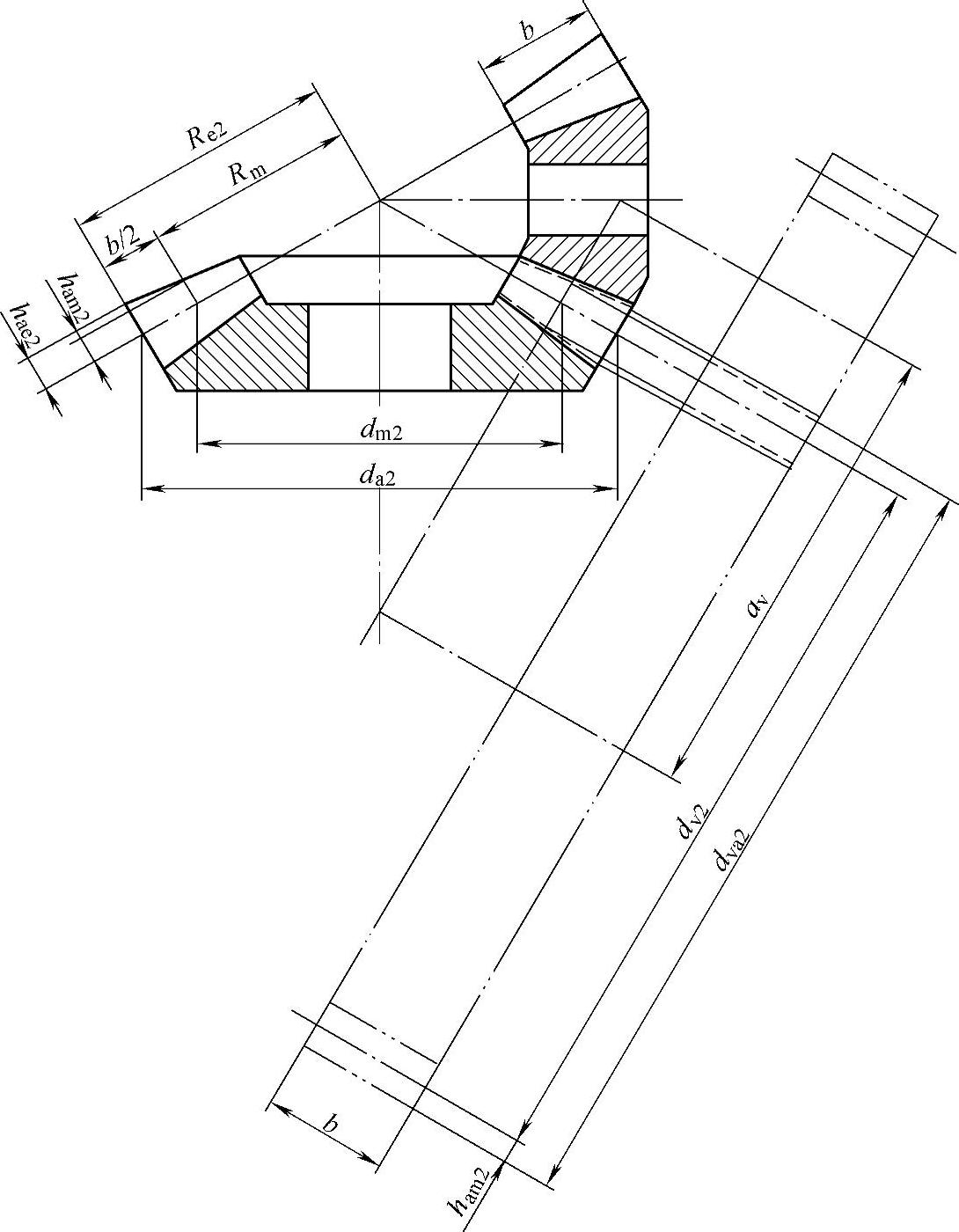
图6-45 当量圆柱齿轮的计算参量

齿数z_v

对于Σ=90°

齿数比uv

对于Σ=90°

分度圆直径dv

对于Σ=90°

d_v2=u²d_v1 （6-71）

中心距av

顶圆直径d_va

d_va1，2=dv1，2+2h_am1，2 （6-73）

基圆直径dvb

基圆螺旋角β_vb

β_vb=arcsin（sinβ_mcosα_n） （6-76）

端面基节p_et

p_et=m_mtπcosα_vt （6-77）

啮合线长度gva

端面重合度εvd

纵向重合度εvβ

按式（6-79）与式（6-80）算出的当量圆柱齿轮的重合度，对承载能力的计算是重要的。但上述重合度可能偏离按锥齿轮实际尺寸算得的重合度。

修正的重合度ε_vγ

由于锥齿轮的齿是鼓形的，所以设定：接触区为一椭圆，其长轴的长度等于齿宽。当轮齿的接触已恰当扩展后，满载时轮齿的接触不应超过椭圆的边界。

接触线的长度l_b：

图6-46表示计算接触线长度值的一般定义。

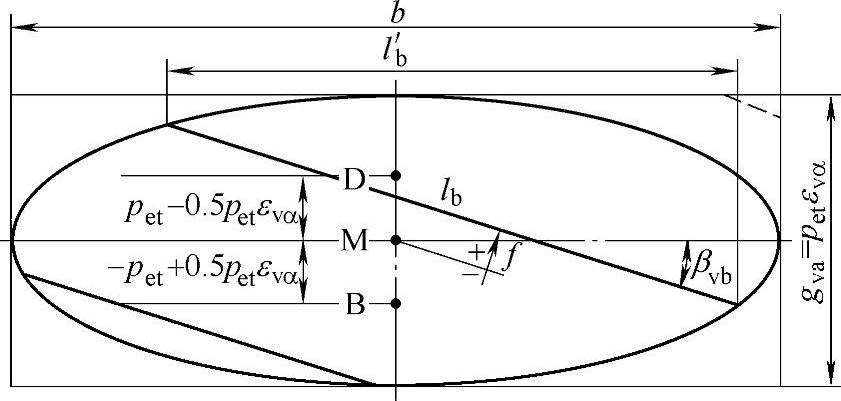
图6-46 接触线长度的一般定义

B—单对齿啮合内界点

D—单对齿啮合外界点

式（6-82）和式（6-83）按表6-30计算：

a）齿顶接触线按f=f_t。

b）齿中部接触线按f=f_m。

c）齿根接触线按f=f_r。

表6-30 啮合区的齿顶、齿中部、齿根接触线的距离f

齿中间接触线的长度也可按下述方式表示：

对于ε_vβ＜1

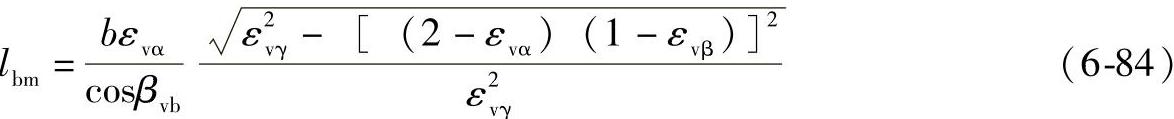
对于ε_vβ≥1

齿中部接触线的投影长度l_bm

l′_bm=l_bmcosβ_vb （6-86）

6）当量圆柱齿轮法截面的几何参数（下标vn）

齿数zvn

分度圆直径dvn

中心距avn

顶圆直径d_van

d_van1，2=d_vn1，2+d_va1，2-dv1，2=d_vn1，2+2h_am1，2 （6-92）

基圆直径d_vbn

d_vbn1，2=dvn1，2cosα_n=z_vn1，2m_mncosα_n （6-93）

啮合线长度gvan

重合度εvαn

7）切向变位 切向变位系数x_sm是对齿宽中点处的法向模数而言的。与ISO 53的基齿条齿廓比较，齿厚的变位量等于2x_smm_mn（见图6-44）。

a）从给出的中点法向齿顶厚度s_amn（见图6-47）计算。

载荷作用角α_Fan（见图6-59）

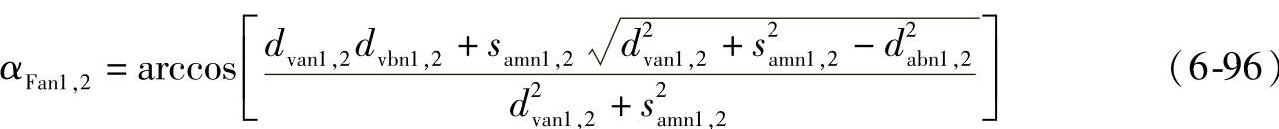
中点法向弧齿厚smn

齿厚变位系数x_sm（见图6-44）

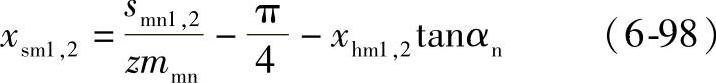
b）从给出的齿厚计算（考虑到齿厚一部分用大端表示，一部分用中点表示）。

中点端面弧齿厚smt

中点法向弧齿厚s_mnsamnsinα^Fan=dvancosα^Fan-d^vbn

s_mn1，2=s_mt1，2cosβ_m （6-100）

齿厚变位系数x_sm按式（6-98）计算。

图6-47ef24 中点法向齿顶厚

（8）使用系数K_A

1）使用系数的确定 使用系数K_A最好能用使用经验的全面分析方法按一定的使用条件来确定。如果缺乏使用经验，必须进行全面分析研究。

2）使用系数的近似值 如果缺乏使用经验或详细的分析无法实现，表6-31提供了使用系数的典型值。

注：必须细心地使用表6-31，因在某些应用场合K_A值会很高（已使用过的K_A值高达10）。

由于锥齿轮常设计成长的（对小轮）或短的齿顶高的齿，而不论小轮或大轮哪个是主动件，当大轮为主动件时这将引起节点前啮合。因此，增速传动的使用系数值要比减速传动的大。

表6-31 使用系数K_A值

注：表中数值适用于减速传动。对增速传动，用表中的K_A值再加0.01u²，u=z₂/z₁。

（9）接触斑点

将轮齿的接触斑点调整至所期望的形状和位置的方法称为轮齿接触扩展方法。该方法是用大轮和小轮的位移控制接触斑点，接触检查在锥齿轮试验机上进行，齿轮在一合理速度下运转并加一轻载荷。

在试验机上位移在三个方向进行：

——沿小齿轮轴线；

——沿大齿轮轴线；

——垂直于大、小齿轮轴线。

试验机位移量（使接触斑点达到期望的位置）等量用于切齿或磨齿机床的安装调整中，使齿轮箱内装配好的齿轮处于合理位置并获得理想的接触斑点。在接触斑点扩展完成前，必须进行反复的试验。

当设计是一种全新的设计时，齿轮装配的轮齿接触检查和变形检查要反复进行，以加速轮齿接触的扩展和评定齿轮装配后的稳定性。在上述的试验中，齿轮箱在25%的载荷下直至满载下运转。运转速度较低，允许使用着色涂料，并读取每一次载荷下的位移量。

为确定切齿机床、磨齿机床所需的调整量，在锥齿轮试验机上相同的方向测量位移，试验机上的位移要移植到加工机床上。

因齿轮使用时要承受热变形，齿轮箱用灯泡加热至工作温度，在相同载荷下反复进行试验。各试验数据的比较表明了热膨胀率差异的影响。

接触的情况及接触的名词术语见图6-48～图6-50。

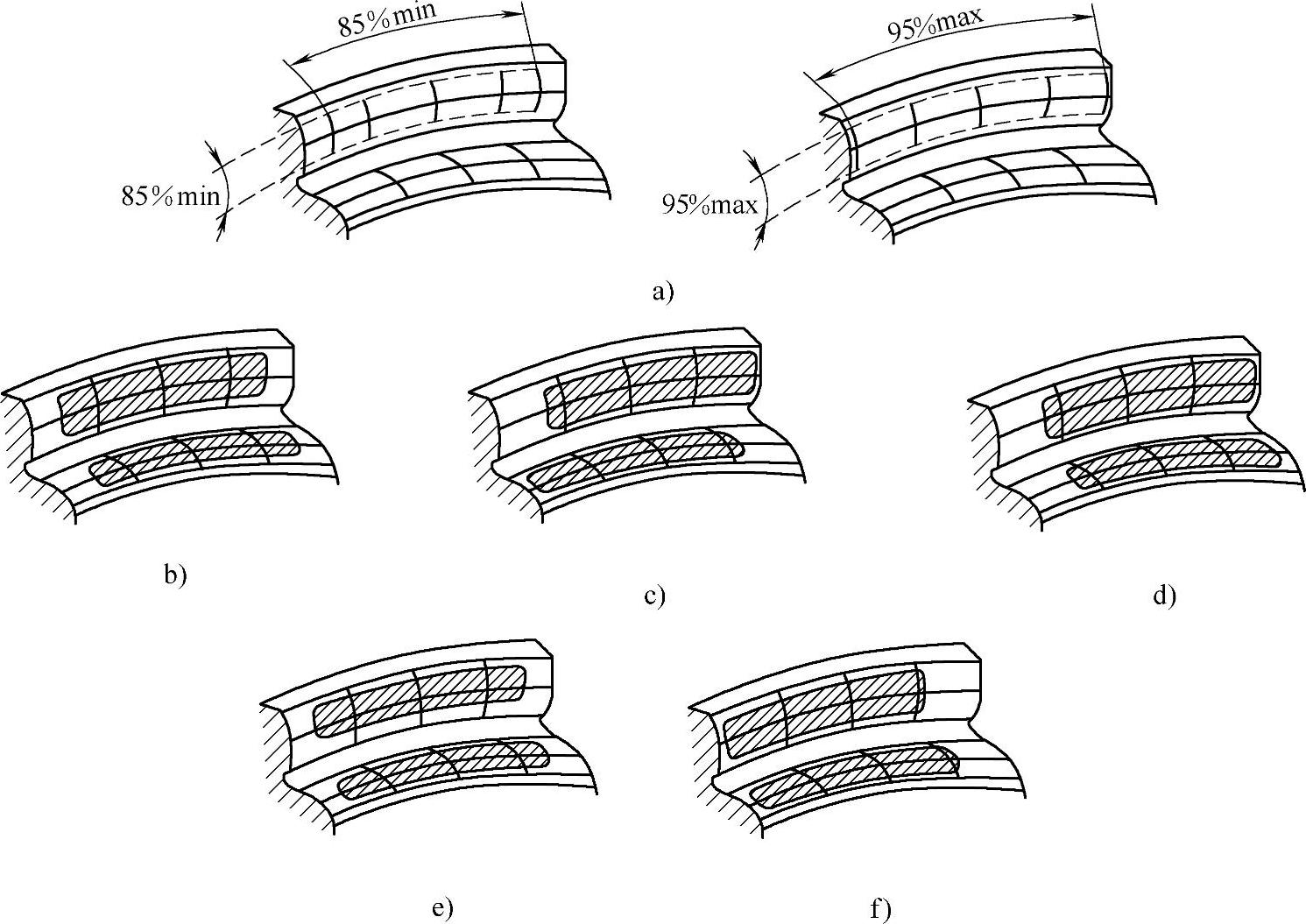
图6-48 典型的受载下的良好接触

a）设计载荷下的接触区 b）理想的接触区80%～85%（齿长），齿顶齿端修形，无偏载 c）轻微交叉接触，80%～85%接触区 d）轻微偏大端接触，80%～85%接触区 e）轻微坡形接触，80%～85%接触区 f）轻微偏小端接触，80%～85%接触区

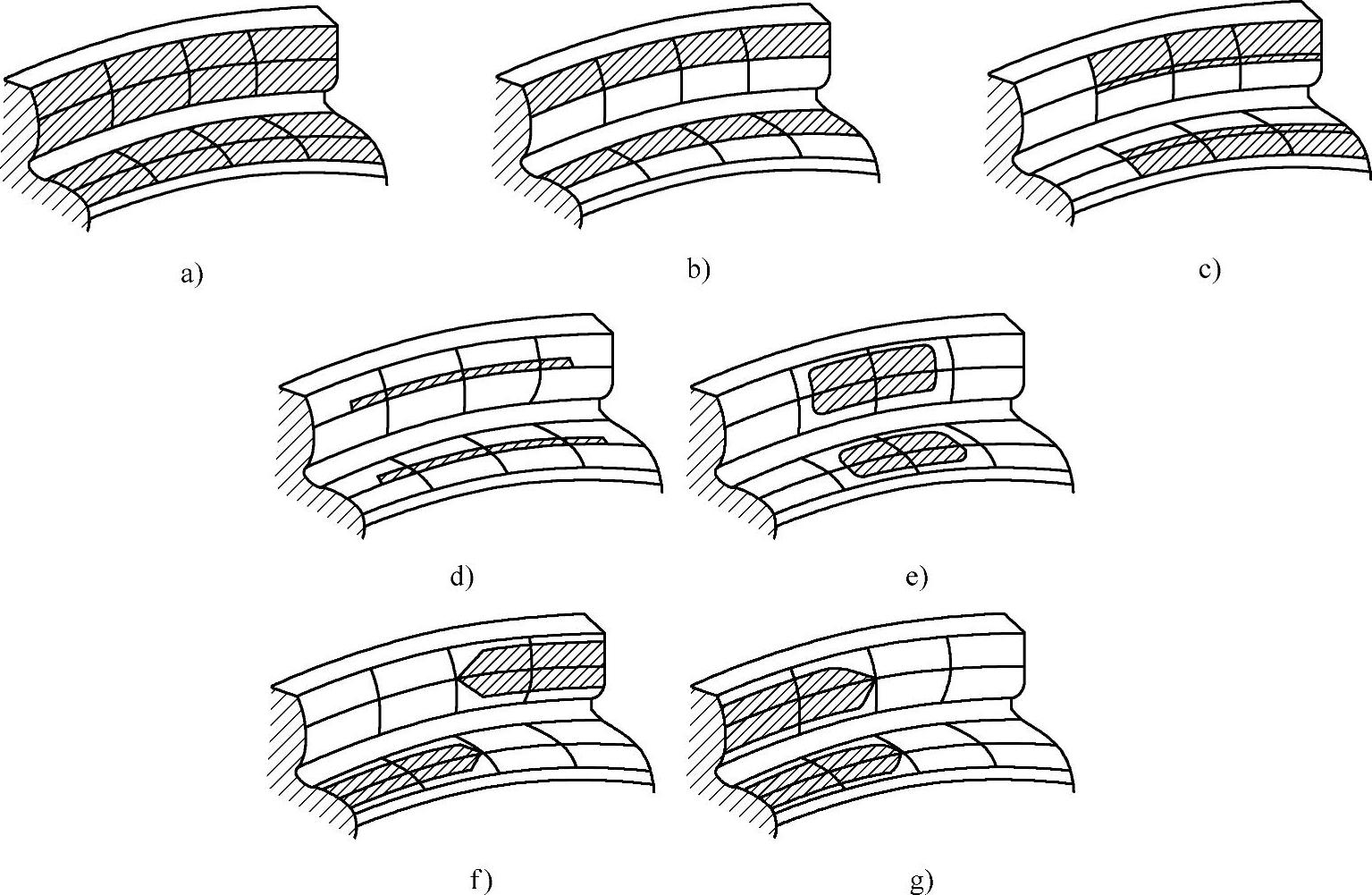
图6-49 典型的受载下的不良接触

a）全齿宽、全齿高接触、齿顶齿端无修形 b）坡形接触（一侧高，另一侧低） c）大端齿接触偏高 d）齿廓修缘过多的接触 e）齿长倒坡过多的接触 f）交叉接触（大端在一边，小端在另一边） g）齿的两面偏小端接触

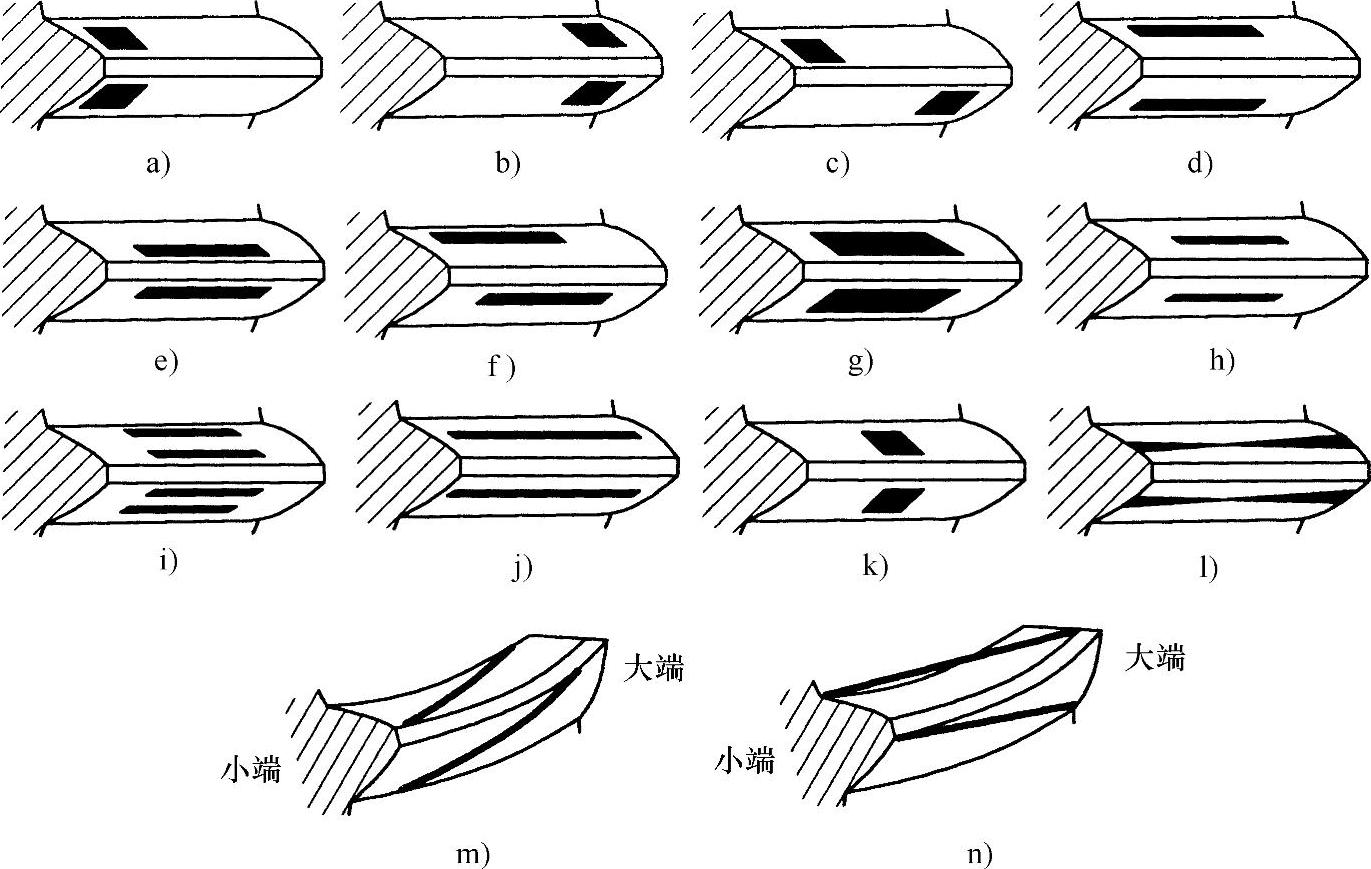
图6-50 锥齿轮接触的名词术语

a）小端接触 b）大端接触 c）交叉接触 d）低接触 e）高接触 f）坡形接触 g）宽接触 h）窄接触（节线） i）桥形接触（齿高方向） j）长接触（全齿长） k）短接触 l）桥形接触（齿长方向） m）偏内接触 n）偏外接触