HG型准双曲面齿轮：设计和制造优化策略

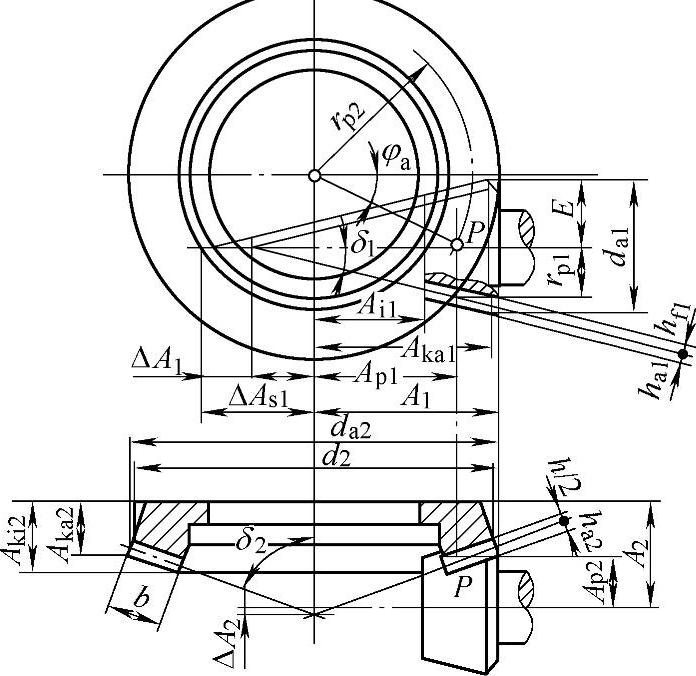
图6-35 HG型准双曲面齿轮的尺寸

HG型准双曲面齿轮用于偏置距较大的情况，即用于E＜0.208d₂及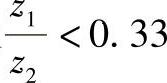的情况。HG型齿轮的偏置距可以比HN型的大40%。此种齿轮不能用标准的EN型刀盘切齿，要用EHN刀盘。HG型准双曲面齿轮的尺寸见图6-35，几何计算如下：

1）初选大轮分锥角δ₂按公式cot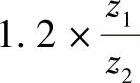δ₂=求出δ₂。

2）初算ΔA₂值按公式ΔA₂≈-0.072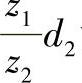计算。

3）确定A_ka1及A_i1尺寸小轮齿宽比大轮齿宽b大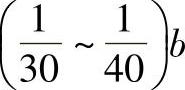，以确定A_ka1及A_i1。

4）确定大轮参考点处的分度圆半径rP2

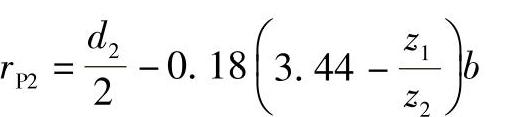
根据载荷的大小，r_P2可比计算值减小。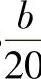

5）第一次试算

①确定小轮放大系数K。当β_P1=50°时，由图6-36根据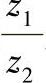r及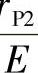查得K₅₀值。当βP1≠50°时，用下式计算K：

K=tanβ_P1sinφ′_P+cosφ′_P

式中 φ_P′=50°-β′_P2；β′_P2=β₂′=arccos（0.6428K₅₀）。

②确定_η。由图6-37根据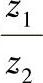及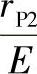查出_η值。η值增加则r′_b减少，即刀盘名义半径减小。(https://www.daowen.com)

6）第二次试算 如果第一次试算β_P1与要求的数值相差太大，就要用算得的sinφ和cosφ代入K值公式中，算出新的K值。进一步试算r′_b。第一次计算的r′_b往往与r″_b值不一致，要用新的tanη值重算。可以用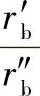乘以旧的tanη值，以其积作为新的tanη值进行第二次试算。

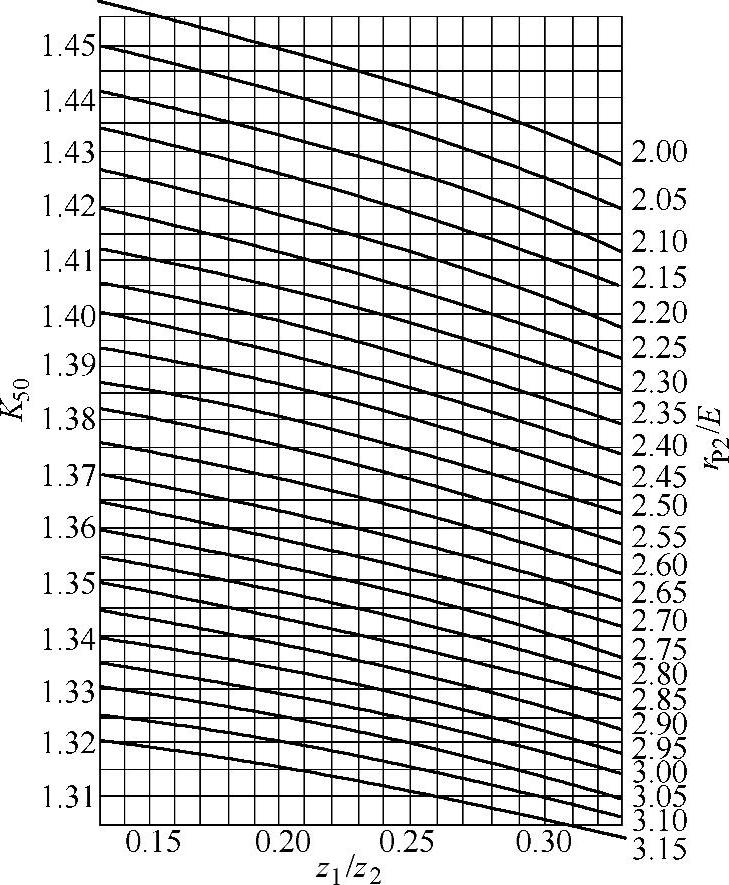
图6-3 HG型准双曲面齿轮的K值

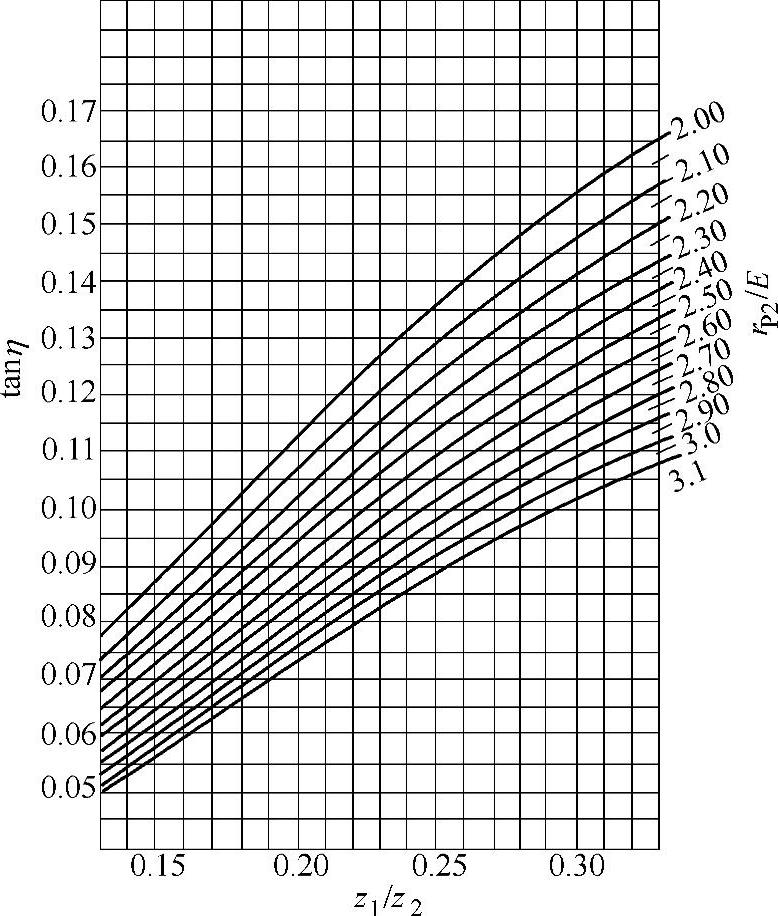
图6-37 HG型准双曲面齿轮的tanη值

HG型准双曲面齿轮几何计算见表6-19。

表6-19 HG型准双曲面齿轮几何计算 （单位：mm）

（续）

（续）