均载机构有多种类型，如弹性元件的均载机构、基本构件浮动的均载机构、杠杆联动的均载机构等。而各种类型又有多种形式。

（1）弹性元件的均载机构

它是依靠构件的弹性变形来达到载荷均衡的。载荷的不均匀系数与弹性元件的刚度和制造总误差成正比。为此采用图4-4所示，将轴做成细长型，当l很大时，由于结构刚度很小，可使太阳轮a产生径向位移，促使星轮间的载荷平均分配。

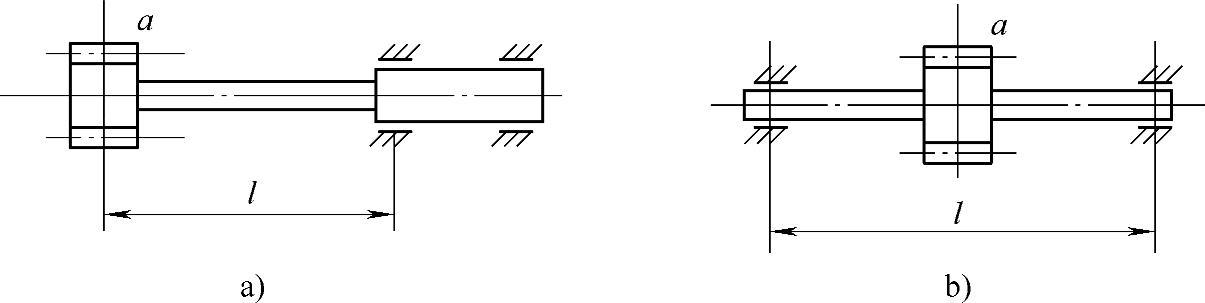
图4-4 采用轴的变形产生径向位移

以ε_max表示太阳轮可能产生的最大径向位移值，则发生这个位移值（即梁的挠度）所需要的力P可计算得出。

1）当太阳轮a悬臂式布置时（图4-4a）

式中 E——轴的弹性模量；

J——轴的惯矩。

这种情况下，ε_max与轴的偏角θ的关系为

这偏角θ使载荷沿齿宽方向分布不均匀。

2）当太阳轮a简支式布置时（图4-4b）

这种情况下，ε_max与轴的偏角θ的关系为

这时虽载荷沿齿宽方向分布均匀了，但要达到ε_max位移所需的力P增大了。这种均载机构需要传动装置轴向尺寸较大，因此往往会遇到由于轴向尺寸的限制而不宜采用。

（2）杠杆联动的均载机构

它是借杠杆联动机构使星轮浮动，达到均载目的。采用这种机构，星轮个数可以N_p≥3，有利于提高传动装置的承载能力。其缺点是结构较为复杂，零件数量较多。图4-5为一个4星轮浮动的均载机构，从图4-6可见，杠杆的平衡条件为

P₁L₁=Pe(www.daowen.com)

P₂L₂=Pe

十字槽形盘的平衡条件为

P₁s₁=P₂s₂

故星轮间载荷平衡条件为

式中 P——星轮负载；

e——枢轴偏心距；

s₁、s₂——分布在同一直径上的两滚子间的距离；

L₁——作用力P₁到杠杆中心A₁间的距离；

L₂——作用力P₂到杠杆中心A₂间的距离；

P₁、P₂——不同杠杆与十字槽形盘间的作用力。

（3）基本构件浮动的均载机构

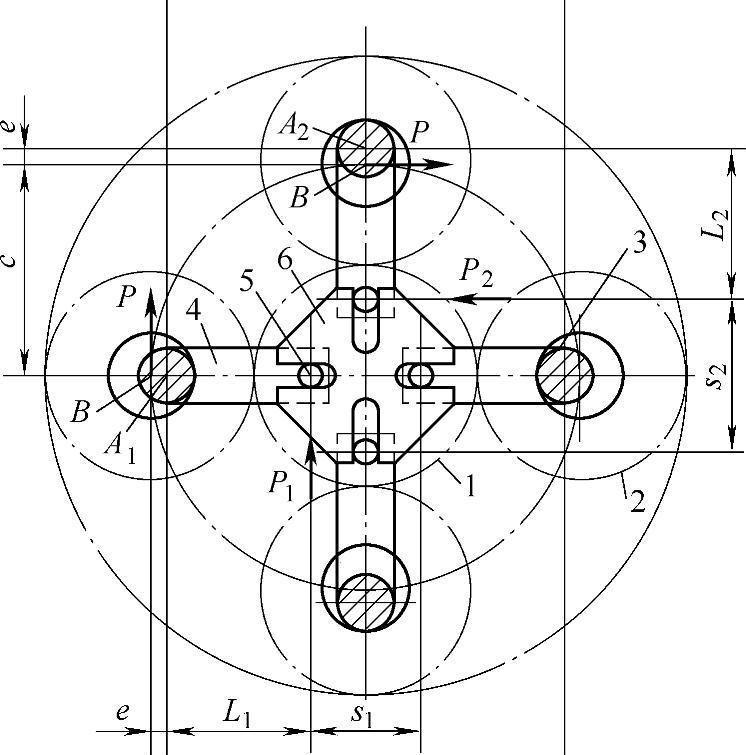
图4-54 星轮浮动的均载机构

1—太阳轮 2—星轮 3—偏心枢轴 4—杠杆 （转臂） 5—滚子 6—十字槽形盘

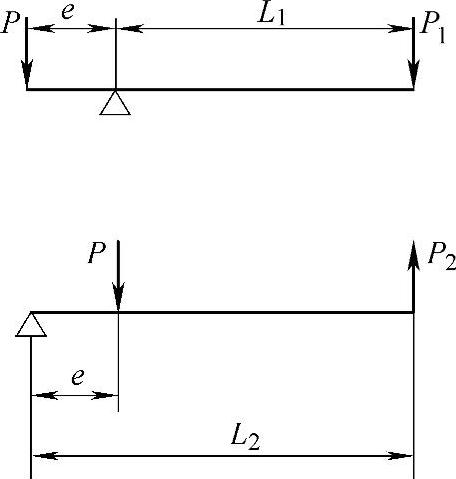
图4-6 杠杆受力图

在星形齿轮传动中，很少以星轮作为浮动构件，通常以太阳轮（或内齿圈）作为浮动构件。它具有不额外增加构件，结构简单紧凑，均载效果较好，系统可靠性高，对构件无过高精度要求等优点。所谓基本构件浮动的均载机构，是指浮动构件没有径向支承，允许其无约束地位移，当数个星轮受载不均匀时，就会引起浮动件移动，直至数个星轮载荷趋于均匀分配为止。这种均载机构在星轮数为3的轮系中应用最广，均载效果最好，其浮动件通常采用中心轮（太阳轮或内齿圈）。由图4-7可见，3个自动定心的星轮互成120°，在轮系传递动力过程中，若浮动件处于平衡时，则3个法向啮合力必构成封闭的等边三角形，从而使星轮载荷趋向均匀，达到均载目的。

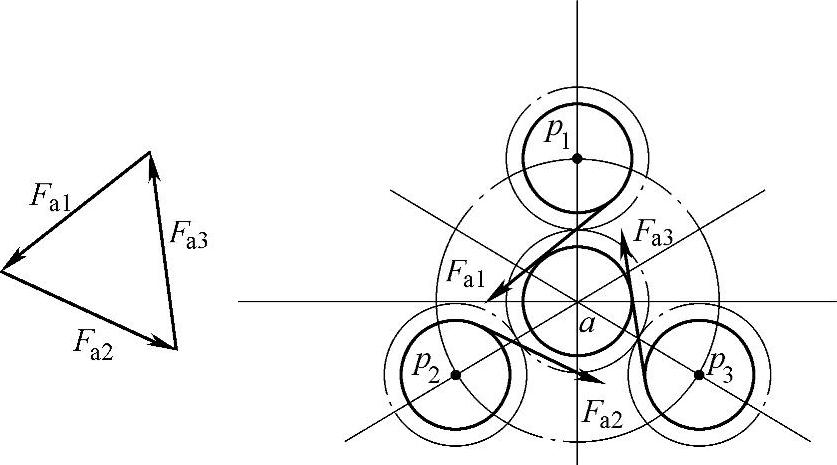
图4-7 太阳轮浮动