1881年赫兹（Hertz）应用牛顿势函数，推导出两弹性圆柱体接触区表面最大接触应力的计算公式。推导中的前提和假设条件是：两圆柱体为无限长的、均质的、各向同性的弹性体；其变形后的接触面与圆柱表面相比是极其微小的；作用力为静载荷，与接触面垂直，且沿圆柱体的长度方向均匀分布（这就可以简化为平面应力、应变分析）。

如图3-48a所示，长度为L，半径为ρ₁、ρ₂的两平行圆柱体在加载前为线接触，当加上法向力F之后，接触处变形成一个宽度为2s的矩形面积。取其某一截面进行应力分析（图3-48b），则作用于该截面上的法向力，即为F/L。在该截面上的应力呈椭圆分布：

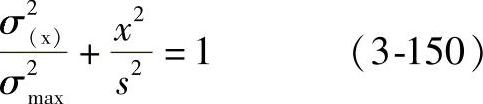
即

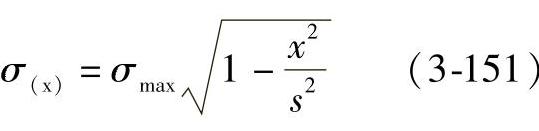
则在该截面内，作用在2s宽度上的应力之和，就是这半个椭圆的面积：

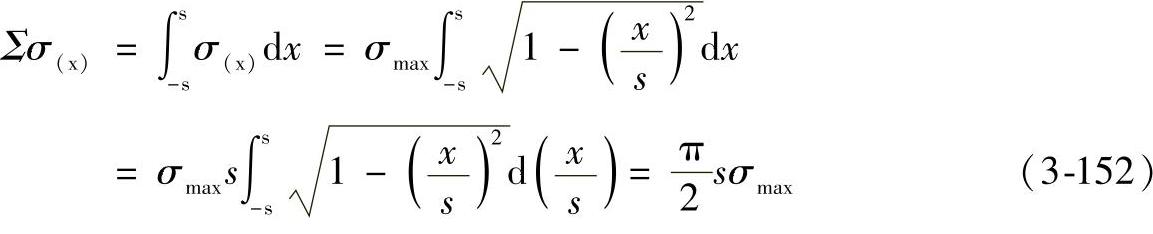
已知，此时作用在该截面内的法向力F/L应与Σσ（x）相等，即

则最大压应力为

又根据弹性力学可知，接触变形宽度的一半为

(www.daowen.com)

将式（3-155）代入式（3-154），可得出

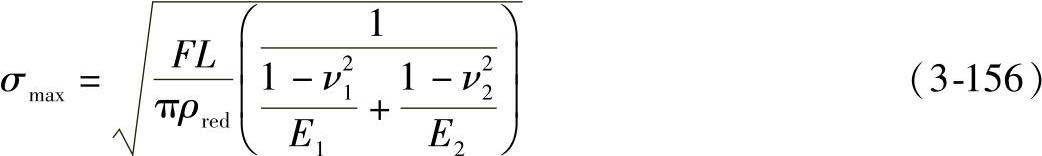
式中 ν₁、ν₂——圆柱体1、2材料的泊松比，对于钢通常ν=0.3；

E₁、E₂——圆柱体1、2材料的弹性模量，对于钢通常E=2.1×10⁵ MPa；

ρ_red=ρ1ρ2——当量曲率半径；

ρ₂+ρ₁

ρ₁、ρ2——两圆柱体的曲率半径；

F/L——作用在圆柱体单位长度上的法向力。

式（3-156）即为接触应力赫兹公式的一般表达式。其计算σ_max称为赫兹应力（即接触应力）。

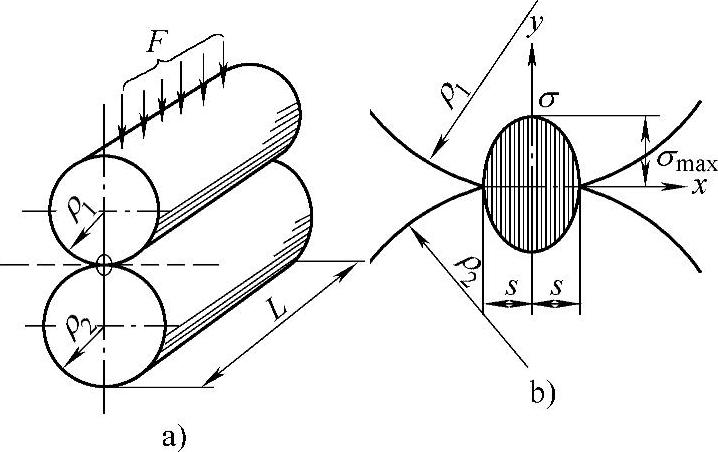
图3-48 轮齿接触应力的分布与计算