（1）过载系数K_O

允许具体齿轮承受大于名义切向载荷F_t的外载荷。只有取得大量的实际应用经验后，某一使用场合下的过载系数才能很好地确定。

在本计算方法中，K_O=1包含了有限次数下200%过载循环（典型的情况是8h内发生少于4次过载，每个峰值持续时间不超过1s）。更大瞬时载荷或频繁过载需要另外处理。

确定过载系数时，需要考虑到这样的事实：许多驱动机和工作机在单独或联合工作时产生的瞬时尖峰载荷显著大于根据驱动机或工作机计算的名义载荷。应该考虑过载的许多来源，有些是：系统振动，加速度转矩，超速，系统操作变化，多驱动机工作时功率分流时各分路的不均匀分享，以及工作载荷在过程中的变化。

（2）动载系数K_v

动载系数K_v考虑因轮齿内部非共轭啮合运动而导致的轮齿载荷。其定义如下：

式中，F_d是因传动误差引起的动力响应载荷增量，不包括传递的切向载荷。如果不能精确计算或测量，可以用图3-30查得K_v的值。图中A_v是传动精度等级，可以近似地当作相关的齿轮精度等级A，主要考虑节距和轮廓偏差。齿轮精度等级定义见ANSI/AG_- MA 2015-1-A01标准。传动精度等级在6以下被认为是非常精确的齿轮，K_v值在1.0和1.1之间。

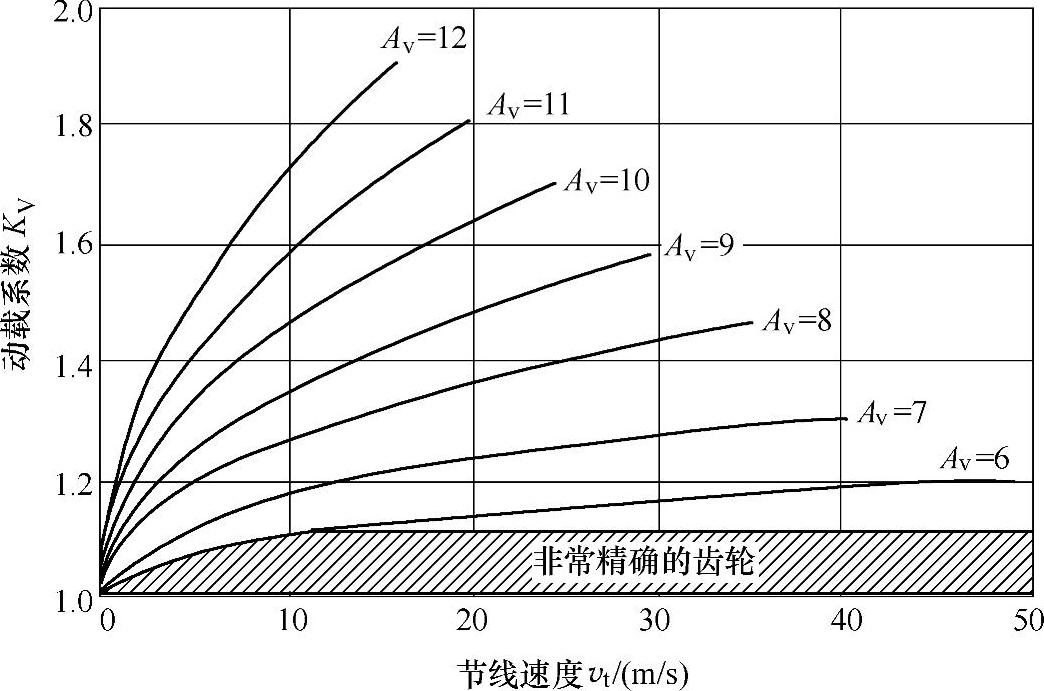
图3-30 动载荷系数Kv

（3）载荷分布系数K_H

载荷分布系数包括：①齿宽载荷分布系数K_Hβ；②端面载荷分布系数K_Hα。如果写成函数的形式，则有

K_H=f（K_Hβ，K_Hα） （3-57）

K_Hα考虑几个齿同时啮合时，各个齿分担的载荷不均匀的情况。K_Hα在本计算方法中可以假定为1。这样，

K_H=K_Hβ （3-58）

K_Hβ考虑载荷在同一齿上沿齿宽方向不均匀分布的情况。K_Hβ的值等于最大的载荷密度（接触应力）除以平均载荷密度。K_Hβ的值可以用经验公式或解析方法计算。经验公式适用于刚度较高的齿轮设计并且满足如下要求：

1）啮合齿宽与节圆直径比，b/d_w1≤2.0（如果是双斜齿轮，齿宽不计两斜齿中间空隙的距离）。

2）齿轮受对称轴承支承。

3）最大齿宽是1020mm。

4）沿全齿宽接触（接触斑迹覆盖全齿宽）。

本计算方法使用的经验公式如下：

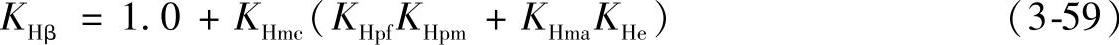
式中 K_Hmc——齿向修正系数；

K_Hpf——小齿轮比例系数；

K_Hpm——小齿轮比例修正系数；

K_Hma——啮合偏差系数；

K_He——啮合偏差修正系数。

1）齿向修正系数K_Hmc，修正因齿向修正改变最大载荷密度：

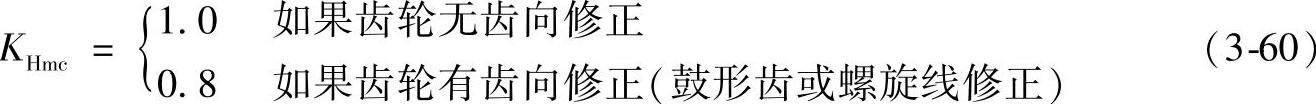
2）小齿轮比例系数K_Hpf，考虑载荷作用下的变形。这些变形往往和齿宽成比例。K_Hpf的值可从图3-31查得或通过下列方程求出：

当b≤25mm，

当25mm<b≤432mm，

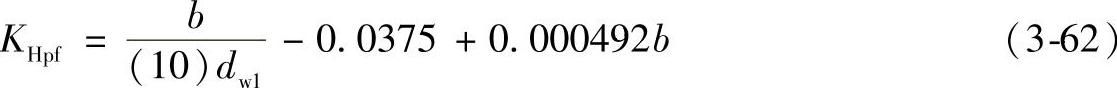
当432mm<b≤1020mm，

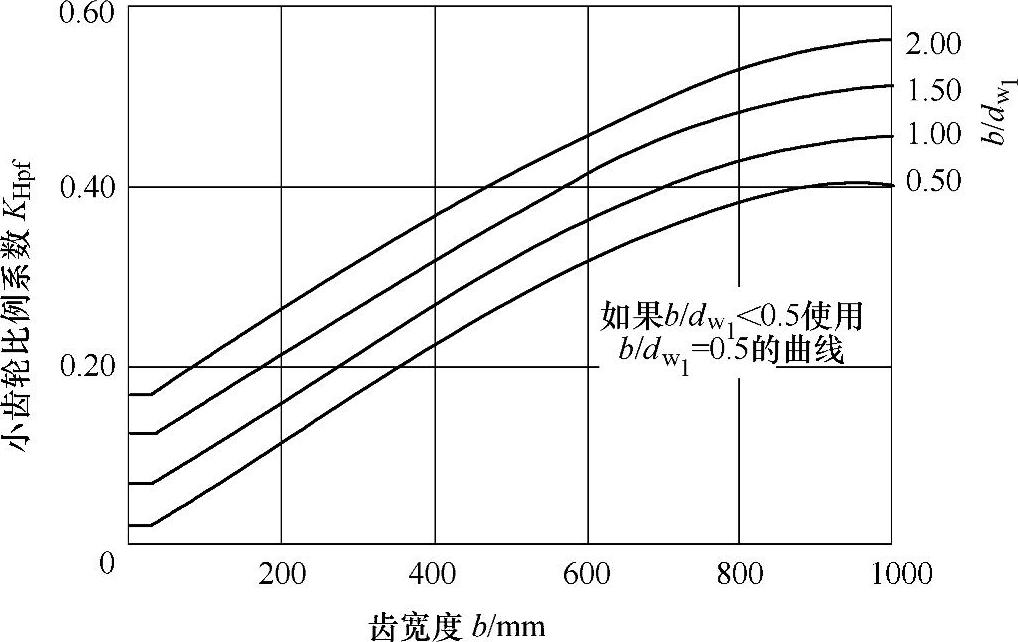
图3-31 小齿轮比例系数KHpf

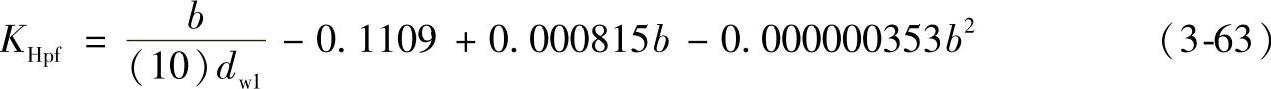
注意，如果b/d_w1<0.5，取b/d_w1=0.5代入式（3-61）～式（3-63）计算。

3）小齿轮比例修正系数K_Hpm，根据小齿轮相对于轴承中心线的位置，见图3-32，修正系数K_Hpm：

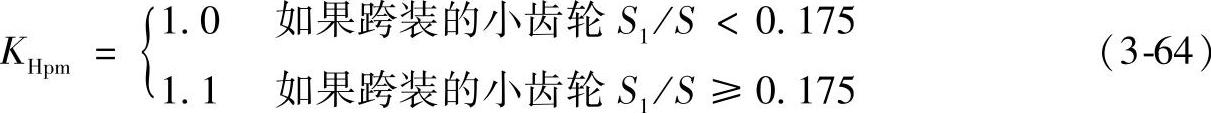
式中 S₁——偏心距，即齿宽中心和轴承跨度中点的距离；

S——轴承跨度。

4）啮合偏差系数K_Hma，考虑除弹性变形外其他因素造成的对应两齿轮的两啮合节圆柱旋转轴的偏差。啮合偏差系数的值可以从图3-33查得。对于相斜齿轮，齿宽b取实际啮合齿宽一半的值。

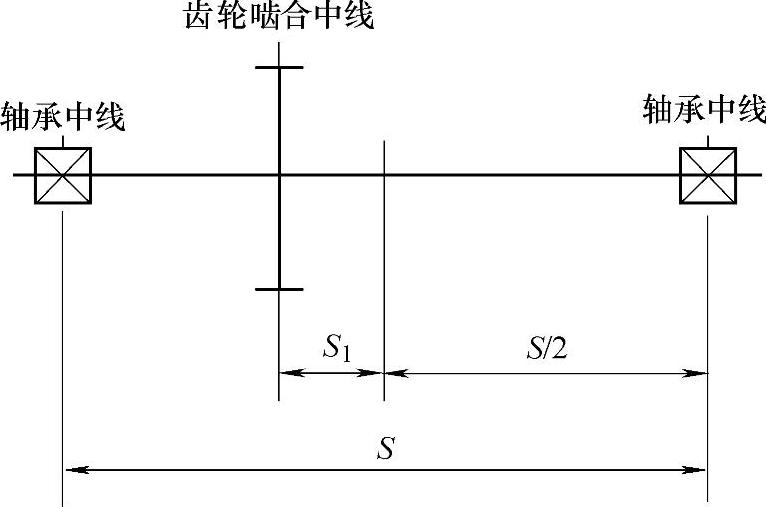
图3-32 S和S₁的估算

图3-33中各曲线是通过下列方程计算的：

K_Hma=A+B（b）+C（b）2（3-65）

式中，A、B和C的值见表3-13。

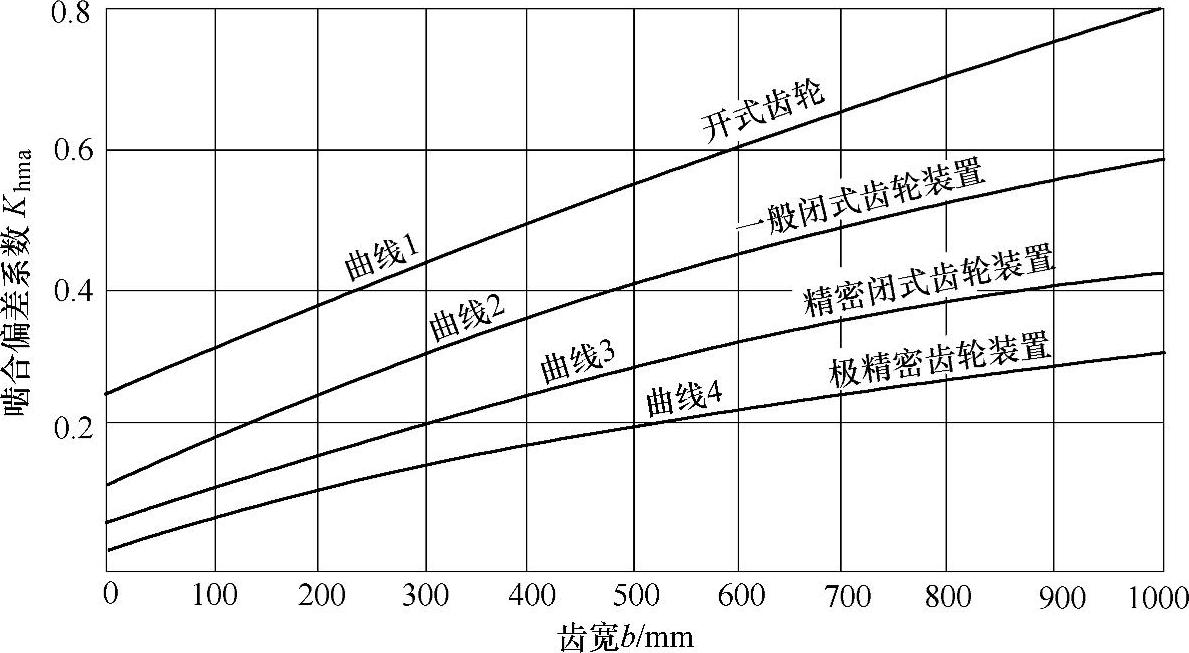
图3-33 啮合偏差系数KHma

表3-13 经验系数A、B和C

5）啮合偏差修正系数K_He，根据是否有制造或安装措施改善啮合偏差，修正系数K_He：

（4）弹性系数ZE

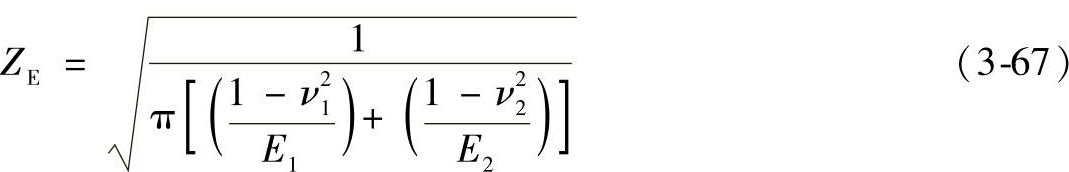
式中 ν₁、ν₂——小齿轮和大齿轮的泊松比；

E₁、E2——小齿轮和大齿轮的弹性模量。

例如对于钢齿轮，ν₁=ν₂=0.3，E₁=E₂=2.05×10⁵MPa，Z_E=190MPa。

（5）轮缘厚度系数K_B

考虑当齿轮轮缘变得很薄时计算的弯曲应力要修正。K_B随轮缘厚度的变化见图3_-34。图中的横坐标m_B称作支撑率，由下式定义：

式中 t_R——从齿根往下测量的轮缘厚度（mm）；

h_t——全齿高（mm）。

当m_B≥1.2时，K_B=1。

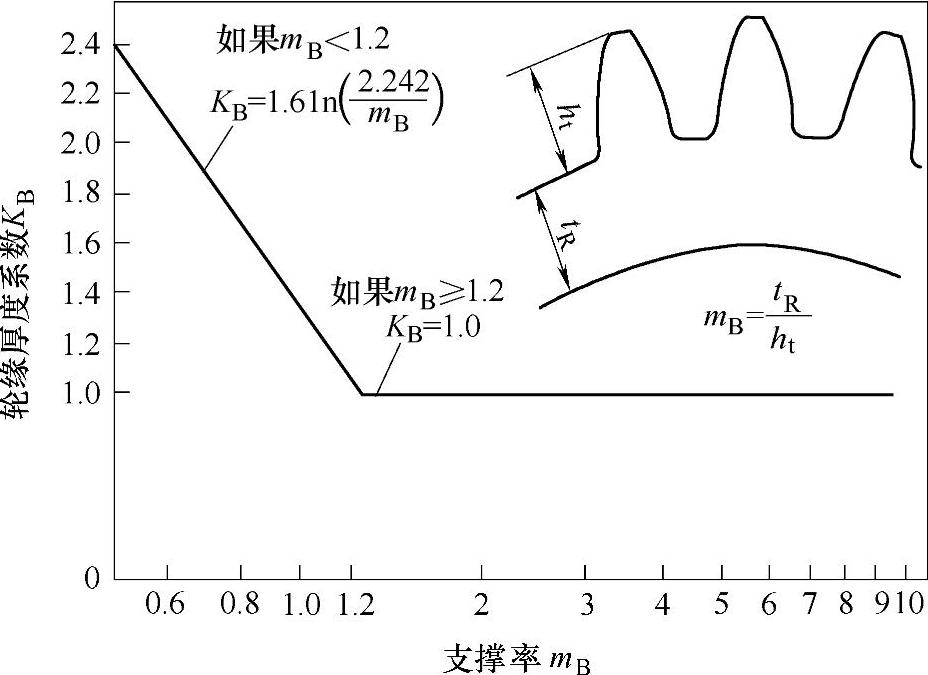
图3-3 4轮缘厚度系数KB

（6）应力循环系数Z_N和Y_N

根据设计要求的工作循环次数分别修正许用接触应力σ_Hp和许用弯曲应力σ_Fp。在不同的载荷循环次数n_L下，Z_N和Y_N的值分别查图3-35和图3-36。在AGMA标准中，载荷或应力循环次数n_L被定义为在单向载荷作用下被分析轮齿的啮合次数。

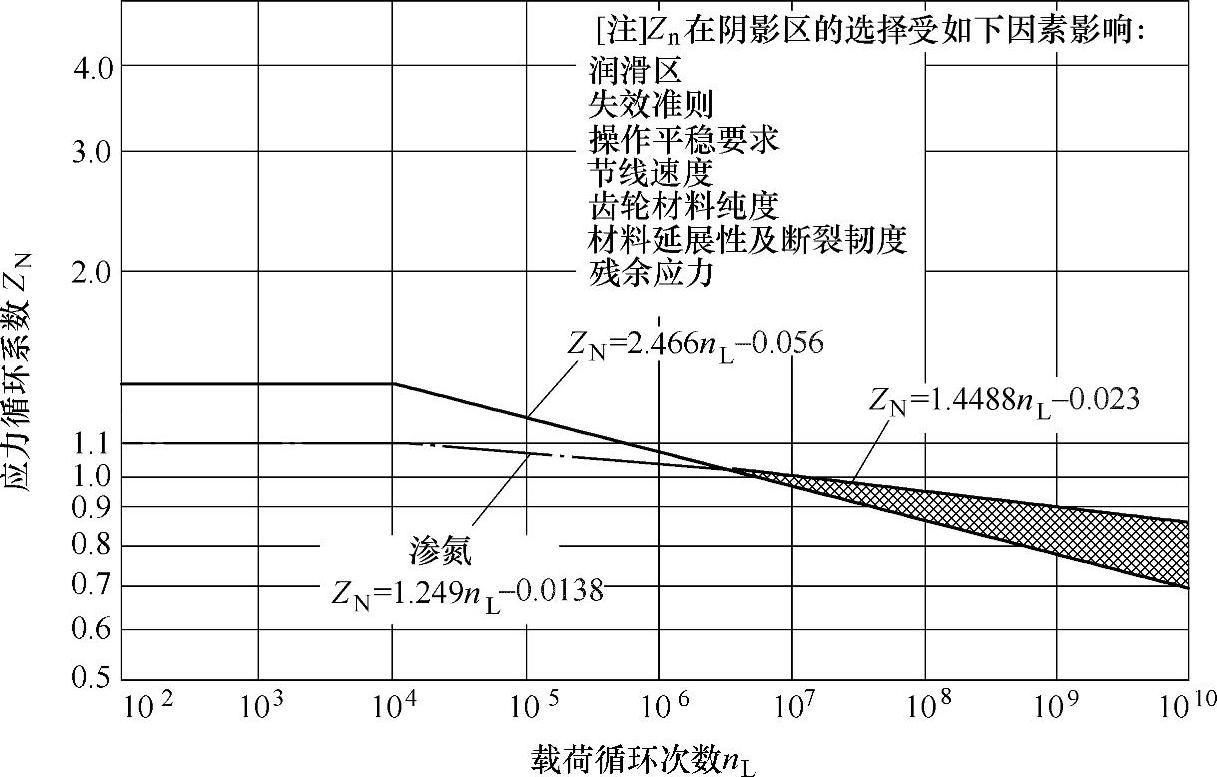
图3-35 抗点蚀的应力循环系数Z_N

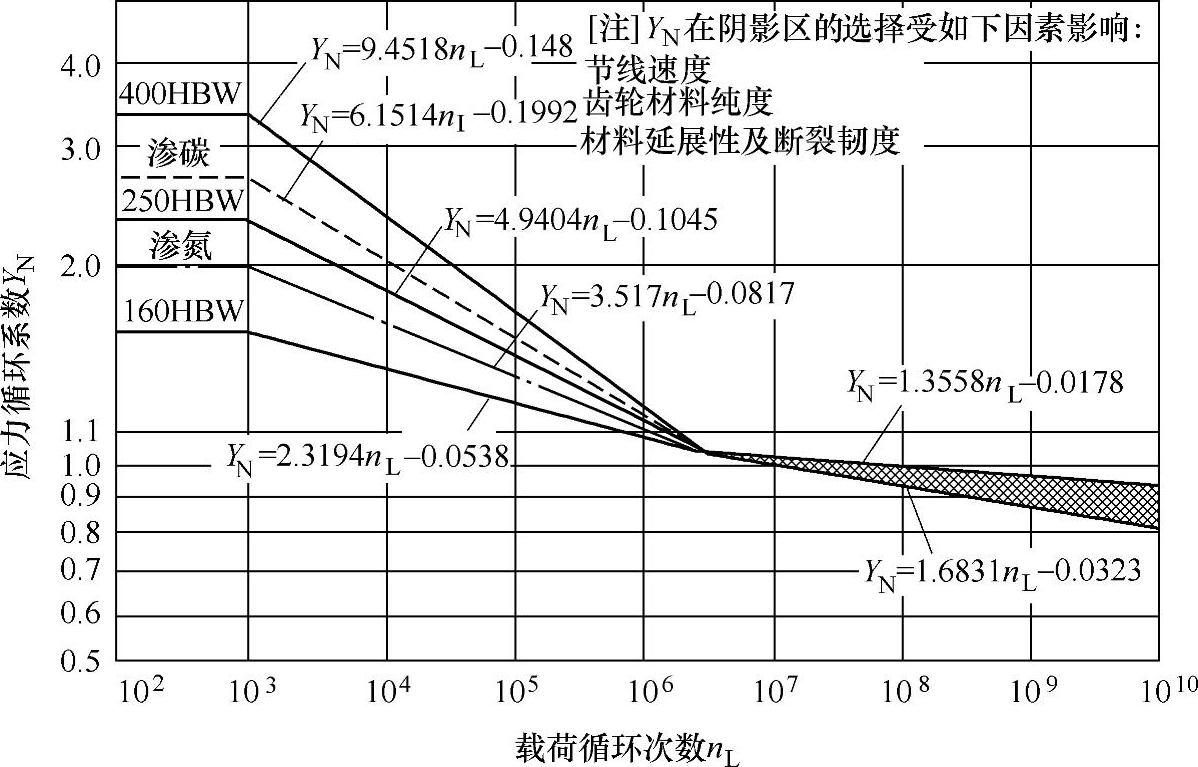
图3-36 弯曲强度应力循环系数Y_N

（7）抗点蚀的工作硬化系数Z_W

取决于：①速比；②小齿轮表面粗糙度；③小齿轮和大齿轮的硬度。小齿轮的Z_W值总为1。大齿轮的Z_W值要么是1或查图3-37或图3-38。

（8）可靠性系数Y_Z

考虑材料强度试验时失效成统计理论中的正态分布特征。表3-12中的许用应力σ_HP和σ_FP是基于10⁷载荷循环下百分之一的失效概率。要求不同的失效概率时，可用表3-14给出的可靠性系数修正许用应力。这些数据原是提供给美国海军用于弯曲和点蚀失效。

表3-14 可靠性系数Y_Z

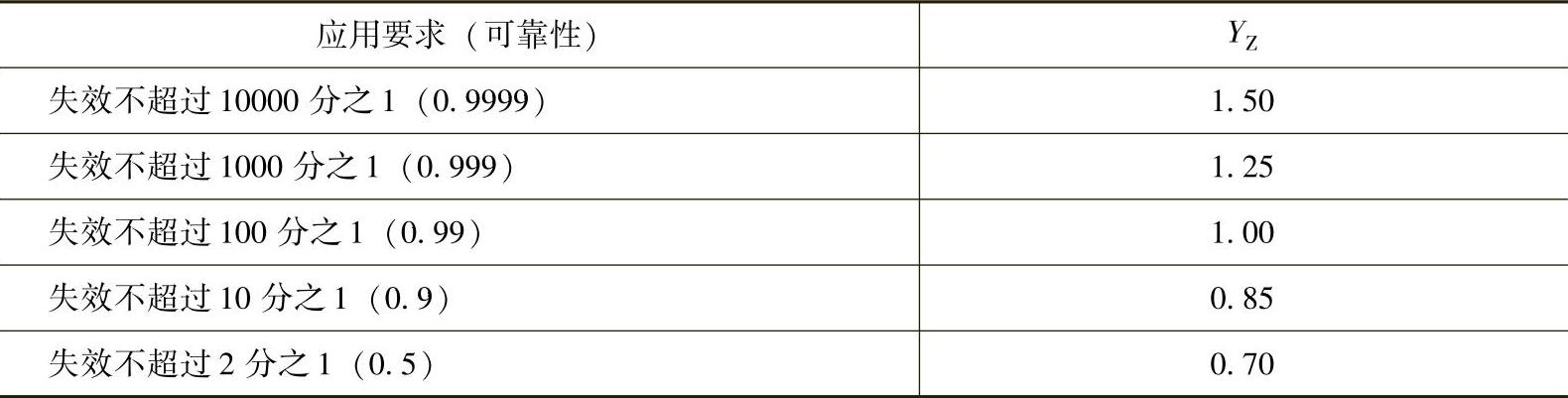
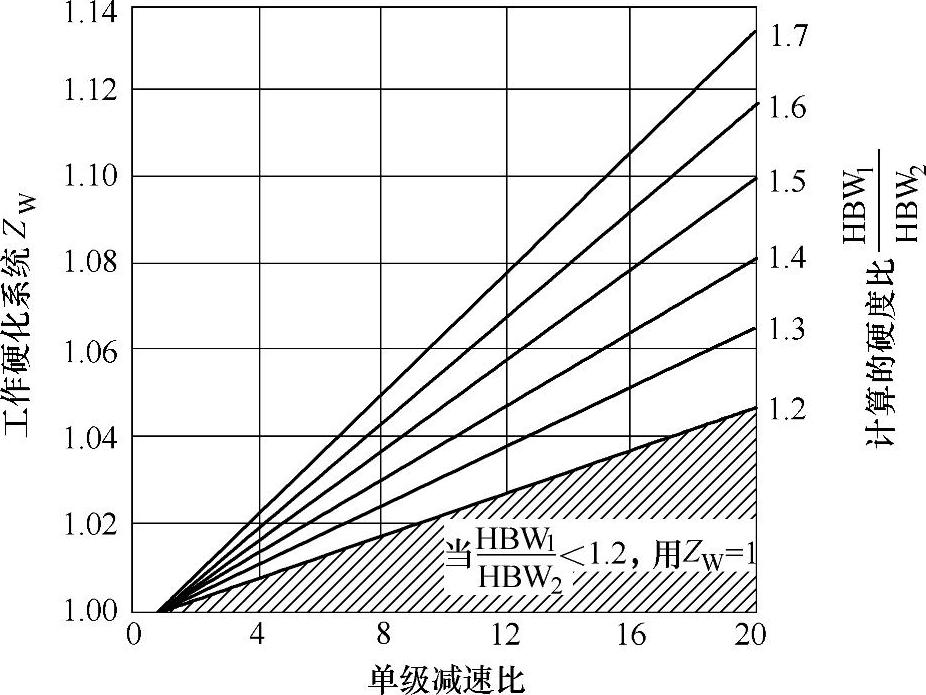
图3-37 工作硬化系数Z_W（调质）

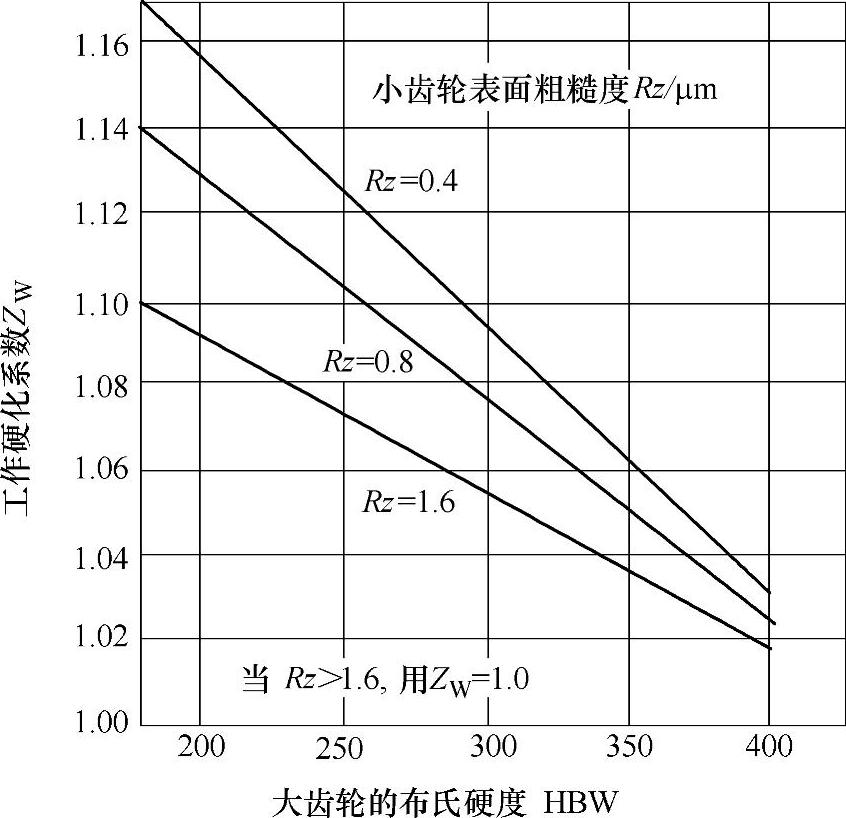
图3-38 工作硬化系数Z_W（表面硬化的小齿轮）

如果应用要求（可靠性）和表中列出的不完全重合，可选用如下的插值公式：

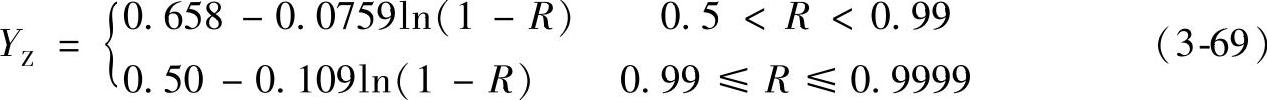
式中 R——可靠性。

（9）许用接触应力σ_HP和许用弯曲应力σ_FP

其值随材料成分、纯度、残余应力、微观结构、质量、热处理及加工工艺而变化。表3-15～表3-18及图3-39～图3-42给出了经过实验室试验或现场实践经验积累得出的许用接触应力和许用弯曲应力。这些数据基于过载系数为1、应力循环次数为10⁷、单向受载及可靠性为99%。对于惰轮或完全双向受载的齿轮，许用弯曲应力应为以上σ_FP的70%。

表3-15 钢齿轮的许用接触应力σHP

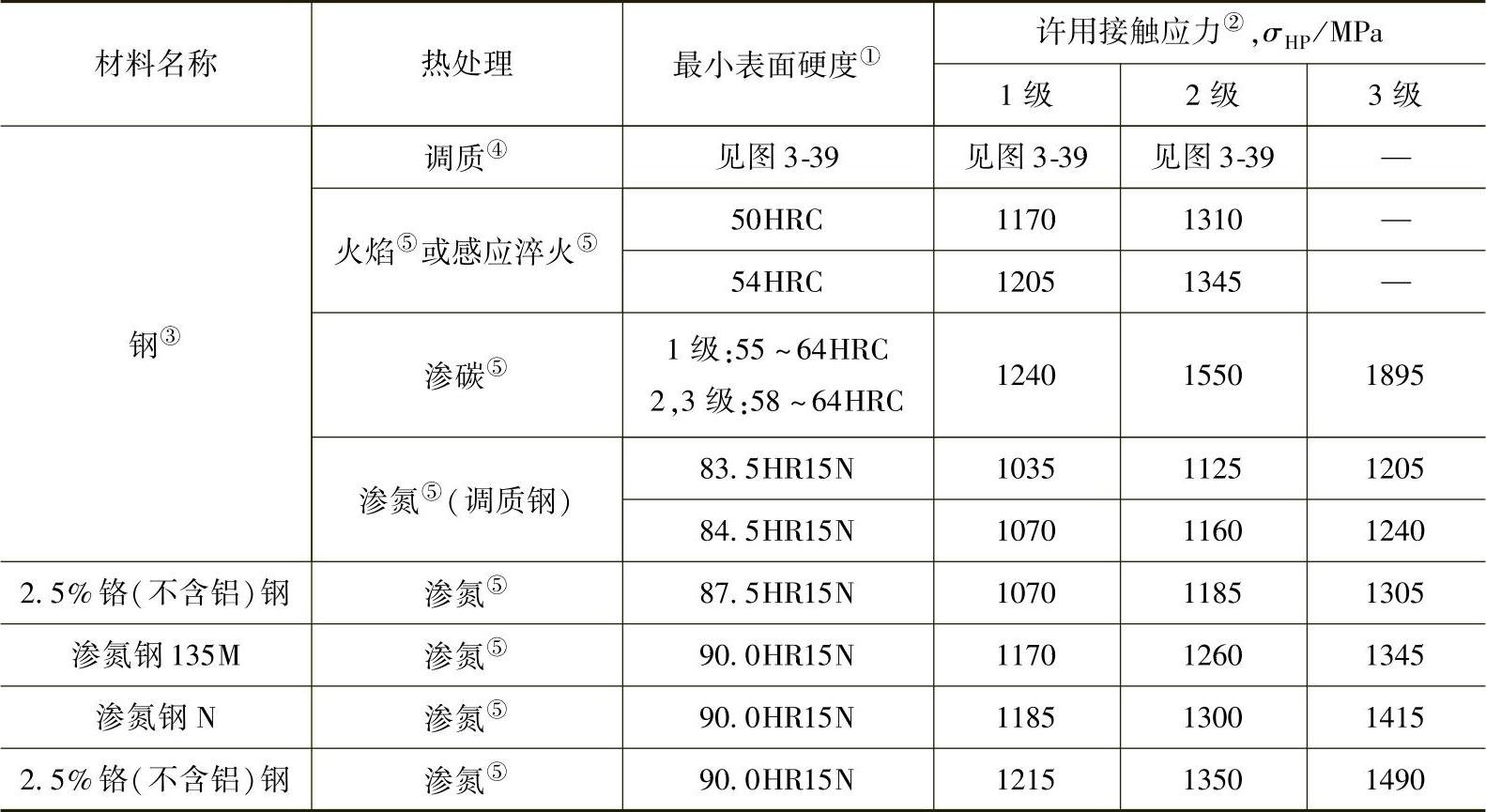
①硬度为齿中部工作齿廓的起始点的硬度。

②参见AGMA923—B05或AGMA2101—D04标准中关于每种应力级别钢的主要冶金要素要求。

③钢的选择必须和热处理工艺及要求的硬度对应。

④这些材料至少要退火或正火。

⑤许用应力的值靠正确的硬化层厚度保证。参见AGMA2101—D04标准推荐的硬化层厚度值。

表3-16 钢齿轮的许用弯曲应力σFP

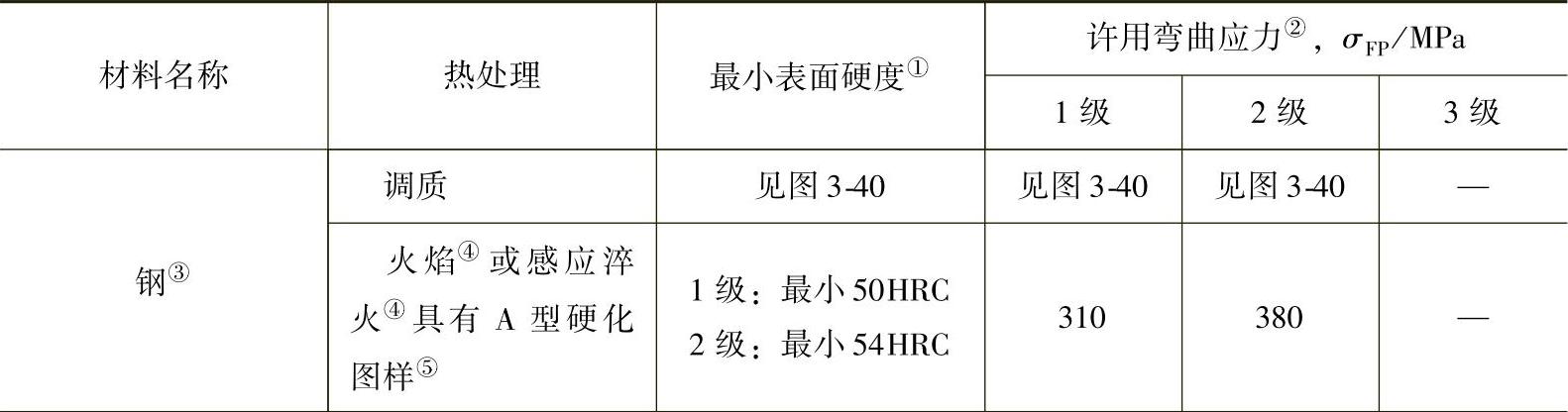
（续）

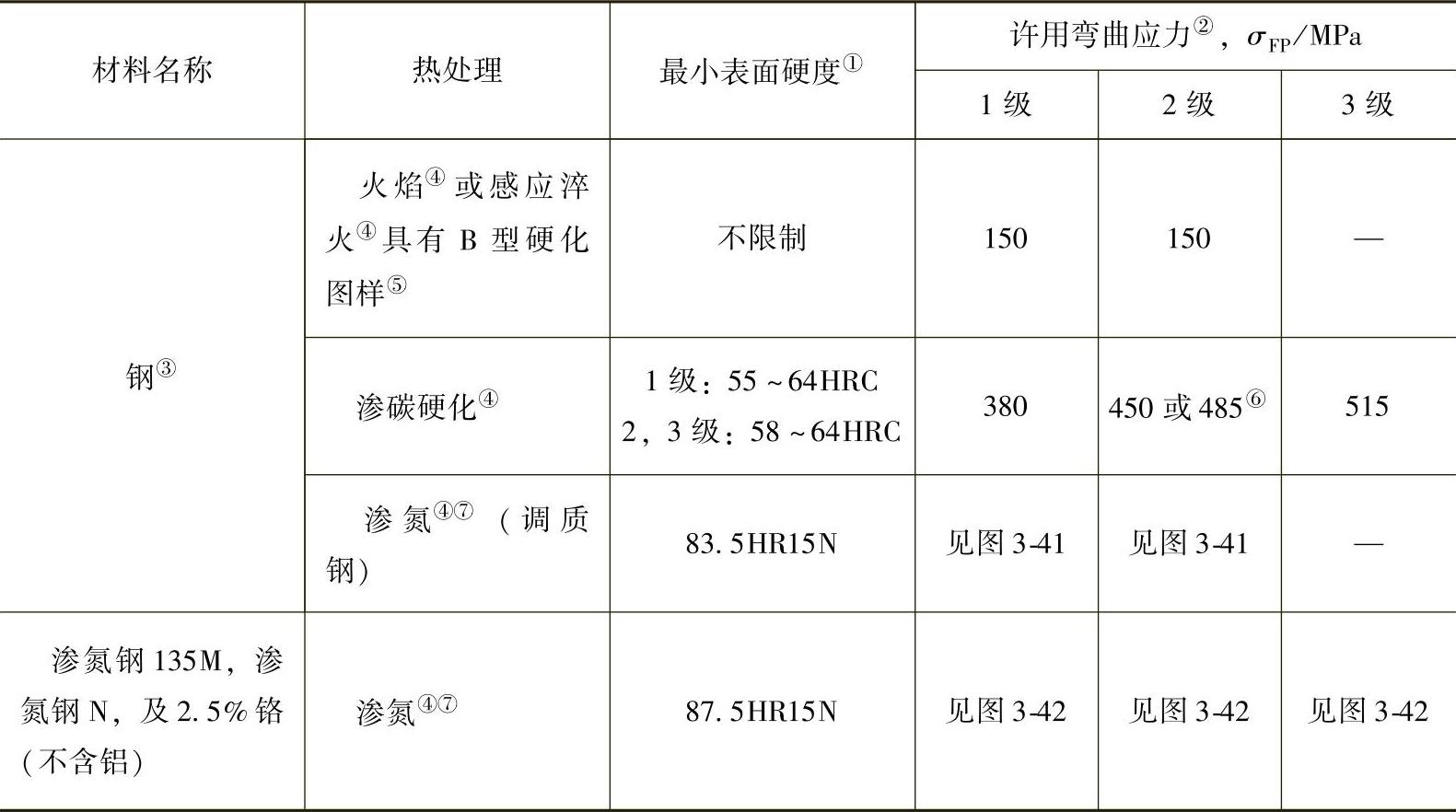
①硬度为齿根圆上齿槽中点的硬度。

②参见AGMA923—B05或AGMA2101—D04标准中关于每种应力级别钢的主要冶金要素要求。

③钢的选择必须和热处理工艺及要求的硬度对应。

④许用应力的值靠正确的硬化层厚度保证，参见AGMA2101—D04标准推荐的硬化层厚度值。

⑤A型硬化图样和B型硬化图样如图3-43所示。

⑥如果贝氏体和微裂纹局限于3级钢，可以取485MPa。

⑦渗氮齿轮的过载能力低。因为有效S-N曲线的形状是平的，在使用设计前应调查其对冲击的敏感性。

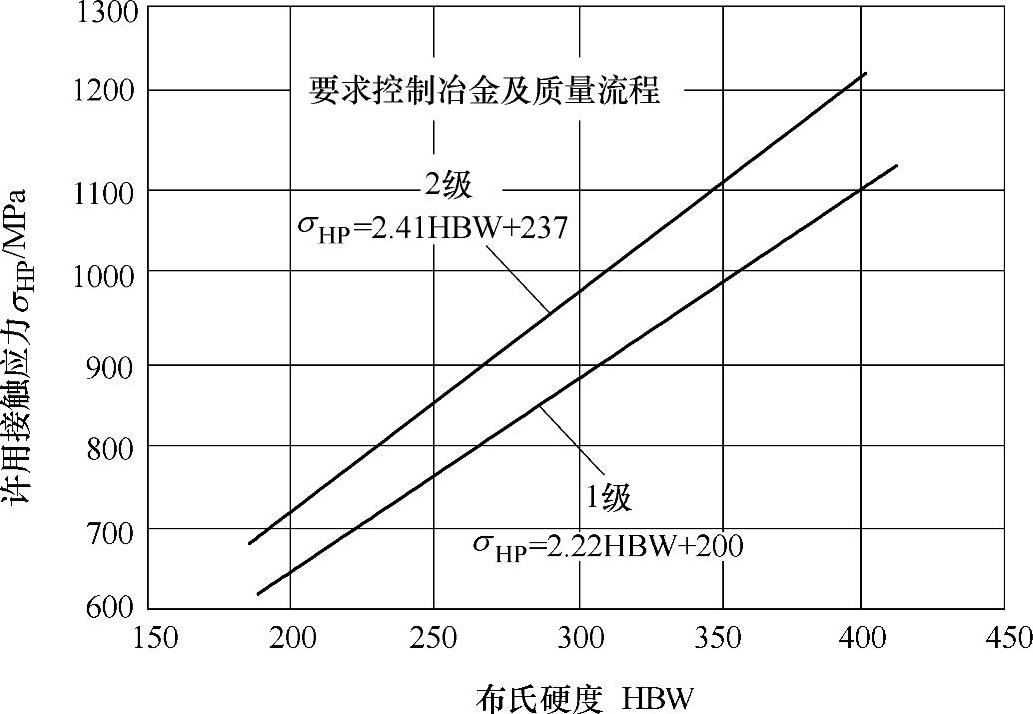
图3-39 调质钢齿轮许用接触应力σ_HP

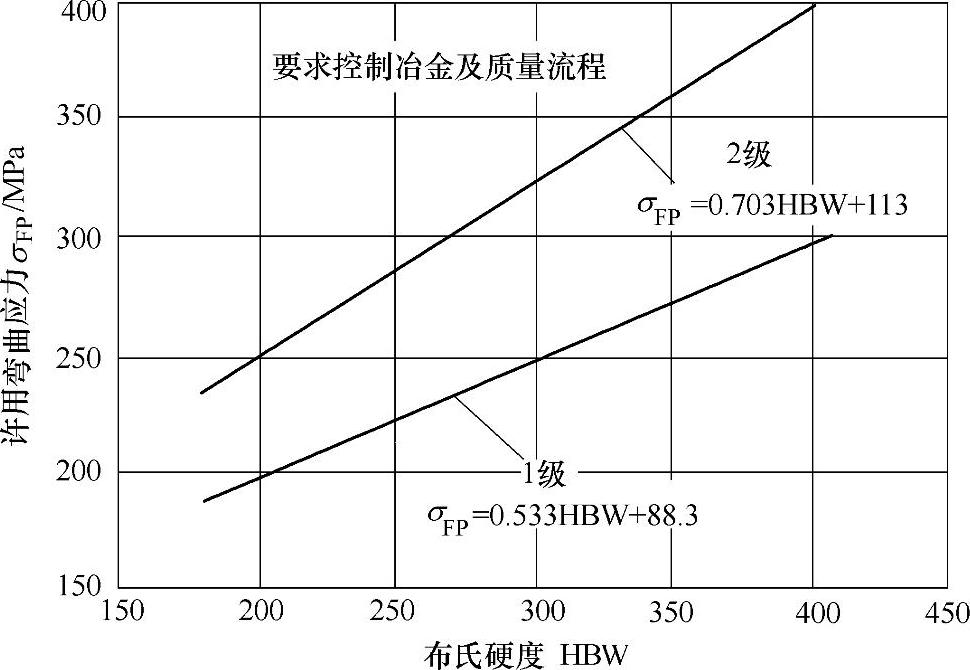
图3-40 调质钢齿轮许用弯曲应力σ_FP

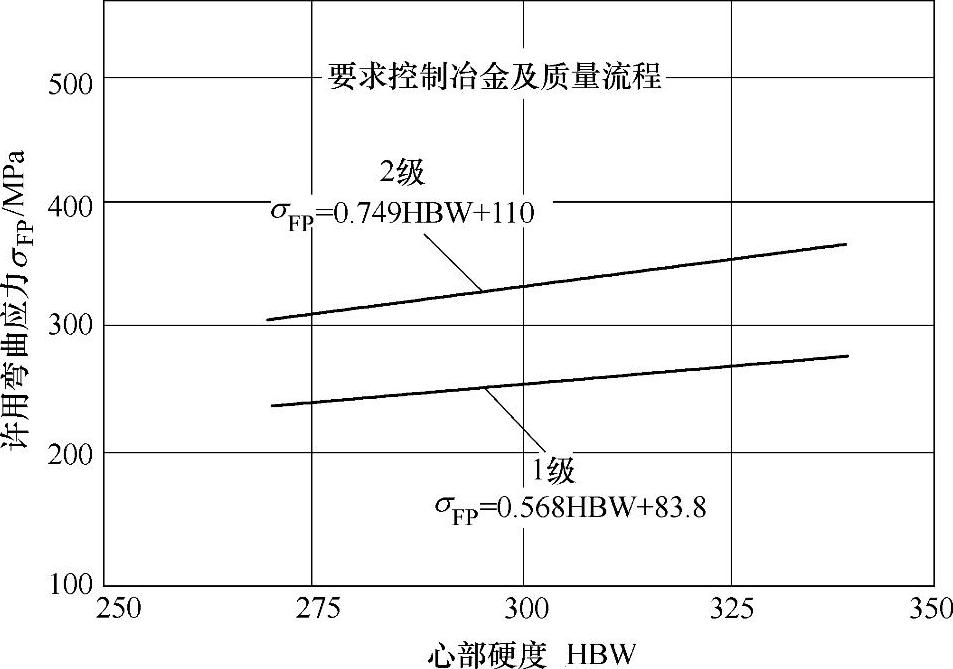
图3-41 渗氮调质钢（如AISI4140、AISI4340）许用弯曲应力σ_FP

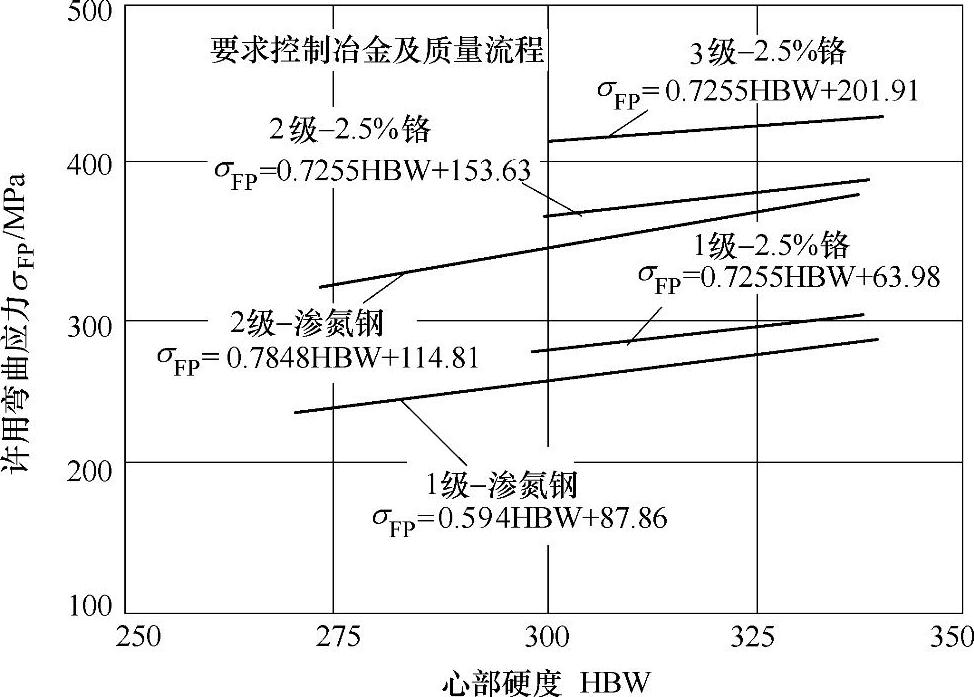
图3-42 渗氮钢齿轮许用弯曲应力σ_FP

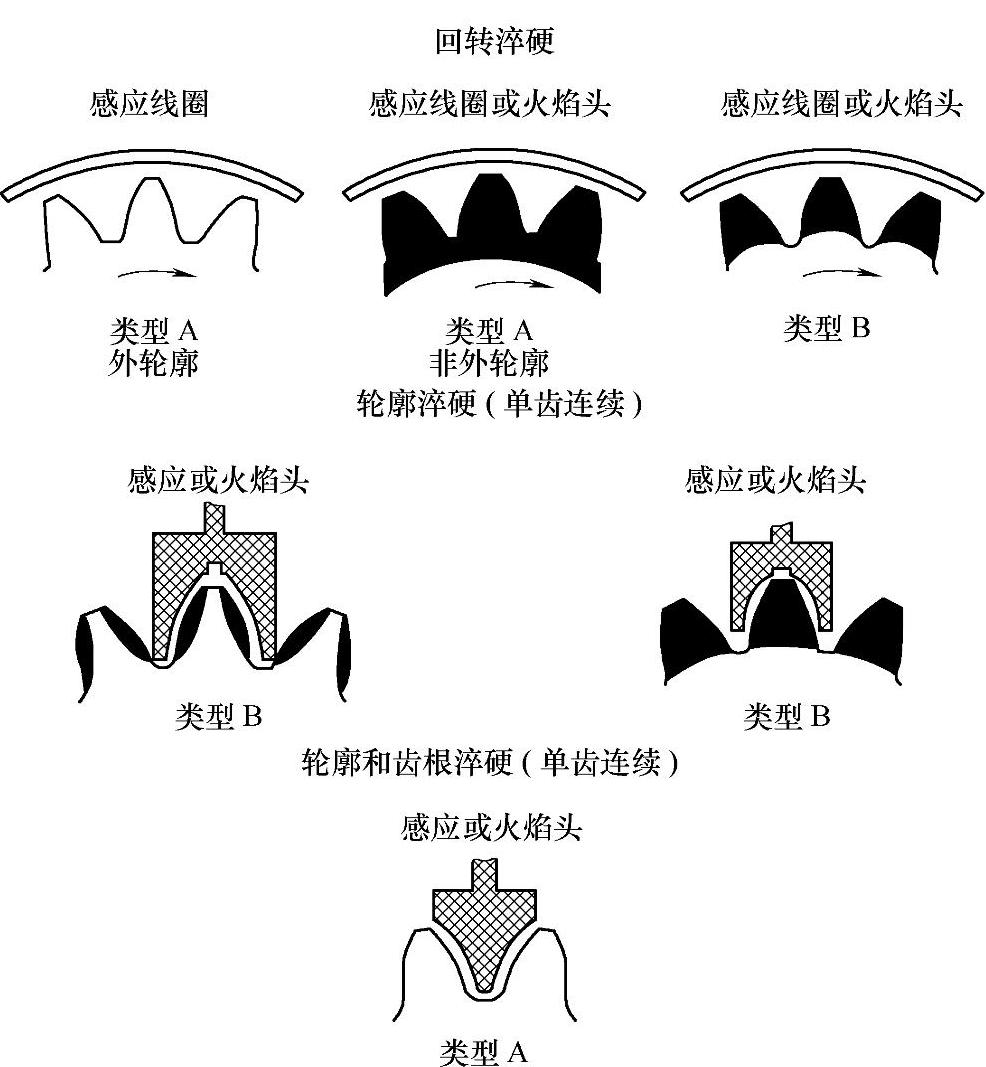
图3-43 通过火焰淬火或感应淬火方法获得的轮齿硬化图样

［注]类型A表示齿廓和齿根都淬硬了，不管是用外齿廓或非外齿轮廓图祥

表3-17 铸铁或铜齿轮的许用接触应力σHP

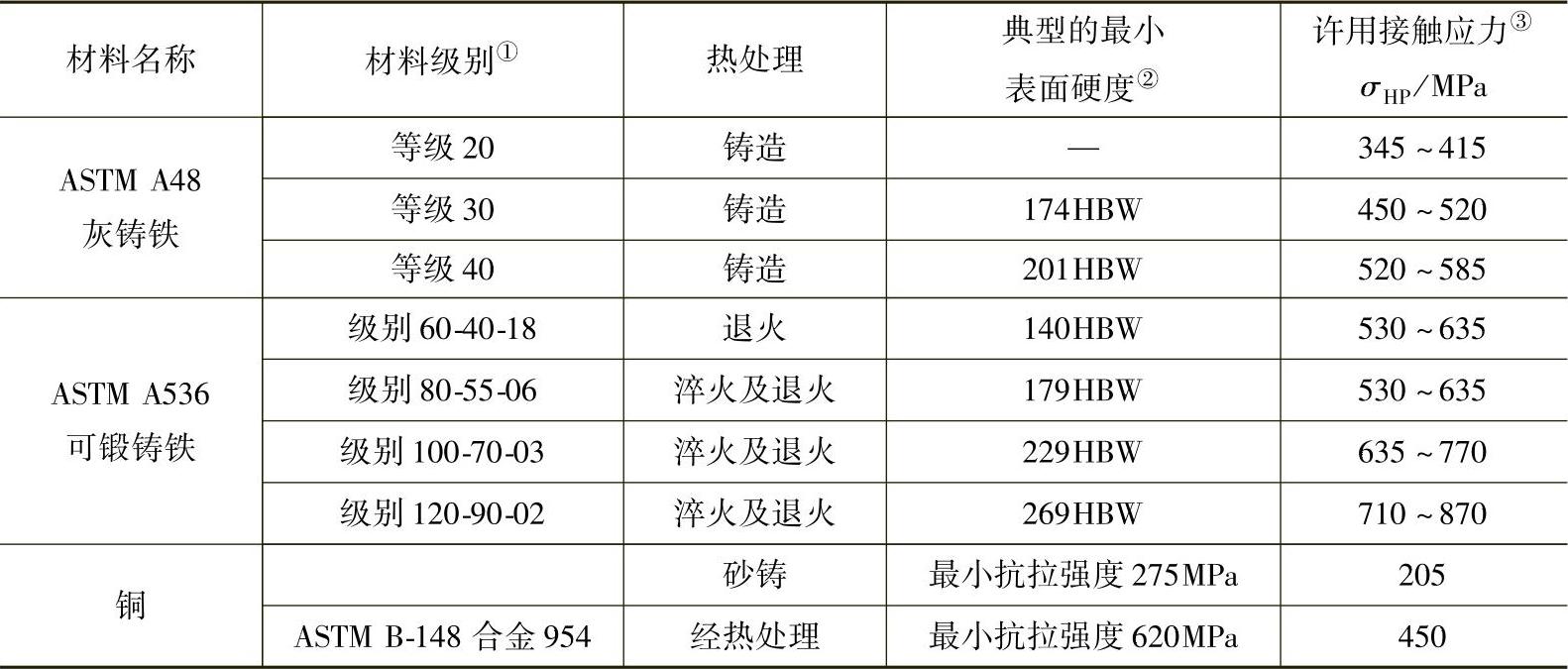
①参见ANSI/AGMA 2004—B89标准：齿轮材料及热处理手册。

②硬度为齿中部工作齿廓的起始点的硬度。

③对一般设计，取下限的值。如果符合下列条件，可以用上限的值：

——使用高质量材料。

——剖面尺寸和设计允许对热处理最大响应。

——通过合适的检验保证质量。

——经现场使用经验验证。

表3-18 铸铁或铜齿轮的许用弯曲应力σFP

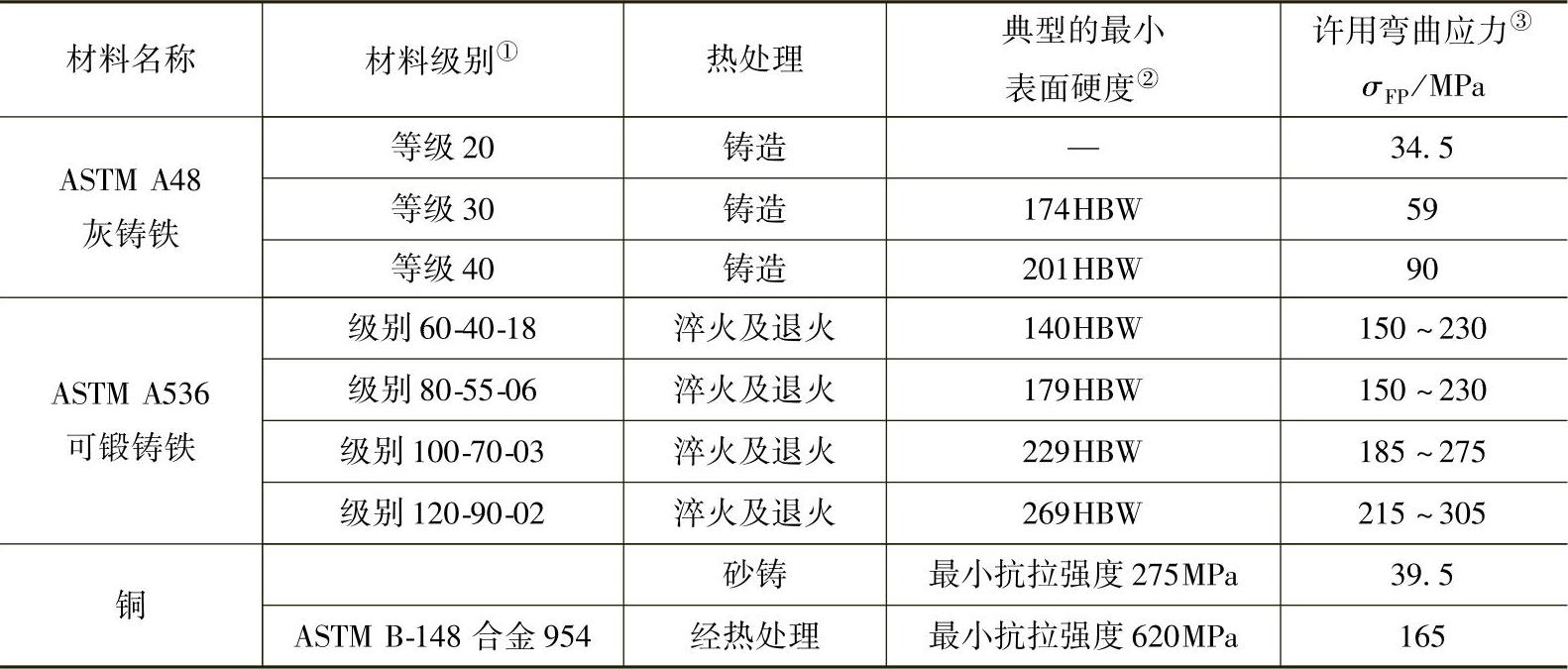
①参见ANSI/AGMA 2004—B89标准：齿轮材料及热处理手册。

②硬度为齿根圆上齿槽中点的硬度。

③对一般设计，取下限的值。如果符合下列条件，可以用上限的值：

——使用高质量材料。

——剖面尺寸和设计允许对热处理最大响应。

——通过合适的检验保证质量。

——经现场使用经验验证。

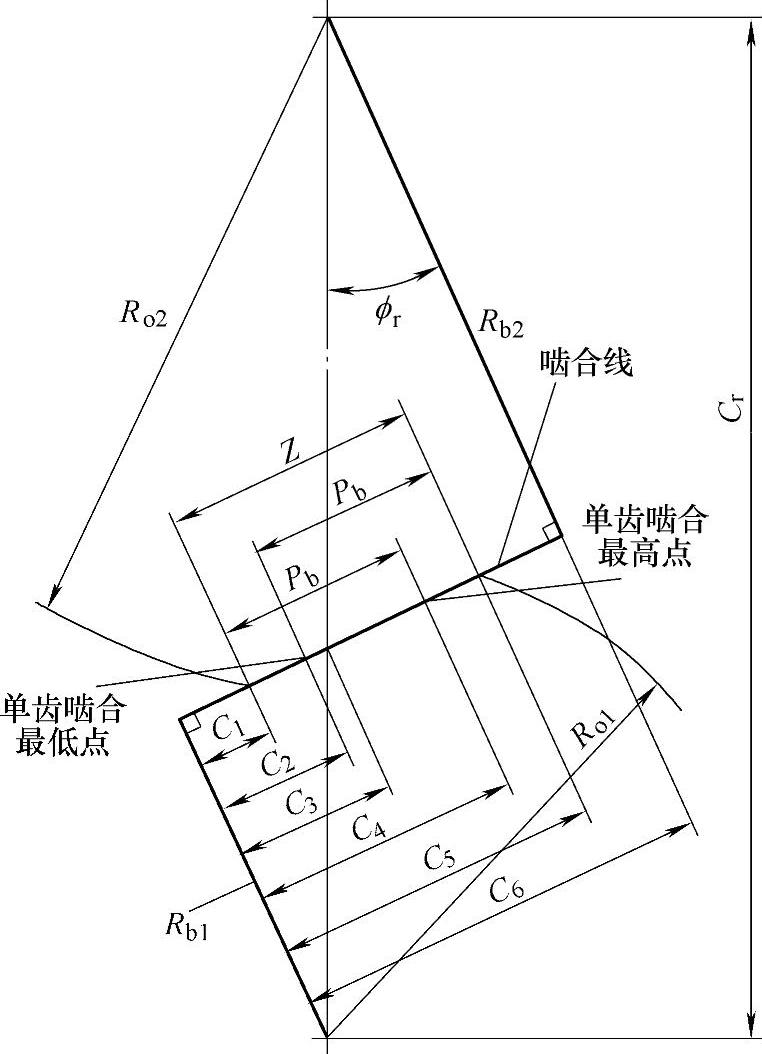
图3-44 啮合线端面图

（10）抗点蚀几何系数ZI

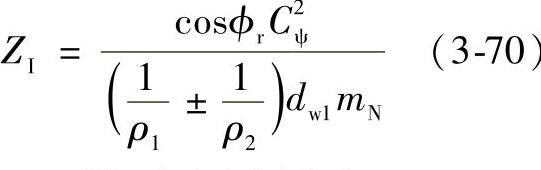
式中 ϕ_r——端面啮合压力角；

C_ψ——斜齿轮重合系数；

m_N——载荷均载系数；

d_w1——小齿轮节圆直径；

ρ₁、ρ₂——小齿轮和大齿轮在接触应

力计算点处的齿廓曲率半径。(www.daowen.com)

参考图3-44，Z_I的计算步骤如下：

第1步，求ϕ_r：

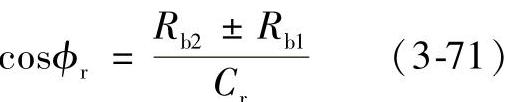
式中 R_b1、R_b2——小齿轮和大齿轮的基圆半径；

C_r——实际中心距。

上面的符号（+）适用于外齿轮传动，下面的符号（-）适用于内齿轮传动；此规定适用于如下其他方程的情况。

第2步，求C₁、C₂、…、C₆及Z：

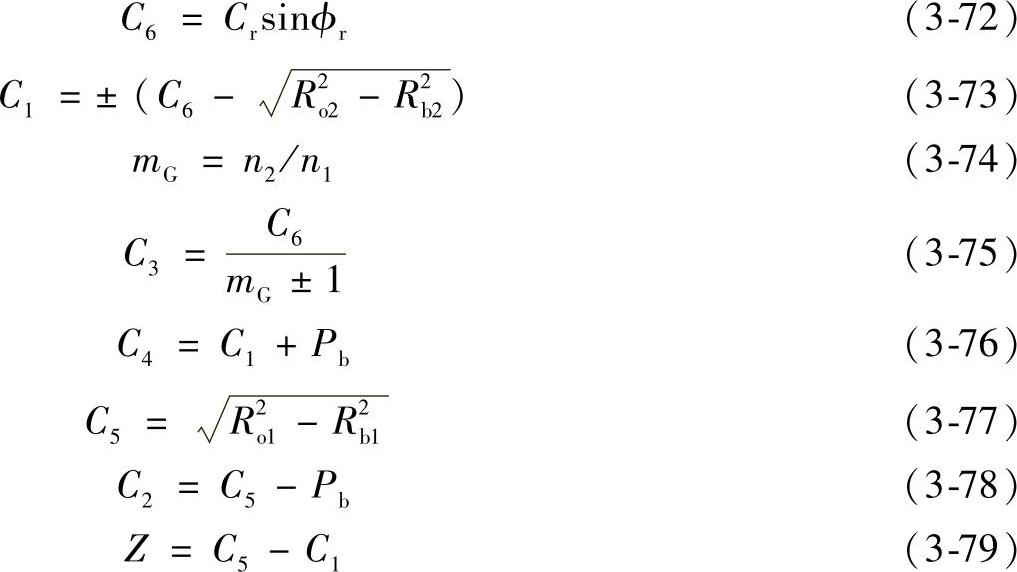
式中 m_G——传动比；

n₁、n₂——小齿轮和大齿轮的齿数；

P_b——端面基圆齿距；

R_o1——小齿轮顶圆半径。

式中 P_N——法面基圆齿距；

m_n——法面模数；

ϕ_n——法面分度圆上的压力角。

第3步，求m_P、m_F、P_x及L_min：

式中 m_P——端面重合度；

m_F——纵向重合度，对于直齿轮，m_F=0；

F——有效齿宽；

P_x——轴向齿距。

对于m_P＜2的直齿轮，

L_min=F（3-85）

对于斜齿轮，存在两种情况。先令n_r和n_a分别为m_P及m_F的小数部分。例如m_P=1.4，则n_r=0.4。

情况Ⅰ：n_a≤1-n_r：

式中 ψ_b——齿廓螺旋线在基圆柱上的螺旋角。

情况Ⅱ：n_a＞1-n_r：

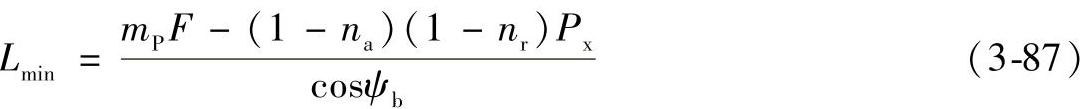
第4步，求m_N：

对于m_F＞1.0的斜齿轮，

m_N=F/L_min（3-88）

对于m_P<2.0的直齿轮或m_F≤1.0的斜齿轮，

m_N=1.0（3-89）

第5步，求ρ₁和ρ₂：

式中

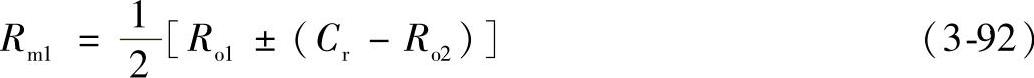
对于直齿轮及m_F≤1.0的斜齿轮，

ρ₁=C₂ （3-93）

ρ₂=C₆∓ρ₁ （3-94）

第6步，求C_ψ：

对于m_F≤1.0的斜齿轮，

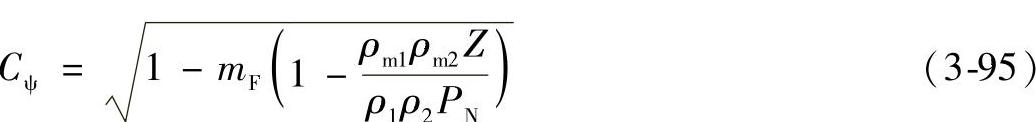
式中

对于直齿轮或m_F＞1.0的斜齿轮，

C_ψ=1.0 （3-98）

第7步，把ϕ_r、C_ψ、ρ₁、ρ₂、d_w1及mN代入式（3-70）求得Z_I。

（11）弯曲强度几何系数，YJ

式中 Y——轮齿形状系数；

C_ψ——斜齿轮重合系数，见式（3-95）或式（3-98）；

K_f——应力校正系数；

m_N——载荷均载系数，见式（3-88）或式（3-89）。

小齿轮和大齿轮的Y_J应分别计算。以小齿轮为例，Y_J的计算步骤如下：

第1步，通过求Z_I，见2.3节（10），而求得m_N和Cψ。

第2步，求虚拟直齿轮副：

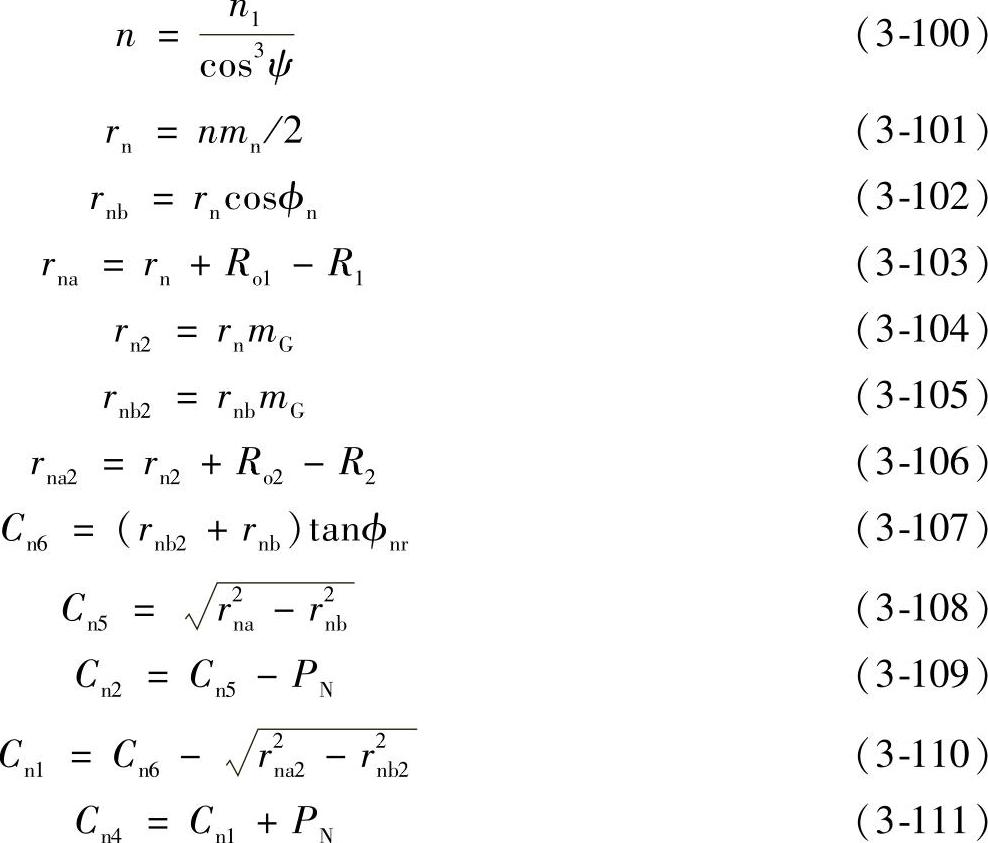
式中 n——虚拟小齿轮的齿数；

r_n、r_n2——虚拟小齿轮和大齿轮的分度圆半径；

r_nb、r_nb2——虚拟小齿轮和大齿轮的基圆半径；

r_na、rna2——虚拟小齿轮和大齿轮的顶圆半径；

ϕ_nr——法面啮合时的压力角；

C_n1、…、C_n6——相对应于图3-44C₁、…、C₆的啮合线参数，不同的是啮合角为ϕ_nr，两个齿轮为虚拟齿轮。

第3步，求ϕ_nW、ϕ_nL及r_nL：

对于斜齿轮（m_F≤1或m_F>1），受载点在齿顶点，这样受载点的压力角见图3-45，可以用如下方程求得：

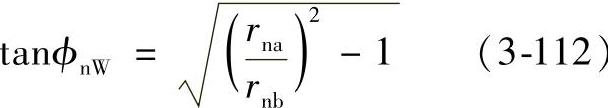
对于直齿轮，如果精度不满足表3-19的要求，受载点也为齿顶点。

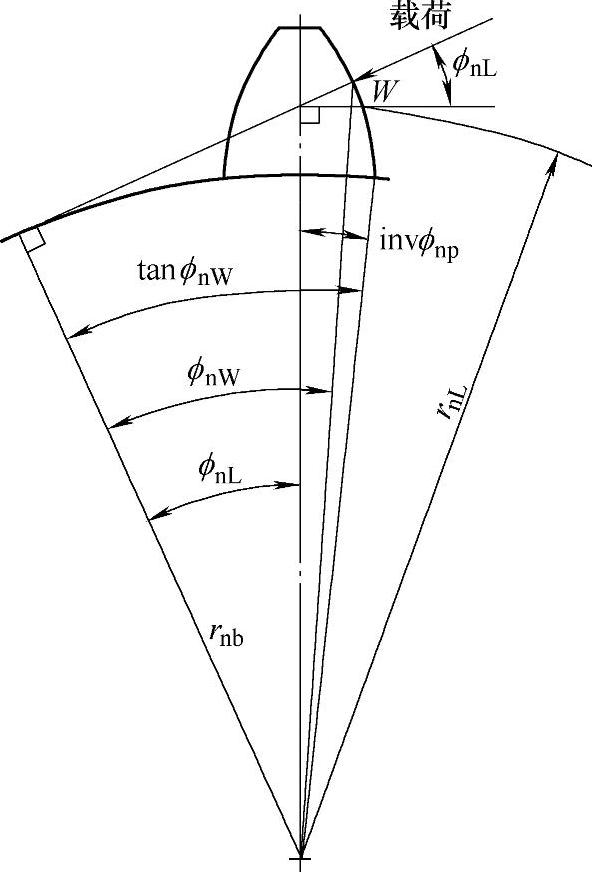
图3-45 载荷角和载荷半径

表3-19 钢直齿轮多齿分担载荷时基节偏差极限

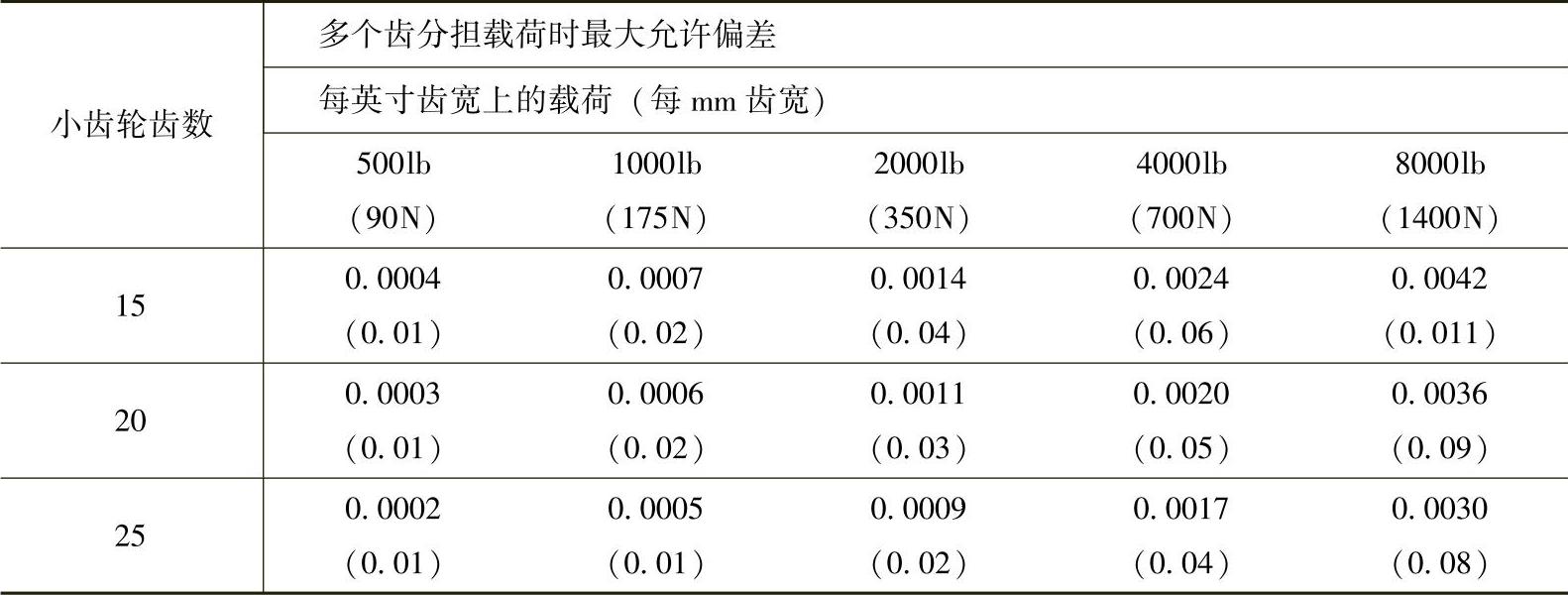
如果直齿轮的精度满足表3-19的要求，受载点为单齿啮合最高点，并且小齿轮的

大齿轮的

对于m_F≤1的斜齿轮，也可以取单齿啮合最高点为受载点，用式（3-113）或式（3-114）求ϕ_nW。

载荷角（单位为弧度）为

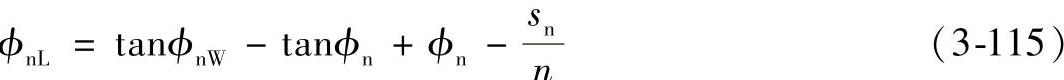
式中 s_n——虚拟齿轮分度圆上的齿厚。

载荷半径

r_nL=r_nb/cosϕ_nL （3-116）

第4步，求虚拟插齿刀及s点的位置

取n_c为真实的插齿刀的齿数。对于使用滚刀加工的齿轮，取n_c=10000。参考图3-46，对应的虚拟插齿刀的参数可以求得如下：

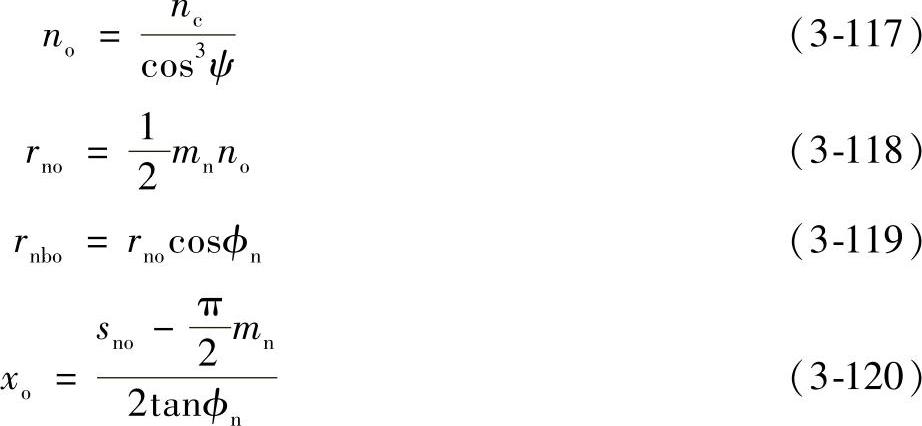
式中 n_o——虚拟插齿刀的齿数；

r_no——虚拟插齿刀分度圆半径；

r_nbo——虚拟插齿刀基圆半径；

s_no——虚拟插齿刀分度圆上法面齿厚；

x_o——虚拟插齿刀的变位系数，对于滚刀，x_o=0。

在刀具圆角半径的中心s：

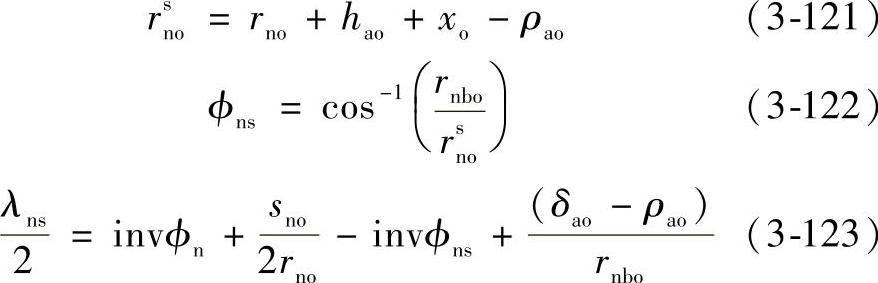
式中 ρ_ao——虚拟刀具的齿顶圆角半径；

δ_ao——磨削余量；

h_ao——虚拟刀具齿顶高度：

h_ao=R_oc^-Rc-xo （3-124）

R_oc——虚拟刀具顶圆半径；

R_c——真实刀具的分度圆半径。

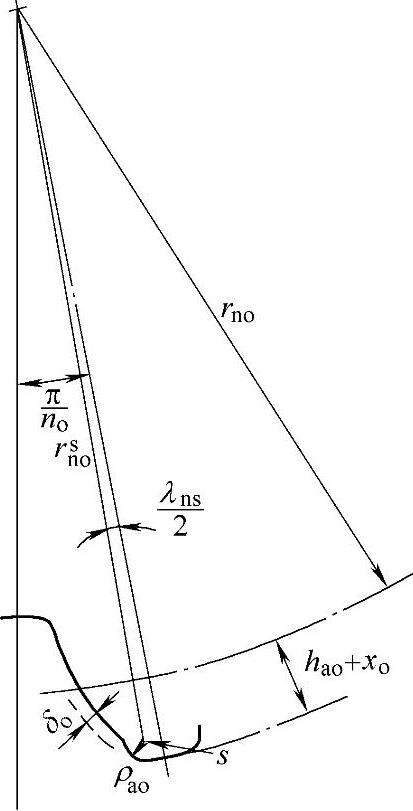
图3-46 虚拟磨削插齿刀

虚拟刀具插齿时的压力角ϕ_n″由下列方程求得：

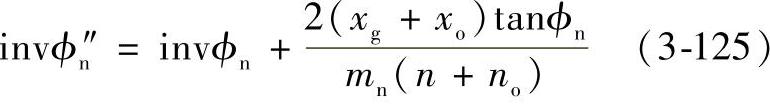
式中 x_g——虚拟直齿轮的变位系数。

插齿时的节圆半径如下：

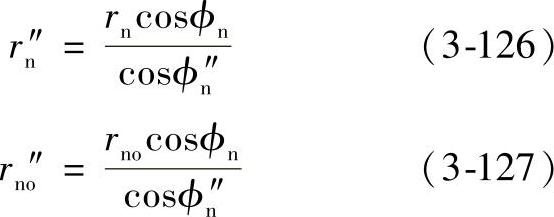
式中 r_n″、r_n″_o——插齿时虚拟齿轮和刀具的节圆半径。

第5步，用迭代法求s_F和h_F

参考图3-47，F是抛物线和齿廓过渡曲线的切点，并且该抛物线的顶点在加载点的法线延伸线上。

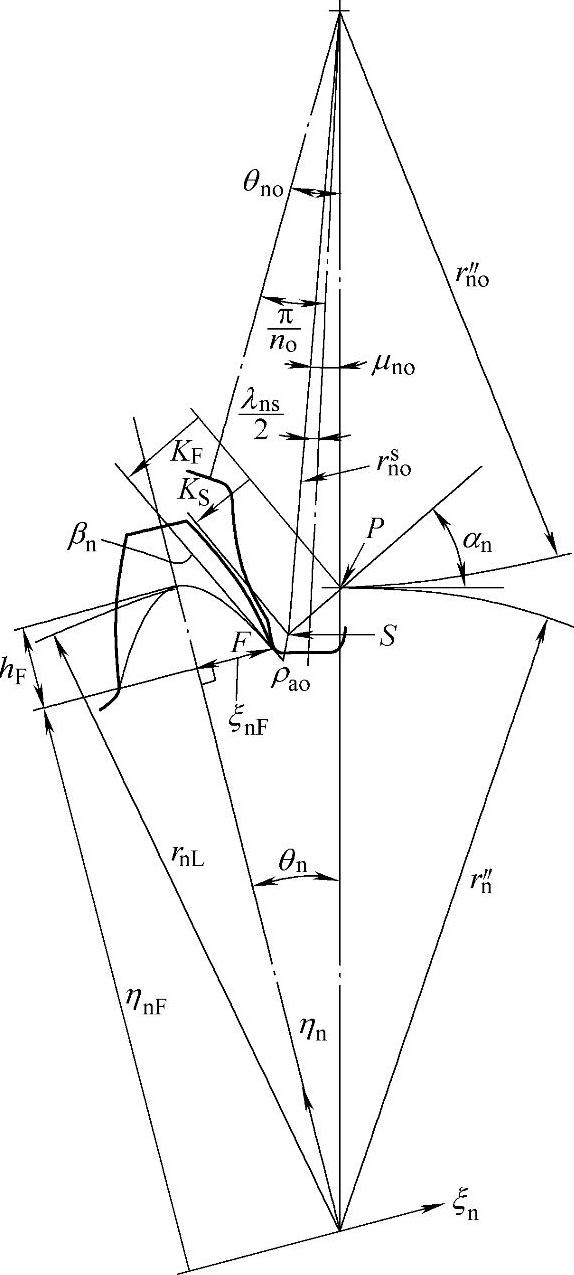
图3-47 虚拟插齿刀和齿轮

初始迭代时，令α_n=π/4，接着进行如下迭代运算：

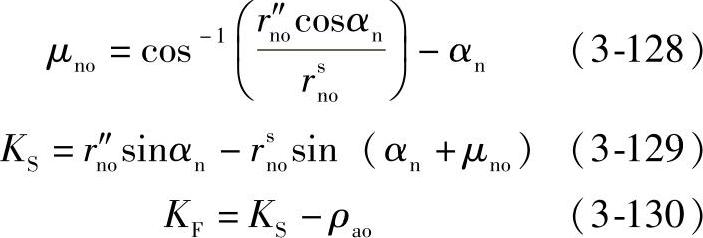
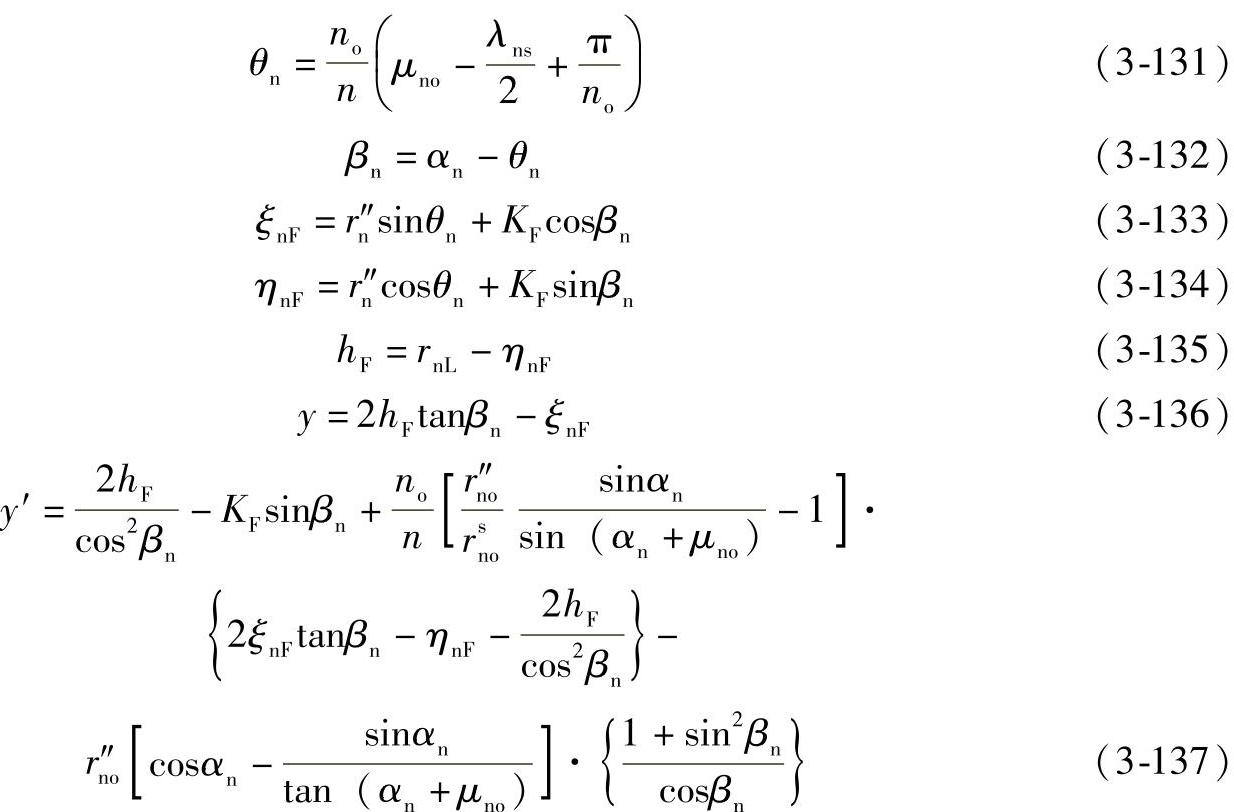
如果|y|的值不接近零，用如下更新的α_n值代入式（3-128）～式（3-137）进行下一步迭代运算：

α_n=α_n（i）-y（i）/y′（i） （3-138）

式中，α_n（i）、y（i）、y′（i）分别为上一次迭代α_n、y、y′的值。最后求得：

s_F=2ξ_nF （3-139）

第6步，求ρ_f：

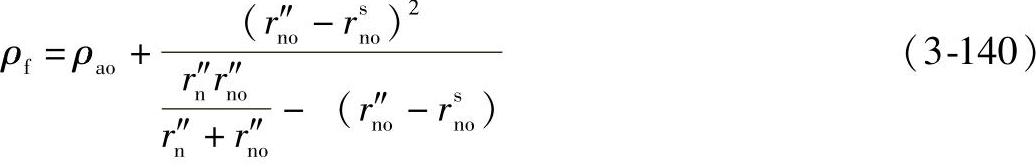
第7步，求C_h：

对于直齿轮和m_F≤1.0的斜齿轮，

C_h=1.0 （3-141）

对于m_F＞1.0的斜齿轮，

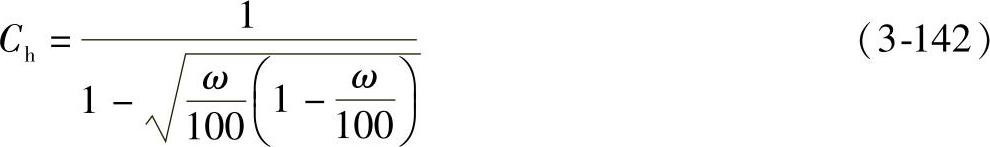
式中

ω=tan-1（tanϕ·sinϕ_n），单位为度。

第8步，求K_f：

式中

H=0.331-0.436ϕ_n （3-144）

L=0.324-0.492ϕ_n （3-145）

M=0.261+0.545ϕ_n （3-146）

且ϕ_n的单位为弧度。

第9步，求螺旋角系数Kψ：

对于直齿轮和m_F≤1.0的斜齿轮，

K_ψ=1.0 （3-147）

对于m_F＞1.0的斜齿轮，

Kψ=cosψ_rcos_ψ （3-148）

式中ϕ_r为节圆柱上的螺旋角。

第10步，求Y：

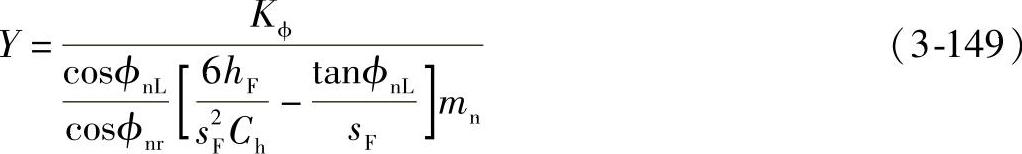
第11步，把Y、K_f、Cϕ及m_N代入式（3-99）求Y_J。