（1）重合度

端面重合度可用公式

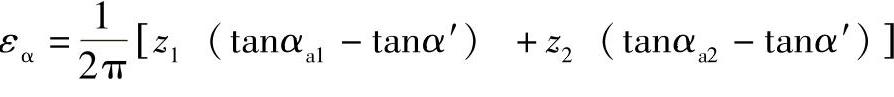
或

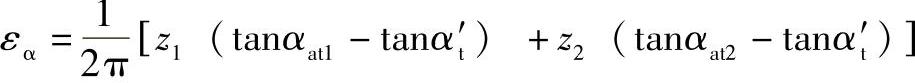
进行计算。

式中 α_a1、α_a2——小、大齿轮顶圆压力角；

α′——啮合角；

α_at1、αat2——小、大斜齿轮顶圆端面压力角；

α′_t——端面啮合角。

也可用图2-24之线图按下式进行计算：

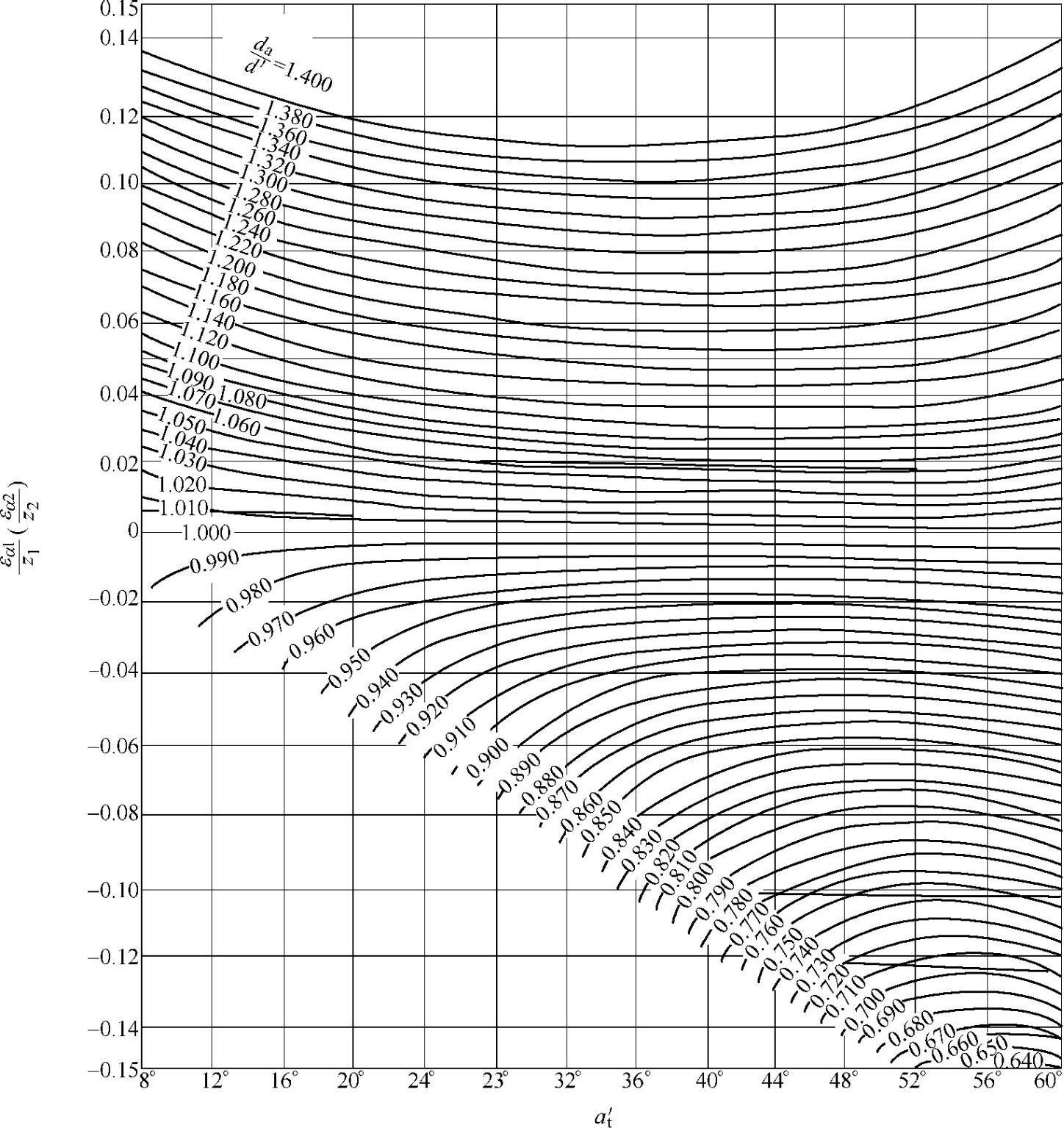
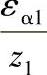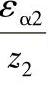图2-24 确定及的线图

式中，ε_α1、ε_α2分别为齿轮1、齿轮2的部分重合度。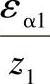、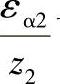可分别按α_t′、d_a1/d′₁及d_a2/d₂′由图2-24确定。其中端面啮合角α_t′可按β及（x₂±x₁）/（z₂-z₁）由图2-25查得（标±号者，正号用于外啮合，负号用于内啮合）。

纵向重合度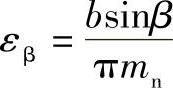，对于直齿轮传动ε_β=0，也可用图2-26之线图确定。其中，b为齿宽（mm）；β为螺旋角；m_n为法向模数。

总重合度ε_γ=ε_α+ε_β（2-32）

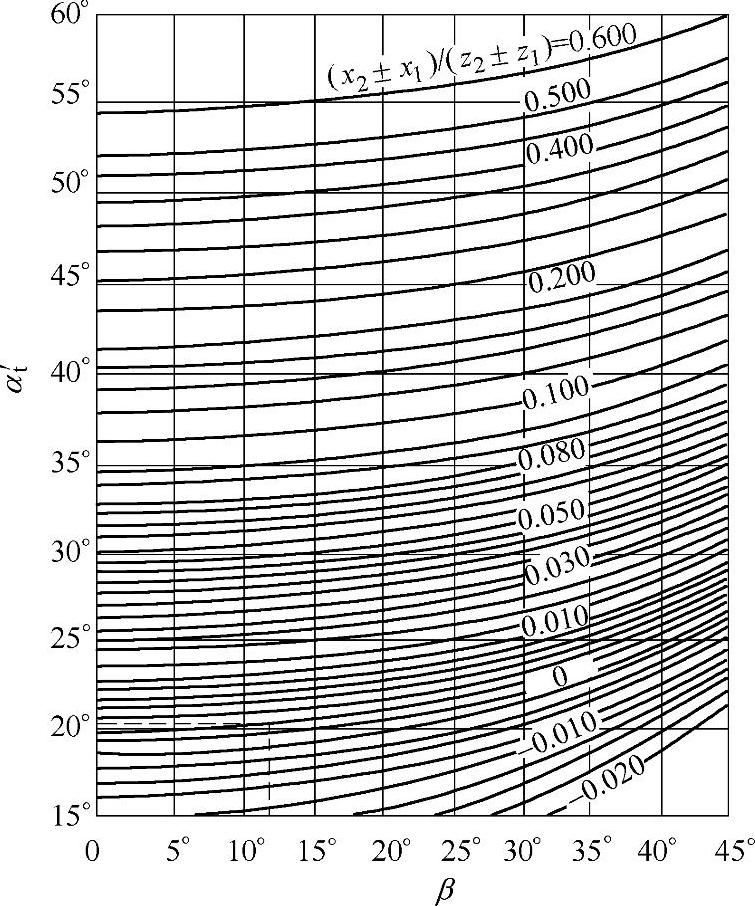
图2-25 端面啮合角α_t′

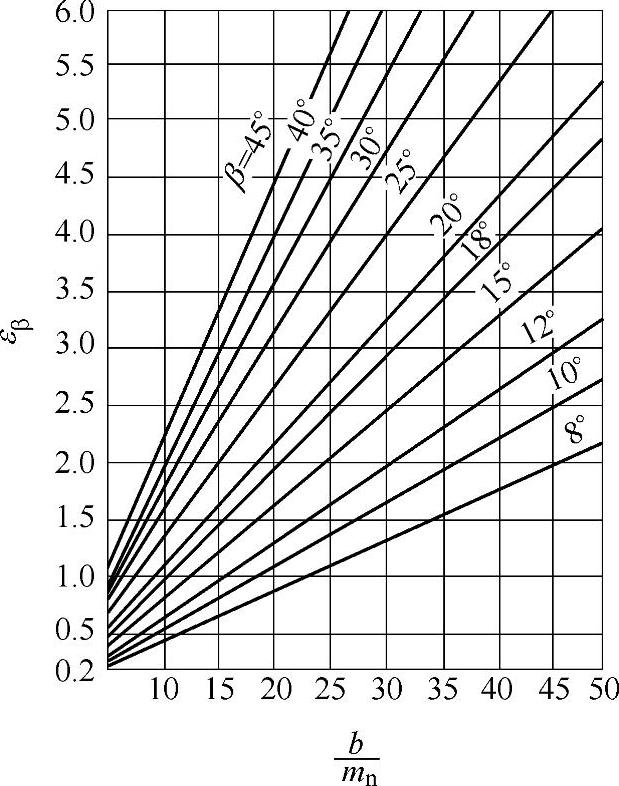
图2-26 纵向重合度εβ

【例2-9】 一对外啮合斜齿圆柱齿轮，z₁=21，z₂=74，m_n=3mm，β=12°，x_n1=0.5，x_n2=-0.5。根据计算，d′₁=64.408mm，d₂′=226.960mm，d_a1=73.408mm，d_a2=229.960mm。试确定端面重合度ε_α。

解 按β=12°，（x₂+x₁）/（z₂+z₁）=0，由图2-25查得α′_t=20°25′。

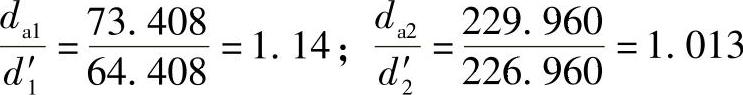
按α_t′、d_a1/d′₁、d_a2/d₂′，由图2-24查得=0.051，εα2=0.006。

z₁z2

故

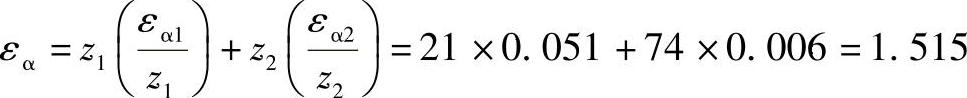
纵向重合度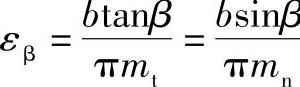，也可按图2-26之线图确定。

表2-38 标准直齿圆柱齿轮传动的重合度

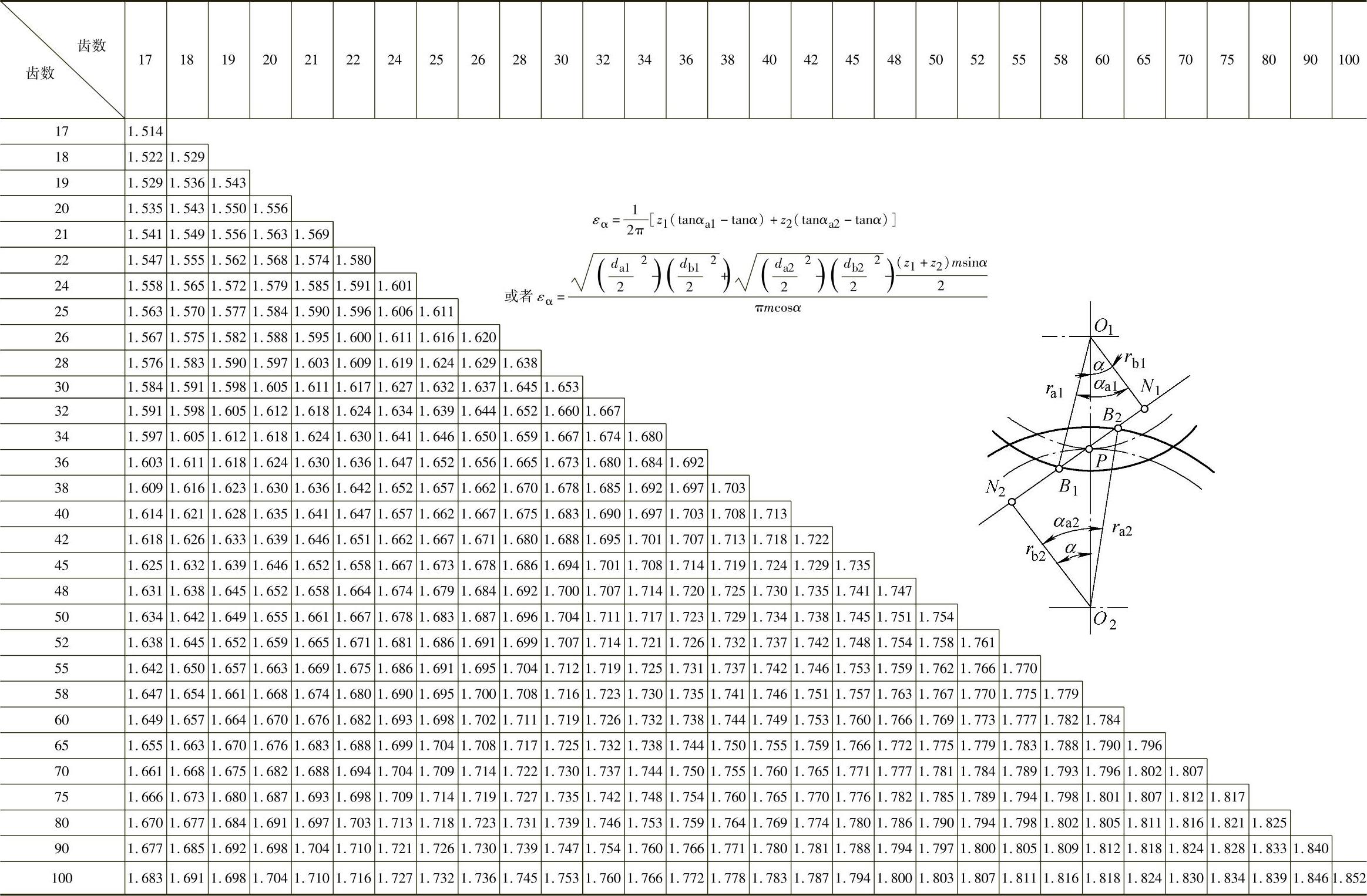
总重合度ε_γ=ε_α+ε_β

对于正常齿的标准直齿轮传动，重合度ε_α（因为ε_β=0）总是小于2，其不同齿数组合的传动重合度ε_α见表2-38。

对于一对外啮合直齿轮传动，若两轮的齿数不断增多，其重合度不断增大，假若两齿轮的齿数趋于无穷多时，其重合度趋于一个极限值ε_max，此时相当于两个齿条啮合，所以

对于不同的分度圆压力角α和齿顶高系数h_a*，其啮合角α′大于或等于分度圆压力角α时，ε_max值见表2-39。

表2-39 ε_max值

上述表明ε_γ值越大，则齿轮传动的连续性越好，传动越平稳；但ε_γ值不可能无限地增大，通常以接近2为好。一般设计时，要求ε_γ≥[ε_γ]，许用[ε_γ]值见表2-40。

表2-40 推荐重合度的许用值[ε_γ]

（2）滑动率

表示齿面间相对滑动的程度。就是在轮齿接触点处，两齿面间相对切向速度（即滑动速度）与该点切向速度的比值，用η表示。

1）外啮合齿轮传动滑动率的计算（见图2-27～图2-29）

小齿轮齿面的滑动率

大齿轮齿面的滑动率

式中 u=z₂/z₁——齿数比。

小齿轮齿根处的最大滑动率

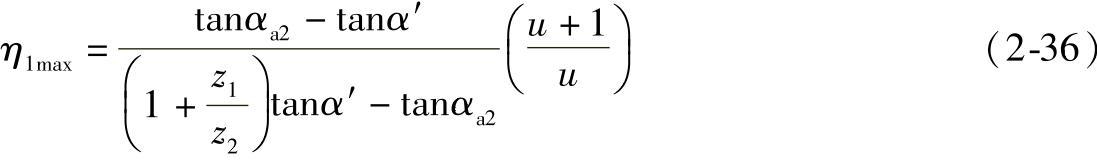
大齿轮齿根处的最大滑动率

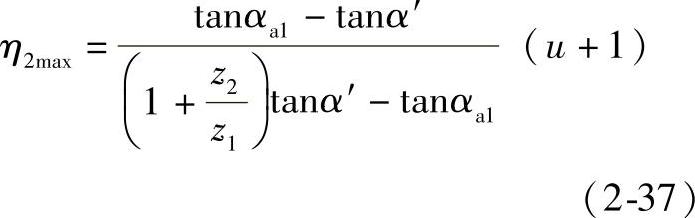
2）内啮合齿轮传动滑动率的计算（见图2-30）

外齿轮齿面的滑动率

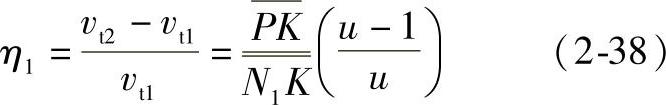
内齿轮齿面的滑动率(www.daowen.com)

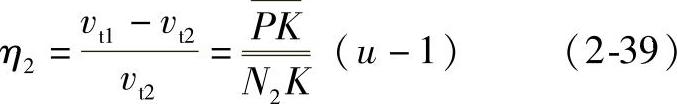
外齿轮齿根处的最大滑动率

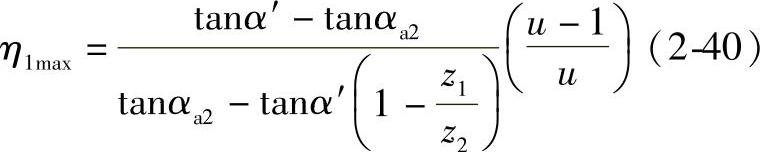
内齿轮齿根处的最大滑动率

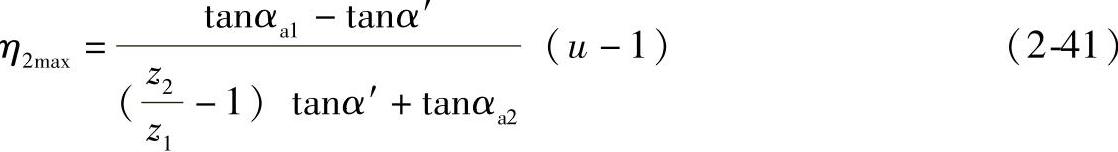
从上述公式中可以看出：滑动率η是啮合点位置的函数，其值在0～∞之间变化；轮齿在节点p啮合时，η₁=η₂=0，在节点两侧的不同点啮合时，由于滑动速度方向的改变而使滑动率符号改变；轮齿若在极限点N₁或N₂啮合时，η₁或η₂将分别达到∞，造成轮齿的严重磨损，故应避免轮齿在极限点啮合；实际上，轮齿只能在实际啮合线B₁B₂上啮合。在B₂点啮合时，齿轮1齿根的滑动率η₁达到实际的最大值η_1max。在B₁点啮合时，齿轮2齿根的滑动率达到实际的最大值η_2max。

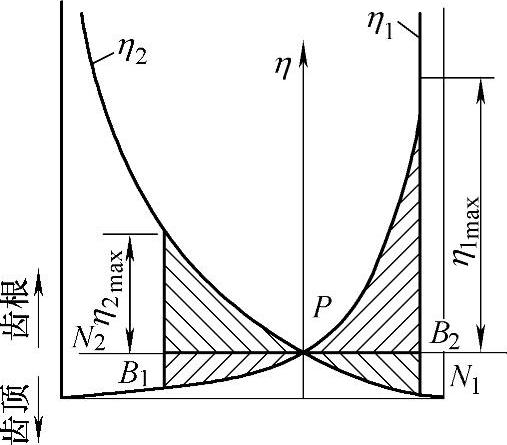
图2-28 外啮合齿轮滑动率曲线

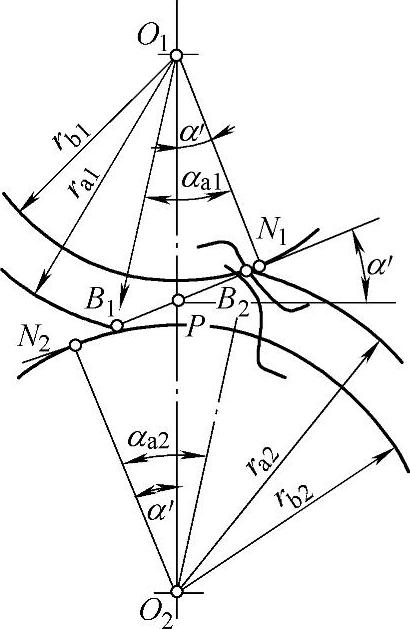
图2-29 最大滑动率的计算图

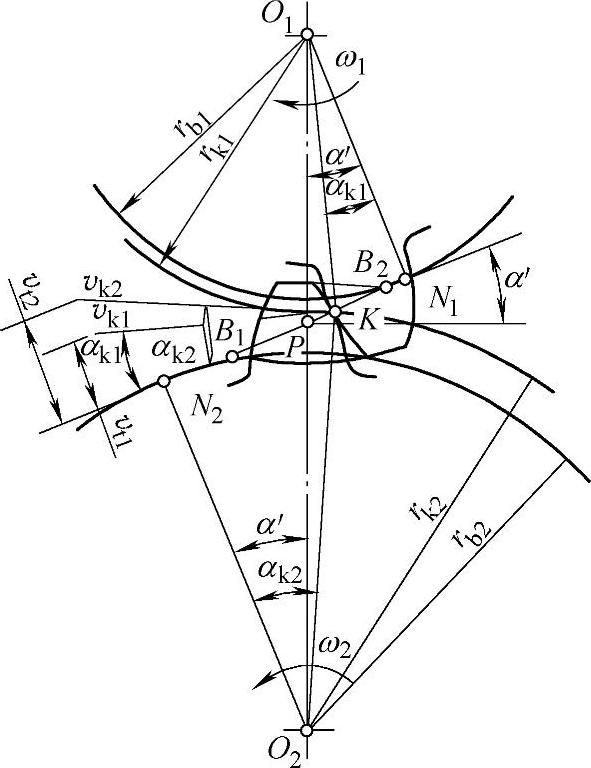
图2-27 滑动率的计算图

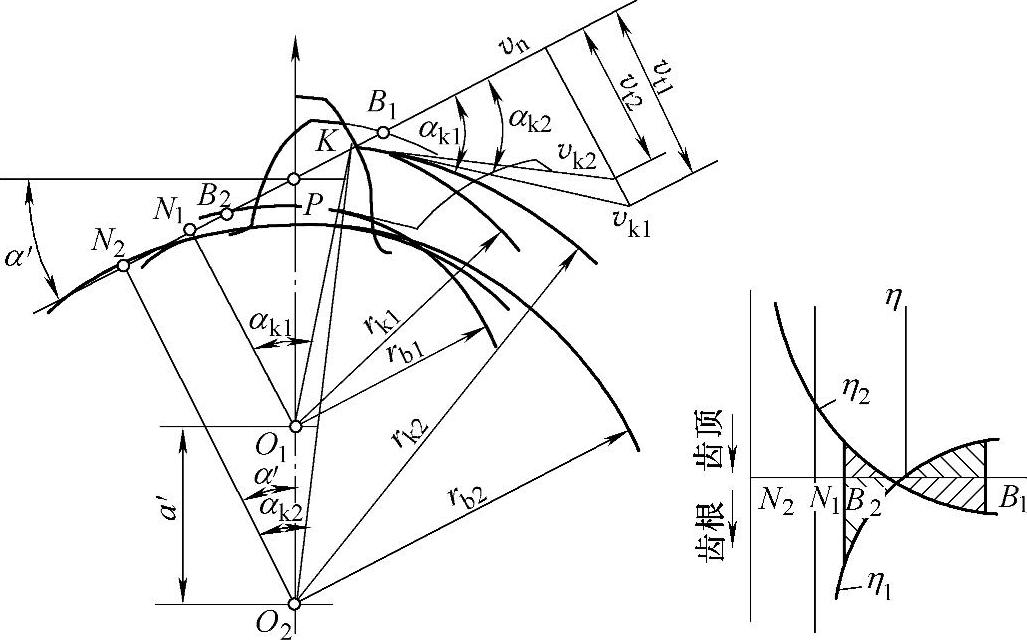
图2-30 内啮合齿轮传动的滑动率

还应指出，在相同的工作时间内，大、小齿轮参与啮合的次数是不同的，大齿轮2的齿廓参与啮合的次数仅为小齿轮1的齿廓参与啮合次数的1/u倍，所以，在连续工作过程中，大齿轮齿廓的磨损系数应为其滑动率的1/u倍。

滑动率的大小不仅影响到齿轮齿面的磨损，而且还影响到齿面的胶合损坏，因此，为提高齿轮的抗胶合和耐磨损能力，应尽量减小滑动率η的数值。

经验表明，齿轮齿廓的滑动率不应大于下表2-41数值：

表2-41 滑动率

（3）渐开线齿廓的几何压力系数

渐开线齿廓间的正压力不仅影响齿廓的磨损，而且由于正压力所产生的接触应力还直接影响齿廓表面的点蚀损坏。因此，必须研究齿廓啮合过程中，齿面接触应力的变化。齿面接触区的最大应力，可根据赫兹公式确定：

式中 F_n——接触点处的正压力（N）；

E——当量弹性模量（MPa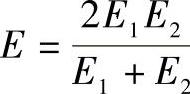），，E1、E2分别为两齿轮材料的弹性模量；

b——齿宽（mm）；

ρ——当量曲率半径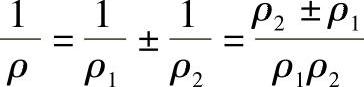，，ρ₁、ρ₂分别为接触点处两齿廓的曲率半径（mm）；式中“+”号用于两个凸曲面接触（即外啮合齿轮传动），“-”号用于凸曲面与凹曲面接触（内啮合齿轮传动）。

对于外啮合齿轮：ρ₂+ρ₁=a′sinα′（见图2-31）

对于内啮合齿轮：ρ₂-ρ₁=a′sinα′（见图2-30）

式中，a′为中心距；α′为啮合角。

于是得

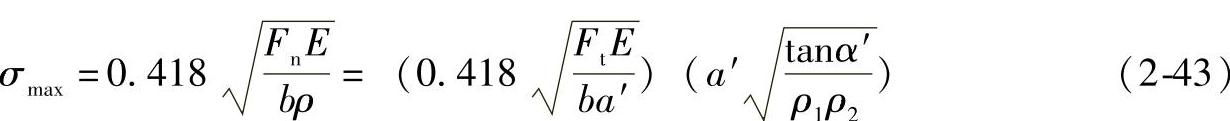
式中 F_t=F_ncosα′。

式（2-43）中第一个括号内的数值因次与应力σ_max的因次相同，它与载荷F_t及齿轮材料的弹性模量E有关；第二个括号中的数值为无因次的系数，它与齿廓的几何形状及接触点的位置有关，因而称为几何压力系数，以ψ表示，即

当齿轮传动的其他条件一定时，几何压力系数ψ越大，轮齿上的接触应力σ_max就越大，齿面的接触强度就越低。

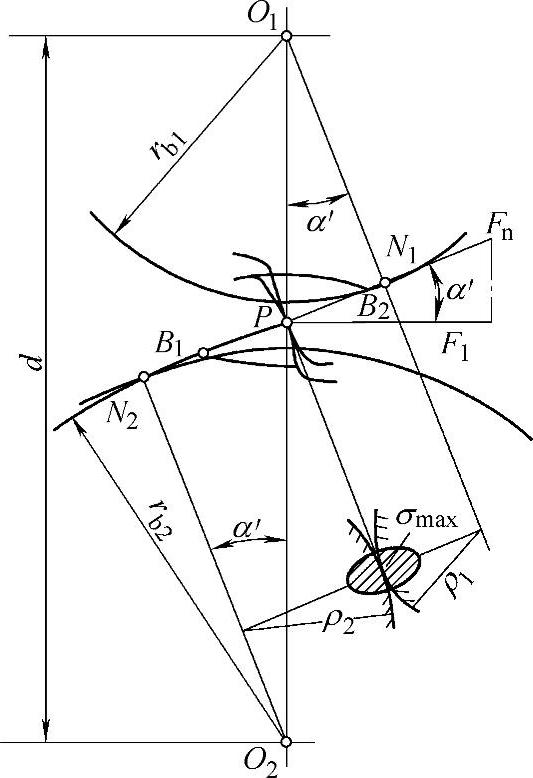
图2-31 齿廓曲率半径及接触应力

从公式（2-44）知，当齿轮的中心距a′及啮合角α′一定时，几何压力系数ψ与曲率半径ρ₁ρ₂有关，即ψ仅为啮合点位置的函数。于是：

1）当轮齿在极限点N₁（或N₂）啮合时，曲率半径ρ₁（或ρ₂）将为0，此时的ψ=∞，齿廓间的最大接触应力在理论上将达∞。从这一点考虑，应避免轮齿在极限点N₁（或N₂）处啮合。

2）对于外啮合齿轮，当轮齿在理论啮合线N₁N₂中点啮合时，由于ρ₁+ρ₂=a′sinα′，故此时ρ₁=ρ₂=1/2a′sinα′，其乘积ρ₁ρ₂将达最大值，因而此时的几何压力系数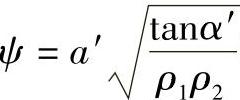将达到最小值：

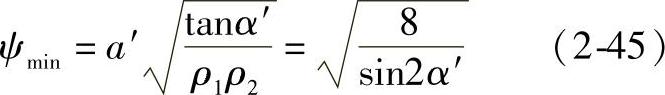
只要给定啮合角α′，即可求得ψ_min。

节点p处的几何压力系数ψ_p为

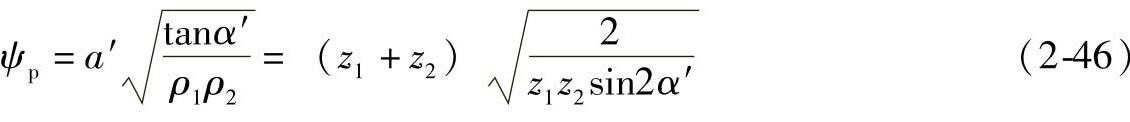
上式表明sin2α′越大，ψ_p越小，齿面承载能力越高，且与sin2α′成正比。因此，变位齿轮齿面承载能力比标准齿轮齿面承载能力提高的程度，可用比值ψ表示：

当其他条件一定时，啮合角α′越大，齿轮齿面承载能力就越高，即几何压力系数就越小。

几何压力系数曲线：当齿轮传动的中心距a′和啮合角α′一定的情况下，轮齿在不同点啮合时，可求得不同的ψ值，对于外啮合传动，可绘出图2-32的ψ曲线；对于内啮合传动可绘出图2-33的ψ曲线。

上述曲线系在重合度ε=1时的情况，但在实际啮合的齿轮，其重合度ε＞1，在实际啮合线的两端点B₁、B₂处均有两对齿分担载荷，因而其实际接触应力却较小，而在节点p附近，只有一对轮齿啮合，因而实际接触应力反而较大，这种情况下，外啮合齿轮传动的实际几何压力系数如图2-34所示。

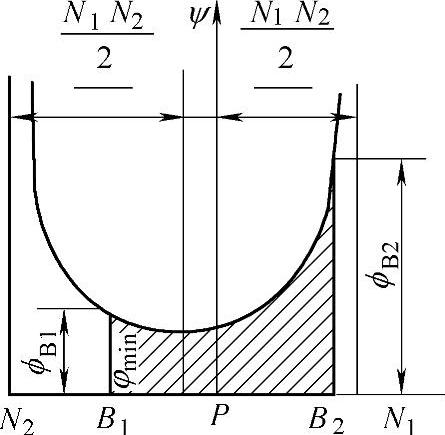
图2-32 外啮合齿轮传动的几何压力系数

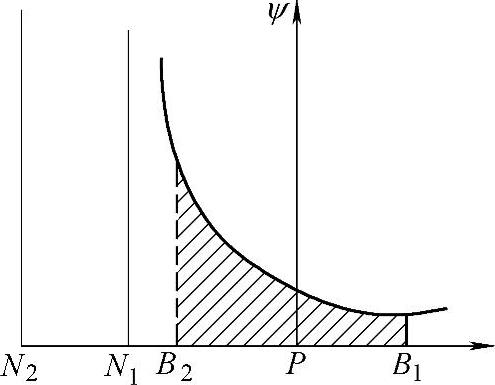
图2-33 内啮合齿轮传动的几何压力系数

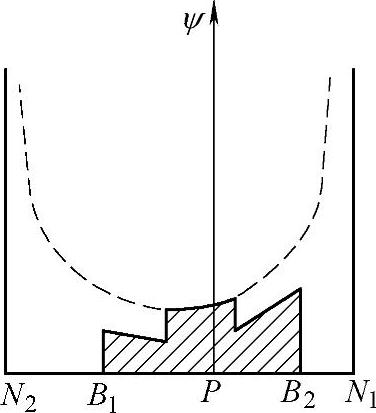
图2-34 外啮合齿轮传动的实际几何压力系数

实际表明，外啮合齿轮传动的点蚀破坏都发生在节点附近的齿根处。因此，为了提高齿轮的承载能力，就必须设法降低节点附近的几何压力系数。