为了说明线图的由来和具体应用，现将变位齿轮传动的一些基本公式作一简述：中心距变动系数y_t：

式中 a′——变位齿轮传动的中心距；

a——标准中心距；

m_t——端面模数，对于直齿轮m_t=m；

m_n——法向模数。

端面啮合角α′_t为

式中 α_t——端面压力角，对于直齿轮α_t=α。由式（2-14）、式（2-15）得中心距变动系数y_t为

式中 z_∑=z₂±z₁——齿数和，“+”号用于外啮合，“-”号用于内啮合。当螺旋角β=0时，则

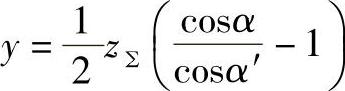
式中 α′——直齿轮传动啮合角。

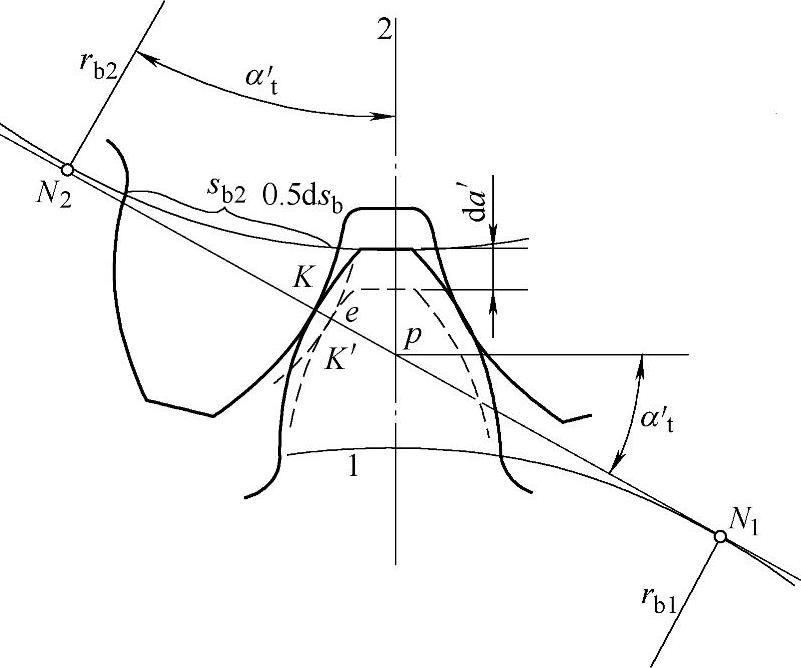
图2-10 x_∑、z_∑和α_t′相互关系公式的推导

图2-10所示为小齿轮1和大齿轮2的轮齿作无侧隙啮合的情况。当中心距增大da′值后，便产生侧隙，其大小为

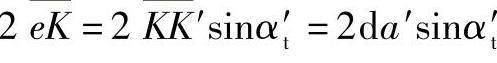
为了消除侧隙，可使轮齿在基圆r_b2弧上的齿厚s_b2（即基圆r_b2弧上，轮齿渐开线间的距离）增大ds_b2=2da′sinα_t′，或者使小齿轮和大齿轮的弧齿厚s_b1、s_b2同时增大：

ds_b2±ds_b1=2da′sinα′_t （2-17）

式中，“+”号用外啮合，“-”号用于内啮合。

在内啮合传动中，s_b2为基圆r_b2弧上形成齿槽的距离。当无侧隙时，中心距的正增量da′会引起卡住现象，即产生负侧隙。要避免这种情况，应使ds_b2-ds_b1之差具有正值。

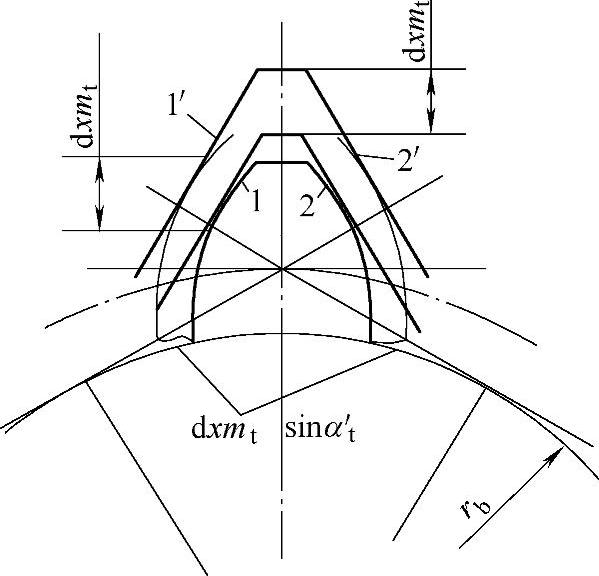
图2-11 基本齿廓位移对齿厚的影响

图2-11所示为齿条和轮齿渐开线1与2相啮合时的情况。令齿条位移值为dxm_t，则轮齿渐开线齿形和齿条位移后的新啮合位置为1′和2′，同时齿条位移dxm_t后，将引起轮齿渐开线之间在基圆弧上的距离s_b增大，其大小为

ds_b=2dxm_tsinα′_t

如果相啮合的一对齿轮，其小齿轮和大齿轮相对于齿条基本齿廓的位移增量分别为

dx₁m_t和dx₂m_t，则在基圆r_b1、r_b2上的轮齿渐开线之间弧长增量的总和为

ds_b2±ds_b1=2dx∑_tm_tsinα′_t （2-18）

由式（2-17）、式（2-18）得

又从式（2-15）知

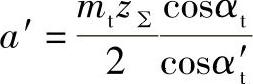
则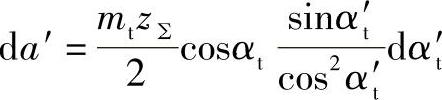

代入式（2-19）后，得

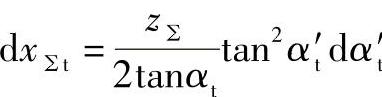
如果随着中心距的变化，啮合角从α_t相应变化到α′_t，则将上式积分，得

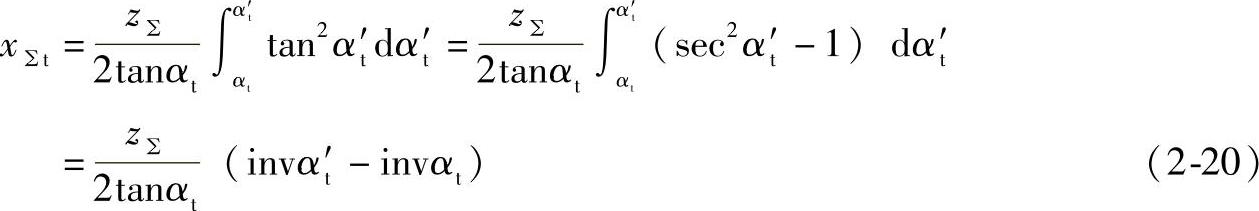
或

从式（2-19）中，可以明显地看出

dx_∑tm_t>da′

因此 x_∑tm_t=a′-a=y_tm_t （2-21）

即 x_∑t＞_yt或x_∑n＞y_n

现引用代号表示

x_∑-y=Δy （2-22）

x_∑t-yt=Δy_t （2-23）

或x_∑n-yn=Δy_n

Δ_y、Δy_t、Δy_n分别为直齿、斜齿圆柱齿轮的齿顶高变动系数。式（2-22）用于直齿轮传动（β=0）；式（2-23）用于β≠0的斜齿轮传动。

由式（2-16）和式（2-20）得

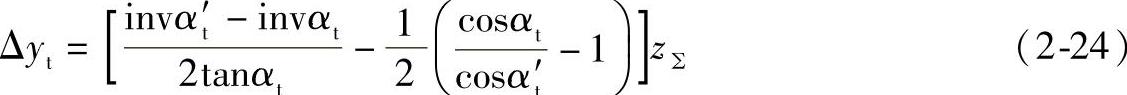
当β=0、α_t=α时，则式（2-24）为

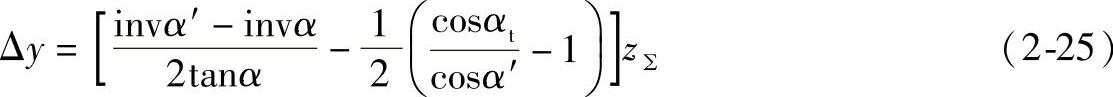
由此可见，采用上述公式进行角度变位传动计算是相当复杂的，这就是推荐用线图法计算的原因所在。

现将有关线图介绍如下，图2-12绘制出与z₁、z₂相关的允许的最大齿顶高变动系数Δy值的关系曲线。可根据z₁和齿数比u=z₂/z₁查图2-12线图得Δy值。

按图2-12确定的Δy值（或相应的x∑值）是允许的最大角度变位，即符合封闭图许用区范围，因而不必验算根切、齿顶变尖、重合度和干涉条件等。

图2-13、图2-14是根据无侧隙啮合方程绘制的z∑和x∑与Δy、α′_t的关系曲线图；图2-15、图2-16是根据z∑和y确定Δy值的线图；图2-17是压力角α=20°时，由x_∑和z_∑来确定端面啮合角α′_t的线图。应用查线图计算角度变位的几何参数x_∑、y、α_t′（α′）、Δy_t（Δy）值，与用繁杂的无侧隙啮合方程式计算相比，其计算工作量大为减少。尤其适用于行星齿轮传动的设计。应该指出计算角度变位参数是足够精确的，经多次计算表明，查线图线图过程中，除当在两曲线之间插值时，可能出现误差外，其几何计算误差也只有公法线长度公差值的1/3。

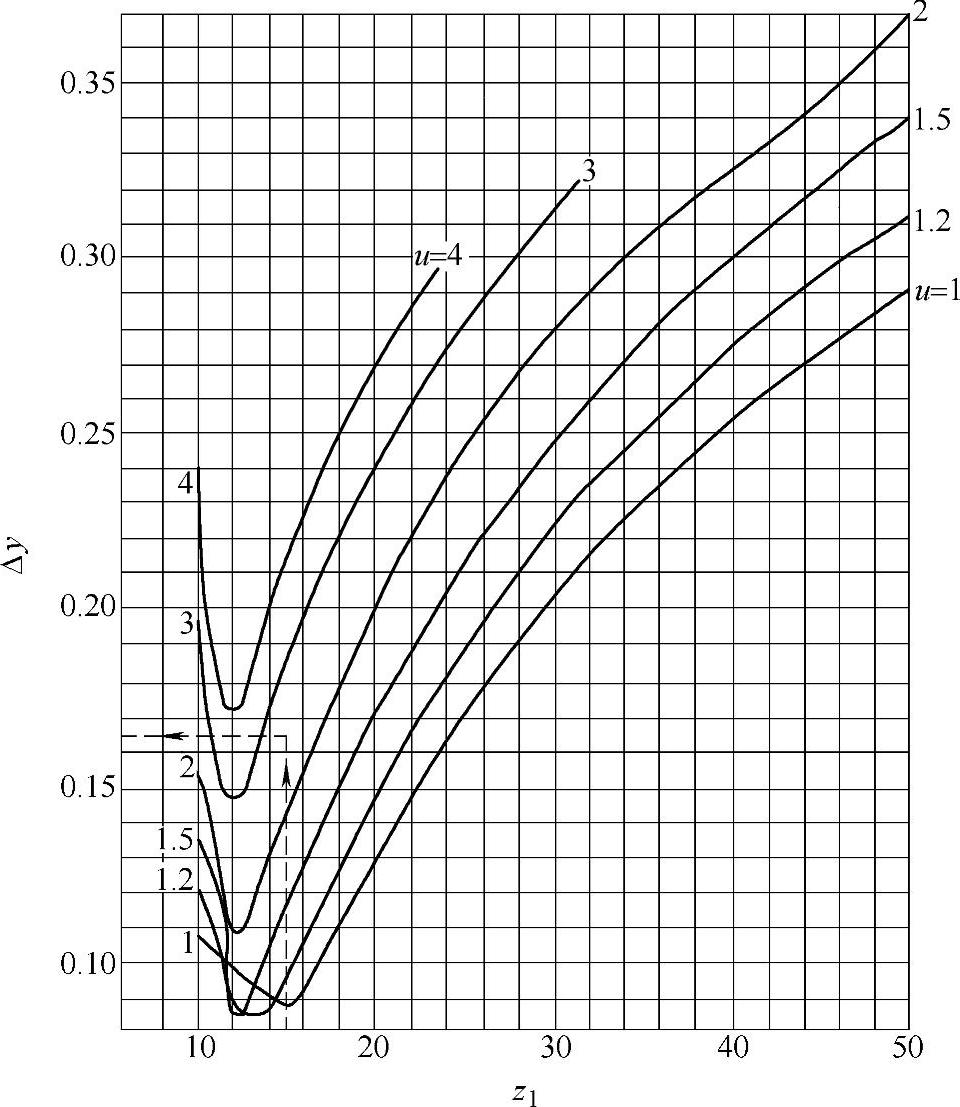
图2-12 根据z₁和齿数比u=z₂/z₁确定Δy值之线图

例：已知z₁=15，u=z₂/z₁=2.53，查线图得Δy=0.165（见图中虚线所示）。

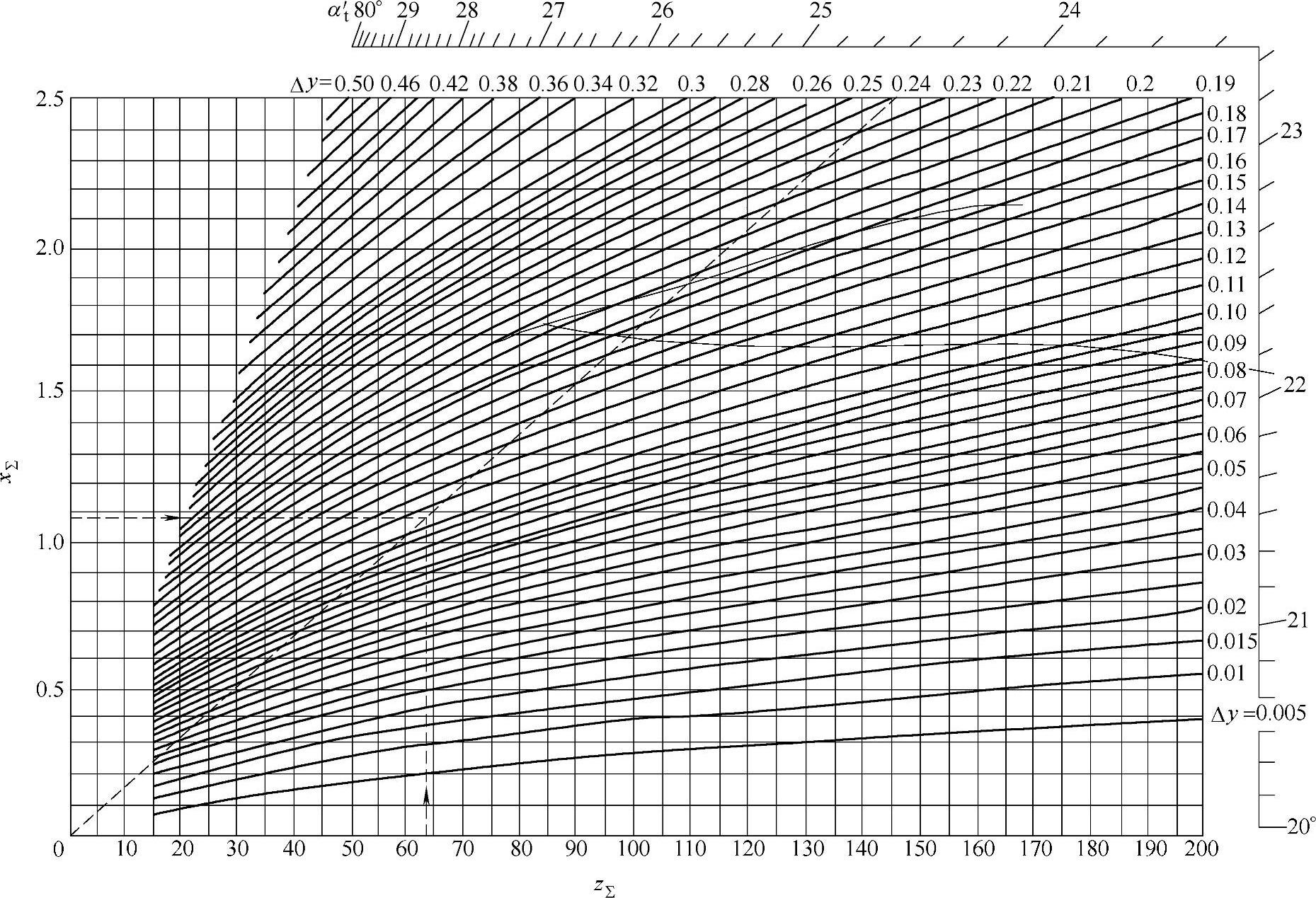
图2-13 当x_∑＞0时，根据z_∑和x_∑确定Δy及α_t′之线图(www.daowen.com)

例：已知z_∑=63，x_∑=1.08，查线图得Δy=0.105（见图中虚线所示）。从0点及z_∑=63、x_∑=1.08之标点连一直线，可得端面啮合角α′_t=24°20′。

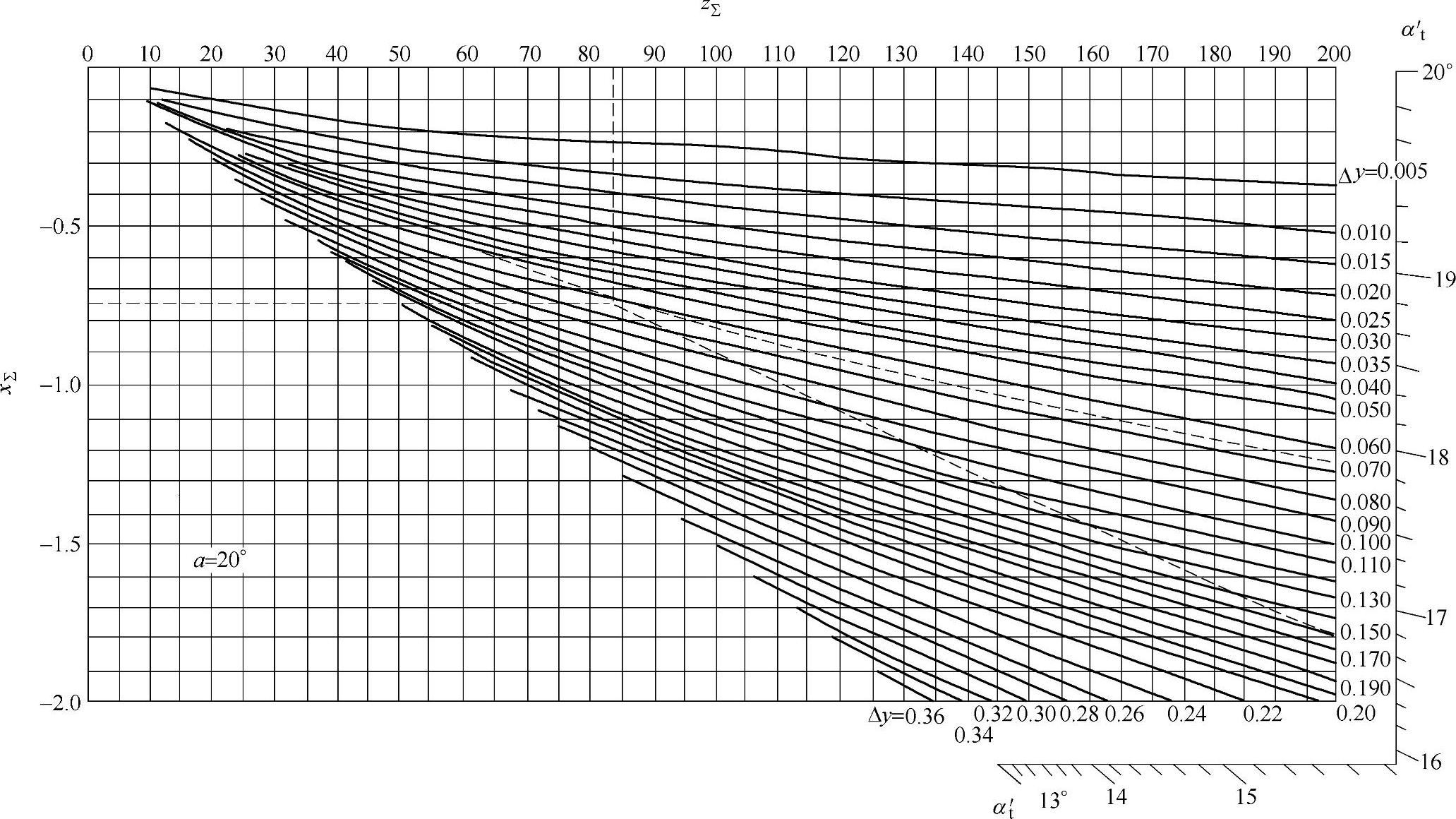
图2-14 当x_∑＜0时，根据z_∑和x_∑确定Δy及α_t′之线图

例：已知z_∑=83，x_∑=-0.75，查线图得Δy=0.065和α_t′≈16°38′（见图中虚线所示）。

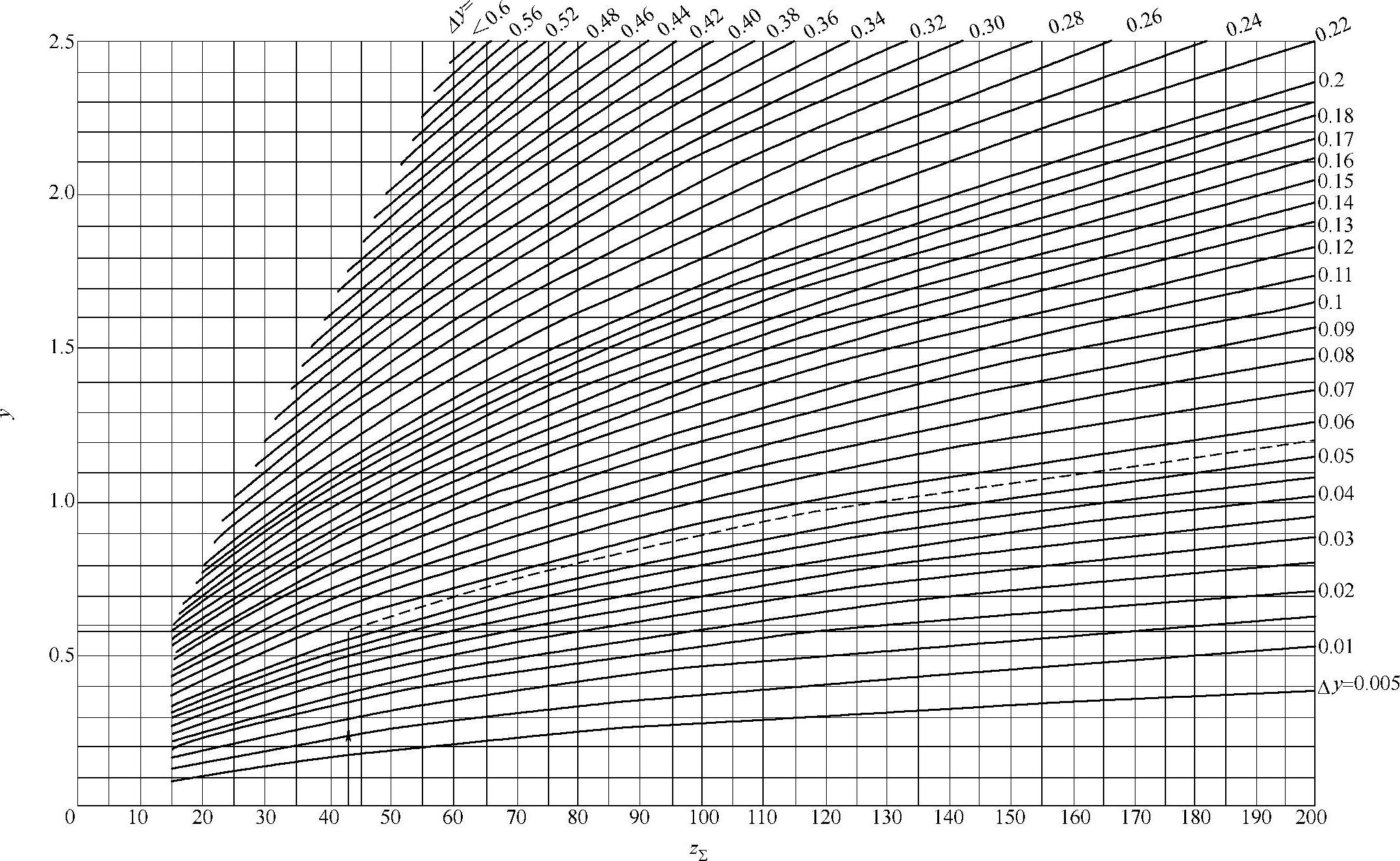
图2-15 当y>0时，根据z_∑和y确定Δy值之线图

例：已知z_∑=43，y=0.59，查线图得Δy=0.055（见图中虚线所示）。

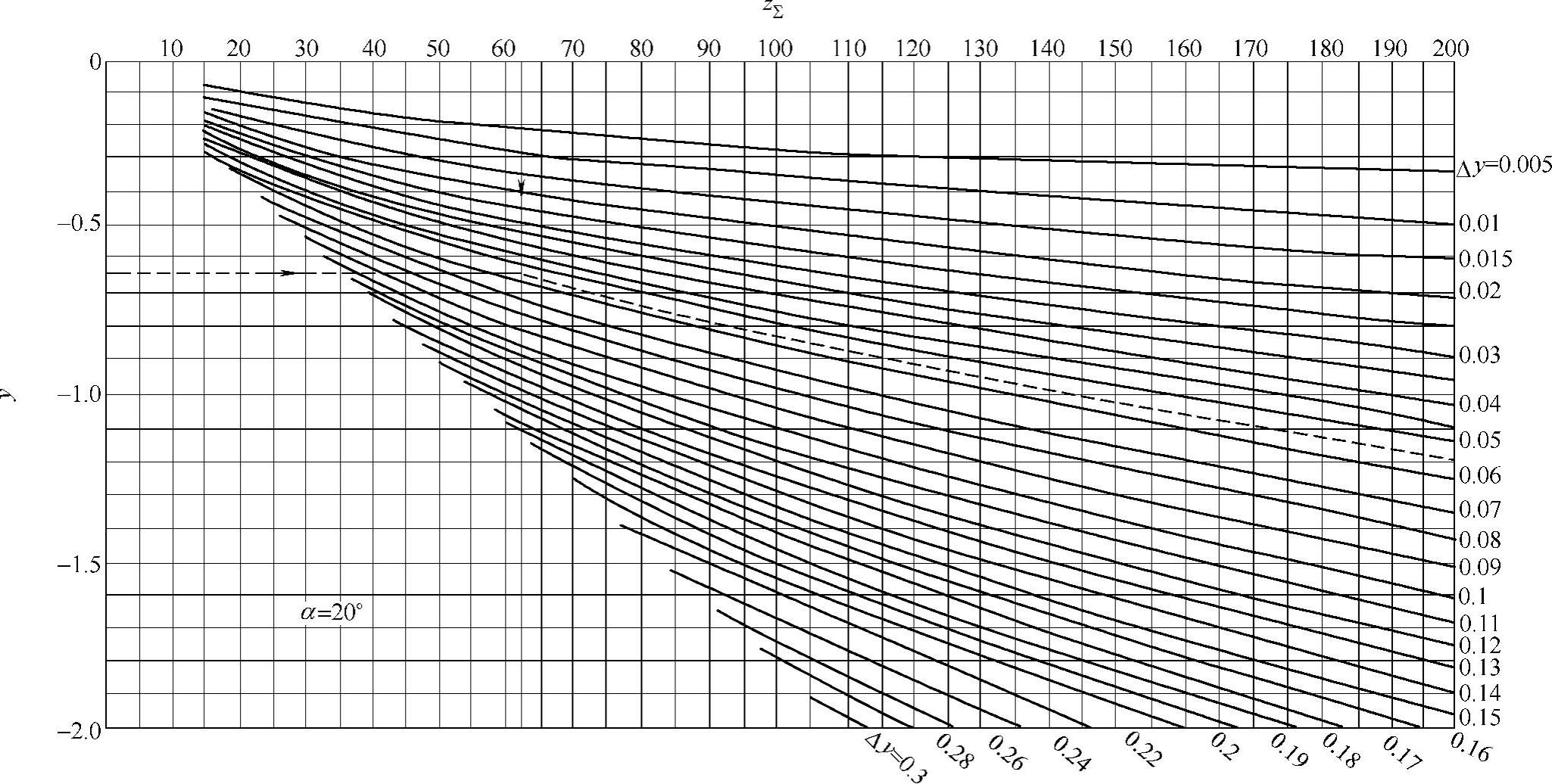
图2-16 当y＜0时，根据z_∑和y确定Δy值之线图

例：已知z_∑=62，y=-0.65，查线图得Δy=0.055（见图中虚线所示）。

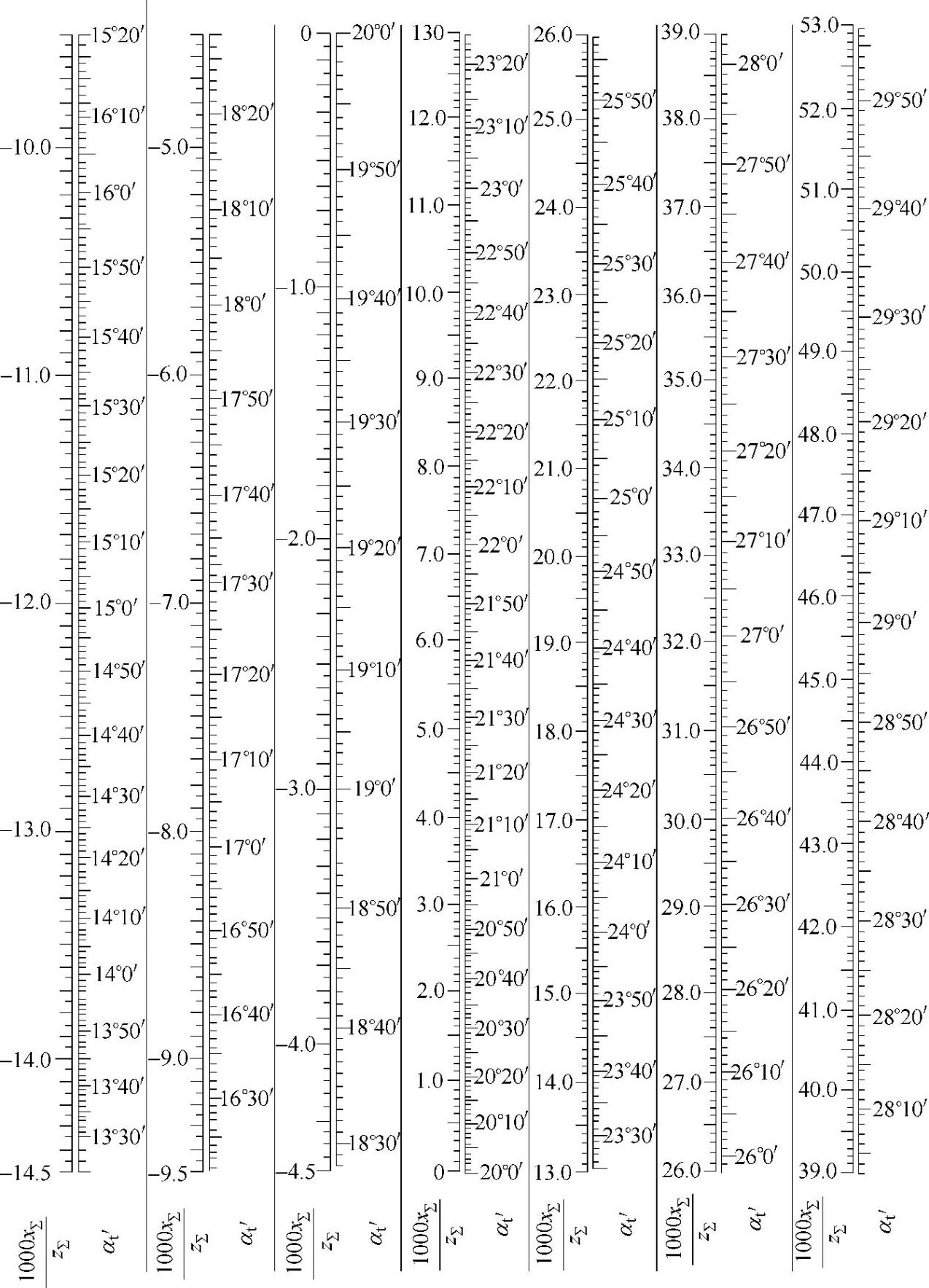
图2-17 当压力角α=20°时，由x_∑和z_∑来确定端面啮合角α_t′之线图

例：已知z_∑=59，x_∑=1.75，试确定α_t′。由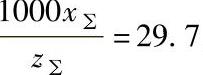，查线图得α_t′=26°36′。

对斜齿圆柱齿轮传动来说，可分两种情况：

1）已知z_∑、x_∑及β，求中心距a′。先利用图2-13或图2-14之线图确定Δy值，再按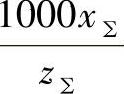值和β值，由图2-18之线图确定μ值，然后按下式计算Δy_t：

Δy_t=Δy-μz_∑ （2-26）

最后求出中心距变动y_t=x∑_t-Δy和中心距a′

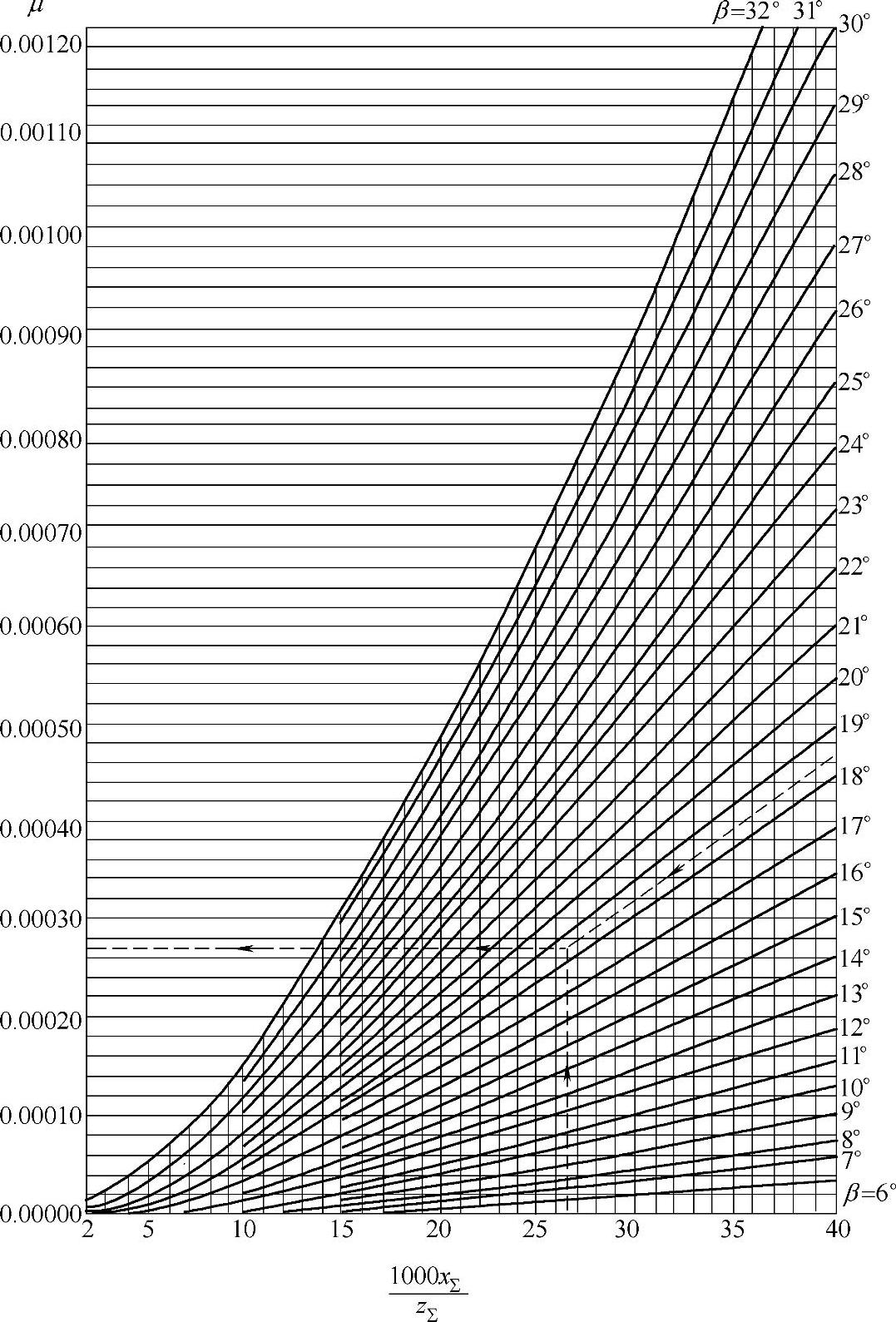
图2-18 确定斜齿圆柱齿轮计算系数μ的线图

例：已知z_∑=49、x_∑=1.3、β=18°30′，确定μ值。根据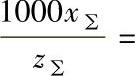26.5、β=18°30′，由线图查得μ=0.00027（见图中虚线所示）。

a′=a+y_tm_t=（0.5z_∑+x_∑t-Δy_t）m_t （2-27）

2）已知α′、z_∑和β，确定x_∑t。

先由下式求得

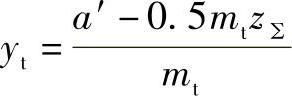
并按y、z_∑值由图2-15或图2-16的线图确定Δy值，以及根据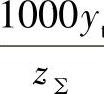t值与β值，由

图2-19 之线图求得ω值，然后由下式确定Δy_t：

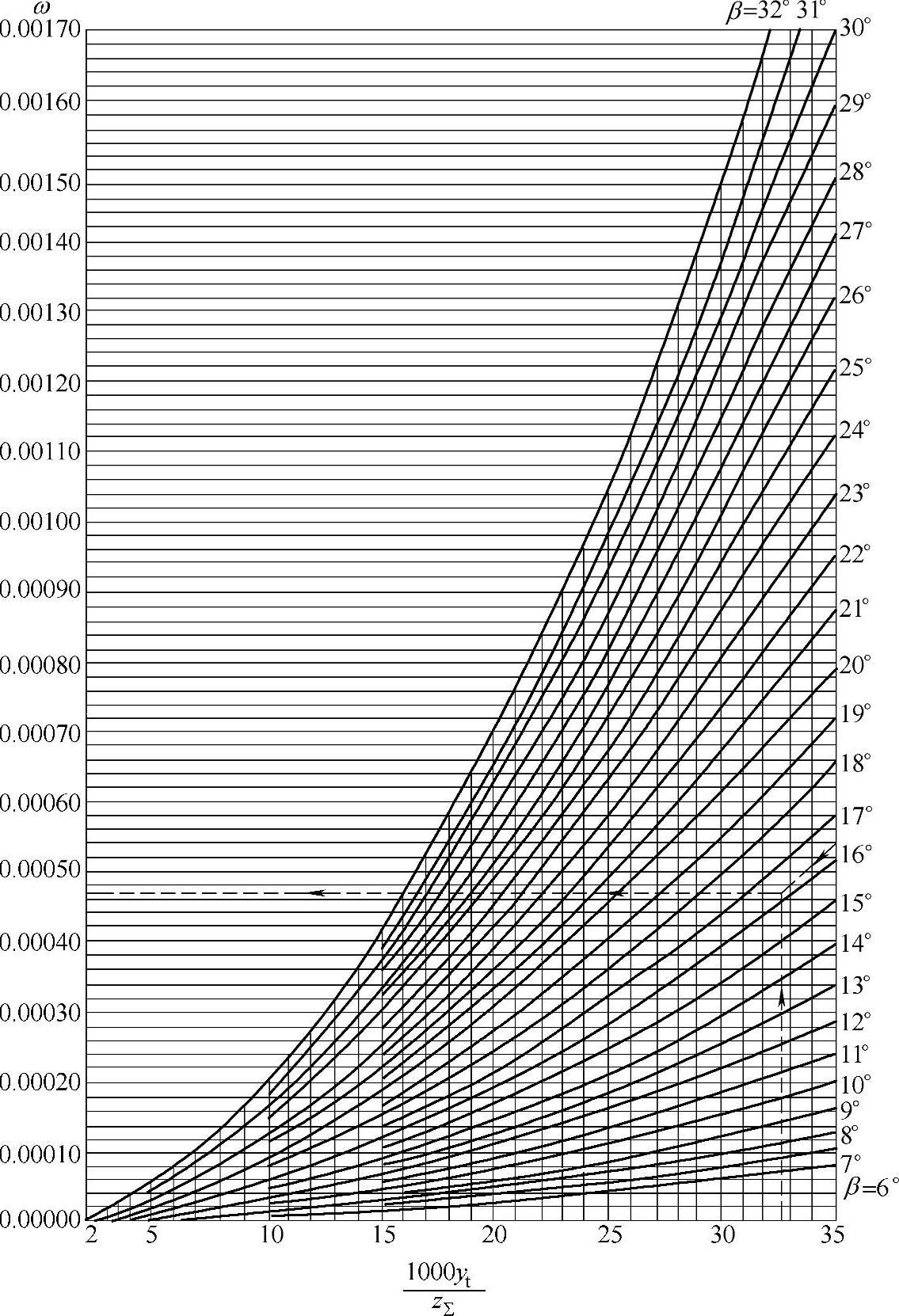
图2-19 确定斜齿圆柱齿轮计算系数ω之线图

例：已知z_∑=40、a′=213、β=16°20′、m_t=10，确定ω值。根据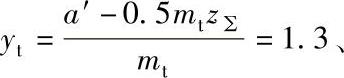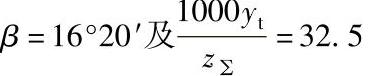，查线图得ω=0.00047（见图中虚线所示）。

Δy_t=Δy-ωz_∑ （2-28）

最后求得总变位系数x_∑t

x∑_t=y_t+Δy_t （2-29）

对于行星齿轮传动的变位设计，推荐用线图法进行计算，既方便，又不会算错，即使反复计算也很快。今以2K-H（NGW）型行星齿轮传动为例，说明其计算步骤。

在图2-20所示的行星齿轮传动中，根据传动比要求、同心条件、邻接条件和装配条件等要求，进行初配齿数，得太阳轮齿数z_a、行星轮齿数z′_g、内齿圈齿数z_b，然后按下列步骤进行变位计算：

1）确定角变位的行星轮齿数z_g

①由小齿轮齿数z₁（z_a或z′_g）及齿数比u′_ag=z′g（当z_a＞z′_g

za

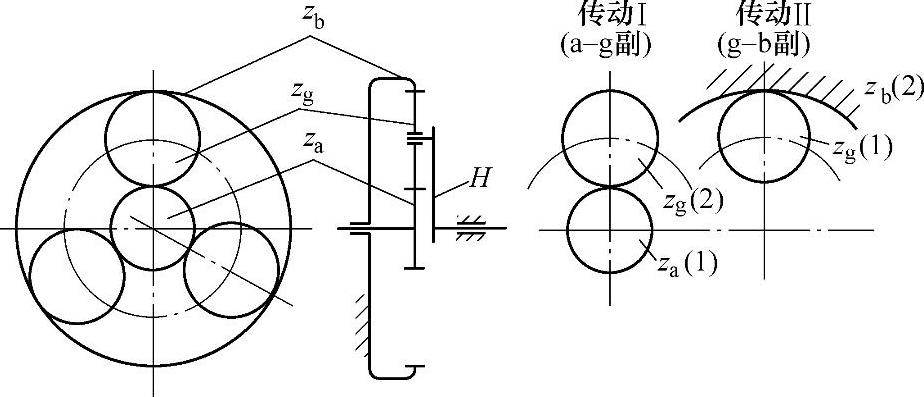
图2-20 2K-H（NGW）型行星齿轮传动简图

时，则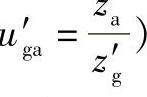，查图2-12线图得Δy′值。

②由z′_∑ag=z_a+z′_g及Δy′值，查图2-13或图2-14线图得x′_∑ag值。

③z_g=z′_g-（x′_∑ag+0.2），按四舍五入取整数确定行星轮齿数z_g。

2）确定实际中心距a′_ag

①由z_∑ag=z_a+z_g及Δy′查图2-15或图2-16线图得y′值。

②a′_ag=a_ag+y′m，偏小取整数确定实际中心距a′_ag。

3）传动副I（a-g副）角变位几何参数的计算

①由z_∑ag及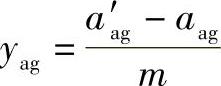，查图2-15或图2-16线图，得Δy_ag值。

②x_∑ag=y_ag+Δy_ag

③根据滑动率相等原理，按下式分配变位系数：

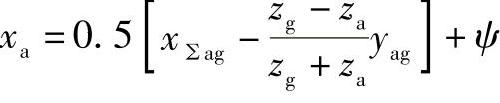
式中，当太阳轮相对于行星架是主动时，取ψ=0.08～0.12，通常取ψ=0.10；当太阳轮相对于行星架是从动时，取ψ=0～0.04。

而x_g=x_∑ag-xa

④按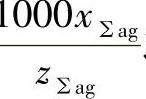之值查图2-17线图，得啮合角α′_ag。

4）传动副Ⅱ（g-b副）角度变位几何参数的计算

①按同心条件得a′_ag=a′_gb，由z_∑gb=z_b-z_g及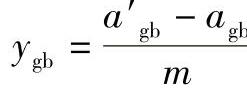，查图2-15或图5-16之线图，得Δy_gb值。

②x_∑gb=x_b^-xg=y_gb+^Δy_gb

③x_b=x_∑gb+x_g（x_g采用a-g副计算确定的数值）。

④根据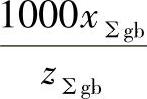，查图2-17线图，得啮合角α′_gb。

在行星齿轮传动中，由行星齿轮传动的同心条件得知，两对啮合副（a-g副，g-b副）的中心距必须相等，即a′_ag=a′_gb。因此，传动副I（a-g副）采用较大的正角度变位，传动副Ⅱ（g-b副）也必然是大的正角度变位。这时，内齿圈的变位系数x_b较大，会过于削弱内齿圈的弯曲强度，这是不利的。通常，将初定的行星轮齿数z_g′减少1～2个齿，再进行角度变位，这样可使a-g副具有尽可能大的正角度变位，其啮合角α′_ag=22°～26°，而g-b副为高度变位或负角度变位，啮合角α′_gb=17°～20°为宜。