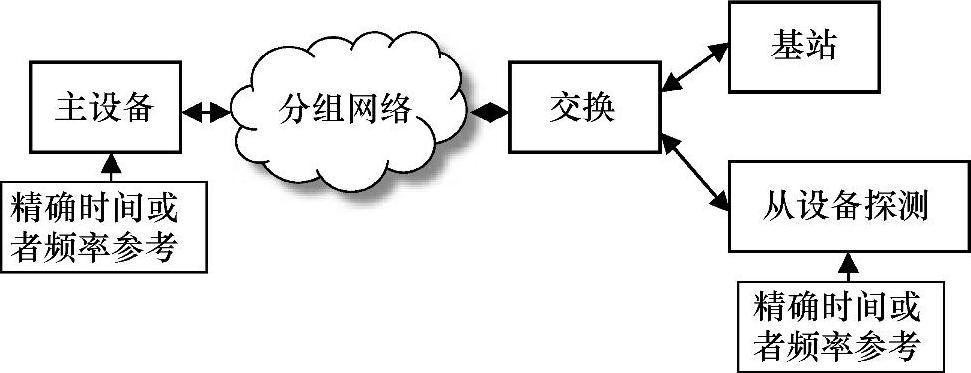
图6.20 分组延时测量

正如以前所显示的，TDM测量的原始素材是时钟的时间误差。对分组时钟来说，计时分组的延时变化引起时间误差。因而，对相应的分组计时测量来说，能直接使用分组延时作为原始数据。例如，使用图6.20中的建立方式，能测量延时。由于两端的准确时间参考或者频率参考，图6.5中的所有时间戳t₁～t₄都是准确的，并且都能被探测从端知道。如果这个参考是频率参考，那么绝对延时不能计算得到。然而在频率同步的例子中，这些并不重要。

正如早期提到的，对基于分组的频率同步来说，分组选择尤为关键。因而，在分组选择中一直引入基于分组的频率同步测量。如图6.21所示，有两种选择方式：一种是测量计算本身集成分组选择；另外一种是分组预选取并且创建一个作为实际测量基础的新数据集。

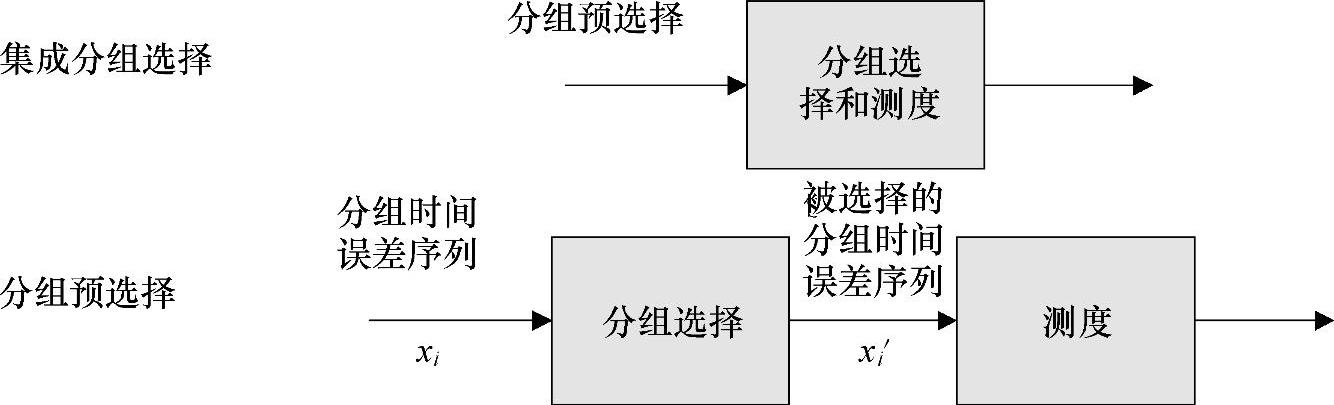
图6.21 测度模型

第二个选择模型与多个分组时钟的选择模型类似。因而，在分组延时变化（Packet Delay Variation，PDV）公差规格方面，通常使用该模型。由于本书内容限制，仅在如下内容中讨论该模型。

网络负载通常是PDV的最主要影响。负载有一个强24h循环模式。因而，典型地，延时测量持续至少24h。分组时间误差序列包含几十万～几百万的数据采样。对分组选择来说，使用同等长度的时间窗口依次分割采样数据，并且从这些分割组中选择一定比例的最快分组。为了从每一个时间窗口中产生一个单一的延时值，平均计算被选择的延时。这个是最通常被使用的预处理方法。也有其他方案，但不在这里讨论。图6.22显示了被选择分组时间误差序列与原始序列相比明显有更小的延时噪声。

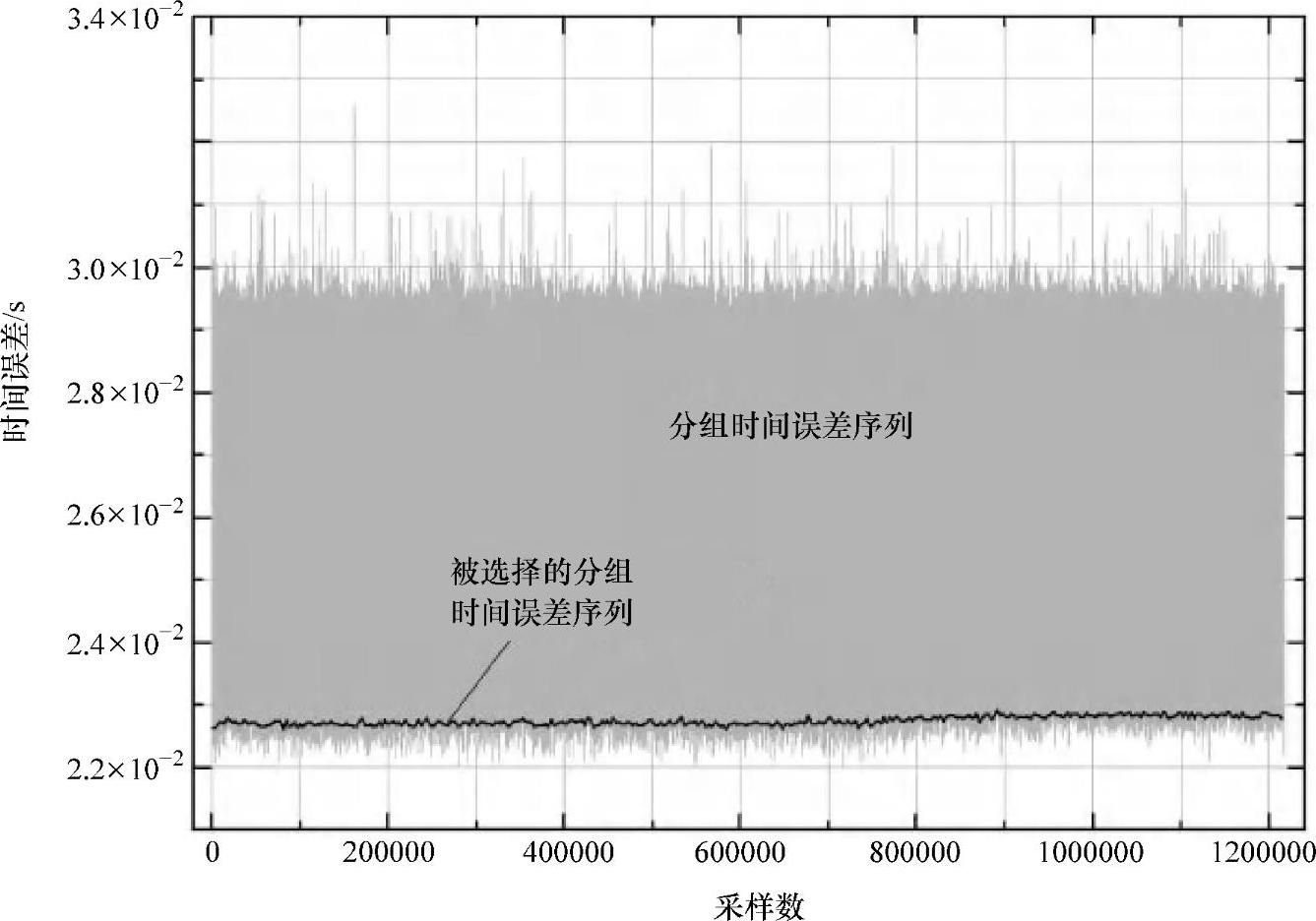
图6.22 时间误差序列和被选择的时间误差序列

6.5.2.1 TDEV

比如，预处理后TDEV或者MDEV能被计算。被选择分组时间误差序列的TDEV值与高于时钟算法平均计算性能的τ值点的分组时钟计算得到的TDEV值完全一致，具体如图6.23所示。虽然预处理延时计算得到的TDEV值很好地估计了时钟输出的TDEV值，但是不考虑使用这种测量方法作为分组时钟的公差规范。这是因为TDEV平均计算了整个测量周期内的扰动，并且不能描述最大可允许的扰动。

6.5.2.2 MATIE和MAFE

正如图6.23所示，两条曲线几乎重叠。也就是说，在滑动窗口（图6.10的灰色列）内的平均计算与分组时钟出现的平均计算相类似。因而，可以设想使用两个相邻平均计算窗口的相位差异估计在微调算法中使用相应平均计算的时钟相位变化，如图6.24所示。通过滑动两个窗口以及计算最大差异（而不是平均计算作为TDEV的外部和），获取最大相位变化估计或者最大频率误差。

使用式（6.9）去计算预处理延时序列用以得到最大相位改变或者最大平均时间间隔误差：

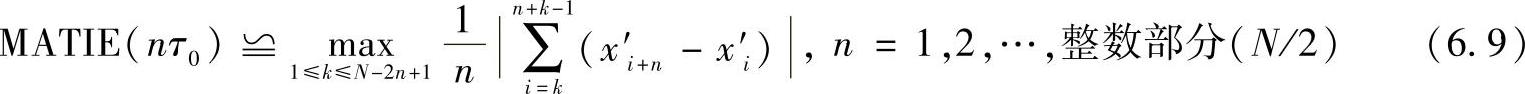
当与MTIE和TDEV公式相对比时，发现MATIE是由两者混合而成。最大平均频率误差由式（6.10）计算得到：

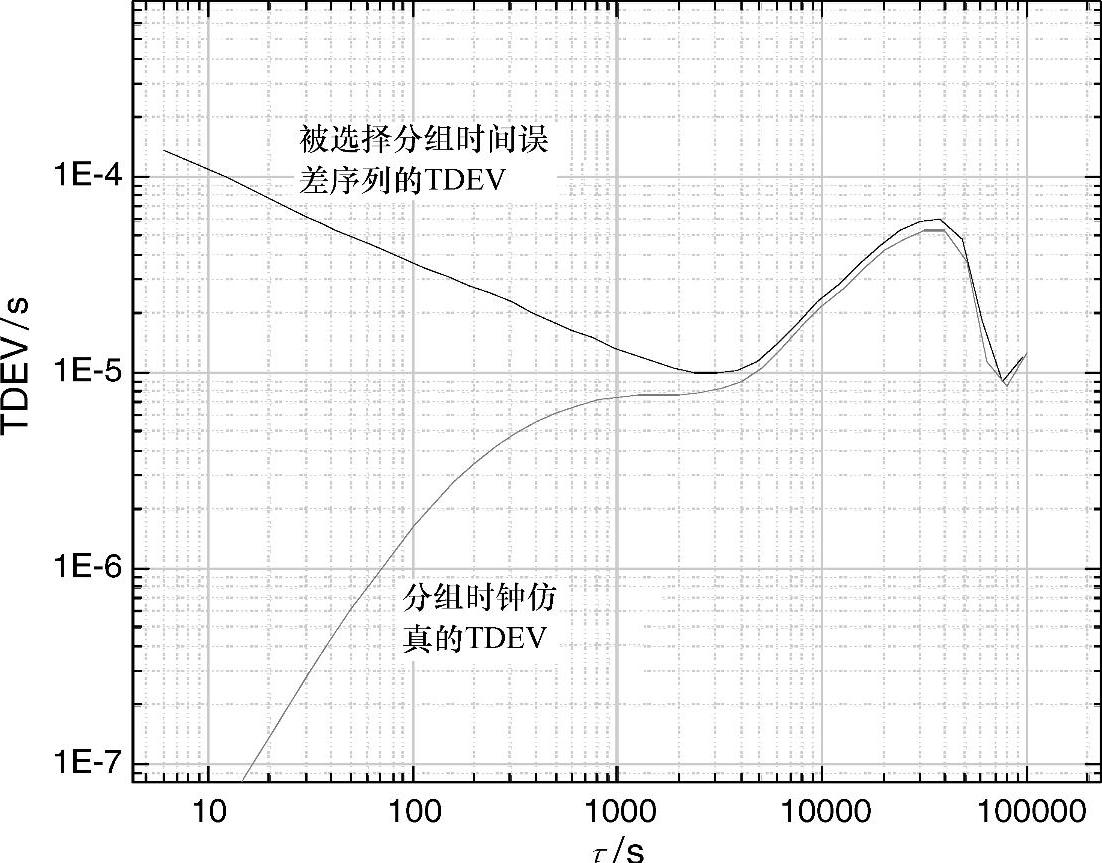
图6.23 分组时间误差和分组时钟的TDEV

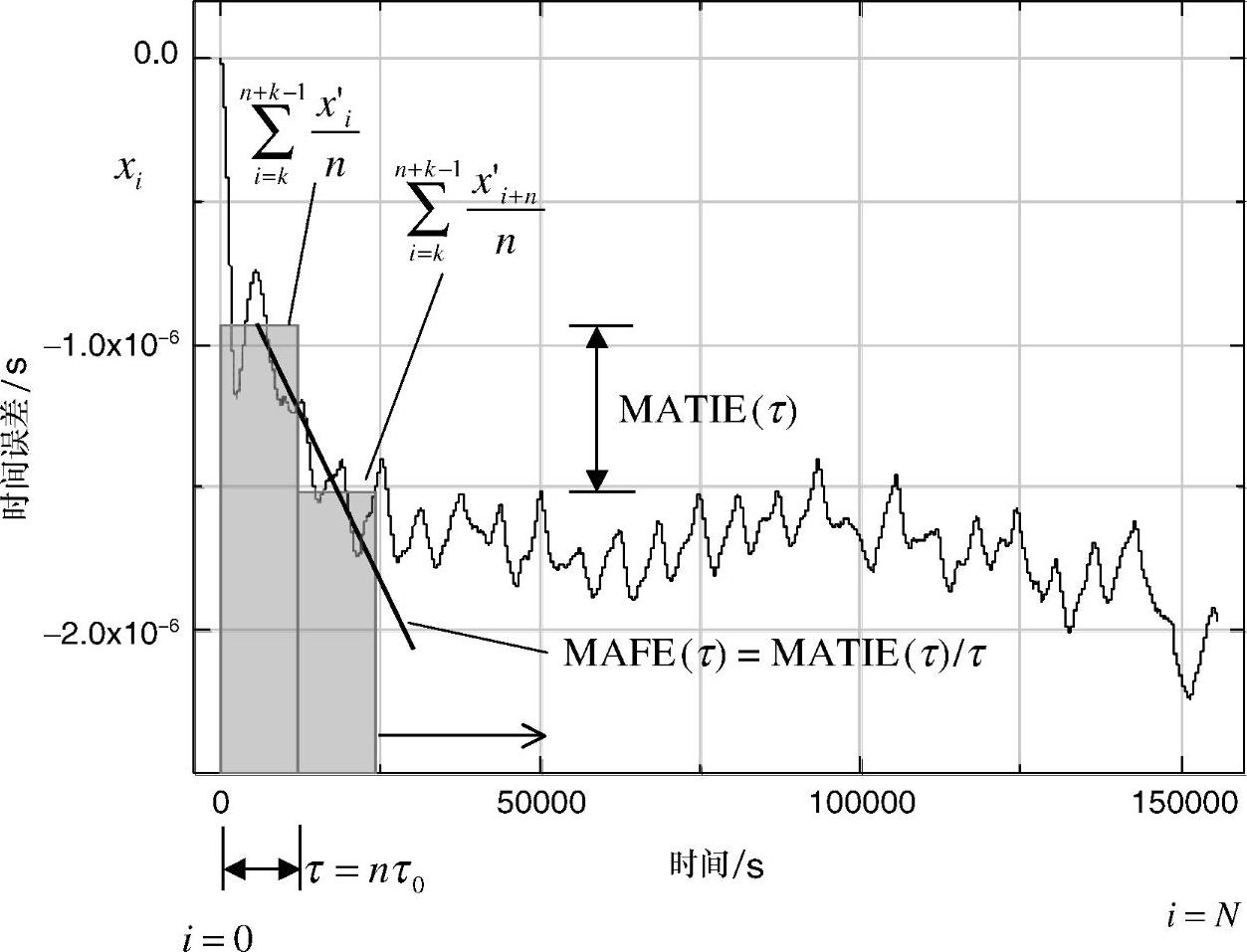
图6.24 MATIE和MAFE计算原理

(www.daowen.com)

图6.25显示了类似于图6.22中的分组延时序列的计算曲线。正如在TDEV的情形下，从被选择分组时间误差序列和分组时钟计算得到的曲线在τ值位于时钟过滤能力之上互相完全一致。请注意，对基站内部时钟来说时钟的频率未定型并不足够。刚好一个例子显示了这种相关性。被选择分组延时序列上，针对不同的过滤频段进行时钟仿真测试。观察到源于每一个时钟的最大频率误差（τ_estimate）存在线性关系，但不是像PLL滤波时间常数那样的1∶1关系。因而，原则上讲，时钟最大频率误差能从时钟的时间常数和被选择分组时间误差序列的MAFE曲线中估计出来。

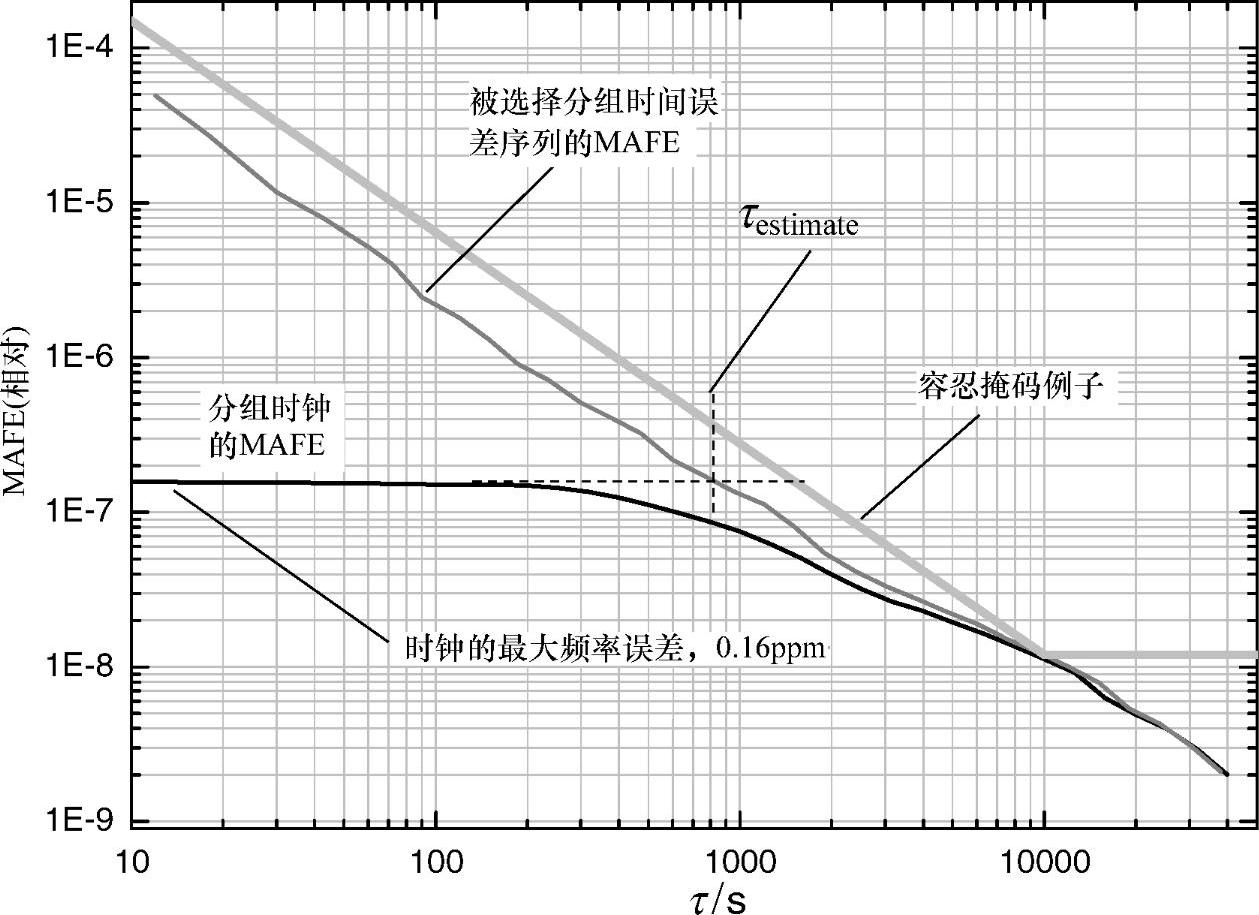
图6.25 被选择分组时间误差序列和分组时钟的MAFE

浅灰色曲线是这种延时噪声级别条件下能达到16ppb精度的时钟容忍曲线的一个例子。大约需要10000s平均计算的能力。因而，在曲线的10000s处存在一个拐点。对给定的延时抖动和晶体振荡器漂移边界条件，精度级别处在12ppb上。斜率能在影响算法的时间比例因子中体现出对噪声的限制。

6.5.2.3 pktfilteredMTIE

TDM网络中，最经常使用的测量是MTIE。因此，如果能在公差规范中使用MTIE，它将是测量的选择。图6.26中描绘了各种各样的MTIE曲线。很明显地看出，直接应用被选择分组时间误差序列的MTIE和应用时钟输出上的对应计算不相关。

然而，如果首先在被选择时间误差序列中应用滑动窗口，形势急剧变化。为了达到这个目的，在测量模型中再增加一个功能模块，“带宽滤波”，如图6.27所示。图6.26中的pktfilteredMTIE曲线描绘了应用于已使用1500s平均计算滤波处理过的数据的MTIE计算。带宽滤波公式或多或少是直接从TDEV、MATIE和MAFE公式中的滑动平均计算窗口中复制过来的，具体为

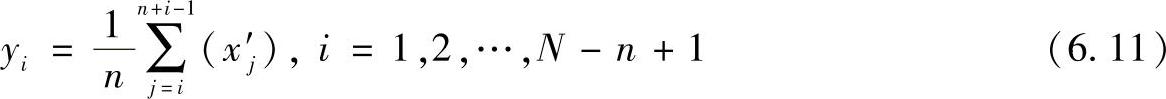
式中，变量x′_j和y_i分别是被选择和被过滤分组时间误差序列。

其他变量与TDEV公式，式（6.6）相一致。式（6.11）中使用的标记略微不同于G.8260中使用的标记，但是计算值仍旧相同。可以得出结论，pktfilteredMTIE对测试防止扩展到更长时间间隔的MTIE曲线来说非常有用，比如G.8241.5Mbit/s网络曲线和G.823SEC曲线，如图6.9所示。

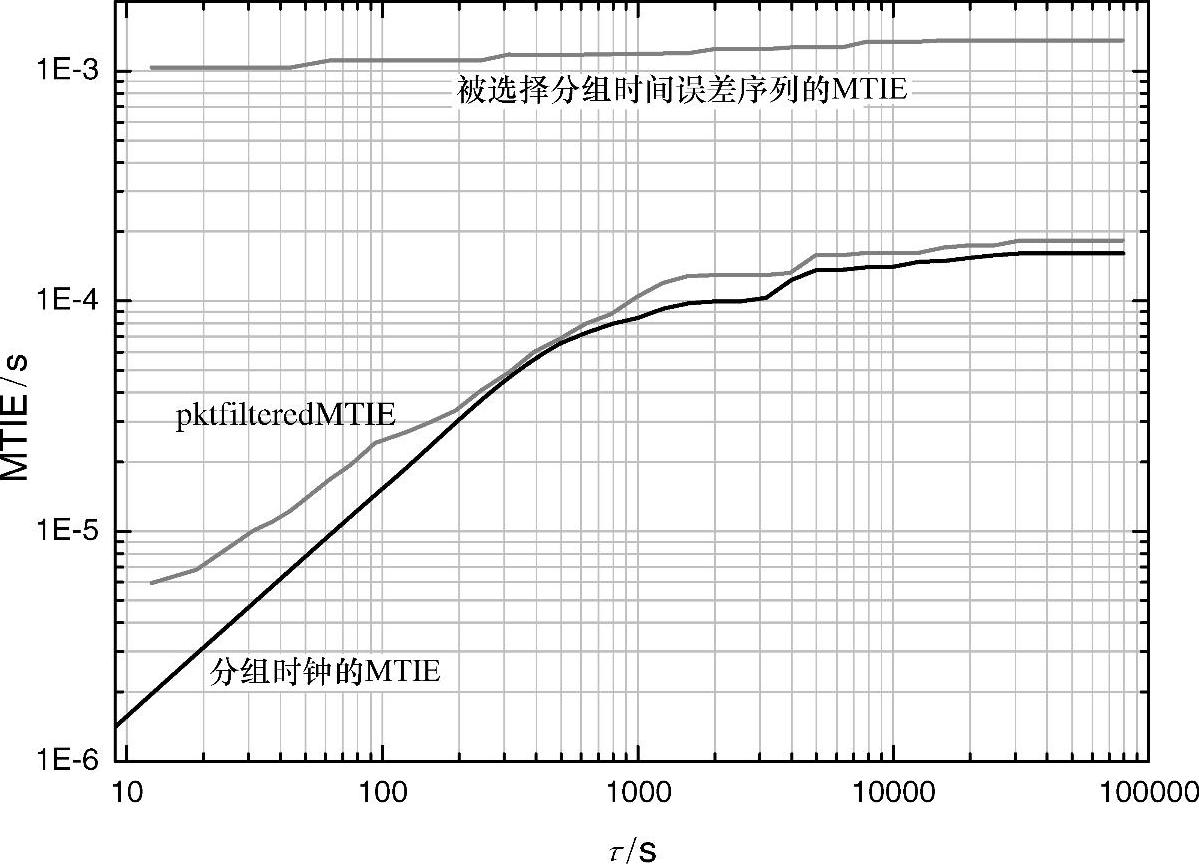
图6.26 MTIE曲线

图6.27 使用带宽滤波的测度模型

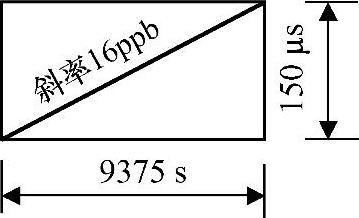
图6.28 基础延时分组传播

6.5.2.4 底层延时报文分布

度量过程中并且在最快分组的特定距离内，如果所有被选择的分组合适，就能定义需要保证16ppb的最大平均计算时间。例如，图6.28中，如果没有滤波，为了保持在16ppb误差以下0～150μs延时的斜率可能出现在9375s处或者更低位置。如果在更小的时间内出现振荡，为了保持在16ppb斜率以下，需要对延时进行滤波处理。对滤波器来说，最困难的情形是比9375s略微短并且拥有最大150μs振幅的长斜率。通过使用约9500s的平均计算窗口，能确保没有任何可能的底层延时场景引起比16ppb更大的频率偏差。

基于定义了这样的延时窗口，具体化了网络限制。参见6.3.7.3节考虑到HRM-1的网络限制，G.8261.1中采纳了这种方法。网络限制要求在每一个200s的选择窗口中，为了满足PDV限制要求，至少有1%的分组位于来自于测量的最快分组的150μs范围内。

这种方法简洁明了，因而直接作为一个测量方法被使用。实际中由于底层延时的最差场景绝不会出现，所以这种方法有些保守。分组延时一直有更容易滤波的短期变化。由于底层延时分布方法不能区分短期变化和长期变化，所有由较长时间平均计算得到的延时场景不需要被这种测量方法所接受。尽管参考模型很简单，但是150μs这个值受到很多质疑并且可能被修订。