对传输时间来说，主时钟发送时间分组到从时钟。至少有两个分组需要携带频率，如图6.13所示。要么是事先知道时间分组周期，比如自适应恢复时钟，要么就是时间分组被打上时间戳，比如PTP。如果两个时间分组发送间隔是1000s，接收两个消息之间的从时钟应该正好走1000s。如果从时钟走了999.99999s，说明从时钟慢了10ppb，故应该提高10ppb的频率。

分组经历大量的延时情况，例如由于队列原因，如图6.14所示。如果第一个分组延时2ms并且第二个分组延时4ms，那么延时差是2ms。所以，接收两个数据分组的时间间隔是1000.002s。正如前述的例子，如果从时钟慢了10ppb，从时钟需要走1000.00199s。频率比例计算产生+1990ppb的频率误差而不是正确值-10ppb。明显，这个例子中，频率误差计算精度远远不能满足要求，因而需要其他方法来计算误差。

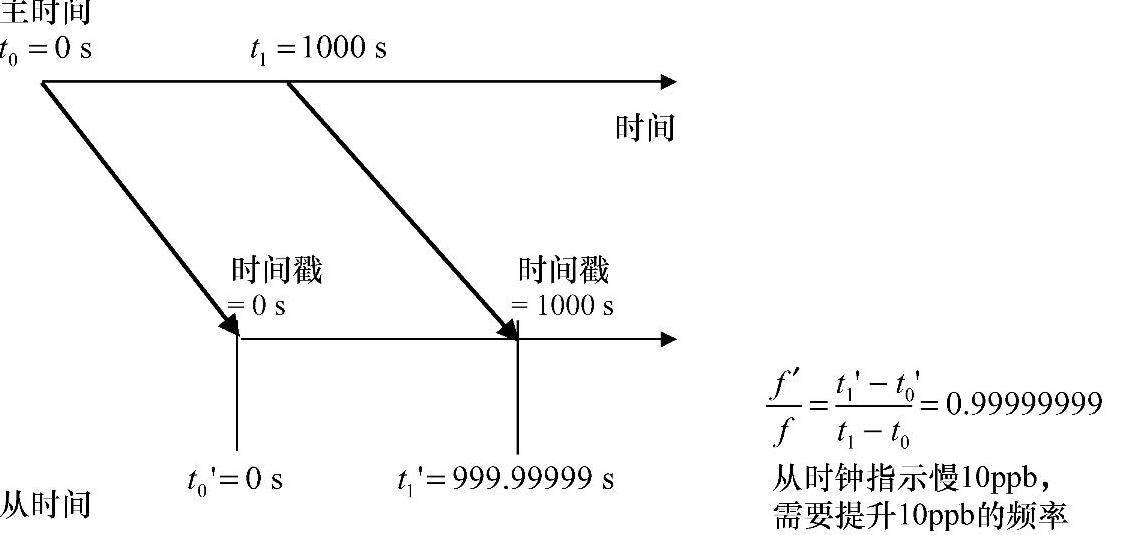
图6.13 传输频率的分组计时原理

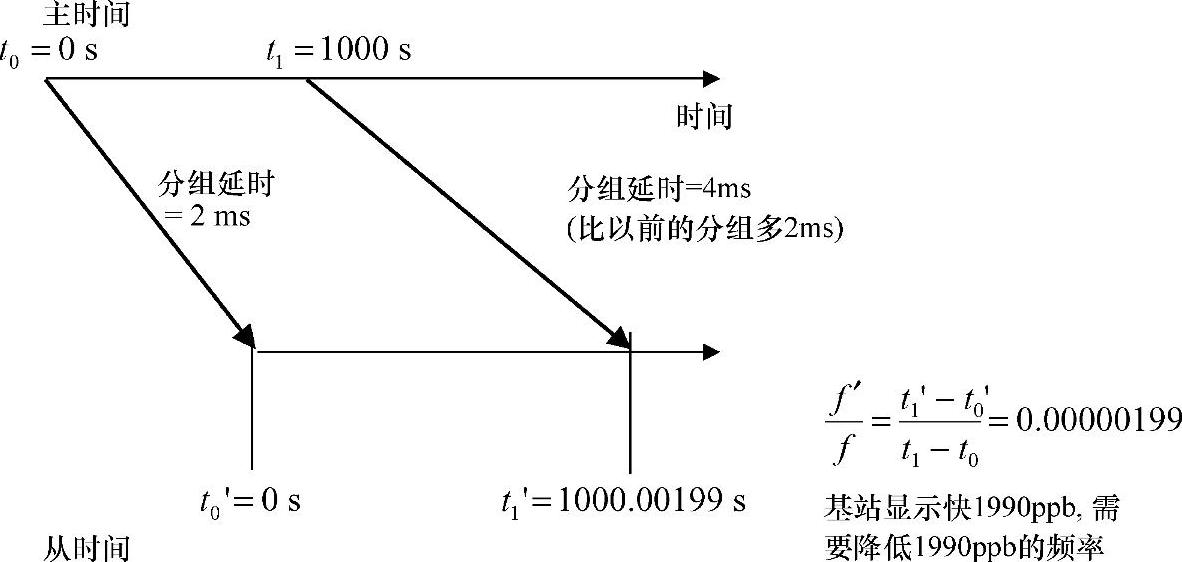
图6.14 分组延时变化对分组计时的影响

下面观测分组的延时分布以便于查清楚是否能通过选取一定比例的时间分组来提升频率误差计算。为了获取延时分布作为负载的函数，构建了一个由5个以太网交换点组成的网络，如图6.15的测量网络所示。考虑到移动传输网络的树形结构以及到达基站的业务数据在中间节点被分流的情况，需要组织数据流以便于这些数据能仿真移动传输网的数据。由于5个节点链与平均网络节点长度相比特别短，因此使用总计6万数据测量点的两份拷贝来生成比平均值大两倍的延时值，通过这种方式仿真更长的链路。首先为了去除两份拷贝数据的相关性，需要保留第二份拷贝数据点的顺序关系。这种近似可能不是首选，但是或许能得到足够精确的结果。

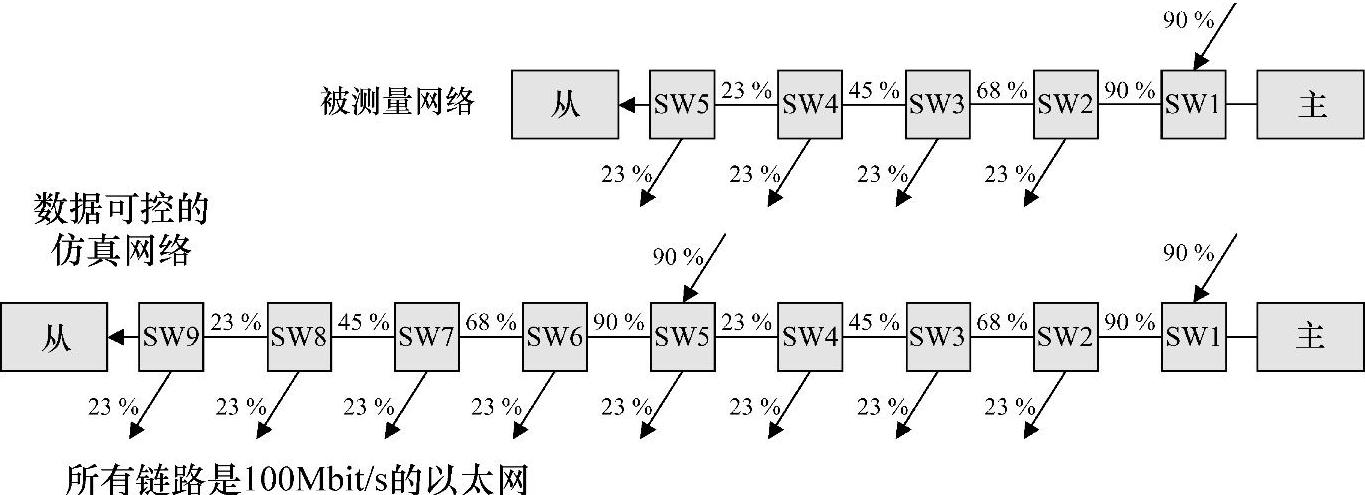
图6.15 测量和仿真网络。负载处于高负载状态。中等负载状态下，负载相应的是50%、38%、25%和13%

图6.16描述了3种负载条件下的延时分布。如果数据分组的负载在极限范围内变化，延时不确定性将是2.8ms（最低负载的最快包与最高负载的最慢包的时间差）。正如之前得出的结论，精度是不可接受的。从低负载到高负载的平均延时变化会好很多，是0.7ms，但是仍旧会产生不准确的频率误差估计。最小的延时变化仅仅有0.005ms。这个变化足够小。然而，由于低负载和高负载情况下的最小延时分组分别是每次测量中各自的最快分组，因此需要更认真的分析。

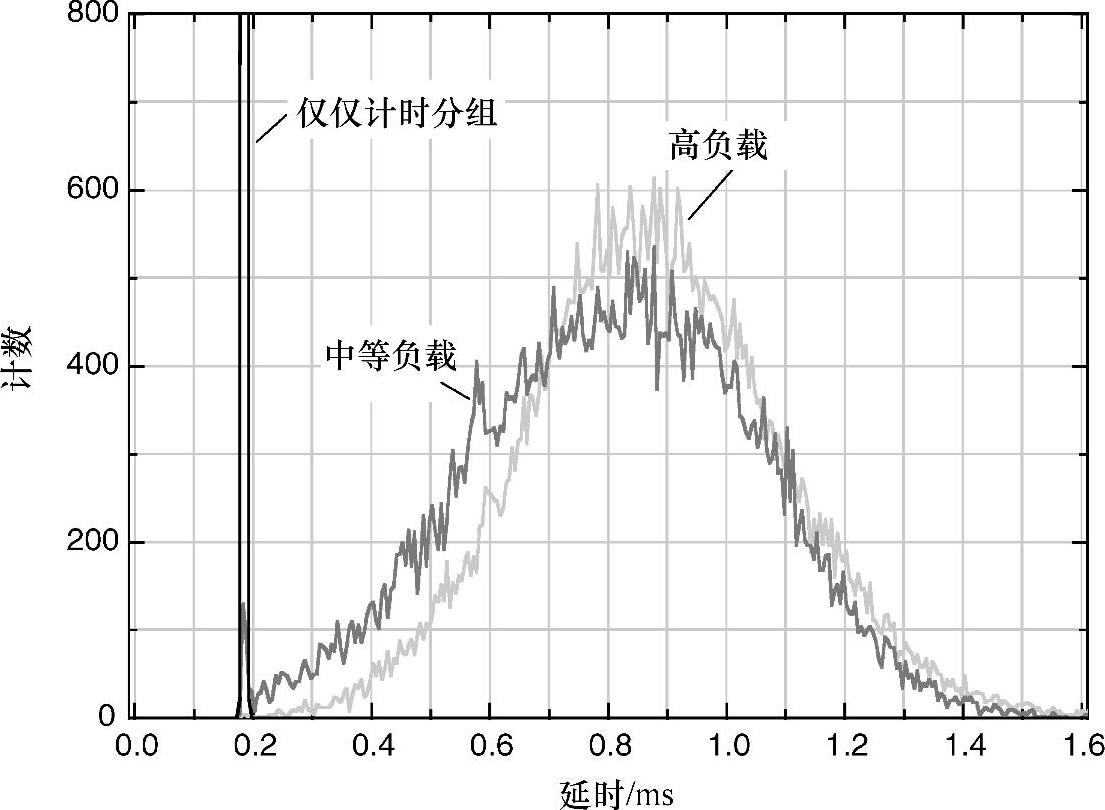
图6.16 最小、平均和最大延时：低负载-0.180ms、0.185ms和0.190ms；中等负载-0.179ms、0.810ms和1.73ms；高负载-0.184ms、0.888ms和3.01ms(www.daowen.com)

图6.17显示，仅仅是计时分组的情况下，所有6万个数据分组被限定在0.01ms的范围内。同时，在0.01ms的范围内，中等负载的情况下存在200个分组，高负载的情况下仅仅有10个分组存在。

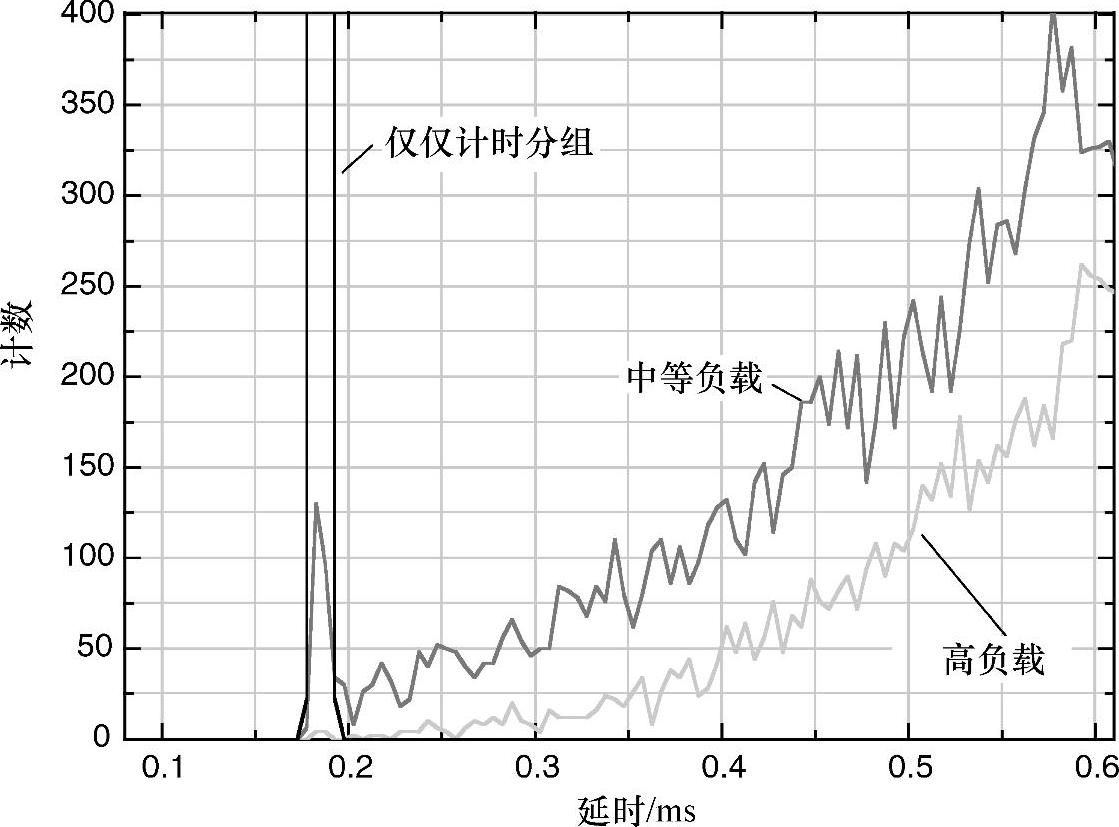
图6.17 测量的低延时尾

图6.18显示了累计分组数是如何成为延时函数的1%、0.2%和0.03%内的延时分别随着负载0.22ms、0.11ms和0.045ms的变化而变化。如果百分比内的延时平均计算，百分比内的延时不同于最小延时，分别是0.17ms、0.08ms和0.02ms。这表明平均计算降低了由于延时变化引起的误差。在测量网络中，最小延时非常稳定。在这种情况下，选择越来越小比例的包能提升性能。然而，一些传输技术，像VDSL，即使没有任何负载，仍然有延时噪声。针对这种场景，取代进一步降低百分比，最好是使用略微大一些的百分比去获取更多分组来进行平均计算。使用1%作为一个初始的折中值。虽然使用了小的选择百分比，但是为了得到足够数量的快速分组，使用16pps～128pps的典型大包速率。

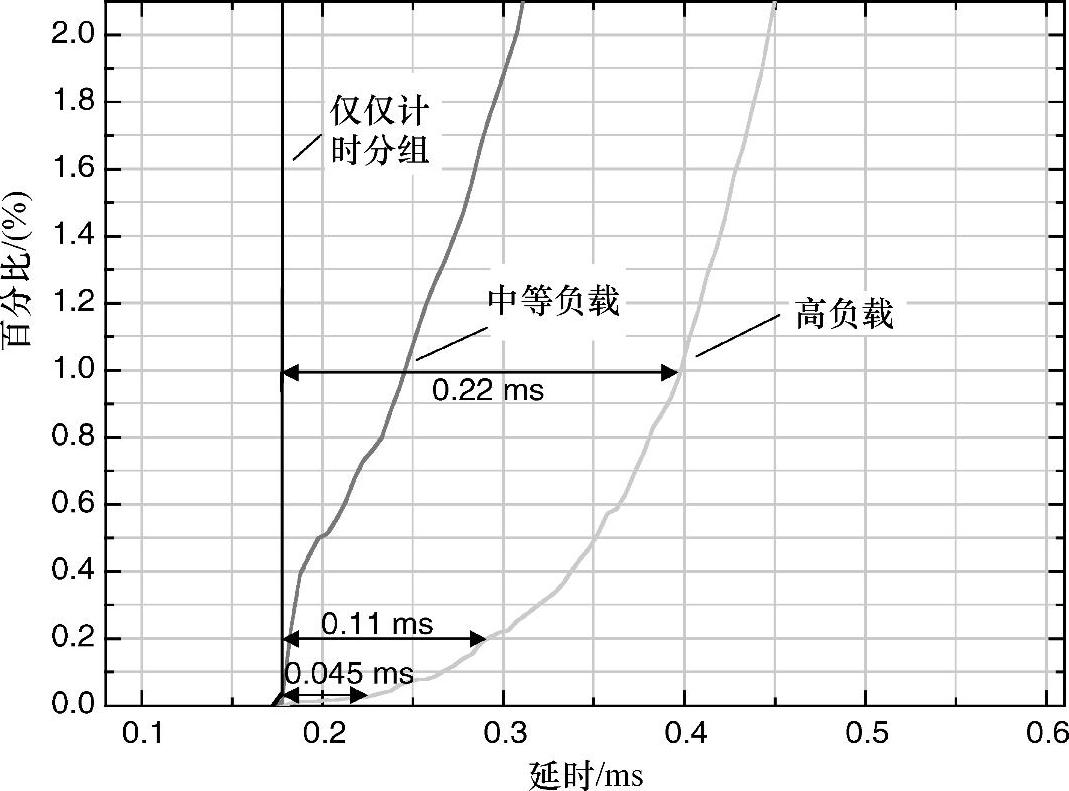
图6.18 分组作为延时函数累加

正如图6.18所示，通过使用更快的分组以及评价计算分组信息，能得到更精确的频率误差估计。经过分组选择和平均计算后，基于负载的0.17ms延时变化将产生170ppb的误差。非常不幸的是，这个误差在一段较长时间内稳定出现，进而导致早期提出的时钟平均计算算法中使用的1000s时间不够长，因而需要提升平均计算时间到10000s才能达到16ppb的误差水平。100Mbit/s链接的长链在电信行业已经成为历史。多数链接有1Gbit/s或者10Gbit/s的容量。已经说过，尤其是无线网络可能达到一个连接中有大约10个更小容量的微波无线链接下一跳。然而，在这种多个下一跳的长链路中仍旧非常确定带宽高于100Mbit/s。

图6.19展示了分组时钟的功能模型。与基于TDM的时钟模型相比较，如图6.7所示，基于分组的时钟有额外的两个部分：本地时钟比例因子和分组选择。晶体振荡器输出驱动本地时间步长，分组选择器使用本地时间信息进行分组选择。与本地时间相比拥有最大时间戳的分组是能最快地选择出来。此外，比较器时钟也改变。使用一个时间比例因子比较器去替代相位比较器或者频率比较器。正如基于TDM的时钟，比较器时钟的输出实际上可以是一个频率误差信号而不是时间误差信号。

分组同步系统中的平均计算时间可能会很长。这个时间段内，温度可能变化10多℃从而引起晶体振荡器频率漂移对算法来说太快而不能及时响应，并且也影响分组选择。因此，基于晶体振荡器对环境条件的响应，必须裁剪平均计算时间。

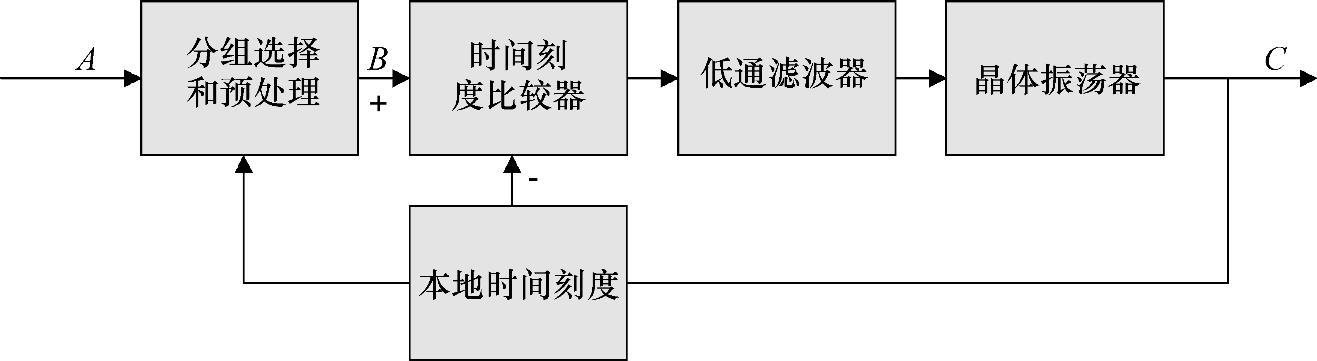
图6.19 基于时钟分组的函数模型。点A计时分组进入时钟，点B执行了分组选择和预处理，最后在点C输出