网络计划的优化，是指通过不断调整网络计划的最初方案，在满足若干既定目标的要求下，按某一衡量指标(时间、成本、资源)寻求最优的方案。例如，在人力、物力、财力有限的条件下，要求实现工期最短；又如，在工期和人力、机械、建筑材料供应等条件限定的情况下，如何安排工程的施工计划和资源供应计划，以实现工程的施工费用最低；此外还有，在一定工期条件下，怎样合理调度人力、机械、财力等各种资源的供应时间和供应强度，以实现施工现场的管理优化。总之，网络计划优化的内容包括：工期优化、费用优化和资源优化。

(一)工期优化

工期优化也称时间优化，就是当初始网络计划的计算工期大于要求工期时，通过压缩关键线路上工作的持续时间或调整工作关系，以满足工期要求的过程。

1.优化步骤

(1)计算并找出网络计划中的关键线路及关键工作。

(2)计算工期与合同工期(即要求工期)对比，求出应压缩的时间。

(3)确定各关键工作能压缩的作业时间。

(4)选择关键工作，压缩其作业时间，并重新计算网络计划的工期。

(5)当计算工期仍超过要求工期时，则重复以上步骤，直到满足工期要求或工期已不能再缩短为止。

(6)当所有关键工作的持续时间都已达到其能缩短的极限而工期仍不能满足要求时，则应对计划的原技术、组织方案进行调整，或对要求工期重新审定。

2.选择压缩作业时间的关键工作应考虑的因素

(1)备用资源充足。

(2)压缩作业时间对质量和安全影响较小。

(3)压缩作业时间所需增加的费用最少。

(二)费用优化

1.费用优化涉及的相关概念

(1)工程的工期-成本曲线。工程成本是由直接费用和间接费用所组成的。

一般来说，工程的间接费用与施工工期成正比，间接费用随着工期的增加而递增。间接费用包括管理人员、领导人员、技术人员、后勤人员的工资；全工地性设施的租赁费；现场一切临时设施；公用和福利事业费；利息等。

工程的直接费用，一般来说，它是随着工期缩短而递增。如工程采取缩短工期的措施，往往会增加工程成本。例如增加工人数量、增加工作班次、增加施工机械和设备的数量及更换大功率的施工机械、采取更有效的施工方法等，以上这些措施，都会增加工程成本。

在正常工期T0和加快工期TS之间，缩短工期将引起直接费用的增加和间接费用的减少；反之，拉长工期会使直接费用减少，间接费用增加。工程总成本是直接费用和间接费用之和，是上述两曲线的组合。工期-成本曲线，如图4-21所示。

费用优化的目的：①寻求直接费用与间接费用总和即成本最低的最优工期TB，以及与此相适应的网络计划中各工作的进度安排；②在工期规定(T1)的条件下，寻求与此相对应的最低成本，以及网络计划中各工作的进度安排。

(2)工作的持续时间-费用曲线。如图4-22所示，这一曲线反映网络计划中的各项工作占用不同的持续时间时，相应的直接费用也不一样。在正常持续时间D的条件下，所需要的直接费用为M；当持续时间缩短为d(加快持续时间)时，相应的直接费用为m。

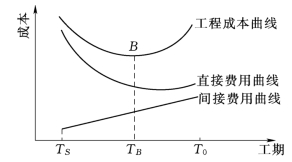
图4-21　工期-成本曲线

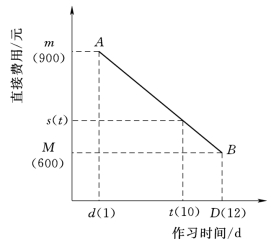
图4-22　工作的持续时间-费用曲线

为了简化起见，通常可用直线AB表示工作持续时间与费用的关系。工作持续时间t介于D和d之间时：

1)工程成本(工程总费用)是由直接费用和间接费用所组成的，若令工程成本符号为S，直接费用符号为C，间接费用符号为F，则有：S=C+F。

2)令任意一项工作的直接费用变化率为ΔCi—j，其反映该项工作缩短(或延长)单位持续时间所需增加(或减少)的直接费用数额。参照“工作的持续时间-费用曲线”，即：

图4-21中：

ΔCi—j=(900-600)÷(12-7)=60(元/d)

3)工程的间接费用一般是根据取费标准、费用定额和工作时间由工程预算确定的。通常工程总工期越长，工程的总间接费用就越大，反之就越小，二者成正比关系，这样，单位时间内间接费用的变化也是固定的，令间接费用变化率为ΔKi—j，则有：

式中 F1、T1——正常作业时间对应的总间接费用和总工期；

F2、T2——网络优化后对应的总间接费用和总工期；

ΔKi—j——间接费用变化率。

在整个工程计划中，间接费用变化率ΔKi—j为一个常数。

2.费用优化的方法

网络计划费用优化的基本方法有两种：一种是以正常时间计划方案为基础，采用压缩工期的方法调整和优化网络计划；另一种是以极限时间的计划方案为基础，采用延长工期的方法调整和优化网络计划。第一种方法在工程中应用较为广泛，下面进行详细介绍。

以正常时间计划方案为基础，采用压缩工期的方法寻求最优方案时，必须遵循以下几条基本规则。

(1)必须压缩关键工序，缩短关键线路，否则达不到缩短工程工期的目的。

(2)只能压缩有可能被压缩的工序，即正常时间大于极限时间的关键工序。

(3)压缩关键线路上直接费用变化率ΔCi—j小于间接费用变化率ΔKi—j的工序，这样既可以缩短工期，又可以使总费用减少。

(4)关键工序压缩的时间要受到以下两个条件的限制：①受压缩后工序的持续时间不得小于极限时间；②压缩后不得由关键工序变为非关键工序。也就是说，压缩是在保持仍为关键线路的条件下进行的。如果原来只有一条关键线路，则最多只能压缩此线路上某工序到刚出现另一条或数条新关键线路为止。否则，总工期不能因工序压缩而缩短。

(5)如果有几条关键线路，就要在这几条关键线路上同时压缩相同的时间，缩短时间为这几条关键线路上可以压缩时间的最小值。

在调整优化时，要抓住关键线路，逐次压缩此线路上直接费用变化率小于间接费用变化率的关键工序，压缩时间以上述两个条件为准则，能压缩多少就压缩多少，直至不能压缩为止。此时的计划方案就是最优方案。这样调整，既可以使总工期缩短，又可以使总费用不增加或者减少。

【例4-5】 已知某工程双代号网络计划，如图4-23所示，图中箭线下方括号外数字为工作的正常时间，括号内数字为最短持续时间；箭线上方括号外数字，为工作按正常持续时间完成时所需的直接费用，括号内数字为工作按最短持续时间完成时所需的直接费用。该工程的间接费用率为0.8万元/d，试对其进行费用优化。

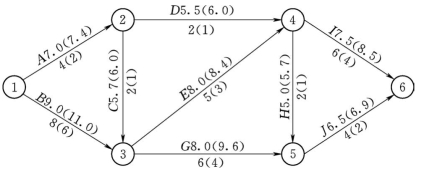
图4-23　初始网络计划

【解】：

(1)根据各项工作的正常持续时间，用标号法(所谓标号法，就是对网络图中的节点赋予两个编号，第一个标号表示从起点到该点的最短路长度，第二个标号表示在从起点到该点的最短路上，该点前面一个节点的编号，从而找到起点至终点的最短路线及距离。)确定网络计划的计算工期和关键线路，如图4-24所示。计算工期为19d，关键线路有两条，即：①—③—④—⑥和①—③—④—⑤—⑥。

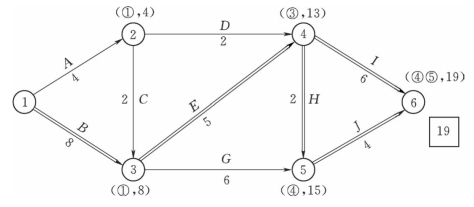(www.daowen.com)

图4-24　初始网络计划中的关键线路

(2)计算各项工作的直接费用率。

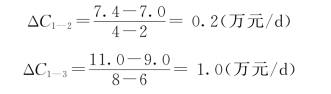
ΔC2—3=0.3(万元/d)

ΔC2—4=0.5(万元/d)

ΔC3—4=0.2(万元/d)

ΔC3—5=0.8(万元/d)

ΔC4—5=0.7(万元/d)

ΔC4—6=0.5(万元/d)

ΔC5—6=0.2(万元/d)

(3)计算工程总费用。

1)直接费总和：C=7.0+9.0+5.7+5.5+8.0+8.0+5.0+7.5+6.5=62.2(万元)；

2)间接费总和：F=0.8×19=15.2(万元)；

3)工程总费用：S=C+F=62.2+15.2=77.4(万元)。

(4)通过压缩关键工作的持续时间进行费用优化，优化过程见表4-7。

表4-7　优化表

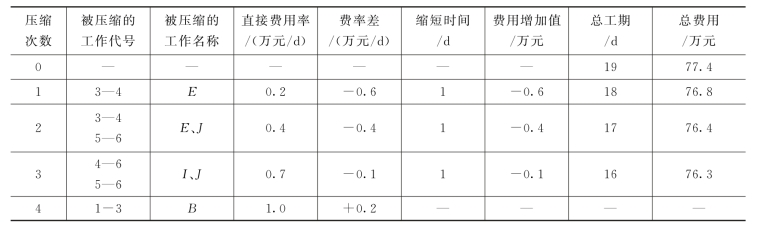
1)第一次压缩。从图4-24可知，该网络计划中有两条关键线路，为了同时缩短两条关键线路的总持续，有以下4个压缩方案。

a.压缩工作B，直接费用率为1.0万元/d。

b.压缩工作E，直接费用率为0.2万元/d。

c.同时压缩工作H和工作I，组合直接费用率为：0.7+0.5=1.2(万元/d)。

d.同时压缩工作I和工作J，组合直接费用率为：0.5+0.2=0.7(万元/d)。

在上述压缩方案中，由于工作E的直接费用率最小，故应选择工作E为压缩对象。工作E的直接费用率0.2万元/d，小于间接费用率0.8万元/d，说明压缩工作E可使工程总费用降低。将工作E的持续时间压缩至最短持续时间3d，利用标号法重新确定计算工期和关键线路，如图4-25所示。此时，关键工作E被压缩成非关键工作，故将其持续时间延长为4d，使成为关键工作。第一次压缩后的网络计划，如图4-26所示。

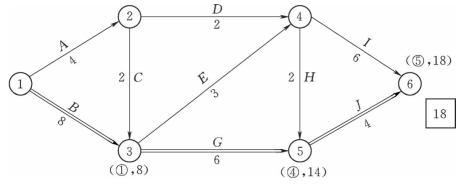
图4-25　工作E压缩至最短时的关键线路

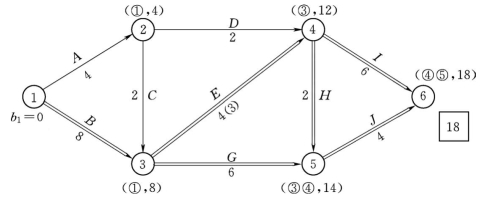
图4-26　第一次压缩后的网络计划

2)第二次压缩。从图4-25可知，该网络计划中有3条关键线路，即：①—③—④—⑥、①—③—④—⑤—⑥和①—③—⑤—⑥。为了同时缩短3条关键线路的总持续时间，有以下5个压缩方案。

a.压缩工作B，直接费用率为1.0万元/d。

b.同时压缩工作E和工作G，组合直接费用率为：0.2+0.8=1.0(万元/d)。

c.同时压缩工作E和工作J，组合直接费用率为：0.2+0.2=0.4(万元/d)。

d.同时压缩工作G、工作H和工作J，组合直接费用率为：0.8+0.7+0.5=2.0(万元/d)。

e.同时压缩工作I和工作J，组合直接费用率为：0.5+0.2=0.7(万元/d)。

在上述压缩方案中，由于工作E和工作J的组合直接费用率最小，故应选择工作E和工作J作为压缩对象。工作E和工作J的组合直接费用率0.4万元/d，小于间接费用率0.8万元/d，说明同时压缩工作E和工作J可使工程总费用降低。由于工作E的持续时间只能压缩1d，工作J的持续时间也只能随之压缩1d。工作E和工作J的持续时间同时压缩1d后，利用标号法重新确定计算工期和关键线路。此时，关键线路由压缩前的3条变为两条，即：①—③—④—⑥和①—③—⑤—⑥。原来的关键工作H未经压缩而被动地变成了非关键工作。第二次压缩后的网络计划，如图4-27所示。此时，关键工作E的持续时间已达最短，不能再压缩，故其直接费用率变为无穷大。

3)第三次压缩。从图4-26可知，由于工作E不能再压缩，而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间，只有以下3个压缩方案。

a.压缩工作B，直接费用率为1.0万元/d。

b.同时压缩工作G和工作I，组合直接费用率为：0.8+0.5=1.3(万元/d)。

c.同时压缩工作I和工作J，组合直接费用率为：0.5+0.2=0.7(万元/d)。

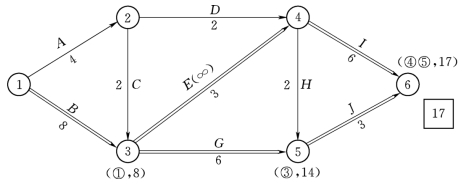
图4-27　第二次压缩后的网络计划

在上述压缩方案中，由于工作I和工作J的组合直接费用率最小，故应选择工作I和工作J作为压缩对象。工作I和工作J的组合直接费用率0.7万元/d，小于间接费用率0.8万元/d，说明同时压缩工作I和工作J可使工程总费用降低。由于工作J的持续时间只能压缩1d，工作I的持续时间也只能随之压缩1d。工作I和工作J的持续时间同时压缩1d后，利用标号法重新确定计算工期和关键线路。此时，关键线路仍然为两条，即：①—③—④—⑥和①—③—⑤—⑥。第三次压缩后的网络计划，如图4-28所示。此时，关键工作I的持续时间也已达最短，不能再压缩，故其直接费用率变为无穷大。

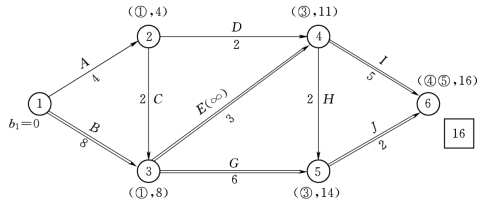
图4-28　第三次压缩后的网络计划

4)第四次压缩。从图4-28可知，由于工作E和工作I不能再压缩，而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间，只有以下两个压缩方案。

a.压缩工作B，直接费用率为1.0万元/d。

b.同时压缩工作G和工作I，组合直接费用率为0.8+0.5=1.3(万元/d)。

在上述压缩方案中，由于工作B的直接费用率最小，故应选择工作B作为压缩对象。但是，由于工作B的直接费用率1.0万元/d，大于间接费用率0.8万元/d，说明压缩工作B会使工程总费用增加。因此，不需要压缩工作B，优化方案已得到，费用优化后的网络计划，如图4-29所示。图中箭线上方括号内数字为工作的直接费。

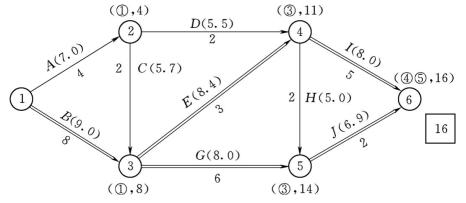
图4-29　费用优化后的网络计划

(5)计算优化后的工程总费用。

1)直接费总和：C=7.0+9.0+5.7+5.5+8.4+8.0+5.0+8.0+6.9=63.5(万元)。

2)间接费总和：F=0.8×16=12.8(万元)。

3)工程总费用：S=C+F=63.5+12.8=76.3(万元)。