为了动态地优化、调整执行过程当中的工程项目进度计划，必须对经过图形绘制步骤而形成的网络计划实施各种时间参数计算。所谓时间参数，是指网络计划、工作及节点所具有的各种时间值。

囿于教材篇幅限制，下面仅将工程项目管理实践中常用到的双代号网络计划相关时间参数的计算加以介绍。

(一)双代号网络计划时间参数简介

双代号网络计划中的肯定型网络计划涉及以下时间参数，见表4-6。

表4-6　双代号网络时间参数

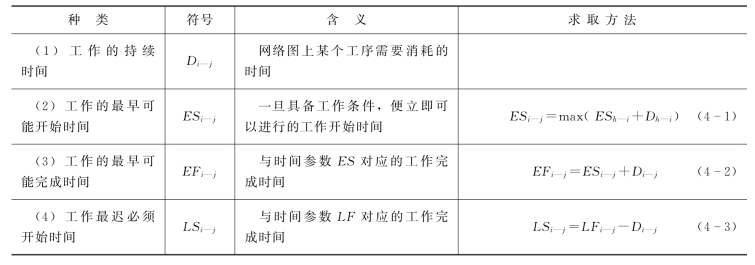
续表

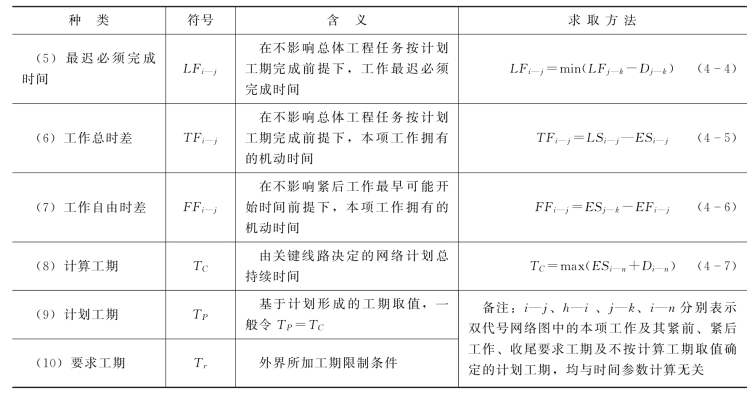
(二)双代号网络计划时间参数计算

1.计算网络时间参数的步骤

(1)从网络图的起点节点开始，顺着箭线方向依次计算各项工作的最早可能开始时间和最早可能完成时间。整个计算过程是加法过程。

(2)确定工程的总工期。

(3)从网络图的终点节点开始，逆着箭线方向依次计算各项工作的最迟必须完成时间和最迟必须开始时间。整个计算过程是个减法过程。

(4)计算各项工作的总时差和自由时差。

(5)确定关键线路及关键工作。

2.网络时间参数的图上计算法

网络时间参数的计算方法有图上计算法、表上计算法、矩阵法等，图上计算法直观又简便，下面通过例题来认识其具体做法。

【例4-4】 计算下图所示双代号网络计划的时间参数。

【解】：

(1)计算方法和步骤。

工作的最早可能开始时间应从网络图的起点节点开始的工作算起，顺着箭线方向依次逐项计算，直到以终点节点为结束节点的工作计算完成为止。必须先计算其紧前工作，然后才能计算本工作。

图4-17中，以起点节点①为箭尾节点的工作1—2，因为未规定其最早可能开始时间，一般其值取为零，即：

ES(1—2)=0

其他工作i—j的最早开始时间按式(4-1)进行计算：

ES(2—3)=max{ES(1—2)+D(1—2)}=0+2=2

ES(2—4)=max{ES(1—2)+D(1—2)}=0+2=2

ES(3—7)=max{ES(2—3)+D(2—3)}=2+2=4

ES(5—6)=max{ES(2—3)+D(2—3)，ES(2—4)+D(2—4)}=max{2+2，2+3}=5

ES(4—8)=max{ES(2—4)+D(2-4)}=2+3=5

ES(8—9)=max{ES(5—6)+D(5—6)，ES(4—8)+D(4—8)}=max{5+3，5+1}=8

ES(7—9)=max{ES(5—6)+D(5—6)，ES(3—7)+D(3—7)}=max{5+3，4+2}=8

ES(9—10)=max{ES(7—9)+D(7—9)，ES(8—9)+D(8—9)}=max{8+3，8+1}=11

(2)计算各工作的最早可能完成时间。

工作i—j的最早可能完成时间EFi—j的计算按式(4-2)进行，因此得到：

ES(1—2)=ES(1—2)+D(1—2)=0+2=2

EF(2—3)=ES(2—3)+D(2—3)=2+2=4

EF(2—4)=ES(2—4)+D(2—4)=2+3=5

EF(3—7)=ES(3—7)+D(3—7)=4+2=6

EF(5—6)=ES(5—6)+D(5—6)=5+3=8

EF(4—8)=ES(4—8)+D(4—8)=5+1=6

EF(7—9)=ES(7—9)+D(7—9)=8+3=11

EF(8—9)=ES(8—9)+D(8—9)=8+1=9(www.daowen.com)

EF(9—10)=ES(9—10)+D(9—10)=11+1=12

(3)计算网络计划的总工期。

网络计划的计算工期TC的计算按式(4-7)进行，因此得到：

TC=max{EF(9—10)}=12

(4)网络计划的计划工期。

由于未规定要求工期，所以该网络计划的计划工期(TP)可按其计算工期确定，即：

TP=TC=12

(5)工作的最迟必须完成时间的计算。

工作最迟必须完成时间应从网络图的终点节点开始，逆着箭线的方向，自右至左进行计算，直到以起点节点为开始节点的工作计算完成为止。必须先计算紧后工作，然后才能计算本工作。以终点节点为箭头节点的工作最迟必须完成时间应等于TP，即：

LFi—n=TP

因此得到：

LF9—10=12

其他工作i—j的最迟完成时间是其诸紧后工作最迟必须开始时间的最小值，故应按式(4-4)进行计算。因此得到：

LF(7—9)=min{LF(9—10)-D(9—10)}=12-1=11

LF(8—9)=min{LF(9—10)-D(9—10)}=12-1=11

LF(3—7)=min{LF(7—9)-D(7—9)}=11-3=8

LF(5—6)=min{LF(7—9)-D(7—9)，LF(8—9)-D(8—9)}=min{11-3，11-1}=8

LF(4—8)=min{LF(8—9)-D(8—9)}=11-1=10

LF(2—4)=min{LF(5—6)-D(5—6)，LF(4—8)-D(4—8)}=min{8-3，10-1}=5

LF(2—3)=min{LF(3—7)-D(3—7)，LF(5—6)-D(5—6)}=min{8-2，8-3}=5

LF(1—2)=min{LF(2—3)-D(2—3)，LF(2—4)-D(2—4)}=min{5-2，5-3}=2

(6)工作最迟必须开始时间的计算。

工作i—j的最迟必须开始时间是其最迟必须完成时间与其持续时间之差，可按式(4-3)计算(计算过程略)。因此得到图4-17中各项工作的最迟必须开始时间，列入图4-18内。

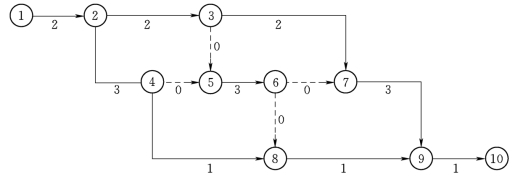
图4-17 网络时间参数计算

(7)工作总时差的计算。

一项工作的机动范围要受其紧前工作和紧后工作的约束。它的极限机动时间是从其最早可能开始时间到最迟必须完成时间这个时间段，从中扣除本身作业必须占用的时间之后，其余时间才可机动使用，因此：

TFi—j=LFi—j-ESi—j-Di—j=LFi—j-EFi—j=LSi—j—ESi—j

由此便可计算出各个工作的总时差：

TF(1—2)=0-0=2-2=0

TF(2—3)=3-2=5-4=1

TF(2—4)=2-2=5-5=0

…

(8)工作自由时差的计算。

根据自由时差的定义，其值应等于其紧后工作最早可能开始时间与本工作最早可能完成时间之差，故按式(4-6)计算。因此得到：

FFi—j=ESj—k-EFi—j

FF(1—2)=2-2=0

FF(2—3)=4-4=0

FF(2—4)=5-5=0

…

本例双代号网络计划时间参数的计算结果，如图4-18所示。