【学习目标】

1）了解液压传动静力学和动力学的基本知识。

2）了解液压传动常用力学应用实例。

【任务描述】

了解液压传动的力学知识。

【知识准备】

一、液压传动的静力学基础

流体：液体和气体。

特点：液体看作是不可压缩的，气体则是可压缩的，气体的压缩性大约是液体的10000倍。

1.液体静压力p

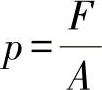
式中 p——流体静压力（Pa）；

A——作用的面积（m²）；

F——作用的面积上所受的法向力（N）。

绝对压力：以零压力为基准的压力。

相对压力：以大气压力为基准的压力，也称表压力。

绝对压力与相对压力的关系为

相对压力=绝对压力-大气压力

2.压力的度量标准

1Pa=1N/m²

1MPa=10⁶Pa

1bar=1.02kgf/cm²=0.1MPa

3.帕斯卡原理

定义：在密闭容器内，施加于静止液体上的压力将以等值同时传到液体各点，又称静压传递原理。

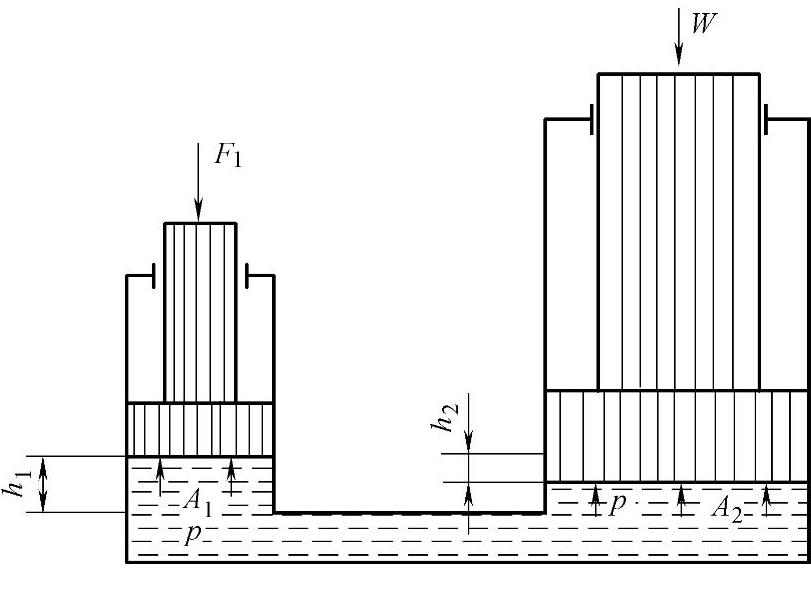
图1-2 液压千斤顶的简化模型

液压千斤顶是帕斯卡原理应用的典型实例。图1-2所示为液压千斤顶的简化模型。

公式 ，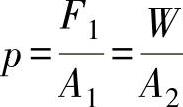

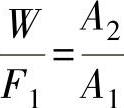
结论：工作压力取决于负载，而与流入的流体多少无关。

二、液压传动的动力学

1.基本概念

（1）理想液体既不可压缩又无黏性的液体。

（2）理想气体可压缩但没有黏性的气体。

（3）流量和平均流速

1）流量q：单位时间内流过某过流截面的流体的体积，即

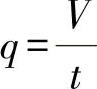
式中 V——过流截面的体积（m³）；

t——所用的时间（s）；

q——流量（m³/s）。

2）平均流速v：流体质点在单位时间内流过的距离，即

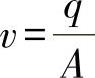
式中 v——流体的平均流速（m/s）；

q——管道中流体的流量（m³/s）；

A——管道过流截面积（m²）。

结论：活塞的运动速度v取决于进入液压缸的流量q，而与流体压力p的大小无关。(www.daowen.com)

2.连续性方程

根据质量守恒定律，单位时间内流过任意管道的截面的流体质量为常数c，即

ρ^Av=c

式中 ρ——流体的密度；

A——管道的过流截面积；

v——流体的平均流速。

（1）气体流动的连续性方程气体的密度ρ受温度和压力的变化较大，又因气体是可压缩的，故在不同的截面上气体密度不同。连续性方程为

ρ₁A₁V₁=ρ₂A₂V₂

（2）液体流动的连续性方程因液体密度ρ受温度和压力的变化较小，可认为液体是不可压缩的。则有

A_v=q=常数

或 A₁v₁=A₂v₂=q

图1-3所示为液压千斤顶的压油过程。从连续性方程可得出，它的流速与过流截面积成反比，流过过流截面A₁的液体流量等于流过过流截面A₂的流量。

结论：管径大的地方流速慢，管径小的地方流速快。

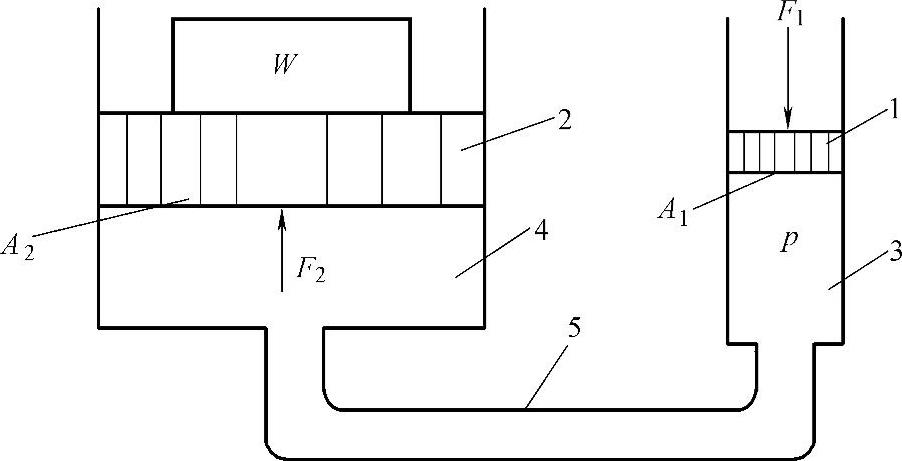
图1-3 液压千斤顶的压油过程

1、2—活塞 3、4—油腔 5—油管

【任务实施】

一、工具准备

笔、稿纸、计算器等。

二、实施步骤

【例1-1】图1-3所示液压千斤顶中，已知活塞的有效作用面积A₁=1.13×10^-4m²，A₂=9.62×10^-4m²，施加在小活塞上的力F₁=5.78×10³N。问千斤顶能顶起多重的物体？

解：小活塞所在的液压缸内的压力p₁为

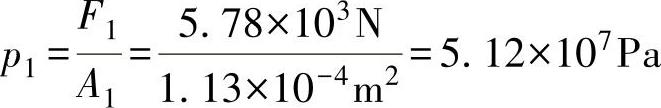
根据帕斯卡原理，作用在大、小活塞上的压力相等，即p₁=p₂，则W为

W=p₂A₂=p₁A₂

=5.12×10⁷Pa×9.62×10^-4m²

=4.92×10⁴N

因此液压千斤顶能顶起4.92×10⁴N的重物。作用力放大了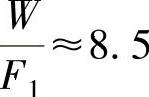倍。

【例1-2】图1-3所示液压千斤顶中，已知活塞1的有效作用面积A₁=1.13×10^-4m²，活塞2的有效作用面积A₂=9.62×10^-4m²，油管5的截面积A₅=1.3×10^-5m²。假定活塞1的下压速度v₁=0.2m/s。试求活塞2的上升速度v₂和油管5内液体的平均速度v₅。

解：1）活塞1所排的流量q₁为

q₁=A₁v₁=1.13×10^-4m²×0.2m/s=2.26×10^-5m³/s

2）根据连续性方程，活塞2所排的流量q₂=q₁，得

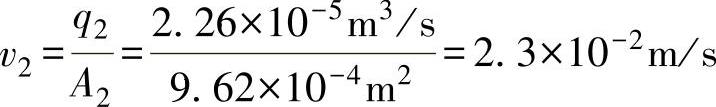
3）同理，油管5中的流量q₅=q₂=q₁，得

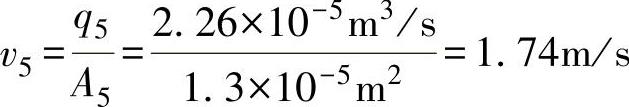
三、任务组织

1）根据授课班级人数完成学生实验教学分组。

2）小组成员通过分工协作算出结果，完成实施任务。

3）每个小组派出代表展示和讲解结果。

四、任务评价

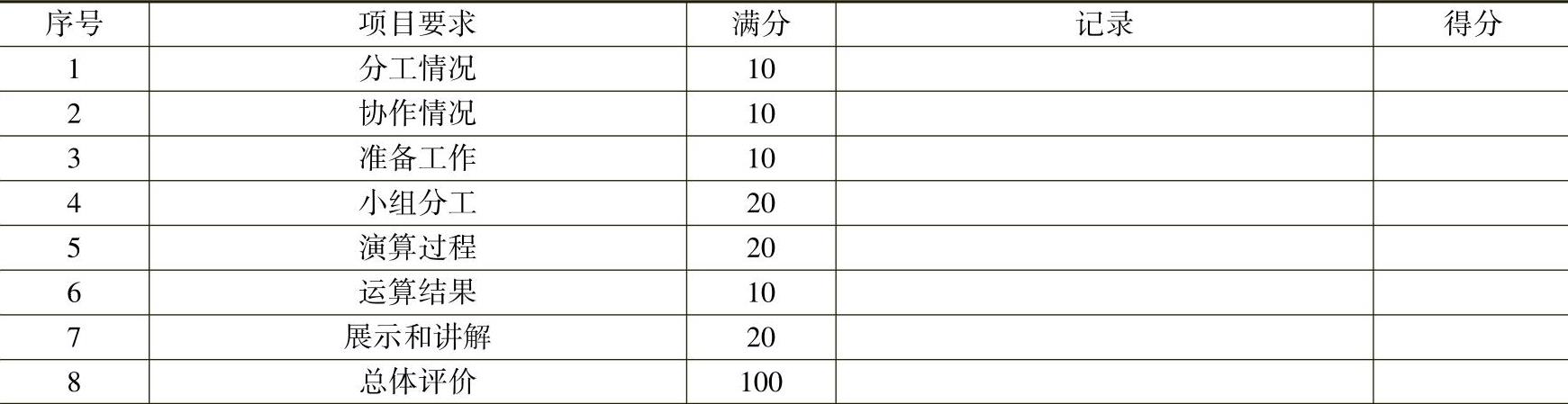
填写液压传动力学计算任务评价表（表1-1）。

表1-1 液压传动力学计算任务评价表