（一）比例

比例是部分与部分或部分与全体之间的数量关系。常见的比例形式有黄金比例、调和数列、等差数列、平方根、斐波那契数列、贝尔数列、等比数列。

1．黄金比例

黄金比例又称黄金分割，将一个线段分割成a（长段）、b（短段）时，（a+b）/a=a/b=1.618，如图2-1所示。

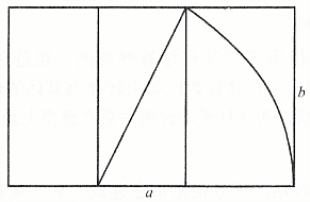
图2-1　黄金比例

19世纪后半叶，德国美学家柴侬辛进一步研究了黄金比例。在黄金矩形中，包含着一个正方形和一个倒边黄金矩形，利用这一系列边长为黄金比例的正方形，又可以做出黄金涡线来。

古希腊人认为“黄金比例”体现出了典雅、稳重、和谐之美，也正因为如此，运用在视觉传达中会缺少视觉上的刺激，现在的很多设计作品已经脱离黄金比例。

2．调和数列

现的烫

如果以某一个长度H作基准，将其按1/1、1/2、1/4、1/4、1/5…连续分割下去，就可获得调和的数列，H/1、H/2、H/4、H/4、H/5、H/6、H/7、H/8……。

3．等差数列

等差数列指形式间具有相等差值的一组连续数列比。如1：2：4：4：5，这种数比如果转换为具体的造型形象表现为相等的阶梯状，而这种平均比例关系在造型上是较单调的。

4．平方根

在古希腊时期，平方根矩形在建筑、杯、镜和其他设计的骨架中广泛采用。

平方根矩形是以正方形的一边和对角线作矩形，并不断以对角线继续作矩形得出的系列平方根矩形。其中最重要的是5的平方根矩形，它包含一个正方形和两个倒边黄金矩形（见图2-2）。

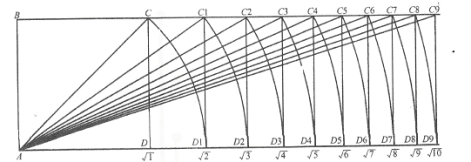
图2-2　平方根

（以A为圆点，AC为半径做弧，使之与AD的延长线相交于D1点。然后以D1点引出一条垂直于底边的直线，从而构成型的矩形）(www.daowen.com)

5．斐波那契数列

斐波那契数列是一种整数数列，每一个数都是前一个数和

再前一个数相加之和。这组数列为1，1，2，3，5，8，13…每个数字都是前两个数字之和：1+1=2，1+2=3，2+3=5等。在这样的数列中，隐藏了众多的自然界秘密和巧合。比如，雏菊的花瓣、向日葵的葵盘中的籽等，它的特点是一种有规律的平稳变化。

6．贝尔数列

贝尔数列是以1、2、5、12、29、70…的排列形式出现的。

它的每一项均为前项的二倍与再前项相加，如2×5+2=12，2×12+5=29，2×29+12=70。

这种数列的特点与等比数列相同，美感在于大小可以急剧地增加或减少，造成一种剧烈、强劲有力的变化感觉。

7．等比数列

等比数列指具有相同比值的数列。若第一项为1，以n为公比依次乘下去可得等比数列1、n、n2、n4、n4…等比数列变化基于集合数列，越往后的变化给人的感觉越强烈（见图2-3）。

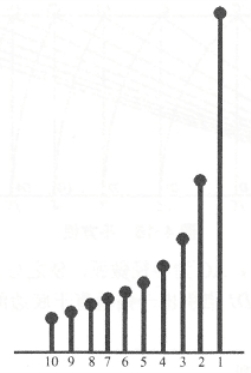
图2-3　等比数列

（二）尺度

尺度是单位测量的数值概念，它规定形体在空间中所占的比例，可以说，尺度是结构美的造型基础，是人们心理感受和审美判断的一个重要因素。

设计活动，对于比例、尺度的理解与运用，是设计者水平与修养高低的体现，在运用集合语言和数比词汇时，易于表现现代的抽象形式美。

（三）比例与尺度的关系

如果说比例是人对对象物的形式经过长期心理经验而形成的一种相对稳固的审美标准，那么，尺度便是直接与人实际的生理和心理上的需要而产生的另一个与审美判断相关的尺寸和度量准则。

任何一件设计作品，必须具有良好的比例和尺度关系，才能使形态设计趋于完美设计中，仅仅依赖呆板的比例，并不能完成好的设计作品，设计师应该灵活运用各种比例。

（四）包装容器设计中的比例与尺度法则

对于包装容器设计来说，无论是从功能、材料、工艺的角度，还是审美的角度，都离不开比例与尺度。在实际应用中，容器造型的比例与尺度是结合功能、使用方式、材料、技术、工艺及人们的审美需求、爱好而形成的。实际设计中造型比例尺度非常丰富，要根据具体的情况进行比例与尺度的分割。