为分析围堰结构的安全性，对堰体和混凝土防渗墙进行应力、变形的平面有限元计算。具体计算分述如下。

（一）计算条件及计算模型

1.计算条件

根据2006年6月16日四川省院召开的会议研究，确定采用如下的计算条件。

（1）选择下坝2为计算剖面，采用平面非线性有限元分析计算。

（2）对塑性混凝土、围堰填筑体、地基覆盖层采用邓肯·张E—B模型、岩基采用线弹性模型。

（3）塑性混凝土防渗墙两侧考虑泥皮作用，墙底不考虑沉渣影响。

（4）根据施工过程模拟分析老墙及堰体不同开挖高程的应力、变形，分析评价其安全性态。

（5）在老墙条件下，基坑开挖至高程388m后，基坑充水施工新增塑性混凝土防渗墙（本文称新墙），根据施工过程模拟分析新墙及堰体不同开挖高程的应力、变形，分析评价其安全性态。

（6）新墙计算时不考虑老墙的防渗作用。

（7）对新墙采用墙体不同模量数K和泥皮接触面不同切向劲度系数K1进行敏感性分析。

2.计算断面

根据上述计算条件，选取纵向围堰推荐坝轴线剖面为有限元计算断面，其剖面如图7-56所示。为反映边界对计算结果的影响，计算范围铅直向下取至高程327m，水平方向以原塑性混凝土防渗墙中心线为基础，迎水侧范围取78.35m，基坑侧范围取171.65m。计算坐标系以断面左下角为坐标原点，X轴向右为正，Y轴向上为正。

3.网格划分

有限元计算的网格划分如图7-57所示，整个计算网格按照计算断面的岩性特征进行离散，除了边角与不同岩层交界面上采用少数三角形单元外，其余大部分都采用四边形单元。同时对新老两道混凝土防渗墙进行了网格细化，具体有限元网格划分情况见表7-42所示。

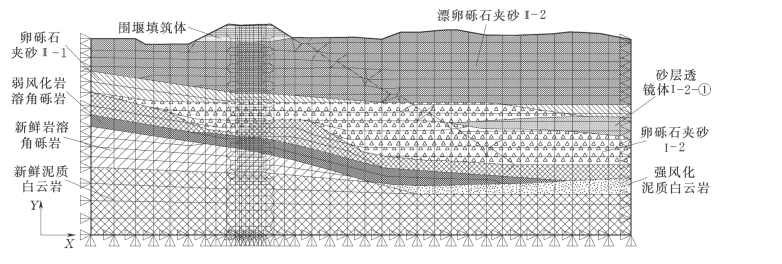
图7-57　围堰断面有限元计算网格图

表7-42　有限元网格划分情况表

4.计算方案

双墙（新墙与老墙同时存在）情况下计算方案：

当新墙和老墙同时存在时，为了研究新增塑性混凝土防渗墙弹性模量数K和泥皮接触面切向刚度系数K1对围堰和墙体应力变形的影响，考虑按表7-43中所示的方案组合进行敏感性分析。

表7-43　双墙计算方案表

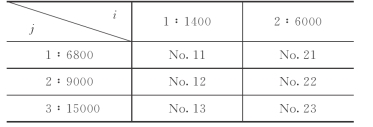
注　1.第i类方案表示泥皮接触面切向劲度系数K1取不同值。
2.第j类方案表示新增塑性混凝土防渗墙弹性模量数K取不同值。
3.各组合方案中，原塑性混凝土防渗墙的弹性模量数K保持6800不变。

5.材料参数

根据四川省水利水电勘测设计研究提供的各种岩层及围堰填筑体物理力学参数确定邓肯·张E—B模型参数如表7-44所示。

（二）计算模型及计算程序

（1）本实例主要采用大坝及基础工程结构分析通用程序软件包GPDFA2005进行计算，该程序是依邓肯·张的E—B模型编写的。该程序曾对三峡二期低双塑性混凝土防渗墙、山西册田水库土坝防渗墙、山西横泉水库水坝防渗墙和黄壁庄水库副坝防渗墙等工程进行过非线性有限元计算分析，取得了很好的结果。

（2）基坑开挖加载方法。本次计算中，为模拟基坑土体的开挖过程，采用改进的Mana法来进行开挖释放荷载的模拟计算。

具体对第i级开挖来讲，计算过程分以下几步：

（1）首先明确第i级需要挖去的土体单元即开挖域的范围，从而确定本级的开挖边界。

（2）然后根据开挖域内第i-1级的应力场计算得到第i级开挖等效释放荷载，具体由下式计算所得：

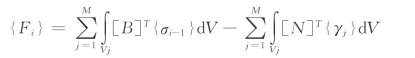
式中｛Fi｝——第i级开挖等效释放荷载；

M——第i级开挖域内被挖去的单元总数；

｛σi-1｝——第i-1级开挖得到的应力场；

｛γj｝——第i级开挖域内各单元的体积力；

［B］——应变矩阵；

［N］——插值函数矩阵；

Vj——第i级开挖域内单元的体积。

（3）将第i级开挖面上的等效释放荷载，作为等效节点荷载加在剩余土体上；将第i级非开挖面上的等效释放荷载置零。

（4）将第i级开挖域内的单元置空，使其刚度很小。

（5）计算由第i级开挖等效释放荷载引起的增量位移场｛∆ui｝和增量应力场｛Δσi｝。

（6）叠加得到第i级开挖后的总位移场｛ui｝和总应力场｛σi｝。

其中

表7-44　沙湾水电站厂房基坑围堰有限元计算材料参数总表

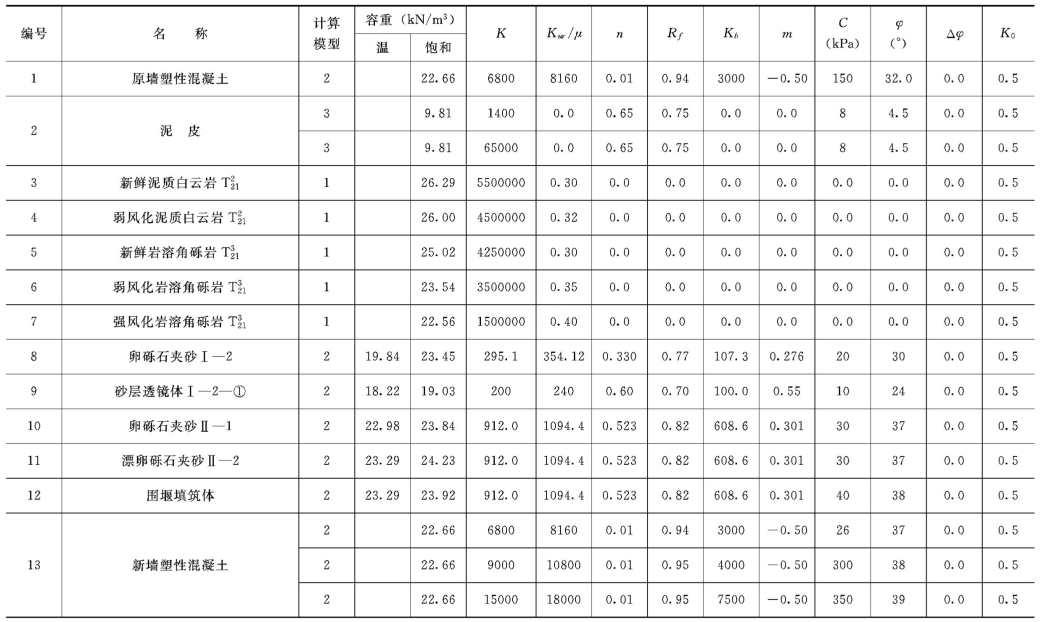
注1.表中“计算模型”一栏所填数字中1表示线弹性模型，2表示邓肯·张E—B模型，3表示接触面滑动模型。
2.岩石容重采用干容重。
3.接触面滑动模型容重取水的容重。

（三）分期加载过程

根据四川省水利水电勘测设计研究院的要求，采用如下的分期加载过程来模拟整个施工过程。

根据新墙与老墙壁同时存在的双墙条件，采用如下的加载过程：

（1）计算天然堰基应力，将堰基中的变形与位移置0。

（2）原河床上填筑砂卵石围堰，堰顶高程425.32m。

（3）原塑性混凝土防渗墙施工，墙底高程355.10m，基坑水位417.0m。

（4）基坑依次抽水、开挖至高程408m、高程400m、高程392m、高程388m。

（5）基坑充水至417m水位。

（6）新增塑性混凝土防渗墙施工，墙底高程355.10m，基坑水位417m。

（7）基坑抽水至388m水位。

（8）基坑依次抽水、开挖至高程384m、高程376m、高程368m、高程360m。

需要说明的是，按四川省院的建议，由于未计算基坑水位高程417m工况，故高程417m的堰体渗透压力等值线，参照高程408m的堰体渗压力等值线进行计算。

（四）计算成果分析与研究

1.方案开挖至基面360m时堰体及墙体工作性态研究

（1）堰体应力变形分析。根据新增塑性混凝土防渗墙弹性模量数K和泥皮接触面切向刚度系数K1取不同组合值的敏感性分的，将堰体的应力、变形和应力水平等值线图绘出。由于各方案等值线相近似，本书仅给出方案No.13的等值线图（见图7-58）。从计算结果可以看出，各种方案下，堰体的应力和变形，其数值和分布规律非常接近。

由图7-58可知：堰体及堰基应力随深度增加而增加，在计算范围内，最大大主应力约为2.1MPa，最大小主应力约为0.9MPa，最小小主应力约为-0.38～-0.36MPa，发生在高程370～377m范围的新墙上游侧。另外，由于基坑开挖引起应力释放，故开挖边坡附近的土体存在受拉趋势，在高程388～395m范围开挖边坡附近的土体中，存在最大-0.25MPa左右的拉应力。

堰体的应力水平呈现以下特征。基岩中的应力水平都较低，约为0.5左右；而上部覆盖层中存在两个应力水平较高的集中区（应力水平大于0.9），一个位于新混凝土防渗墙上游侧的卵砾石夹砂Ⅱ—1层和漂卵砾厂夹砂Ⅱ—2层中，高程范围为387～407m，由于该区域位于堰体内部，故无大碍；另一个位于堰体下游边坡表层附近，主要集中于基坑底部至第3级马道之间，高程范围为360～405m，如图7-59所示，该区域对堰体下游边坡的稳定性有影响，建议采取相应的加固处理措施。

堰体最大沉降量约为16～18cm，发生在高程413～418m范围的新防渗墙上游侧覆盖层内；由开挖所引起的最大抬升量约为31～35cm，发生在高程385～393m范围的开挖边坡附近；最大水平位移约为38～40cm，仍然发生在高程385～393m范围的开挖边坡附近。

（2）墙体应力变形分析。基坑开挖至建基面高程360m时，防渗墙体的应力与变形沿高程的典型分布规律见图7-60～图7-65。同时，在表7-45和表7-46中列出了各方案防渗墙应力和变形分布特征值。

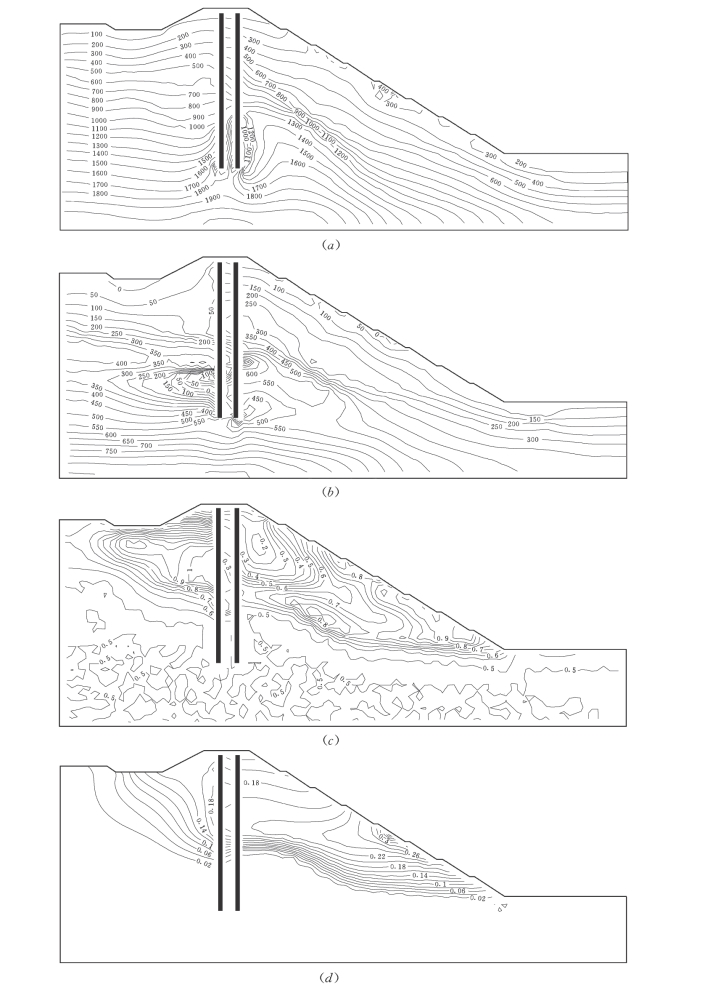
图7-58　No.13方案基坑挖至高程360m堰体应力、位移、应力水平等值线图（一）

（a）第一主应力等值线图；（b）第三主应力等值线图；（c）应力水平等值线图；（d）水平位移等值线图

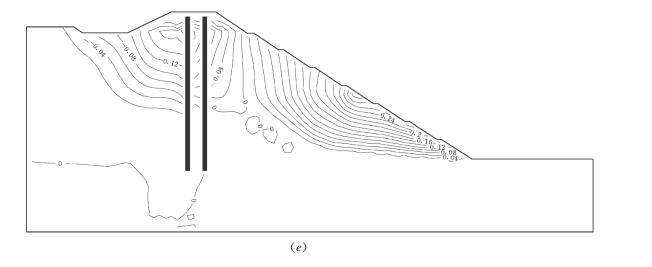
图7-58　No.13方案基坑挖至高程360m堰体应力、位移、应力水平等值线图（二）

（e）垂直位移等值线图

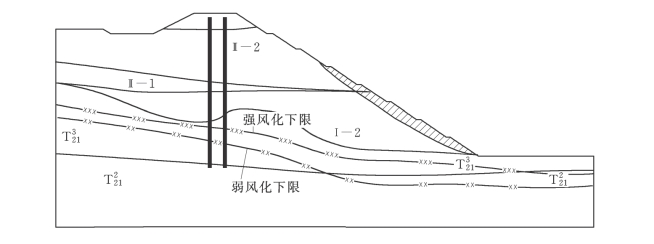
图7-59　No.13方案基坑挖至高程360m边坡应力水平达到危险水平区域图（阴影区）

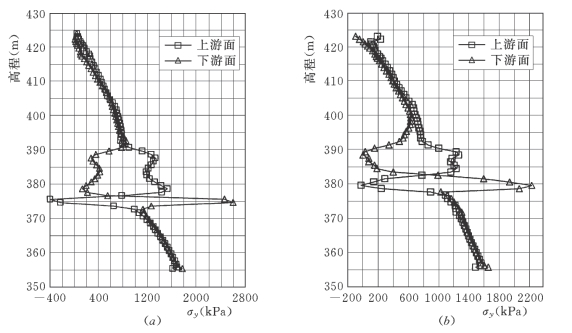
图7-60　防渗墙No.13方案σy沿高程分布曲线图

（a）新墙；（b）老墙

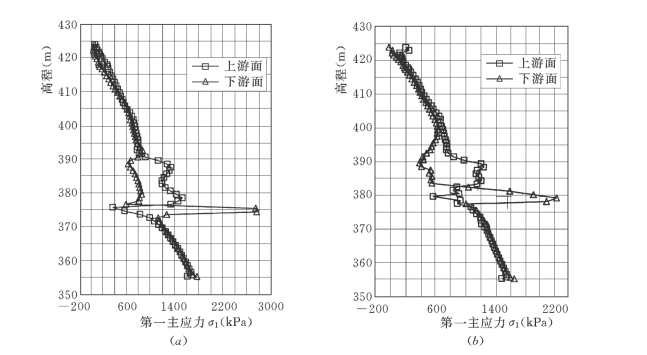
图7-61　防渗墙No.13方案第一主应力σ1沿高程分布曲线图

（a）新墙；（b）老墙

(www.daowen.com)

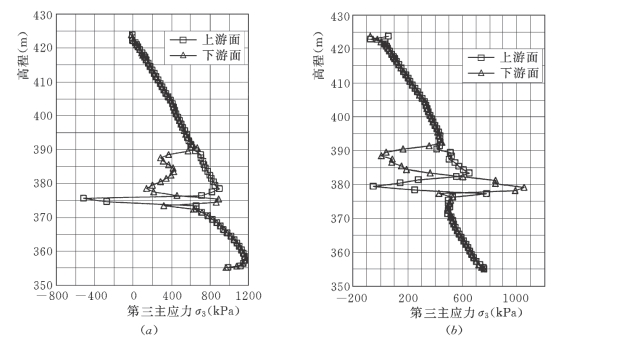
图7-62　防渗墙No.13方案第三主应力σ3沿高程分布曲线图

（a）新墙；（b）老墙

通过分析得到以下结论：

1）墙体竖向应力σy。从图7-60可以看出，新老墙墙体竖向应力σy沿墙高的分布规律基本相同。新墙在375m高程附近，老墙在380m高程附近，均因岩溶角砾与卵砾石夹砂1～2层的交界面，造成墙体应力严重集中，下游侧局部压应力增高，σy达到最大值；上游侧σy到达了最小值，部分方案出现拉应力，各方案σy特征值示于表7-45中，同时观察到，老墙的墙体顶部下游侧出现较小的拉应力。

2）墙体主应力。从图7-61～图7-62可以看出，各方案主应力沿墙高的分布规律也基本一致，大主应力σ1的分布规律与竖向应力σy基本相同。

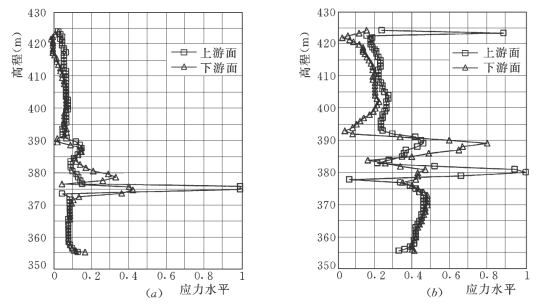
图7-63　防渗墙No.13方案应力水平沿高程分布曲线图

（a）新墙；（b）老墙

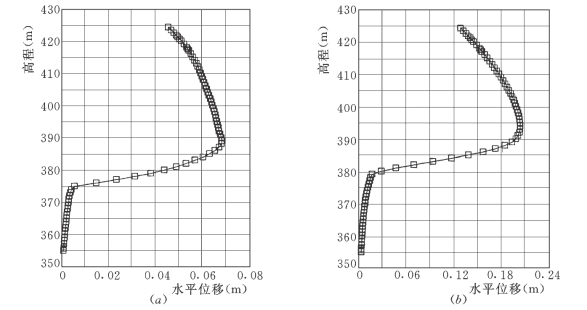
图7-64　防渗墙No.13方案水平住移沿高程分布曲线图

（a）新墙；（b）老墙

图7-65　防渗墙No.13方案垂直变位沿高程分布曲线图

（a）新墙；（b）老墙

表7-45　各方案竖向应力σy特征值（双墙方案）

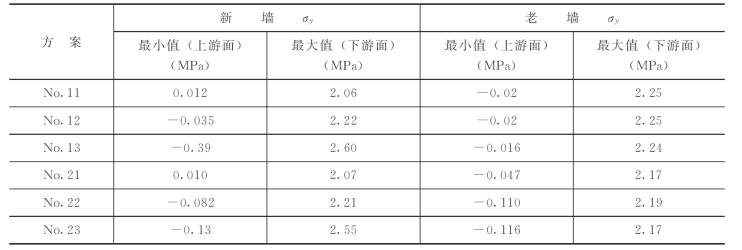
无论对于新墙还是老墙，主应力总体上都随墙体高程的增加而减小，其中，位于下部基岩、上部覆盖层与围堰填筑中的墙体，其上下游侧主应力相差不大，基本相等。而位于堰基中部卵砾石夹Ⅰ—2层中的墙体来说，其主应力沿墙高分布出现明显振荡，这主要是因为该层土体模量较低（仅295.1）所致，尤其对于岩溶角砾岩与卵岩与卵砾石夹砂Ⅰ—2层的交界面处（新墙：高程375m；老墙：高程380m），墙体应力严重集中。

对于新墙，上游侧量大σ1变化范围为1.68～1.715MPa，位于墙体底部，应力较大；最小σ3变化范围为-0.08～0.06MPa，均发生于高程375m附近，下游侧最大σ1变化范围为2.146～2.75MPa，均发生于高程375m附近；最小σ3变化范围为-0.004～0.01MPa，位于墙体顶部。

对于老墙，上游侧最大σ1变化范围为1.56～1.63MPa，位于墙体底部，最小σ3变化范围为-0.06～0.15MPa，均发生于高程380m附近。下游侧最大σ1变化范围为2.198～2.287MPa，均发生于高程380m附近，最小σ3变化范围为0.007～0.08MPa，位于墙体顶部。同时，老墙在高程389m附近，下游侧有较小的拉应力存在。

3）墙体应力水平。从图7-63可以看出，墙体的应力水平变化范围很大。

对于新墙，除位于堰基中部卵砾石夹砂Ⅰ—2层中的墙体外，其余高程墙体应力水平均小于0.2；Ⅰ—2层中墙体应力水平有所增加且分布不均，但不超过0.5；在高程375m处，墙体上游侧应力水平大于0.8，接近承载能力极限。

对于老墙，墙体应力水平总体上高于新墙，除位于堰基中部卵砾石夹砂Ⅰ—2层中的墙体外，其余高程墙体应力水平均小于0.5；Ⅰ—2层中墙体应力水平亦有所增且分布更为不均，局部下游侧达到0.8；在高程380m处，墙体上游侧应力水平均达到1.0，墙体出现剪切破坏；同时还注意到，墙体顶部上游侧应力水平增大明显。

4）墙体位移。从图7-64、图7-65和表7-46中可以看出，各方案墙体位移基本相同。

由于上部覆盖层远比下部基岩软，故新墙高程375m以上，水平位移（向下游侧）迅速增大，最大7cm（发生在高程389m附近），此处存在卵砾石夹砂Ⅰ—2层与Ⅱ—1层的交界面；老墙高程380m以上，水平位移（向下游侧）迅速增大，最大达20cm左右，发生在高程394m附近。此处存在卵砾石夹砂Ⅱ—1层与漂卵砾石夹砂Ⅱ—2层的交界面。

表7-46　各计算方案开挖至高程360m时防渗墙应力分布特征值表

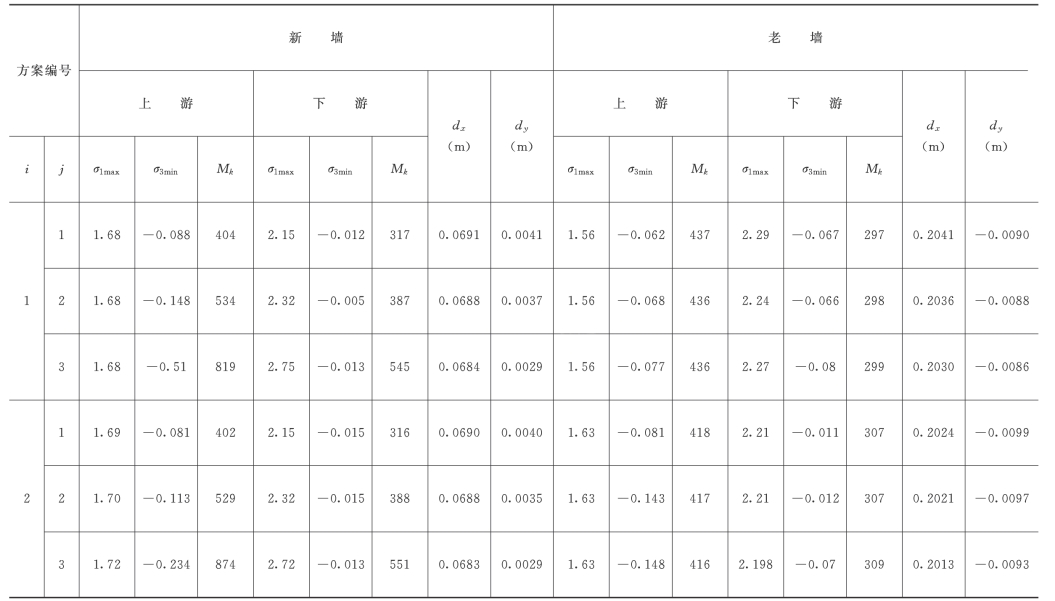
注1.表中所列σ1max和σ3min分别表示大主应力与小主应力的最大值与最小值；dx 表示墙体水平位移的最大值；dy 表示墙中垂直位移最大值，其中正值表示抬升量，负值表示沉降量。
2.应力单位为MPa。
3.Mk=K/σ1max，称为模应比。

墙体的垂直位移，基本可以忽略不计，新墙总体上呈抬升趋势，最大抬升量0.3～0.4cm，发生在高程389m附近；老墙总体上呈沉降趋势，最大沉降量0.9～1.0cm，发生在墙体顶部。

2.基坑分级开挖工程中堰体及墙体工作性态的研究

为研究基坑开挖过程对应力变形的性态，特以方案No.13为例予以讨论。基坑分级开挖过程中堰体及墙体工作性态研究。

由于本实例更多关注于新增塑性混凝土防渗墙的工作性态，从各方案开挖至360m建基面时的计算结果看，方案No.13计算所得的新墙上游侧所受拉应力最大，下游侧所受压应力最大，故将方案No.13作为最不利方案，进而分析研究该方案，基坑分级开挖过程中，堰体及墙体工作性态的变化过程。

（1）堰体应力变形分析。基坑分级开挖过程中，堰体的应力、变形和应力水平，分别示于图7-66～图7-70中。

总体上看，应力等值线值随深度的加深而增大，且基本上呈现下述特征：墙上游侧的堰体等值线接近水平分布，墙下游侧的堰体等值线与开挖边坡平行；基坑的分级开挖对堰体及基础内部的应力分布产生一定影响，同时由于新墙的修建，对墙体周围特别是墙体中下部附近的土体应力影响较大。随着基坑开挖深度的增加，墙体中下部特别是底部附近堰体的应力增大，应力集中程度有所增加，且新墙修建后，在新墙上游侧高程370～377m范围内会出现大于-0.3MPa的拉应力，且随着开挖深度的增加，该区域拉应力有所增大，当挖至建基面高程360m时，最大拉应力最终会达到-0.39MPa左右。同时，同于基坑开挖引起应力释放，开挖边坡附近的土体会出现受拉趋势，当基坑开挖至高程388m以下时，在高程388～395m范围开挖边坡附近的土体中，出现最大-0.25MPa左右的拉应力。这些拉应力的出现，对于堰体和基础都是不利的。

基坑分级开挖对堰体和基础的应力水平有较大影响，但其等值线分布形状基本不变，随着基坑开挖深度的增加，堰基内部的应力水平有增大趋势。具体表现有两个方面，一是墙体中部上游侧高程387～407m范围内，随着开挖深度增加，该区域内的堰基应力水平逐渐增大，范围亦逐渐向上游侧扩展，直到基坑开挖至388m，新墙修建后，逐渐趋于稳定，最大应力水平达到1.0；二是对开挖边坡的影响，随着基坑开挖深度的增加，边坡附近土体的应力水平逐渐增大，当基坑开挖至392m以下时，在高程405m以下的开挖边坡内，应力水平已经大于0.85，随着开挖深度进一步加大，尤其挖至高程376m后，应力水平再进一步加大，当挖至高程368m时，应力水平最终达到1.0，故此可以认为开挖边坡存在失稳的危险。

堰体和基础的水平位移的等值线分布也较为规律，其值会随着基坑开挖深度的增加而增大。当基坑挖至高程388m以下，新墙修建后，堰基边坡附近的水平位移增大，且最大位移向上部移动，使边坡稳定性降低，最终在高程385～393m范围的开挖边坡附近，出现近40cm的最大水平位移。

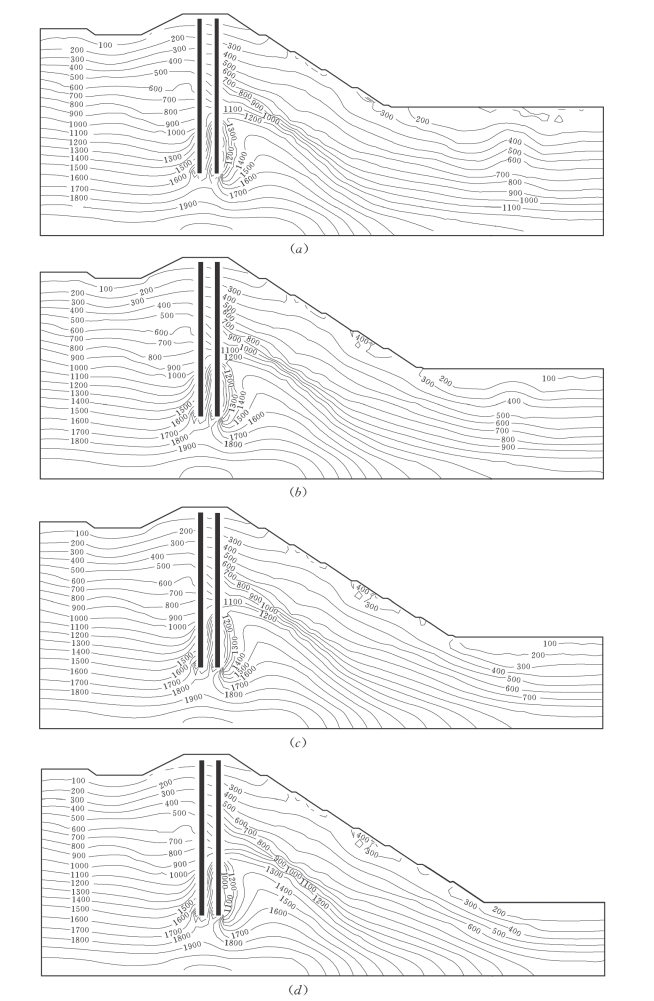
图7-66　不同开挖高程堰体第一主应力值线图（应力单位kPa）

（a）开挖高程384m；（b）开挖高程376m；（c）开挖高程368m；（d）开挖高程360m

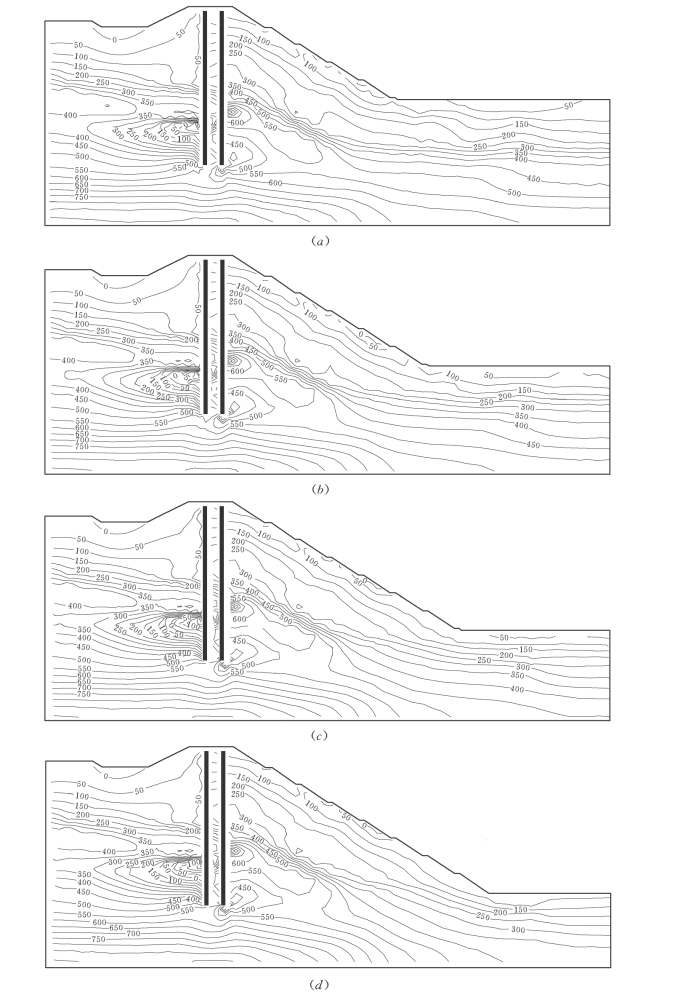
图7-67　不同开挖高程堰体第三主应力值线图（应力单位kPa）

（a）开挖高程384m；（b）开挖高程376m；（c）开挖高程368m；（d）开挖高程360m

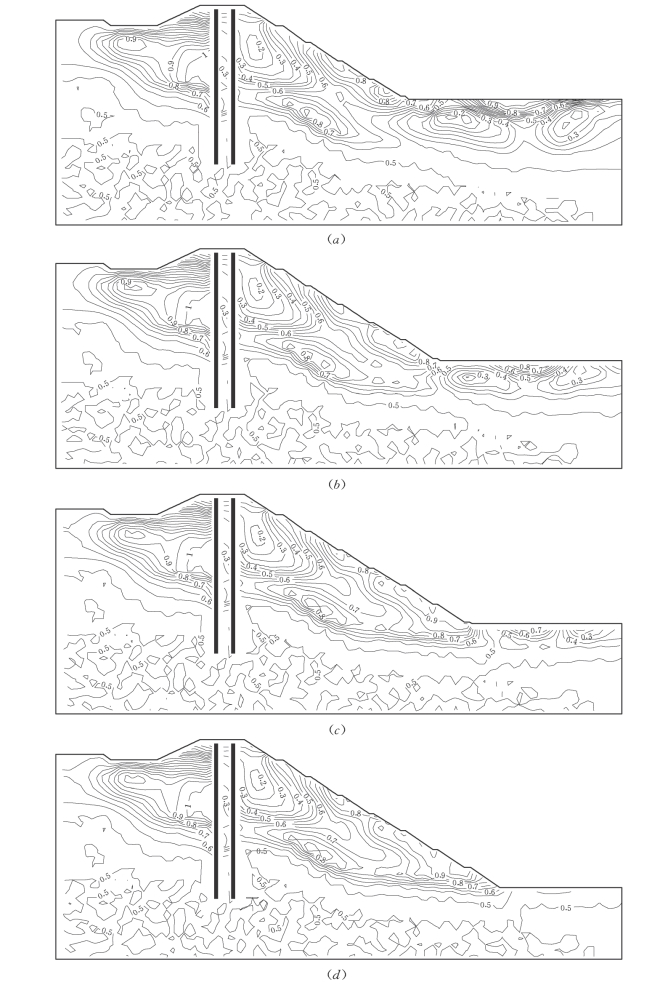
图7-68　不同开挖高程堰体应力水平等值线图（应力单位kPa）

（a）开挖高程384m；（b）开挖高程376m；（c）开挖高程368m；（d）开挖高程360m

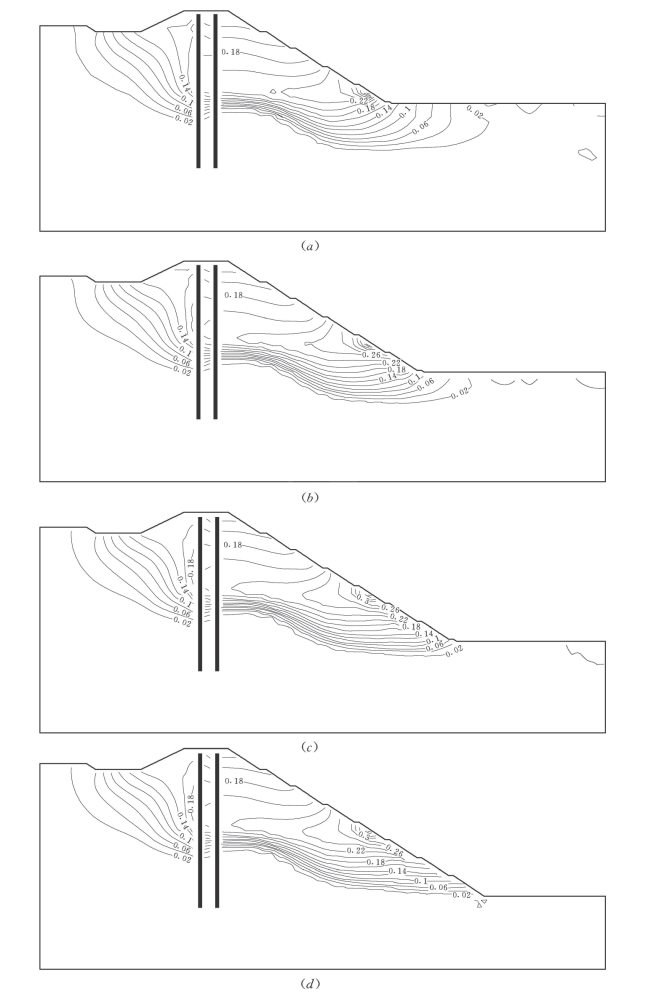
图7-69　不同开挖高程堰体水平位移值线图（单位m）

（a）开挖高程384m；（b）开挖高程376m；（c）开挖高程368m；（d）开挖高程360m

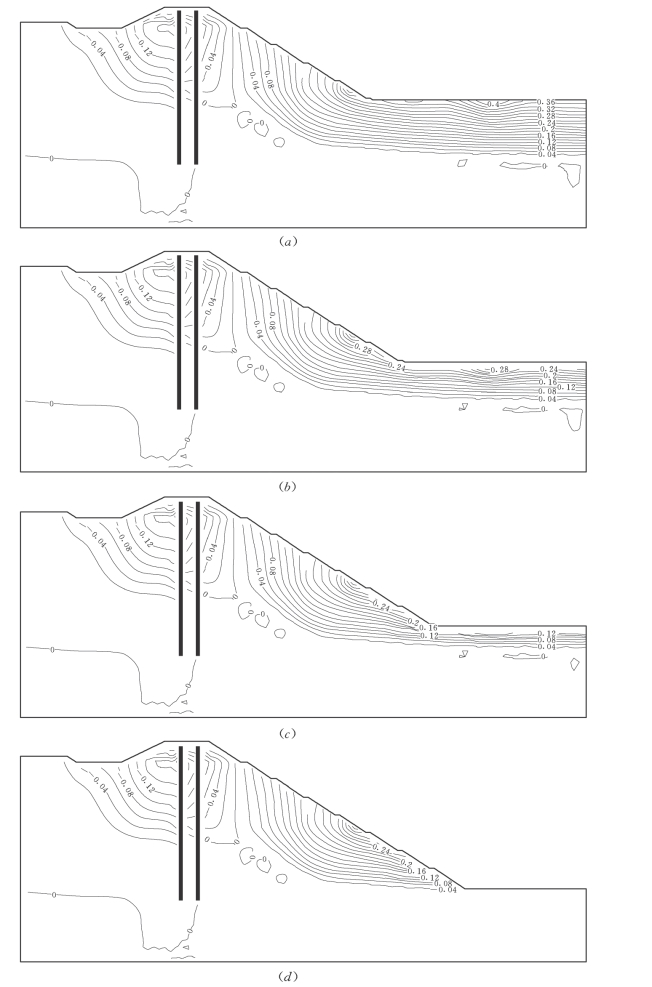
图7-70　不同开挖高程堰体垂直位移值线图（单位m）

（a）开挖高程384m；（b）开挖高程376m；（c）开挖高程368m；（d）开挖高程360m

堰体和堰基的垂直位移的等值线分布规律性亦很好，其值亦随着基坑开挖深度的增加而增大。当基坑挖至高程388m以下，新墙修建后，沉降量趋于稳定，在高程413～418m范围的新防渗墙上游侧土体内，出现最大近18cm的垂直沉降；当挖至高程392m以下时，在高程385～393m范围的开挖边坡附近，出现由于开挖所引起的最大35cm左右的抬升量。

（2）墙体应力变形分析。基坑的分级开挖对混凝土防渗墙的应力和变形均有影响，结果示于图7-71～图7-78和表7-47、表7-48中。可以看出，无论是应力、应力水平，还是变形，在各级开挖高程下，其随高程的分布曲线都是极为规律的。

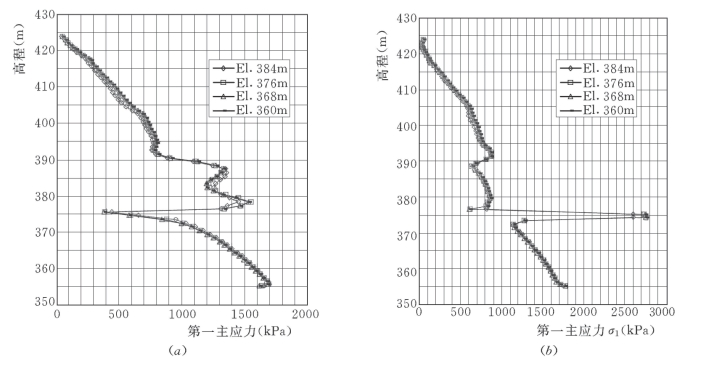
图7-71　新墙不同开挖高程第一主应力沿高程分布曲线图

（a）上游面；（b）下游面

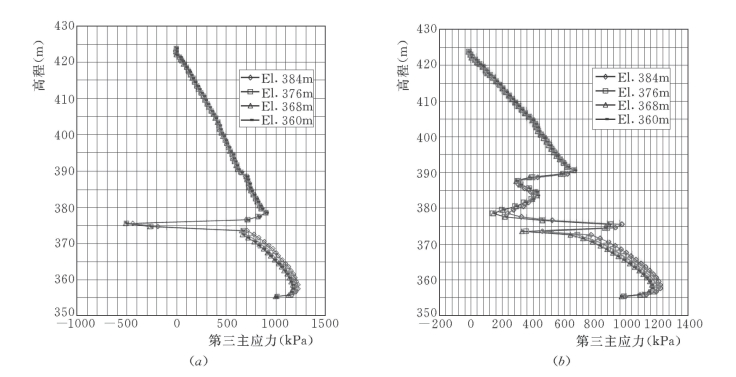
图7-72　新墙不同开挖高程第三主应力沿高程分布曲线图

（a）上游面；（b）下游面

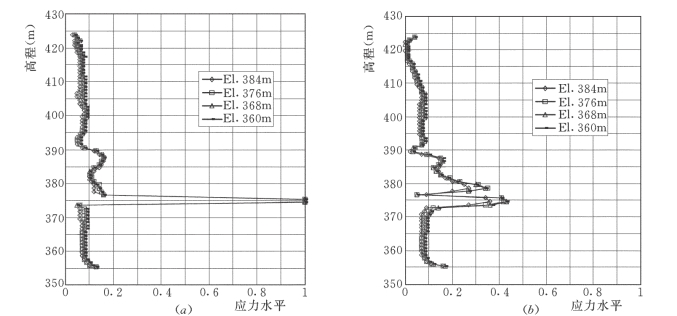
图7-73　新墙不同开挖高程应力水平沿高程分布曲线图

（a）上游面；（b）下游面

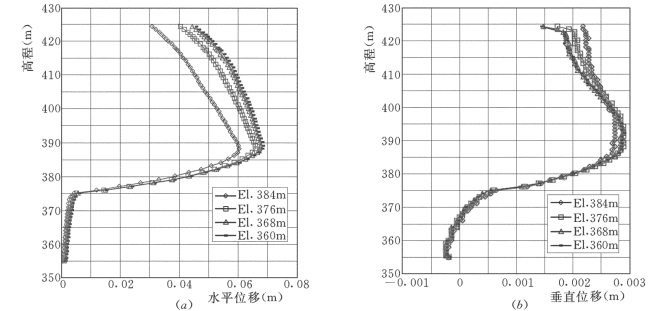
图7-74　新墙不同开挖高程位移沿高程分布曲线图

（a）上游面；（b）下游面

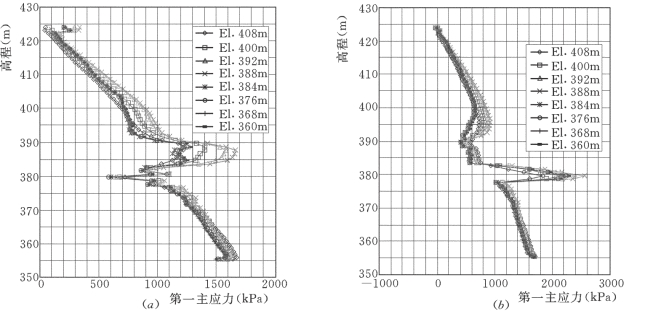
图7-75　老墙不同开挖高程第一主应力沿高程分布曲线图

（a）上游面；（b）下游面

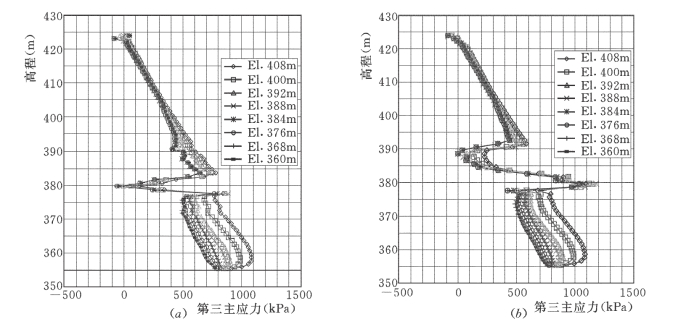
图7-76　老墙不同开挖高程第三主应力沿高程分布曲线图

（a）上游面；（b）下游面

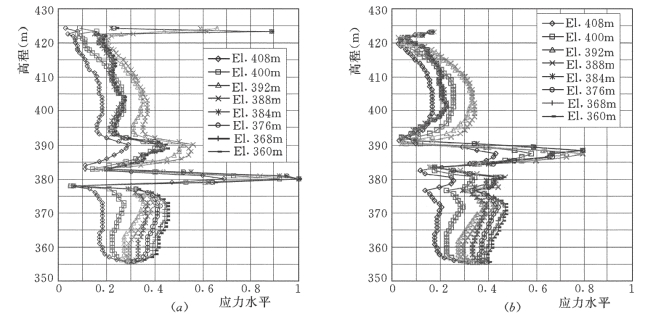
图7-77　老墙不同开挖高程应力水平沿高程分布曲线图

（a）上游面；（b）下游面

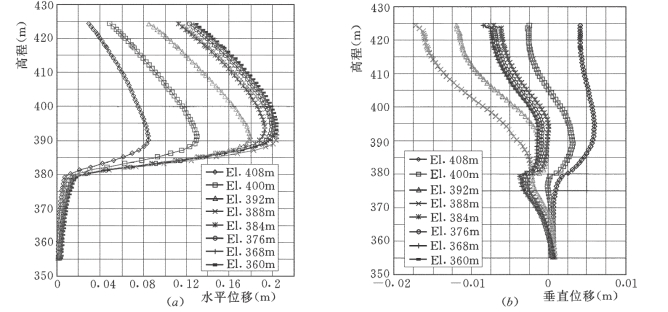
图7-78　老墙不同开挖高程位移沿高程分布曲线图

（a）上游面；（b）下游面

表7-47　方案No.13基坑分级开挖过程新墙应力分布特征值表

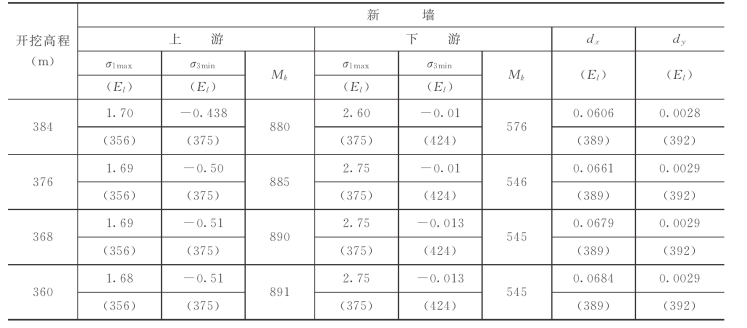
表7-48　方案No.13基坑分级开挖过程老墙应力分布特征值表

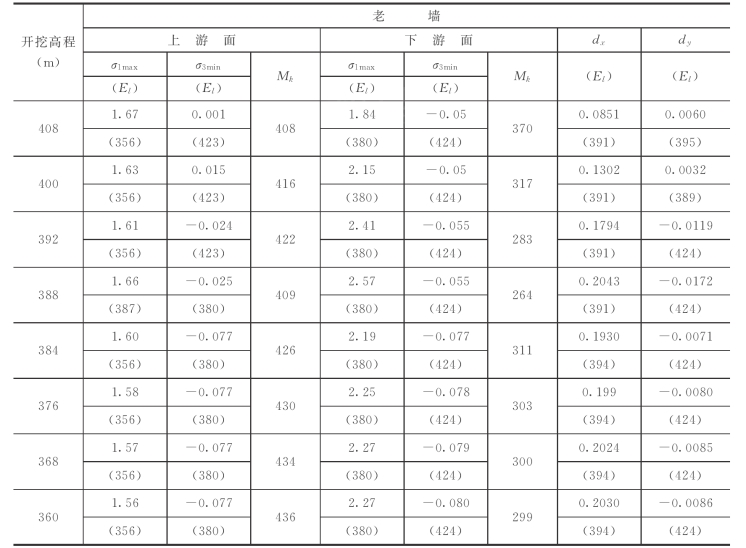
注　1.表中所列σ1max和σ3min分别表示大主应力与小主应力的最大值与最小值；dx表示墙体水平位移的最大值；dy表示墙体垂直位移最大值，其中正值表示抬升量，负值表示沉降量。
2.表中所列（El）表示对应特征值所发生的大致高程。
3.应力单位为MPa，位移单位为m，开挖高程单位为m，特征值发生的大致高程单位为m。
4.Mk=K/σ1max，称为模应比。

在基坑分级开挖过程中，各级开挖高程的墙体应力和变形的分布特征与基坑开挖至建基面360m时是一致的。由于新墙修建时基坑已开挖至高程388m，故此新墙的计算以高程384m为第一级。

新墙修建前，基坑的前期开挖对老墙的应力和变形影响较大。总体上讲，随着开挖深度的增加，老墙的应力、应力水平和变形都大幅度提高。其中，最大σ1由1.84MPa增加至2.57MPa，提高了40%；最小σ3由0.015MPa变为-0.025MPa，由受压变为受拉；最大应力水平由开挖至高程408m时的0.7增加到开挖至高程392m时的1.0，提高了43%，而且当开挖至384m时，老墙墙体顶部上游侧应力水平达到0.9，墙体中部389m高程处下游侧应力水平达0.8；最大水平位移由8.5cm增加至20.4cm，提高了140%；垂直位移也由0.6cm的抬升变为1.7cm的沉降。

新墙修建后，无论对老墙还是新墙，基坑的后期开挖对墙体的应力和变形影响都较小，对于新墙，最大σ1由2.60MPa增加至2.75MPa，仅提高了5.6%；最小σ3由-0.44MPa变为-0.51MPa，最大拉应力提高了16%；最大应力水平无变化，达到1.0；最大水平位移由6cm增加至6.8cm，仅提高了13%；最大垂直抬升量无变化。对于老墙，由于基坑中水位重新上升，致使老墙的应力和变形先有小幅度的降低，由2.57MPa降至2.19MPa；最大σ1由2.19MPa增加至2.27MPa，仅提高了3.8%；最小σ3由-0.077MPa变为-0.08MPa，表示最大拉应力提高了4%；最大应力水平无变化，始终为1.0；最大水平位移由19.3cm增加至20.3cm，仅提高了5.2%；最大垂直沉降量由0.71cm增加至0.86cm，仅提高21%。