1.计算断面
根据山西横泉水库拦河大坝的特点,对大坝的三个断面进行了非线性有限元计算,这三个断面的桩号分别是0+112.5,0+412.5,0+562.5,其横断面分别见图7-8~图7-10。
由于各个断面的地质条件存在差异,地质情况比较复杂,故为了计算方便,有必要对各个断面进行一些简化,具体如下:

(2)由于防渗墙顶端的高塑性土,防渗墙底部的灌浆帷幕与坝趾处的排水棱体的面积相对较小,且缺乏相对可靠的土工参数,故计算中忽略其影响。
2.计算方案
为了研究混凝土防渗墙墙体材料的弹性模量K对防渗墙应力和变形的影响,对每一个计算断面,分别拟定了蓄水后防渗墙的几种不同计算方案,进行敏感性分析。
由于0+412.5与0+562.5两个断面的防渗墙在设计上布置于坝轴线的上游侧,使得在坝体填筑的过程中,墙体的上下游面所受到的土压力不均衡,下游面的土体作用大于其上游面,这就造成了防渗墙在蓄水前主要向上游侧发生水平变形,墙体受到较大的剪应力,其应力水平较蓄水后偏高。如果不能很好地控制墙体混凝土的模量,当其模量过高时,势必造成墙体出现大量的、连续的剪切破坏面,影响防渗墙的安全性。因此对这两个断面进行了蓄水前防渗墙的应力应变计算。这两个断面计算结果接近,为简化起见,文中仅列出0+562.5断面的计算情况。
各计算方案及K值拟定如表7-14所示。
3.网格划分
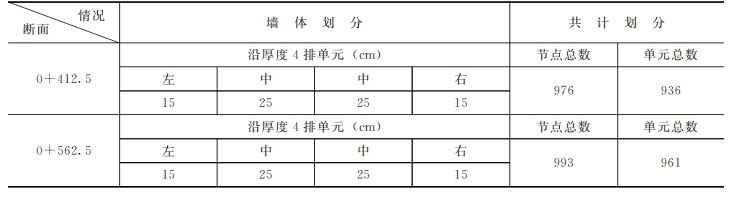
各个断面的网格划分如图7-11~图7-13所示。为了反映边界对计算结果的影响,将计算范围在水平和垂直方向进行了延伸,其中水平方向向上下游方向各延伸一半坝底宽度,垂直方向向下延伸一倍坝高,且延伸至防渗墙底2~3排单元。划分网格时,除了边角与不同材料的交界面上采用了少数的三角形单元外,其余大部分都采用四边形单元。由于本研究的主要对象是防渗墙,所以对防渗墙部位的网格进行了细化。各个断面的具体网格划分情况见表7-15。
4.材料参数

图7-8 0+112.5断面大坝剖面图(高程:m;尺寸:mm)
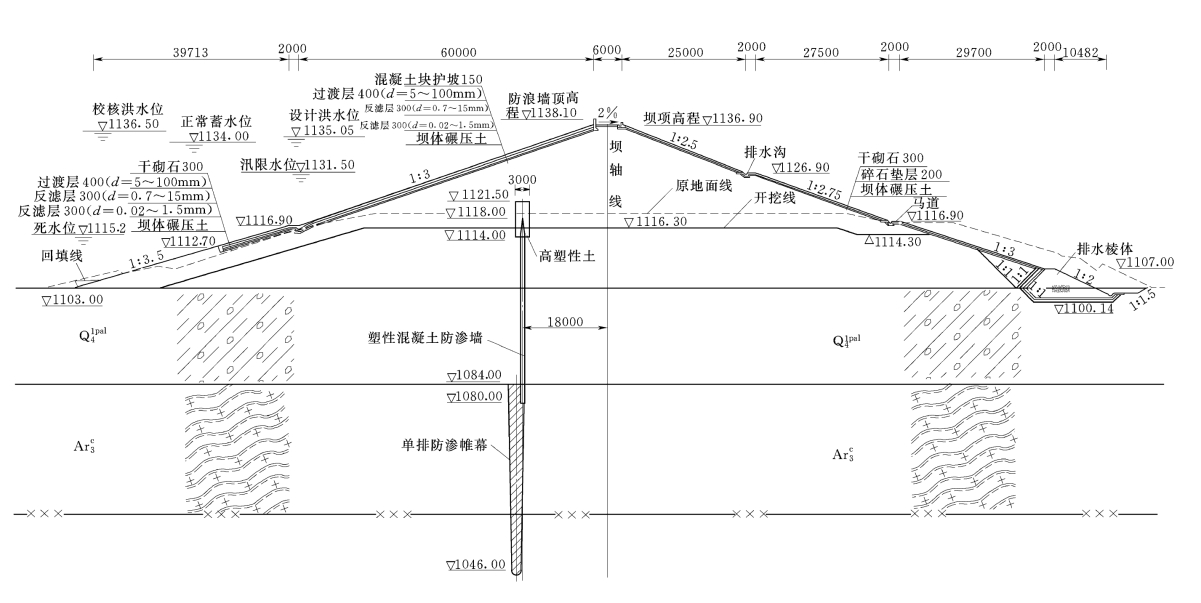
图7-9 0+412.5断面大坝剖面图(高程:m;尺寸:mm)

图7-10 0+562.5断面大坝剖面图(高程:m;尺寸:mm)
表7-14 各断面计算方案K值拟定表
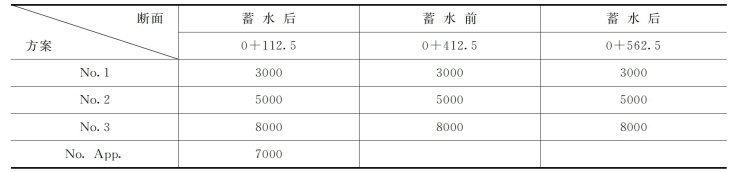
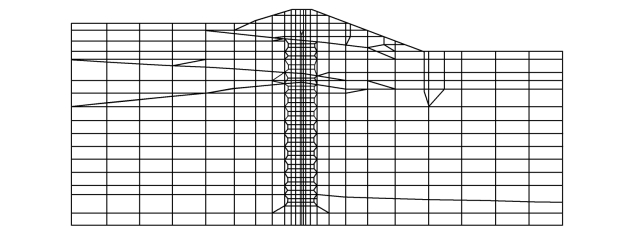
图7-11 0+112.5断面有限元计算网格图

图7-12 0+412.5断面有限元计算网格图
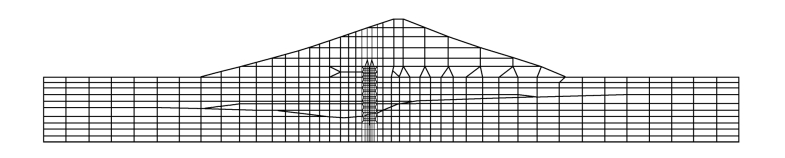
图7-13 0+562.5断面有限元计算网格图
表7-15 各断面网格划分情况表

续表
横泉水库工程三个断面的防渗墙分析中,共涉及到11种材料,包括坝基强风化岩、坝基覆盖土、 原状土、
原状土、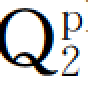 强夯土、
强夯土、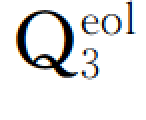 原状土、
原状土、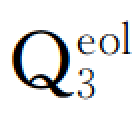 强夯土、旧坝体填土、旧坝体强夯土、坝体新填土、塑性混凝土和泥皮接触面。其中,除塑性混凝土和接触面外,其他所有材料试验均由水利部山西省水利水电勘测设计研究院完成,清华大学水利水电工程系根据试验参数,通过计算和工程类比确定材料的邓肯·张参数;塑性混凝土和接触面的参数由清华大学水利水电工程系根据工程类比拟定;山西省院后期还补充提供了左岸黄土台地经过强夯后的土工数据。
强夯土、旧坝体填土、旧坝体强夯土、坝体新填土、塑性混凝土和泥皮接触面。其中,除塑性混凝土和接触面外,其他所有材料试验均由水利部山西省水利水电勘测设计研究院完成,清华大学水利水电工程系根据试验参数,通过计算和工程类比确定材料的邓肯·张参数;塑性混凝土和接触面的参数由清华大学水利水电工程系根据工程类比拟定;山西省院后期还补充提供了左岸黄土台地经过强夯后的土工数据。
最终所选的计算材料参数见表7-16。
表7-16 横泉水库塑性防渗墙有限元计算材料参数总表

5.计算模型
(1)Goodman一维滑动模型。防渗墙体与两侧土体的接触面采用Goodman一维滑动模型,其接触面切向刚度系数为

式中kst——接触面切向刚度系数;
γw——水的容重;
Pa——大气压强;
σn——法向正应力;
τs——切向剪应力;
K1,n1,Rf1,c1,δ——由剪切试验确定的参数。
此外,作如下规定:
当接触面受压,σn>0时,令kn=9.8×108kN/m3;(https://www.daowen.com)
当接触面受拉,σn<0时,令kn=9.8kN/m3,kst=9.8kN/m3。
(2)Duncan and Chang E—B模型。除上述接触面外,其他材料均采用Duncan and Chang E—B非线性模型,其弹性模量、体积模量和卸载模量分别为

式中 K——弹性模量数;
Kb——体积模量数;
Kur——卸载弹性模量数;
n——弹性模量指数;
m——体积模量指数;
c——黏聚力;
φ——内摩擦角;
Pa——大气压强。
此外,作如下规定:
1)Kur=1.2K。
2)加载时,限制μ=0时,B=E/3。
卸载时,限制μ=1/3时,B=E。

然后,将SLc与土体当前的应力水平SL进行比较,并据此进行判断如下:
当SL≥SLc时,为加载,取Et。
当SL≤0.75SLc时,为卸载,取Eur。
当0.75SLc<SL<SLc时,可按式(7-11)进行线性插值计算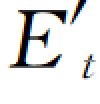
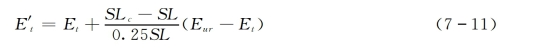
6.计算程序
本实例主要采用大坝及基础工程结构分析通用程序软件包GPDFA2005进行计算,该程序曾对三峡二期双低塑性混凝土防渗墙、黄壁庄水库副坝防渗墙等工程进行过非线性计算分析,取得了很好的结果。
7.分期加载
为了能模拟施工和蓄水过程,针对各个断面采用不同的加载过程,具体如下:
(1)0+112.5断面。
1)计算基础先期应力,同时模拟基础的现状,考虑基础已经沉降完成,将此步计算得到的应变与变形置为0。
2)填筑坝体至高程1128.5m。
3)修建塑性混凝土防渗墙。
4)填筑坝体至坝顶高程1136.9m。
5)蓄水至正常蓄水位高程1134.0m,形成稳定渗流场。
(2)0+412.5断面。
1)计算基础与旧坝体先期应力,并考虑基础与旧坝体已经沉降完成,将计算得到的应变与变形置为0。
2)填筑坝体至高程1119.5m。
3)修建塑性混凝土防渗墙。
4)填筑坝体至坝顶高程1136.9m。
5)蓄水至正常蓄水位高程1134.0m,形成稳定渗流场。
(3)0+562.5断面。
1)计算基础先期应力,同时模拟基础的现状,考虑基础已经沉降完成,将此步计算得到的应变与变形置为0。
2)填筑坝体至高程1107.0m。
3)修建塑性混凝土防渗墙。
4)填筑坝体至坝顶高程1136.9m。
5)蓄水至正常蓄水位高程1134.0m,形成稳定渗流场。
需要说明的是,我们选取的计算条件,各个断面均为正常蓄水位1134.0m。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





