工程中常常遇到土与其他材料的结构物的相互接触的问题。要了解土体与（水工）建筑物的相互作用，首先要了解两者接触面的力学性能。由于两种材料变形不一致，会在接触面上产生较大的剪应变，并有可能出现滑移破坏。接触面上的受力变形又影响到土与建筑物中的应力状态。有些结构对此又相当敏感（譬如混凝土防渗墙）。因此把握好接触面上的应力、应变规律是十分重要的。

（一）单元模型

早在1968年，Goodman等人［3］就提出采用无厚度接触面单元模拟接触面；1970年，Zienkiewicz等人又提出了有限厚度接触面单元。在他们的工作之后，Ghaboussi［29］提出了以接触面相对位移为自由度的接触面单元，克服了有些接触面单元由于长宽比过大产生的数值计算上的困难；Desai［30～32］通过试验发现，接触面的力学特性和接触面附近土体的力学特性有关，认为用薄层单元模拟接触面比较合理，但是，对Desai的薄层单元也持有否定态度的，他们认为土与混凝土接触面处设置薄层单元是虚构的，是一个错误的物理概念。文献［33］认为，Desai等人提出的薄层单元及相应的力学模型应该用于描述一些夹层材料的性质，而土与混凝土的接触面应该以无厚度接触面单元模拟。

中国水利水电科学研究院在1990年的试验研究成果［34］为我们选定接触面单元型态提供了依据。文献［33］通过双层土试样共振柱试验，研究了粗糙接触面对一种细砾动剪模量的影响，发现并证实在紧贴接触面的土体中存在着一层边界层，它的动剪模量远远大于土本身的值。边界层内土体的剪应变实际上可取为零，也就是说，边界层与混凝土建筑物一起运动。而且，边界层的厚度较小，最大只有0.01m。试验指出，在剪应变幅度为10-6～10-3的范围内，边界层现象都存在着。

对于土工建筑物和周围土体的接触面而言，在混凝土与土体之间也存在着上述边界层。对于实际工程，不论是相对于混凝土的厚度还是相对于土体的厚度（无限大），边界层的厚度都是一个微量，它对土体的动剪模量的影响完全可以忽略［34］。而且，由于边界层模量远远高于附近的土体的相应值，因此我们可以把边界层看成混凝土的一部分，由于边界层的厚度很小，这样做并不会影响混凝土结构的力学特性。经过上述处理之后，我们就可以采用Goodman提出的无厚度的接触面单元来模拟混凝土与土体的接触面。Goodman单元模型参见本章第一节。

（二）接触面力学模型

早期，对于土与混凝土或其他结构的接触面多用刚塑性模型，试验研究多集中于确定接触面的摩擦系数。随着有限元计算方法在土与建筑物相互作用问题研究中的应用和发展，人们开始对接触面的应力应变关系进行研究［35］。

由于接触面上的土体不能嵌入混凝土之内，所以接触面的法向应力与法向相对位移的关系比较简单。通常，根据数值计算中不引起方程病态的原则而假定接触面法向刚度很大，一般采用法向刚度系数kn=1010～1012N/m3内的数值，我们在计算中选取kn=1011N/m3。而土与混凝土接触面的剪应力与相对位移（剪应变）的关系很复杂，不同的学者得到了不同的表达式。有关的试验研究结果通常归纳为某种剪应力与相对位移关系模型，以便在计算中应用，常用的有以下三种：

（1）双曲线模型。Clough和邓肯［4］在盒式直剪仪进行了砂与光滑混凝土接触面的剪应力与位移关系研究。在试验的基础上提出双曲线模型，如图5-31所示，这也是目前应用最为广泛的模型之一，具体内容可参见本章第一节。

（2）弹塑性模型。Brandt［36］进行的室内接触面盒式直剪仪试验以及对一座试验挡土墙的现场观测结果表明，土与混凝土接触面的剪应力与位移关系可近似用两条进直线表示，如图5-32所示。

当φf值很小时，这就是弹塑性模式。

图5-31　双曲线模型

图5-32　弹塑性模型(www.daowen.com)

图5-33　刚塑性模型

（3）刚塑性模型。刚塑性模型是经典土力学中计算挡土压力时所采用的接触面剪应力与位移关系模型。如图5-33所示。

该模型认为在剪应力τ达到抗剪强度τf之前，接触面上不发生任何相对位移，即u=0；而达到抗剪强度以后，位移的发展与剪应力无关。

关于接触面的试验大多是在直剪仪上做的。这就隐含了这样一个前提：即认为接触面就是与土相接触的混凝土材料表面。这仅在材料表面十分光滑平整时才是正确的，因为只有在这种条件下，才会沿材料表面发生剪切破坏。而水利或土木工程中与土体相接触的混凝土（特别是防渗墙的）表面大多是粗糙的，除法向应力较低的情况外，沿接触面的剪切破坏往往发生在邻近接触面的土体中，破坏面不是某一个预先可知的确定的面［35］。直剪试验不能反映真实粗糙接触面的力学性能。其次，这些试验量测的切向位移实际上包括了土体沿切向的压缩变形，并不只是接触面的相对位移。另外，接触面的破坏实际上是从一点的破坏开始的，直剪试验中试样接触面上的相对位移，实际上是接触面剪切破坏区逐步发展的结果，而且，相对位移与破坏区域发展的长度有关。文献［37］给出的研究表面，在法向应力相同的情况下，改变试样的尺寸，得到的剪应力与相对位移曲线是有很大不同的，见图5-34。

所以，直剪仪上测定的接触面上的强度及应力与位移关系均不易真实地反映接触面的特性，因而也不能用于有限元计算。

我们知道，对于接触面上的某一点的剪应力来讲，剪应力与相对位移的关系，实际上就是如图5-33那样，当τ＜τf时，u=0；当τ=τf时，出现错动，u＞0且不断发展。也就是说，接触面上每一点只可能存在两种状态：未滑动，已滑动。因此，对于接触面上每一点来讲，刚塑性的力学模型是唯一能正确反映其真实特性的应力与位移模型。

当然，用适用于接触面上一点的刚塑性模型描述整个接触面是不准确的。然而有限元的方法为我们应用刚塑性模型描述接触面的力学特性提供了手段。将整个接触面离散成为许多长度很小的单元，那么，每一个单元只可能出现三种情况：

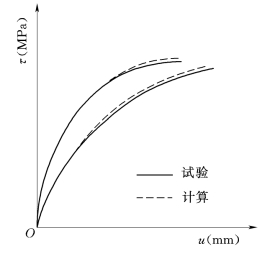
图5-34　不同试验尺寸时的τ—u关系

（1）剪应力较小，沿单元长度上无一处达到τf，故无任何相对错动，此时单元的切向刚度系数ks（ks=τ/u）可以取很大的值，如1010N/m3，在数值上实现刚性。

（2）剪应力相当大，沿单元长度方向处处达到τf，因而处处存在错动，其相对位移的大小与剪应力无关，而由周围的约束条件决定。理论上讲，此时ks=0，而在计算中取一个很小的值以防方程组出现病态。

（3）介于两者之间，单元在局部范围内τ达到τf，存在相对位移，而另一部分τ＜τf，没有相对位移。显然，与直剪试验中的试样相似，单元相对位移的大小与剪破区的长度有关。

实际上，当单元划分足够细密时，我们可以认为单元只存在前两种情况，也就是说，我们可以近似地把每一个接触面单元概化为一个点，这样应用刚塑性模型描述单元的性能虽然不能做到完全准确，但也可以做到足够准确。

本节在进行防渗墙的计算研究时，就是采用了应力与位移关系的刚塑性接触面模型。如前所述，土与混凝土接触面剪切破坏发生在邻近的土体中［33，36］，因此，我们选取接触面的抗剪强度与附近土体的抗剪强度相等。应该明确，我们在有限元计算时将整个接触面离散为若干单元而采用刚塑性模型，与早期的对整个接触面采用刚塑性模型是有本质区别的。