（一）动力平衡方程

当结构的基础受有加速度为üg（t）的地震运动时，其动力平衡方程为

求解土与混凝土结构的动应力、动变形问题，关键就是求解动力平衡方程式（5-55）的问题。本节采用集中质量矩阵。将系统的质量分别集中到各个节点上，而且不考虑节点的转动。因此，每个自由节点只有两个平动自由度，而系统的整体集中质量矩阵［M］则为对角矩阵。

对于阻尼随单元应变而变化的情况，整体阻尼矩阵［C］由单元阻尼矩阵［c］集成得到。对于某单元e，其单元阻尼矩阵［c］可以采用Rayleigh阻尼的表达形式写成

式中［m］、［k］——该单元的质量阵和刚度阵；

a、b——参数，阻尼值和单元刚度特性的函数，可以用式（5-57）求得

式中　D——单元e的阻尼比，对于土及塑性混凝土，D随该单元动应变的发展而变化；

ω1——系统的基本频率，可通过逆迭代法求解特征方程［K］｛φ｝n=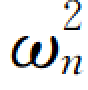［M］｛φ｝n得到的（n=1）。

将各单元的阻尼矩阵集成就可以得到整体阻尼矩阵［C］，显然，［C］是对称的稀疏阵。而且，［C］是随各单元的动应变的发展而不断变化的。

总体刚度矩阵［K］也是由单元刚度矩阵［k］集成而得到。对于单元e，其单元刚度矩阵为

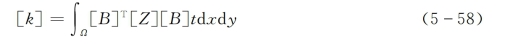
式中　Ω——单元面积；

B——几何矩阵；

t——单元厚度，通常取t=1m；

［Z］——弹性矩阵，在平面应变问题下，为

式中　G——动剪模量；Z1=2（1-μ）/（1-2μ），Z2=2μ/（1-2μ），μ为泊松比。

对于土与塑性混凝土，随单元应变的发展，其动模量G不断变化，因而其单元刚度矩阵也随着改变。所以，整体刚度矩阵在地震过程中也是时刻在变化的。

以上的分析表明，由于土及塑性混凝土等材料具有动模量及阻尼比随动应变而变化的动力非线性性质，使得混凝土防渗墙与围土系统也存在着动力非线性的性质，表现为系统的刚度矩阵和阻尼矩阵在地震过程中是不断变化的。这是非线性系统与线性系统的根本区别，也正是土与防渗墙动力相互作用研究的主要特点。

（二）动力平衡方程的数值解法

通常，在线性体系的框架下，人们常按照叠加原理来分析结构的动力反应，利用振型的正交特性，将多自由度体系耦联的动力方程组分解为一系列解耦的单自由度问题，然后采用基于时域的Duhamel积分法或者基于频域的Fourier变换法来求解动力平衡方程。

这里，由于地震荷载的复杂性和结构体系的动力非线性，使得叠加原理不再适用，故此考虑采用时域直接逐步积分法来求解动力平衡方程，即将输入的地震加速度时间过程离散化，用逐步积分的方法直接从方程式（5-55）求出位移和应力的历程响应。目前已经发展了一系列的求解结构动力平衡方程的时域直接逐步积分法，常用的包括中心差分法、Newmark-β法和Wilson-θ法等，下面作一简要介绍。

1.中心差分法［25］

中心差分法基于有限差分来代替位移对时间的微分，当采用等时间步长时，Δti=dt时，则可以得到速度和加速度的中心差分为

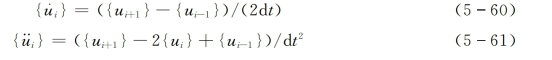
而离散时间点的运动为

将式（5-60）和式（5-61）代入动力平衡方程式（5-55），再进行展开，整理得到ti+1时刻的位移为求得ti+1时刻的位移后，再利用式（5-60）和（5-61）就可以求得ti+1时刻的速度和加速度。

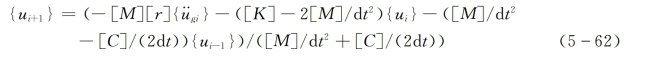
显然，中心差分法在计算ti+1时刻的响应时，需要知道前面两个时刻，即ti和ti-1时刻的响应，属于两步法，存在起步问题。这里我们主要研究结构系统在地震作用下的响应问题，一般可假设初始两个时刻（i=-1和i=0）的位移都为0（u-1=0和u0=0），即可进行计算。中心差分法给出的稳定性条件为dt≤Tn/π，Tn为结构系统的最小自振周期。

可以发现，由于我们在这里采用的是Rayleigh阻尼，所得到的整体的阻尼矩阵为稀疏对称的非对角阵，采用中心差分法计算时，方程组并不解耦，使其成为隐式方法，将失去显式中心差分法计算效率高的优点，不建议采用。(www.daowen.com)

2.Newmark-β法［25］

Newmark-β法同样将时间离散化，给出ti～ti+1时段内加速度的变化规律假设，以ti时刻的动力响应为初值，通过积分推求ti+1时刻的动力响应。

已知离散时间点ti和ti+1时刻的加速度为｛üi｝和｛üi+1｝，Newmark-β法假设在ti～ti+1时段内的加速度值为介于二者之间的常量｛a｝，可由式（5-63）给出

为了得到稳定和高精度的算法，｛a｝用另一控制参数β表示为

在ti～ti+1时段上对加速度｛a｝进行积分，可以得到ti+1时刻的速度和位移为

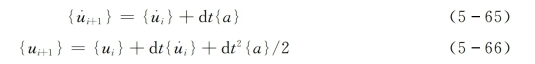
将式（5-63）代入式（5-65），式（5-64）代入式（5-66），并整理得到ti+1时刻的加速度和速度为

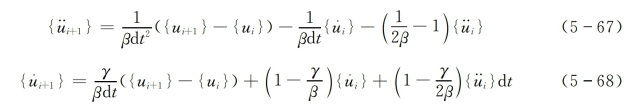
将式（5-67）和式（5-68）代入动力平衡方程，即

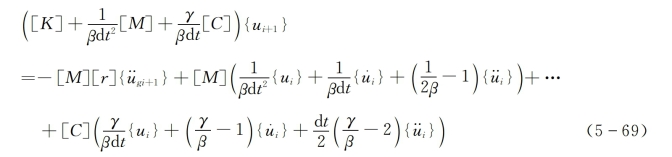
由式（5-69）即可求得ti+1时刻的位移｛ui+1｝，然后再利用式（5-67）和式（5-68）就可求得ti+1时刻的加速度和速度。

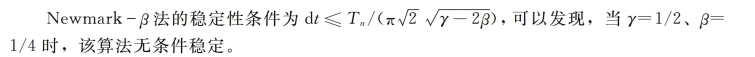
3.Wilson-θ法［25，26］

Wilson-θ法是在线性加速度法的基础上发展起来的一种数值积分方法，其假定加速度响应从时刻t～t+θdt内为线性变化（如图5-29所示），其中，θ≥1.0。

令τ为由时刻ti算起的局部时间坐标，即是0≤τ≤θdt，则t～t+θdt时段内的线性加速度可以表示为

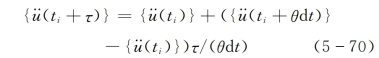
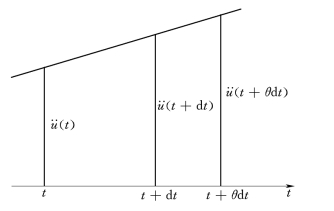
图5-29　Wilson-θ法线性加速度假定

对上式积分，得

将式（5-74）至式（5-76）代入式（5-73），得到

FEASSI程序即是采用上述的Wilson-θ法，为了达到无条件稳定，必须使θ＞1.37，通常取为1.40。

（三）动力非线性计算

如何处理动力非线性问题，是求解土与结构动力相互作用问题的一个关键技术，它直接关系到计算工作量、解答的精度和正确性等许多方面。

在上述的求解过程中，对于土及塑性混凝土的非线性的处理，一般可采用两种方法：真非线性方法和等效线性方法。

真非线性方法是以试验或假定的骨干曲线、卸荷和重加荷曲线来表示材料的动力应力应变关系，在计算时，对每一个dt，假定其G、D不变，从而根据该时间步初加荷、卸荷或重加荷时的应变值确定每个单元的动模量G和阻尼比D，形成该dt内系统的整体刚度和阻尼矩阵，然后用逐步积分方法求解各节点的运动状态，进而得到各单元的应力应变状态。显然，这种方法的计算精度取决于dt的大小，dt越小，精度越高，为了达到较高的精度，计算工作量是巨大，用它来求解规模较大或较复杂的水利工程问题要花费相当可观的计算机时和资金，所以一般都不轻易采用。

等效线性方法，就是以骨干曲线表示材料的非线性动应力应变关系，将响应过程划分为若干个修改模量时段Δt（包括许多时步dt），在Δt内，认为材料的G、D均为常量且人为给定一初始值，对每一个dt进行动力分析直至Δt结束，求出每个单元的最大应变γ以及与之相应的动模量G'和阻尼比D'的值，通过不断迭代使各单元在计算中所设用的G、D与根据γ从骨干曲线上确定的G'和D'相一致。具体的做法如图5-30所示。

不难看出，等效线性方法使我们在计算非线性系统时，可以节省大量的机时和资金，而且，这种方法求得的动力响应的最大值是可信的，在程序FEASSI中我们即采用了这种方法。

在程序FEASSI中，将非线性动应力应变关系、阻尼特性分别表示G/G0—γ、D—γ的关系曲线（试验曲线或假定曲线），通过数值方法离散而读入计算机。因此，动力计算的初始数据主要是如何确定各单元的起始动剪模量G0的问题。对于黏性土，G0=SuK1，其中Su为不排水剪切强度，系数K1在1000～5000的范围内变化［27］。Su、K1可以由试验确定。对于砂性土，G0=22K2（σ'）1/2（×0.1MPa），其中，σ'为单元的平均有效主应力（×0.1MPa），由静力计算求得；K2则是动力性质常数（砂土的K2=35～70，砂卵石的K2=70～190）可以由试验得到或根据材料的相对密度选取［28］。塑性混凝土的G0的确定参见第三章。

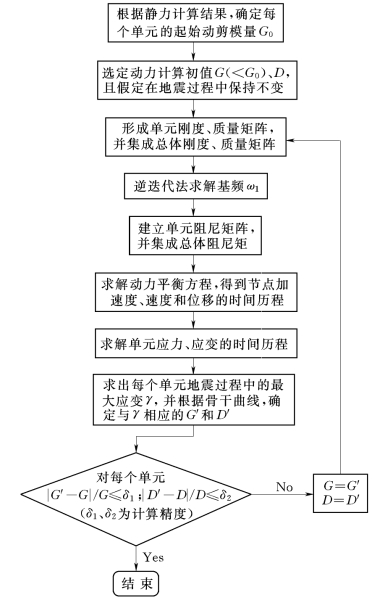
图5-30　等效线性方法