数值仿真计算的精度，不仅与计算模型和计算程序有关，而且在很大的程度上与计算参数的选取有关。邓肯·张E—B模型涉及到8个计算参数，邓肯·张E—μ模型涉及到9个计算参数，Goodman模型涉及到5个计算参数，所有这些参数都需要通过试验加以标定，但由于试验取样、试验设备、试验方法、试验人员的水平等诸多随机因素的影响，使得这些参数的取值范围变化较大，从而影响到计算结果的精度，即存在参数敏感性问题。

进行参数敏感性分析，一般都是通过逐一或者同时变换单个或者多个计算参数，形成多种组合计算方案，再对各方案的计算结果进行综合分析比较，找出规律性的结论，从而确定各个参数的变化对计算结果的影响，比较各个参数敏感性水平的高低。

三峡开发总公司和长江水利委员会长江科学院曾对三峡二期围堰进行过参数敏感性分析［11］，为参数的优化反演分析和围堰的反馈分析提供依据。三峡二期围堰填料中的风化砂、石渣堆石和反滤层材料采用邓肯·张E—μ模型，共有3×8=24个计算参数，再加上各自的密度ρd，共27个计算参数，其中c、φ和ρd在试验室确定，反馈分析中不予考虑，其他共有18个参数，这些参数中必有一些对应力变形比较敏感，有些则相对不敏感。

设给定参数X=｛Rf.K.n.G.F.D｝，计算可变参数对防渗墙最大位移Dmax的影响，记为F=｛Dmax｝。定义敏感度因子αi=|ΔF/F*|/|Δxi/xi|，其中，xi为某一系统特性参数，F为系统特性，“*”表示实测值。

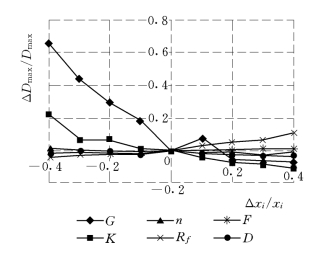
图5-18　风化砂各参数∆Dmax/Dmax—Δxi/xi关系曲线

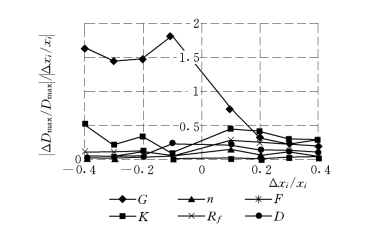
图5-19　风化砂|ΔDmax/Dmax|/|Δxi/xi|—Δx/xi关系曲线

图5-18、图5-19和图5-20分别为风化砂和石渣的各个参数的ΔD/D—Δxi/xi的关系曲线。从中可以看出，对于风化砂材料，以参数G的曲线斜率最陡，其次为K和Rf；对于石渣，以K的影响程度最大，其次为G。另外，对于反滤层，以参数G的影响程度最大，其次为Rf。这种影响程度，除与材料特性有关外，还与材料在围堰中所处的位置有关。

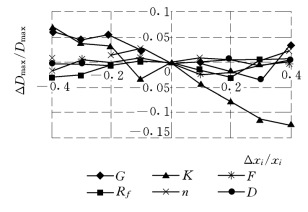
图5-20　石渣堆石各参数ΔDmax/Dmax—Δxi/xi关系曲线

上述三种材料的敏感度因子列于表5-3中。从中可以看出，对于风化砂，G、K、Rf的敏感度较高；对于石渣，G、K的敏感度较高；对于反滤层，G的敏感度较高。

表5-3　邓肯·张模型系数的敏感度因子

四川大学的何昌荣教授［12］依据试验数据，分别变化邓肯·张E—μ模型中的各个参数，对某一土坝的应力应变进行计算，较为系统的对E—μ模型进行了参数敏感性研究。

图5-21和图5-22中，给出了各参数的变化与位移变化的关系曲线，从中可以看出，G、φ的敏感度较高，特别是G、φ减小时，位移增减曲线的斜率较陡，说明G、φ的微小变化可能会引起位移的较大变化；其余参数的敏感度相对较低。何教授提到，φ在试验和整理分析时，已经包含有一定的误差，试验人员依据各种情况提出建议，进行一定折减，设计计算人员使用时，还要进行折减，这使得φ的变化幅度可达10%～40%；同时，对于大多数土体，G的变化范围常在0.25～0.50之间，计算使用值与实际值相差10%～30%常见；故此，对这两个参数应予以足够的重视。

何教授还认为，K的敏感度虽然不及G、φ高，但由于实际计算中K的变化幅度通常可达数倍甚至几十倍，也能引起计算结果的成倍偏差，因此也应予以充分重视。造成这一现象的主要原因是K的试验取值和原本的物理意义不符。邓肯·张模型中所定义的K的物理意义是围压σ3=Pa的情况下的初始模量Ei，即轴向应变εa趋于零时的模量，这就要求在试验过程中尽可能的量测到微小的轴向应变，但由于试验设备精度和数据整理分析方面的原因，通常只能量测到εa=10-3量级的轴向应变，于是造成了K的取值的成倍差异。

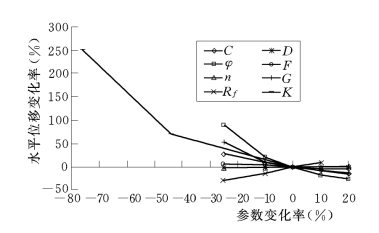
图5-21　各参数与水平位移的关系曲线

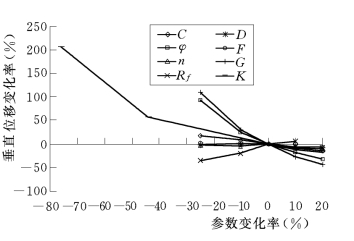
图5-22　各参数与竖向位移的关系曲线

以上给出的均是邓肯·张模型中各参数的变化对土体变形和应力的影响，除此以外，各参数的变化对墙体的应力也会造成影响，下面结合我们的研究工作加以说明。

通过对山西横泉水库大坝塑性混凝土防渗墙的应力变形分析［13］，发现防渗墙的K的取值变化对各计算断面墙体最大压应力（σ1max）有较大影响，如图5-23所示。从中可以看出，各计算断面防渗墙上下游面的最大压应力均随着K的增加而增大，当K的增加范围在2倍以内时，最大压应力的增大的变化范围为0～40%。(www.daowen.com)

研究同时发现，随着K的增大，防渗墙的上游侧的应力状态由受压转为受拉，表明受拉程度明显增加。这些都说明横泉水库大坝塑性混凝土防渗墙的K值具有较高的敏感性。

通过对四川省大渡河沙湾水电站一期围堰塑性混凝土防渗墙应力变形分析［14］，也发现类似的规律。图5-24显示出了围堰中新塑性混凝土防渗墙（双墙方案）的K的取值对新墙应力状态的影响。从中可以看出，随着K值的增加，墙体下游侧的最大压应力（σ1max）明显增大，最大增大幅度达26.5%；墙体上游侧的最大拉应力（σ3min）更是明显增大，最大增大幅度达190%。

上述研究均侧重于对邓肯·张模型参数进行敏感性分析。如前所述，Goodman模型参数对计算结果的精度也有重要影响，所以对这类模型参数的敏感性分析显得同样重要。

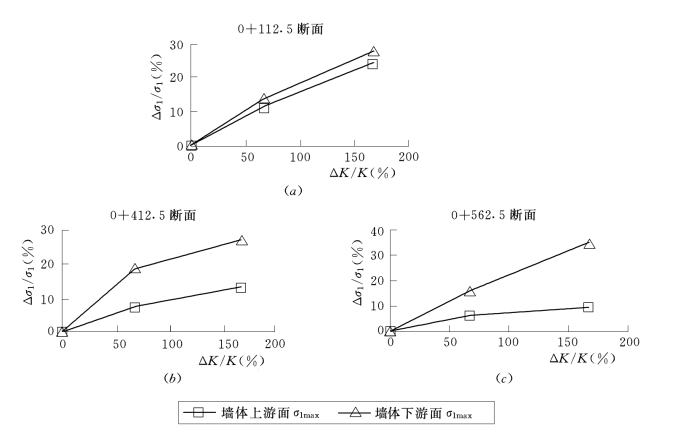
图5-23　横泉水库大坝塑性混凝土防渗墙Δσ1/σ1—ΔK/K关系曲线

河海大学的陈剑博士［15］较为系统地研究了防渗墙接触面参数的变化对应力变形计算结果的影响。文中以伊朗的塔里干黏土心墙堆石坝为例，通过三维非线性有限元计算分析了不同的Goodman接触面模型参数Rf1、K1、n1、δ对应力变形的敏感性。

该研究表明，对于大坝竣工期、正常蓄水期和非常洪水期三种典型工况，接触面的参数变化对于防渗墙的位移影响较小。当参数的变化范围控制在±25%以内时，防渗墙位移的变化范围小于±5%，当参数的变化范围达到±50%时，防渗墙位移有增大的趋势，但其变化幅值仍控制在±10%左右。

该研究同时表明，在大坝竣工期，接触面参数对防渗墙应力的影响也是不明显的，其应力幅值小于±5%。但对于正常蓄水期和非常洪水期两种工况，防渗墙应力随接触面参数的变化非常明显，当参数的变化范围在±10%～±25%内时，防渗墙的应力幅值达到最大值，接近20%。并且注意到，参数n1、δ的变化是单峰值的，而参数Rf1、K1的变化是双峰值的，因此从这个意义上来讲，参数n1、δ作为接触面材料的强度参数的意义更为明显。

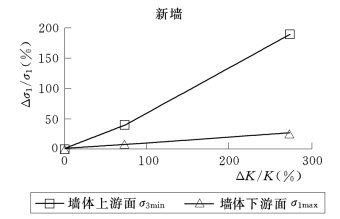
图5-24　沙湾水电站一期围堰防渗墙Δσ/σ—ΔK/K关系曲线

综合来讲，参数K1对计算结果的影响最为显著，其对应力的影响幅值常接近±30%，因此相对而言，参数K1的合理取值相对重要。参数Rf1的影响也很明显，当取值超出0.70～0.90之间时，应力位移结果明显偏于不合理，因此，应对Rf1的取值范围加以限定。当参数n1、δ在合理的取值范围内取大值时，墙体的应力变形对此并不敏感；只有当n1、δ的取值偏小时，墙体才产生较大的应力和位移，且幅值也较大，接近20%。各参数对应力和位移计算结果的影响见图5-25至图5-28。

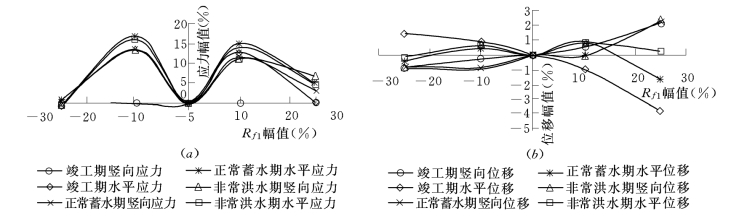
图5-25　Rf1对应力和位移的影响

（a）Rf1对应力的影响；（b）Rf1对位移的影响

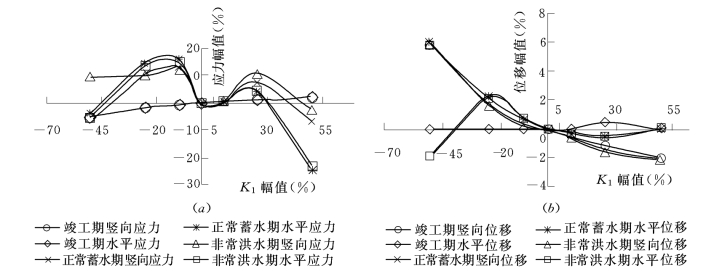
图5-26　K1对应力和位移的影响

（a）K1对应力的影响；（b）K1对位移的影响

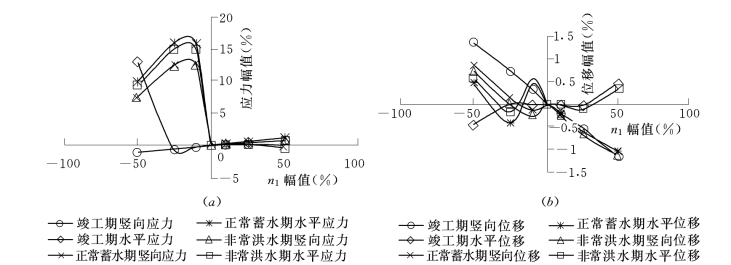
图5-27　n1对应力和位移的影响

（a）n1对应力的影响；（b）n1对位移的影响

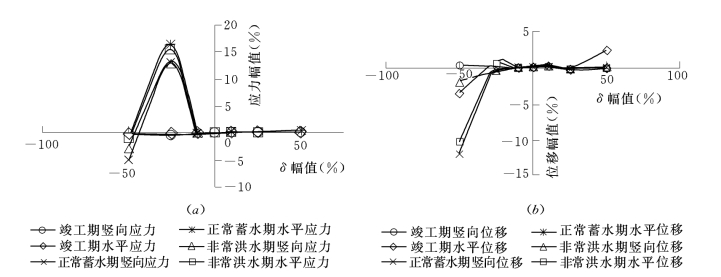
图5-28　δ对应力和位移的影响

（a）δ对应力的影响；（b）δ对位移的影响