混凝土防渗墙是坝基、坝体的处理的工程措施，是坝体（堰体）的重要组成部分，因此，其渗流计算是与坝体（堰体）一起计算的。渗流计算的目的是：确定坝体或围堰的浸润线及下游逸出点位置，以为坝坡稳定、坝体及防渗墙应力变形分析提供资料。确定渗流的水力梯度、局部渗透比降、验算发生渗透破坏的可能性，以便采取必要的措施，保证渗透稳定。计算坝体和坝基的渗流量，估算渗漏损失，以确定设置防渗设施的必要性和设置防渗设施后的效果及确定坝体排水尺寸。

包括防渗墙在内的土石坝（堰）体的渗流计算是一个空间问题，理论计算非常复杂，一般工程上将其简化为平面问题近似求解。随着计算机技术的发展，三维数值计算的方法在重要工程中也得到应用。用平面近似求解时先沿坝轴线选几个变化较大的断面分别进行计算，然后分段叠加计算即为总的渗流量。选择断面注意选择坝基覆盖层、坝体材料以及坝高、墙深等变化较大的断面，以尽量精确计算渗流量。一般来说，防渗墙最深的断面是必须计算的。

渗流分析方法有流体力学法、水力学法、图解法和试验法，工程上最常用的是水力学法。

1.流体力学法

流体力学法是渗流分析的解析法。该法的基本假定是：渗流处于层流状态，服从达西定律

式中　Q——渗流量；

A——土中渗流流断面面积；

K——土的渗透系数；

J——水力坡降。

根据达西定律和渗流的连续方程所得的微分方程为

式中　kx、ky、kz——沿x、y、z方向上的渗透系数；

h——渗流区的测压管水头；

Ss——单位水量，即单位体积的饱和土体在下降单位水头时，由于土体压缩所释放出来的水量。

在工程实际中，一般只考虑各项同性的平面恒定渗流（kx=ky），且不考虑土体的压缩性（Ss=0），则式（4-2）变为方程

式中　Φ——流速势函数，Φ=-kh。

结合土石坝渗流区域的边界条件求解式（4-3）或式（4-4），就可求出流速势函数Φ和浸润线的位置。并由Φ求出任一点的渗透要素。也可根据所得的流速势函数求出其共轭函数，并分别求出相互正交的等值线——等势线和流线，得到土石坝的流网，然后根据流网确定渗透要素。不透水边界、自由面及流线等压线上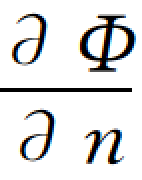=0，n为边界的法线方向。等势面上，Φ=常数。

这种解析解只有在边界条件简单的少数情况下才能得到。在实际工程中，由于土石坝与坝基的边界条件复杂，求解析解通常采用差分法或有限单元法进行数值解。(www.daowen.com)

2.水力学法

土石坝渗流区域大部分范围内流线较平缓，属于缓变流，基本符合达西定律和杜平假定。杜平假定为：坝体土料为均质，各向同性；渗流为缓变流，渗流场中任一铅直上各点的流速和测压管水头是常数。用铅直线代替其等势线，即认为铅直线上各点的流速和测压管水头都是常数。用下列二式分别求出其单宽渗流量与浸润线

式中　q——单宽渗流量；

K——土料的渗透系数；

H1、H2——上、下游浸润线的垂直高度；

L——上、下游浸润线之间的水平距离；

x、y——浸润线上任意点的横坐标和纵坐标。

应用该种方法解土石坝渗流问题，常用等势线或铅直线将土坝横剖面划分成数段，利用各段渗流量相等的条件联立求解。

水力学法是土石坝渗流分析的近似方法。它只适用于平面渗流，由于对流线和渗流场的边界条件作了简化，这能得出渗流区域内的平均渗流要素及浸润线的位置。其解答的精度，一般能满足实际工程的要求，因此应用较为广泛。

3.流网法

流网法求解渗流计算分为手绘流网法和水电比拟法两种。

手绘流网法是根据渗流区域的边界条件，首先确定边界流线和边界等势线，并初拟浸润线，然后按照流网特性用手勾绘并反复修改成正确的流网，以代替在流体力学法中用解析法解拉普拉斯方程所得的流网，最后根据所绘制的流网求渗流要素。手绘流网法可以解决计算方法不易解决的边界复杂的渗流问题，其精确度可达到误差在5%以内。

水电比拟法是用导电材料和绝缘材料将渗流区按一定比例缩制成电流区域模型，并保持电场与渗流场几何相似和边界条件相似，通过测定电场中的等电位线可以得到渗流中的等势线（或流线），然后加绘流线（或等势线），从而得到流网。

4.实验法

根据相似原理，按一定比例将渗流区域缩制成模型。对模型加以观测，然后推算到实际流场。实验法可以分为两类：一类是用土壤、岩石等为介质，在其中发生的仍为渗流，如渗流槽等；另一类是用比拟模型来比拟渗流，其介质已不是孔隙介质，如电比拟法、热比拟法等。该法既可以解决平面问题，也可以解决土石坝空间渗流问题。

各种渗流分析方法，需要根据工程等级、地质条件、设计阶段以及渗流问题的复杂程度等因素酌情选用。一般可采用水力学法；对重要的大坝、高坝或必须按空间渗流考虑的问题，则采用精确的数值计算或实验法验证。