（一）册田水库防渗墙在地震荷载作用下的应力对比分析

为研究混凝土防渗墙在地震作用下的性能，我们对图3-78所示的册田水库防渗墙在7度地震作用下的性能进行了动力有限元分析。

分析采用直接逐步积分法，求解在迁安地震（1976年8月9日）波形（见图3-85及表3-54）作用下的地震应力，计算步长为0.01s，同时考虑了水平地震和垂直地震的作用。并考虑了墙周围土体材料为线性和非线性两种情况。计算参数见表3-55。

图3-85　迁安地震加速波形图

表3-54　迁安地震加速度记录主要参数

在图3-86和图3-87中给出了线性和非线性两种计算方法所得到的墙体地震动应力结果。从中可以看到，对于刚性墙，由于周围土体条件的变化，在坝体与基础亚砂土，亚砂土与风化玄武岩，风化玄武岩与玄武岩的交界部位均产生较大的应力变化，尤其突出的是由于防渗墙插入未风化玄武岩中达2.2m，类似于刚性嵌固，同时其上面的风化玄武岩的弹性模量很低，上下岩层刚度相差很大，从而在水平惯性力作用下，在风化玄武岩中发生了较大的动应力，上游面达到1.19MPa（单元上游边最大垂直向正应力，下同），下游面达到0.96MPa。这一分布规律与静应力的分布规律是相似的。同时，剪应力的最大值发生在防渗墙底部玄武岩层内，最大值为0.50MPa，与静应力发生在同一部位，值得注意。

表3-55　计算模型材料参数表

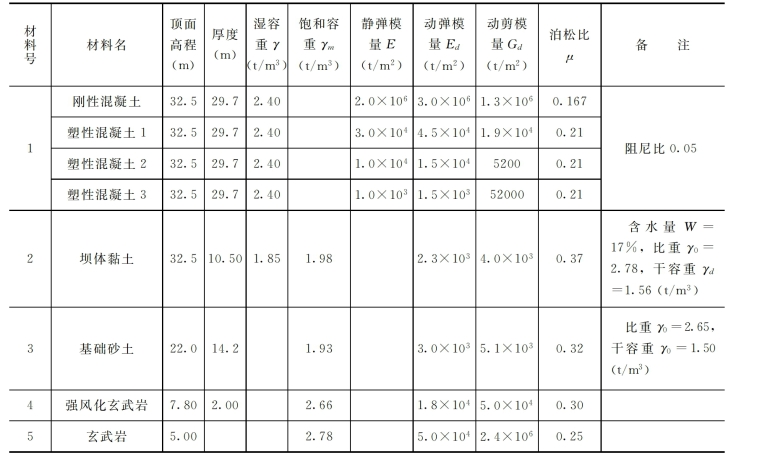
注　表中单位换算：1t/m2=10-2MPa，1t/m3=10kN/m3。

图3-86　刚性混凝土防渗墙地震应力包线图

图3-87　塑性混凝土防渗墙地震应力包线图

对于塑性混凝土防渗墙，由图3-87可以看到，其竖向正应力无论是沿墙高的分布还是其动应力数值均随塑性混凝土的弹性模量而变化，当E=10000MPa时，其应力分布规律与刚性墙相似，应力的最大值仍发生在风化玄武岩中，但最大应力的数值，却比刚性墙小了近9倍，仅为0.138MPa（墙上游面应力）。随着弹性模量E的减小，应力沿着墙高的分布趋于均匀，最大应力的数值也随E而直线下降，当E降到100MPa时，应力数值降低到0.023MPa，仅为刚性墙最大应力的2%左右。

以上说明，塑性墙更能适应地基变形，当E＜300MPa时，最大地震动应力不超过0.05MPa，而刚性墙则达到1.2MPa。

将上述计算得到的地震动应力与静应力计算结果进行叠加，即可得到防渗墙在7度地震时的总的结构应力，图3-88和图3-89给出了叠加后σy沿墙高的分布。叠加中地震应力是按直线考虑土体非线性性质的方法的结果。静应力是按第二种计算情况。

由于地震波的方向是随机的，地震应力的数值既可能是拉应力，也可能是压应力。因此在叠加时考虑了拉压两种情况，可以看到，对于刚性墙，由于地震应力的最不利部位（风化玄武岩层内）与静应力的相同，使上游面的最大拉应力增加17%，达到了5.92MPa；下游面最大压应力增加12%，达到6.75MPa，下游面上部的拉应力达到1.9MPa。此外，最大剪应力达到0.88MPa。

对于塑性墙，由于地震应力的幅值很小，正应力最大不超过0.03MPa，剪应力最大不超过0.05MPa，与静应力叠加后仍然不产生不利的拉应力，如发生8度地震，以最不利的线性计算结果考虑，地震应力增加一倍，塑性墙仍然不会产生不利的拉应力，充分说明塑性混凝土防渗墙的抗震性能是好的。

（二）深基防渗墙在地震作用下应力对比分析［24］

1.原始计算条件及计算方法

图3-88　刚性混凝土防渗墙动静应力叠加图

图3-89　塑性混凝土防渗墙动静应力叠加图

（1）计算对象。本计算以H=60m深的垂直混凝土防渗墙及围土系统为研究对象，所取边界水平宽度L=7H=420m。其网格图如3-90所示。共划分136个单元（其中，防渗墙墙体四边形等参元20个，墙与土接触面分20个无厚度接触面单元，其余为土体单元），147个结点。上下游水面线均与地面重合。之所以选取这样的计算对象，是因下述考虑：

首先，因其具有一定的代表性。这样的模型除了能代表建有防渗墙的天然场地外，还可以模拟斜墙下的防渗墙以及土石坝基础处理完毕而尚未填筑坝体的工况；另外对于防渗墙作为土石坝坝体防渗或坝体补强防渗的情况，由于坝坡较缓，此种模型仍能说明一定的问题。

图3-90　计算网格

其次，能反映墙土联合作用的基本特性。虽然忽略了上部荷重、水头等作用，但是，此模型仍然可以反映墙土系统自振特性的基本性质和墙土相互作用的基本规律。这样使我们的分析更加明确、简单，主要矛盾更加突出。

再就是节省机时和费用。采用这种简化模型，可以大量地节省计算工作量和计算费用。

（2）计算模型及参数。计算中，覆盖层砂卵石、防渗墙塑性混凝土的静力模型均采用邓肯E—μ非线性模型，防渗墙的刚性混凝土采用线弹性模型，混凝土与土的接触面采用刚塑性力学模型。它们的静力参数见表3-56。砂卵石动力特性常数K2=120，动模量与剪应变G/G0—γ曲线和阻尼与剪应变D—γ曲线如图3-91所示；塑性混凝土的动力变形特性见本章第一节，假定其阻尼比D=0.05，不随动应变而变化（研究表明，这样的假定对计算结果影响很小）；刚性混凝土的动力特性按线弹性处理，动弹模为静模的1.5倍，E=21000MPa，阻尼比为0.05。

表3-56　静力参数

注　Kw根据研究需要取700或7000、70000。

作为确定材料动力初始参数的静力计算部分，分两个施工期，第一期为基础覆盖层，第二期修建防渗墙，每一期均分为6次微增量加载。在静力计算的基础上，计算了系统的自振频率（和动力响应）。首先研究了土层本身的自振频率，其次研究防渗墙本身的自振频率，最后研究了墙与围土系统的自振特性。本书仅研究动力反应，未收集自振频率研究成果。

（3）有限元计算程序。动力计算是采用FEASSI程序，该程序是在QUAD-4的基础改编而成的。它以THEPD程序进行静力计算，为动力计算提供初始条件。

（4）地震荷载。与册田水库防渗墙不同，未采用实际地震波形。但为了更明确地研究地震荷载的振幅、频率等特性对塑性墙动力响应的影响，以及更便于分析其互相作用，本文采用简谐波形的人工地震作为动荷即令地震加速度为

图3-91　砂卵石动力特性曲线

式中　Ae——振幅即地震最大加速度；

Te——地震周期。

（5）边界约束条件。本计算研究了三种不同约束情况：①给定水平约束，垂直自由，简称水平约束；②给定垂直约束，水平自由，简称垂直约束；③水平、垂直均自由，称自由约束。

（6）计算方案。为研究不同参数的塑性混凝土及刚性混凝土防渗墙与围土在多种不同地震作用下的动力相互作用，选定了如表3-57所示的计算方案。

表3-57　动力计算基本方案

注　1.g为重力加速度，1g=9.81m/s2；下同。
2.K、n为邓肯模型参数，静初始弹模Ei=K·Pa（σ3/Pa）n。其中，σ3为围压；Pa为标准大气压。KW、KS中下标W、S分别表示墙体混凝土和围土。下同。

2.计算成果分析

计算成果见表3-58。以下将对位移和动应力响应分别进行分析。

（1）水平地震作用下防渗墙与围土的位移响应分析。水平地震作用下塑性墙与围土系统的位移响应的基本特征可用图3-92来表示，该图绘出了塑性墙（KW=7000，n=0.0）及围土（KS=700）在水平地震（Ae=0.4g，Te=0.2s）作用下的位移最大值、最大位移出现瞬时的位移沿墙高的分布等。

从图3-92上可以看出，在墙土系统的位移响应中，垂直位移所占的比重很小，最大垂直位移（Dy=0.0026m）仅为最大水平位移（Dx=0.0216m）的1.2%，因此，在水平地震作用下，塑性墙与围土（或无墙的土层）主要在水平方向上产生变位，即振型是水平剪切型的。因此以下主要讨论水平位移响应。

可以看到，水平位移包线（时程最大值连线）的分布以墙顶及土层表面为最大，往下逐渐减小。而且位移包线和瞬时位移分布是有明显的不同的，这说明由于波的传播墙土系统各处的最大位移响应是不同步的。

图3-92的水平位移包线和瞬时变形曲线均表明塑性墙与附近的土体的位移响应是完全一致的，表明了塑性墙与周围土体的变形是协调的。

表3-58　防渗墙与围土的动力响应

图3-93中给出了在水平地震（Ae=0.1g，Te=0.81s）和垂直地震（Ae=0.15g，Te=0.2s）作用下刚性墙与围土系统中的墙体与围土最大垂直位移沿墙高分布的比较，该图表明，墙土之间的相对滑动主要发生在顶部0.2H范围之内，墙顶部差别最大，在水平地震时，最大垂直位移差为0.23cm，垂直地震时，最大位移差为0.19cm。这种滑动破坏了结构的完整性，同时因为它是动位移，又多发生在静位移稳定之后，其部位又恰在防渗墙顶端与其他防渗体（斜墙、心墙等）的接头部位，因而应给予充分重视。

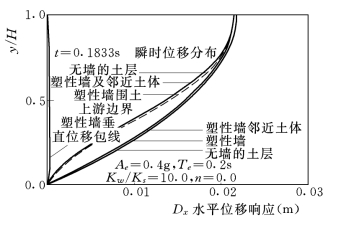
图3-92　塑性墙在水平地震作用下的位移响应

（2）防渗墙刚度KW、Fe对位移响应的影响。从表3-58可以看到，塑性墙与无墙的土层的位移响应相差甚微。但是，相比之下，塑性墙的变位更接近于无墙的土层的变位。这一方面再次表明塑性墙可以适应土层的变形，另一方面也说明防渗墙的刚度对位移响应的影响不甚明显。还可以看出，防渗墙及土层的位移响应主要取决于地震特性、地震频率Fe的改变。(www.daowen.com)

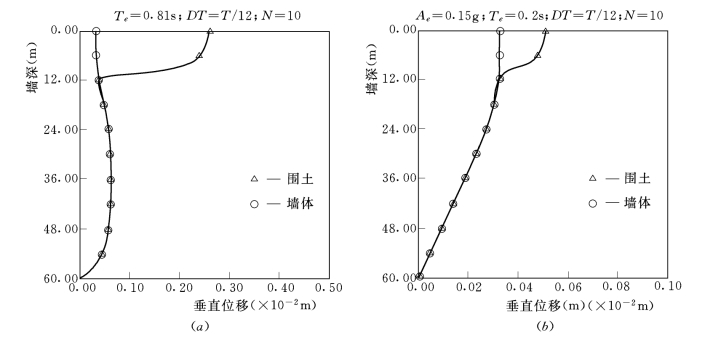
图3-93　刚性墙与围土垂直最大位移比较

（a）水平地震；（b）垂直地震

刚性墙与围土的变形不能协调，其原因归结于刚性墙的模量远远高于围土的（KW/KS=200～300）。在地震作用下，围土的动弹模G随应变发展而降低，而刚性混凝土的G却基本不变，从而造成围土与刚性墙的动模量差距的加大，而且地震愈强烈，这种差距愈大。例如，在Ae=0.1，Te=0.2的水平地震作用下，刚性墙的模量（GW=8974MPa）是围土平均模量（GS=49.8MPa）的36倍，而在Ae=0.4g时（Te保持不变），GW/GS=8974/165.3=54。

而对于塑性混凝土，由于它同围土一样具有动力非线性，使得在地震作用下塑性墙的动模量GW随动应变降低而与围土的模量较为接近，而且地震愈强烈，两者之间差距愈小。例如在Ae=0.1g，Te=0.1s水平地震作用下，塑性墙（KW=7000）与围土的动模量比为GW/GS=13.1；而当Ae增大到0.4时，GW/GS降为6.8，几乎降低了一半。这样，使塑性混凝土与围土的变形更加协调，从而改善了墙体的应力状态，所以塑性墙具有良好的抗震安全性，从而保证了防渗功能的发挥。

（3）应变响应的分析。表3-58给出了各种情况下土体和防渗墙的平均模量G、GW，土体平均剪应变以及土墙系统的初始自振频率F0和其最低自振频率Fmin。同时在图3-94、图3-95和图3-96中给出了γS、GS、Fmin随地震频率Fe的变化曲线。

图3-94　γS—Fe/F0关系曲线

图3-95　GS—Fe/F0关系曲线

从中可以看出，地震特性（Ae、Fe）对防渗墙围土的动应变响应的影响很大。随着Ae的增大，Fe/F0的减小，动应变响应γS有显著的增大，而土体平均模量GS有明显的降低，因而系统的Fmin也显著降低。

根据表3-58中给出的土层平均剪应变γS和墙土系统的最低自振频率Fmin，在图3-97中绘出了各种情况下Fmin—γS的关系曲线。可以看到两者相关关系很好，Fmin随γS值的对数的增加而线性递减。这一关系说明系统的Fmin直接反映了土层γS的动力响应的大小，既反映了地震荷载的加速度Ae的影响，也反映了地震频率特性Fe的影响，Fmin越低，说明地震的作用越强烈，更确切地说，可以用墙土系统的初始自振频F0与其最低自振频率Fmin的比值F0/Fmin来衡量地震作用的强烈程度，F0/Fmin愈大，地震的作用愈强烈。

由图3-96和图3-97还可以看出，塑性墙与围土系统的Fmin与无墙的土层的值极为接近，而刚性墙与围土系统的Fmin则稍低于前两者，说明刚性墙与围土系统的动力响应略为强烈。但防渗墙的刚度对墙土系统最低自振频率Fmin的影响是比较小的。

（4）水平地震作用下应力响应分析。这部分内容是动力响应的重点。图3-98是塑性墙（KW=7000，n=0.0）及围土和无墙土层在水平地震（Ae=0.1g，Te=0.2s）作用下动剪应力在最大τxy出现瞬时的分布情况，可以看到，防渗墙的剪应力响应大于围土及无墙的土层，但三者的分布规律大体相同。而防渗墙附近土体和上游边界处的土体（距墙3.5H）以及无墙的土层中，剪应力的分布基本一致，说明塑性墙的存在对土层剪应力分布影响是不大的。

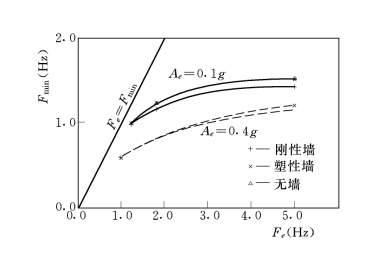
图3-96　Fmin—Fe关系曲线

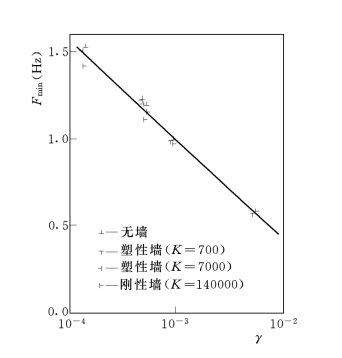
图3-97　Fmin—γS关系曲线

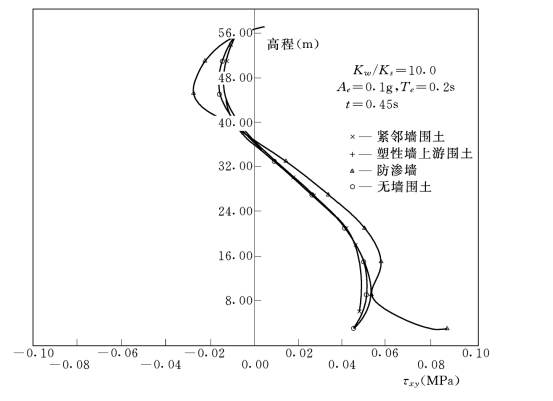
图3-98　塑性墙及围土τxy的瞬时分布

但是塑性墙的存在却改变了周围土层的受力状态，表现为防渗墙附近的土体中动应力σx和σy有了较明显的增长。例如，Ae=-0.1g，Te=0.81s的水平地震作用下，无墙的土层中σx和σy只占很小的比重（见表3-59），土体几乎处于纯剪应力状态；而塑性墙附近的土体及塑性墙墙体中，σx和σy占有了一定的比例，使围土处于较复杂的应力状态。可以看出防渗墙的存在使σx和σy增大，但影响范围不大，剪应力仍是主要的。

考察塑性墙（KW=7000，n=0）墙体的应力分量（σx、σy和τxy）的最大值（见表3-60），可以看出，τxy＞σy＞σx，且三个应力分量几乎依次相差一个数量级。因此水平地震作用下，和土层的应力相类似，塑性墙的剪应力是最重要的应力分量，剪切振型占主导地位。

表3-59　应力状态比较

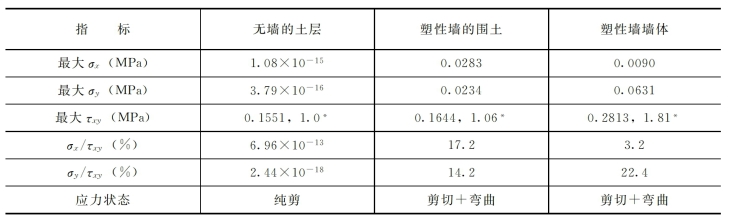
*　表示有塑性墙与无墙土层τxy的比较值。

表3-60　塑性墙应力分量最大值比较

图3-99给出了不同情况下墙体最大应力σy、τxy与F0/Fmin的关系曲线。由图3-99可见，随着F0/Fmin的增加亦即随着地震作用的加强，σy和τxy几乎同步增长。但σy/τxy始终不超过30%，使塑性墙的应力状态基本上以剪切为主，由于垂直正应力很小，因而应尽量提高塑性混凝土的抗剪强度。

表3-61列出塑性墙与刚性墙在F0/Fmin变化时的动应力大小及其比值，从中可以看出刚性墙的σy分别比塑性墙大4.64～17.5倍，刚性墙的剪应力τxy分别比塑性墙大2.48～5.75倍，而且随着墙上系统初始自振频率F0与它们的最低频率Fmin的比值F0/Fmin的增大而增大。这充分表明塑性墙的抗震性明显优于刚性墙。

表3-61　两种防渗墙动应力比较表

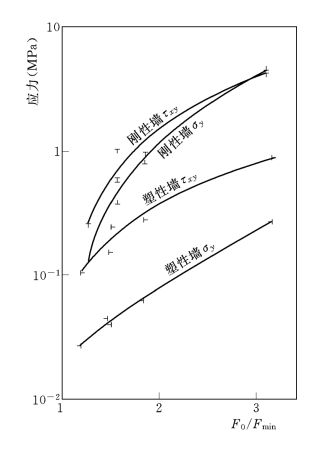
图3-99　防渗墙最大应力与Fe/Fmin的关系曲线

图3-100　防渗墙最大应力与Fe/Fmin的关系曲线

图3-100绘出了各种情况下墙体最大应力σy和τxy与Fe/Fmin关系曲线，该曲线说明了地震频率对墙土系统的应力响应的影响，称为最低频率响应曲线。从图3-100上可以看到，刚性墙的应力大大地超过了塑性墙的应力。具体比较见表3-62。

表3-62　刚、塑性墙地震应力随地震振幅变化比较

刚性墙的应力大大高于塑性墙的应力，是由于刚性混凝土极高的变形模量和围土变形的不协调所引起的。

图3-101给出了地震作用下刚性墙与塑性墙最大应力的比值σyr/σyp、τr/τp与动剪模量比值Gwr/Gwp之间的关系。（脚标r、p分别代表刚性和塑性）。可以看到，由于刚性混凝土与塑性混凝土模量的差别，对剪应力τr/τy影响较小，其比值由2.49增加到4.86倍；而对刚性墙的最大垂直正应力σy有很大影响，使σyr/σyp由4.57倍增长到16.46倍随Gwr/Gwp的增大而增加，实际上Gwr/Gwp的比值一般还要大。而Gwr/Gwp与Fe/Fmin的关系如图3-102所示，即地震愈强烈，Fe/Fmin愈大，Gwr/Gwp愈大，刚性墙的垂直正应力愈大，其值可超过剪应力的数值，使σy/τxy达到1.05，使刚性墙的应力状态变为以弯曲为主的受力状态，这种既有弯曲应力又有很大剪切应力的状态会使刚性墙底部上下游面产生很大的地震拉应力和剪应力，再和静应力叠加，在高水头作用下，上游面有可能出现不利的拉应力，下游面可能出现很大的压应力，同时剪应力也很大，因此使刚性墙的底部产生十分不利的应力状态。

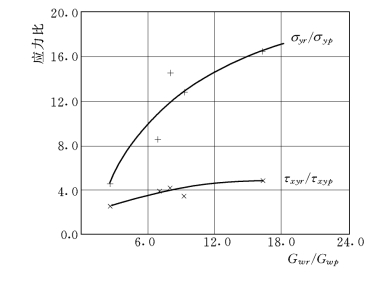
图3-101　应力比σyr/σyp、τxyr/τxyp与Gwr/Gwp关系曲线

图3-102　模量比与频率比关系曲线

（5）垂直地震作用下墙土系统响应的特点。在垂直地震作用下，墙土系统主要发生垂直方向上的运动和变位。以Ae=0.15g，Te=0.2s的垂直地震作用下的情况为例，塑性墙（KW=7000）的最大垂直位移为Dy=0.0058m，而水平方向上没有变位。防渗墙的垂直最大位移沿高程的分布如图3-103所示，最大位移出现在墙的顶部及土层表面，随深度的增加，垂直位移逐渐减少。从该图也可以看出，塑性墙与附近土体的变位是协调的。

塑性墙与附近土体的垂直最大加速度沿高程的分布如图3-104所示。可以看出，其最大的加速度响应出现在防渗墙顶部及土层表面，而且塑性墙与邻近土体的加速度响应也是一致的，再次说明了塑性墙与围土的运动一致，变形协调。

垂直地震作用下，墙土系统运动方向的改变（即垂直振型占主导地位，与水平地震时不同），必然带来应力响应的差别。本例中，塑性墙的最大σy=0.2922MPa，最大τxy=4.921×10-3MPa，显然，此时的塑性墙处在单纯的拉压应力状态，这和土层的应力状态是一致的。塑性墙及邻近土体中σy最大值沿高程的分布如图3-105所示，可以看出，墙体及邻近土体的应力分布的形状相似，且比较均匀，在底部取得最大值；塑性墙应力高于土体。

由此看出，地震方向的改变使得防渗墙与围土系统的动力响应中主振型发生了显著的变化，从而也改变了防渗墙及围土的应力状态。

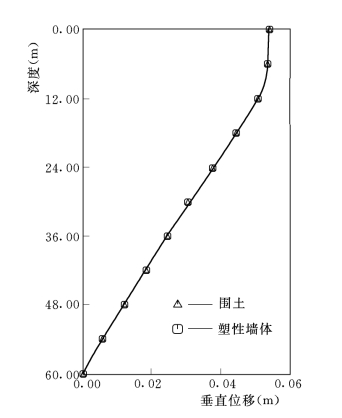
图3-103　垂直位移包线

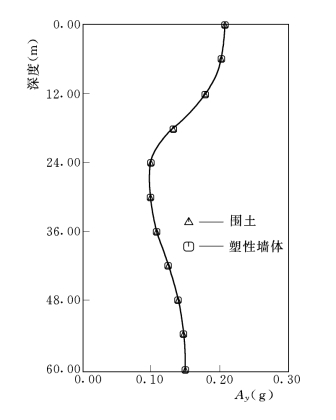
图3-104　垂直加速度包线

3.深基防渗墙地震力响应小结

通过对混凝土防渗墙与围土系统的动力相互作用的研究，以及与刚塑性墙的对比分析，得到以下主要结论：

（1）墙土系统的动力响应主要由土层的动力特性和地震动荷的特性决定，塑性混凝土防渗墙除动弹模KW外的材料参数对墙土系统整体动力响应没有显著影响。

（2）墙土系统的最低自振频率Fmin，反映了墙土系统的动力响应激烈的程度，可以用F0/Fmin来标志系统的动力响应，F0/Fmin愈大，动力响应愈强烈。由于地震的Fe越接近Fmin，Fmin就愈低，很难达到Fe=Fmin，因而墙土系统这样的动力非线性系统在地震作用下，较一般线性系统更加不会发生共振的情况。

（3）塑性墙与围土变形协调，应力分布与围土一致，处于剪切应力为主的剪切加弯曲应力状态，应力响应较低。刚性墙与围土的变形不能协调而出现了接触面上的相对滑移，有可能导致渗漏破坏应给予充分重视；其应力分布和数值与围土差别很大，应力响应大大高于塑性墙。塑性墙的抗震性能优于刚性墙的根本原因是它具有动力非线性性质，在地震作用下，塑性混凝土动模量随应变发展而降低。而且地震越强烈，塑性强模量降低的幅度越大，与围土的模量越接近，因而，抗震性能也更加优越。

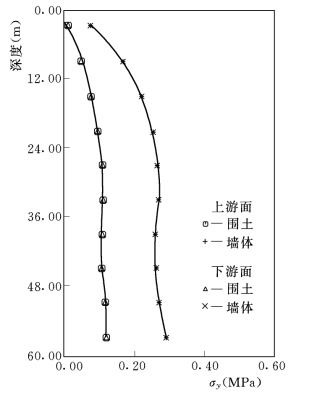
图3-105　动应力包线

（4）垂直地震作用下，动力响应以垂直振型为主，防渗墙与围土均处在单纯的拉压应力状态，这对抗拉强度较低的塑性混凝土是应该重视的。