从对册田水库南副坝防渗加固工程的防渗墙的结构计算结果可知，塑性混凝土防渗墙在7度地震作用引起的地震应力仅占静载引起应力的0.5%，且无拉应力；而刚性墙地震引起的压应力为静应力的12%，拉应力占静应力的17%。这充分表明塑性混凝土防渗墙具有良好的抗震性能，堪称地震区防渗工程的良好结构。为了进行地震区塑性混凝土防渗墙的结构设计，必须确定其动力特性，因此必须进行动力特性试验研究。

（一）动力特性试验方法

由于塑性混凝土是介于土和普通混凝土之间而更接近一般土体的一种材料。目前测定不同剪应变水平的土体的动（剪）弹模和阻尼比的室内试验方法有5种，它们分别是拟静扭剪共振柱试验、振动三轴试验、振动单剪试验、振动扭剪试验和振动台试验。它们各自所能承受的应变水平不完全相同，每种试验只能在各自有限的应变范围内进行，如图3-19所示。

为了测量塑性混凝土在较大应变范围内（γ=10-9～10-2）的动力特性，根据试验条件选择了振动三轴试验和共振柱试验两种方法，前者适应大应变γ≥10-5，后者适应小应变γ≤10-5。

（二）试验设备和试验方法

1.共振柱试验设备和试验方法

塑性混凝土小应变动力特性试验是在美制“拟静扭剪共振柱”仪上进行。仪器的主体部分如图3-20所示。属单自由型，自由端部有集中质量作用。

工作原理是声频信号发生器输出正弦波信号送入功率放大器，经放大后送入激振器，使试样顶部发生强迫振动（扭转性）。调整信号发生器的输出频率，直至系统发生共振，测得共振频率，即可用下述方法计算试样的动剪切模量。切断电源，测电信号的衰减曲线，根据衰减曲线可以用衰减速度计算试样的阻尼比。全部操作和数据采集及整理均由计算机控制。

根据试验结果，并通过下述计算，就可以求得试样的动弹模G，动剪应变幅值γ和阻尼比DT。

图3-17　混凝土折减系数α—f（立方体强度）曲线图

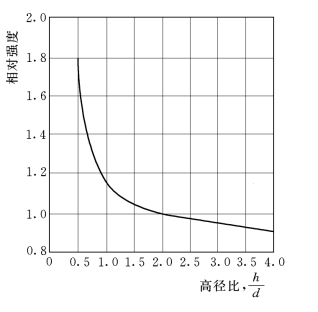
图3-18　高径比对圆柱体试样表观强度影响模式图

图3-19　各种试验方法适用的应变范围［9］

（1）试样的动弹模G。

式中　ρ——试样的密度，kg/cm3；

L——试样的长度，m；

fT——实测的系统的共振频率，Hz；

FT——频率因子，根据系数TT由仪器专用曲线查得。

式中　JA——顶盘系统的极惯性矩，kg·m2；

J——试样的极惯性矩，可以由试样质量和直径算得；

f0T——仪器本身的共振频率，为75.2Hz。

（2）试样的动剪应变幅值γ。

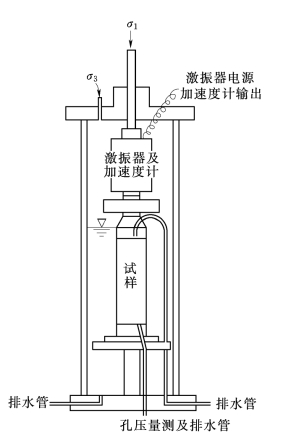
图3-20　拟静扭剪共振柱仪

式中　RCF——扭转运动校正因子，本仪器为4.02/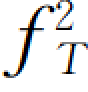，弧度/V（有效值）；

RTO——加速度计输出电压，V（有效值）；

d——试样直径，m；

L——试样长度，m。

（3）试样的阻尼比。

式中　δST——对数衰减率；

n——衰减振动第1周至所取最后一周的周数；

A1——第1周的双幅值；

An+1——第n+1周的双幅值；

ST——能量比；

δT——仪器的对数衰减率，本仪器为0.00678。

2.振动三轴试验设备及试验方法

（1）试验设备。振动三轴试验是在水利水电科学研究院抗震防护研究所的S—3—D动态三轴压缩试验机上进行的。该机器是室内测定动剪模量和液化强度最为常用的试验设备，其装置如图3-21和图3-22所示。

（2）试验方法。试验时，将制备好的圆柱形试样置于压力室之中，轴向荷载P1和动荷载P通过荷载活塞施加，围压由压力室的水压施加。压力和变位信号分别通过设在轴活塞下端部的应变片式轴向压力传感器和设在框架上的差动变压器式轴向变位传感器量测，并与控制柜相连，由控制柜实施控制和监测，并由与之相连的光电示波器或X—Y记录仪记录轴向动应力σ和轴向动应变ε，以及应力应变滞回圈。此试验机的轴压、侧压的动、静态值均可以随意调整和控制，并在数字窗显示。

图3-21　S—3—D动态三轴压缩试验机装置示意图

1—轴向变位传感器位置；2—轴向压力传感器位置

试验机要求试样直径为100mm，而本次试验用的试样为直径71.1mm的实心圆柱体。为了与试验机匹配，我们特地加工了一个试样帽和一个试样底板，用来连接试样和试验机，如图3-22所示。

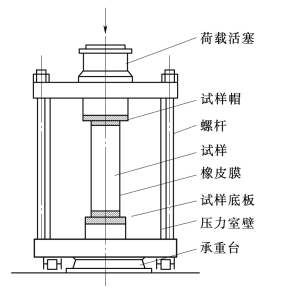
图3-22　S—3—D动态三轴压缩试验机压力室详图

图3-23　荷载传递关系图

（a）动荷载；（b）静荷载

试验时，将试样置于压力室中的试样底板之上，以橡皮膜密封，进行加压固结，待变形稳定后，再对试样施加动荷载。由控制柜施加在活塞上的动荷载p（相应于直径100mm的试样）与本试验所用试样（直径71.1mm）实际承受的动应力σ是不相同的。分析试样帽的受力（见图3-23）可以得到动应力σ与动荷载p之间的转换关系为

其中，Ψ=100mm，φ=71.1mm，所以，p=0.5055σ。所以，当已知动荷载p后，即可确定作用在试样上的动应力σ。

在等压固结时，控制柜施加的静荷载（p1，p3）与试样实际承受的荷载（σ1，σ3）有以下关系：

根据试样帽的受力平衡条件，有

化简得到，σ1=p1，即是试验机所加静荷载强度和试样所受的压应力是相等的。

在本次动三轴试验中，对4组塑性混凝土试样（I5～I8）进行了等压固结情况下的排水振动三轴试验。固结压力σ3=0.1～1.2MPa，在每个固结压力σ3下，对试样施加若干级不同幅值的正弦波形轴向动荷载σ，每级动荷载持续作用10个周期左右，多者达30个周期。试验中加荷次序有σ从小到大、从大到小以及从小到大再到小等几种不同的方式。最大荷载σ一般不大于相应的固结压力σ3。动荷载振动的频率依常规选定为1Hz。

另外，对其中的16组试样还进行了偏压固结（σ1=1.2MPa，σ3=0.8MPa）情况下的动三轴试验（6-1）及破坏试验（6-1和6-2）。

本次试验的应变范围为ε=2.65×10-5～1.08×10-3（γ=3.21×10-5～1.30×10-3），最大动应力达到σ=1.4MPa。

试样周围可以施加等压固结即σ1=σ2=σ3，亦可施加非等压固结即σ1≠σ2=σ3。

由测得的动应力σ和动应变ε，以及它们所形成的滞回圈（见图3-24），根据黏弹性理论，即可求得塑性混凝土的动力特性如下：

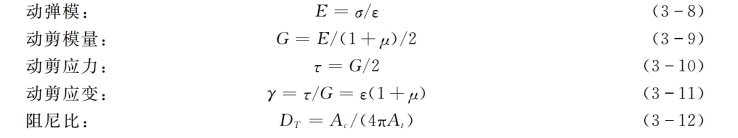
式中　μ——泊松比；

Ac——滞回圈的面积；

At——三角形AOB的面积如图3-24所示。

（三）试样配比及试样尺寸

试验所用试样共8组配比，其中4组为表2-12中的I1、I2、I3、I4，另外4组I5、I6、I7和I8如表3-14所示，后4组配比仅用水量不同，其余原材料是相同的。试样龄期，I1～I4为28d和90d，I5～I8为60d、72d、73d和78d，试样为饱水实心圆柱形，直径为7.11±0.01cm，高19.3±0.08cm。试验时所用围压σ3中，共振柱试验的σ3较小，σ3=0kg/m2、0.5kg/m2、1.0kg/m2、2.0kg/m2、3.0kg/m2；振动三轴试验的σ3较高，σ3=0.1MPa、0.2MPa、0.3MPa、0.4MPa、0.6MPa、0.8MPa、1.0MPa、1.2MPa。

图3-24　理论滞回圈

表3-14　试样基本情况

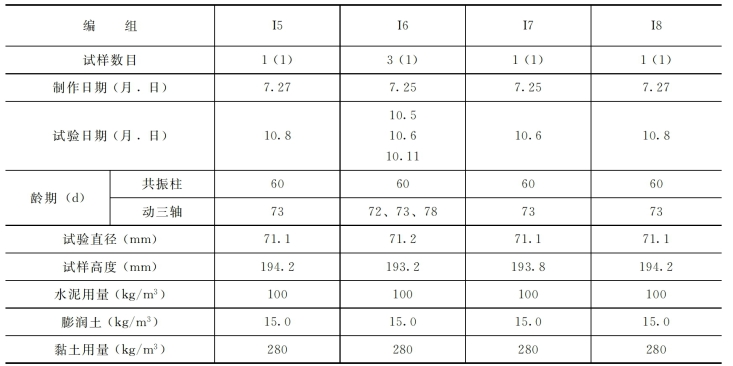
续表

注　1.试样数目一栏中括号内的数字为共振柱试验试样数，括号外数字为振动三轴试验试样数。
2.表中日期均指1990年。

（四）试验结果与分析

众所周知，近代科学技术的发展，使我们可以采用有限单元方法对土工建筑物和防渗墙的组合体进行动力作用（如地震荷载）下的计算，并由此评价其安全性。为此我们需要知道建筑物的动力特性参数，如动模量、阻尼比等，并且需要分析这些动力参数随应变的变化情况。

1.共振柱试验结果(www.daowen.com)

共振柱试验结果示于图3-25～图3-28中，这些曲线均为动剪模量的变化曲线，其中图3-25为剪切模量G随剪应变γ的变化曲线，从中可以看出，曲线较为规律平滑，G随γ的增加略有下降，但受σ3的影响较为明显。

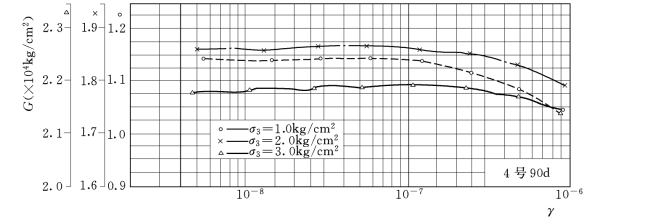
图3-25　典型G—γ曲线图

注　G的单位为kg/cm2（1kg/cm2=0.1MPa）。

图3-26、图3-27和图3-28为I1、I2、I3和I4配比试样的G随σ3的变化。这4个配比仅水泥用量不同，分别为126.7kg/m3、108.6kg/m3、95.0kg/m3、84.4kg/m3，其余材料（包括膨润土、黏土、骨料和水）均是相同的。由图3-26、图3-27和图3-28可知，水泥用量越高，G值越大，其增大幅度几乎与水泥用量同比增大，如G1/G4=1.42，二者水泥用量C1/C4=1.50；σ3越大，G值几乎成直线增大；随着龄期的增长，G值亦成倍增长，如I3在28d龄期时，G28=1.07×104kg/cm2（σ3=2.0kg/cm2）；90d龄期时，G90=1.92×104kg/cm2（σ3=2.0kg/cm2），二者比值为G90/G28=1.79。

图3-26　28d龄期I1、I3、I4 G—σ3曲线图

图3-27　90d龄期I1、I2、I3、I4 G—σ3曲线图

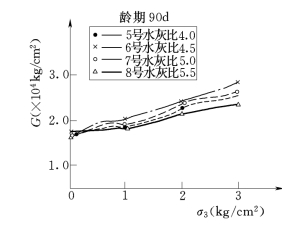
图3-28　90d龄期I5、I6、I7、I8 G—σ3曲线图

图3-28所示4个配比仅水灰比不同，分别为4.0、4.5、5.0、5.5。由图3-28可以看出，除了G随σ3增大而增大以外，G随水灰比增大而减小，但影响不很明显，尤其σ3较小之时。

图3-29表示典型试样的阻尼比DT随γ的变化情况。由图3-29可以看出，在试验应变范围内，DT有随γ的增大而增大的趋势，但不很明显。另外，试验表明，随着龄期的增长，阻尼比明显下降，28d龄期的阻尼比的变化范围为0.035～0.052，而90d龄期的阻尼比的变化范围则降为0.016～0.021。由图3-29还可以看出，随σ3的增大，阻尼比亦下降。

2.振动三轴试验结果

分析振动三轴试验结果主要是从本构关系、动剪模量和阻尼比这三方面着手的，但因试验条件限制，试样数量有限，有些结果尚需进一步充实。

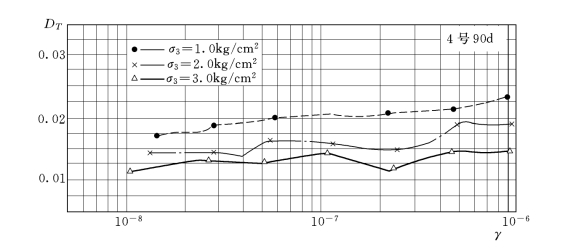
图3-29　典型试样的DT—γ曲线图

振动三轴试验结果如表3-15所示。根据表3-15中的数据求得有关曲线如图3-30～图3-37所示。

表3-15　试验基本情况

续表

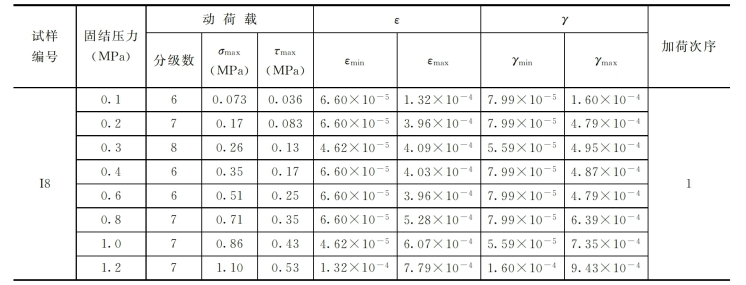
注　1.*表示试样在该状态下发生破坏。
2.加荷次序为：①小—大；②大—小；③大—小—大；④小—大—小。

图3-30　动应力σ和动应变ε关系曲线

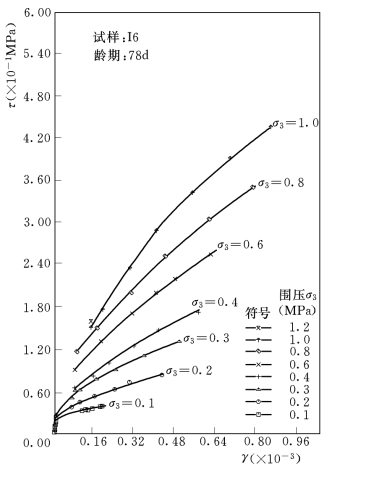
图3-31　动剪应力γ和动剪应变τ关系曲线

（1）振动荷载作用下塑性混凝土的本构关系。图3-30所示为I6试样的动应力和动应变的关系曲线。由图3-30可以看出，塑性混凝土在给定荷载的作用下表现出良好的弹性，也表现出非线性的特性。此外，塑性混凝土的动力特性受围压σ3的影响是非常明显的，其最大动应力σmax随σ3的增长几乎成倍增长。

图3-31表示出了动剪应力和动剪应变的关系曲线。它与图3-30所给出的动应力—动应变关系曲线具有相似的形状，亦具有相同的规律性，即弹性非线性以及受围压σ3的影响明显。这是因为存在τ=σ/2和γ=（1+μ）ε的关系。

图3-32表示出不同配比试样在σ3=1.0MPa的条件下的最大剪应力和相应的剪应变都落在同一条光滑的曲线上，但当σ3不同时，可以得到不同大小但形状相似的曲线，如图3-33所示。

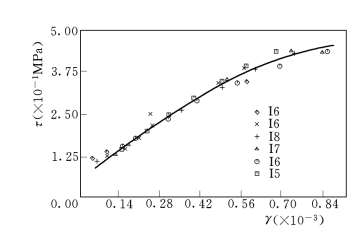
图3-32　不同配比试样最大剪应力和相应剪应变的关系曲线（σ3=1.0MPa）

图3-33　不同σ3作用下最大动剪应力和相应剪应变关系曲线

（2）振动荷载作用下塑性混凝土的剪切模量。图3-34～图3-36表示了动剪模量G的变化规律，为计算塑性混凝土的动剪模量提供了依据和方法。其中，图3-34表示了动剪模量G随剪应变γ的变化规律，表明G随γ的增大而迅速减小，特别当γ较小时（如γ＜0.1×10-3），G值下降更快。此外G值还明显受到围压σ3的影响，σ3越大，G值越大。如表3-16、图3-37和图3-38所示，随着σ3的增大，G（或E）值成倍的增长。而且由图还可以看出，当σ3＜0.6MPa时，G（或E）值增大迅速，而当σ3＞0.6MPa时，G值增大较慢。

表3-16　塑性混凝土动弹模和动剪模量受围压σ3的影响

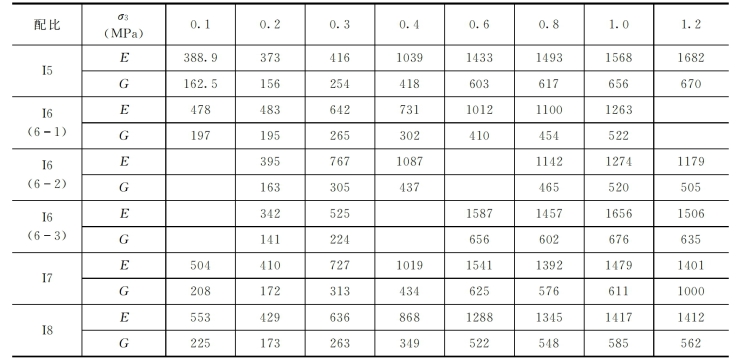
注　表中动模量E=σmax/εmax，动剪模量G=τmax/γmax。

图3-35将共振柱试验的结果和振动三轴试验的结果绘制在同一张图上，从而可以更加全面地反映塑性混凝土试样的动态变形特性。由图3-35可以看出，两种试验曲线可平顺衔接。由图3-35还可以看出：①当γ＜10-5时，动模量G基本不随γ而变化，而当γ＞10-5时，G随γ的增大而迅速降低，这与一般土体的性质相似。据此，我们可以将γ＜10-5时的G称为初（起）始动剪模量，用G0表示。②图中σ3=0.1MPa、0.2MPa、0.3MPa的三条曲线的形状基本相同。如分别给出各个试样的G/G0—γ关系（σ3≤0.3MPa），并点绘在图3-36中（点），可以看出它们的规律是一致的，用最小二乘法原理可以得到归一化的关系式：

图3-34　G—γ关系曲线

图3-35　两种试验的G—γ关系曲线的衔接

图3-36　G/G0—γ关系曲线

本次试验得到的参数A1=0.0834，B1=1.759×10-5，γ0=2×10-5。从图3-35上可以看出，式（3-13）很好地拟合了σ3≤0.3MPa的试验点。

将上述数据代入式（3-13），即得到

图3-37　动剪模量G与围压σ3的关系曲线

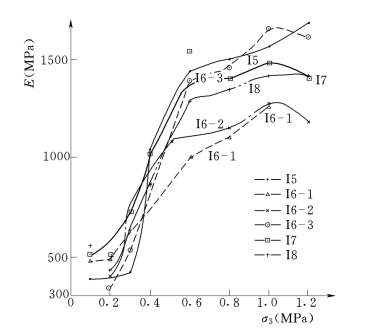
图3-38　动弹模量E与围压σ3的关系曲线

图3-36的概化曲线说明，当σ3≤0.3MPa时，塑性混凝土的动剪模量G/G0随γ的变化关系与σ3无关。而G0却随围压σ3而改变，所以，只要确定了不同围压下的G0，由式（3-13）即可确定在该围压下的G—γ的关系。

如前所述，由图3-38可知，G0随围压的提高而增大，两者之间基本上呈如下线性关系：

其中，A2为σ3=0时的G0值；B2为无量纲参数。对于I5～I8组试样，90d龄期，A2=1.63×103MPa，B2=3262.0。

这样，已知σ3即可由式（3-15）求得G0的值。

又由静力试验表明，静初始模量Ei基本上是不随围压而变化的，而且由静力试验测定Ei值是比较方便的，这样便可以得到G0/Ei与σ3的关系为

其中，A3是σ3=0时G0与Ei的比值，B3也为无量纲参数，Pa为一个标准大气压，Pa=0.10MPa。对于I5～I8四组试样，平均的Ei为780.8MPa，由此可以求得A3=A2/Ei=2.09，B3=B2/（Ei×0.1）=0.42。

于是，若已知试样的静初始模量Ei，即可根据式（3-16）求得某一围压σ3下的初始动剪模量G0，从而得到动剪模量G与动剪应变γ的关系。

以上得出σ3≤0.3MPa情况下求塑性混凝土动剪模量的方法及有关公式，以下提出σ3＞0.2MPa时，求G—γ关系的方法。

为了确定σ3＞0.3MPa时G—γ的关系，不妨假设此时G0与σ3仍满足式（3-15）的直线关系。先用式（3-15）外延求σ3=0.4MPa、0.5MPa、…、1.2MPa时的G0，再将相应的试验点也概化为G/G0与γ的关系，同样点绘在图3-36上（⊙点）。可以看到，这些试验点也很好地符合拟合曲线式（3-13），这表明在不同的σ3下，可以认为均符合式（3-13）的关系。这样，在缺少试验资料的情况下，σ3＞0.3MPa时，动模量与动应变的关系也可近似按式（3-13）所代表的曲线来拟合。这样，式（3-13）～式（3-16）的适用性就更为广泛了。当然，这仅是一种在缺乏试验资料的情况下的近似估算方法，如果条件许可，还是用实际试样进行试验来确定σ3＞0.3MPa时的G—γ关系。

归纳起来，求塑性混凝土的G—γ曲线的步骤如下：

1）根据塑性混凝土的静初始弹性模量Ei，由式（3-16）可以求得某个围压σ3下的G0，亦可由式（3-15），由已知的σ3求出G0值以资比较。

2）当已知G0，就可由式（3-13）确定G—γ的关系曲线。在进行计算时需要先根据试验资料求出上述公式的常数A1、B1、A2、B2、A3、B3。

此外，从以上分析还可以看出，当σ3=0时，G0=1.63×103MPa，若取μ=0.21，则初始动弹模E=2（1+μ）G0=3945MPa，约为静初始模量Ei的5倍。

（3）塑性混凝土试样在动荷载下的破坏。在试验过程中，6-1和6-2两个试样发生了破坏，破坏均发生在较高的围压下，其中6-1号试样试验破坏时围压σ3=σ1=1.2MPa，6-2号试样试验破坏时围压为σ1=1.2MPa，σ3=0.8MPa。两个试样的破坏均发生在卸载的半周并且产生了较大的残余变形（6-1号试样为εp=7×10-4，6-2号试样为εp=2.2×10-2），而在加载半周，试样仍基本上保持了弹性性质。破坏时的应力、应变状态及动荷载作用周次分别如表3-17表示。

表3-17　破坏时的状态

从表3-17可以看出，6-1号和6-2号两试样破坏时的应力、应变状态有很大的差别，然而它们却同样的经历了500周次以上的往复荷载的作用，基本上可以认为是疲劳破坏。由于试样数量较少，未能对破坏现象进行深入的研究，因此，这里的结论只能作为参考。

但是，从表3-17仍可得到塑性混凝土动强度的一些基本认识：三轴应力状态下，塑性混凝土可以经受不少于500周次的动荷的作用，动荷作用时间大于50s，超过一般地震作用的时间，所以，实际工程中塑性混凝土结构发生疲劳破坏的可能性很小。计算表明，在周期为0.2s，最大加速度为0.4g（g为重力加速度）的简谐振动荷载作用下，塑性混凝土墙的最大动应变为γ=3.77×10-4（围压0.35MPa），而本试验中，在0.3MPa围压下，塑性混凝土试样动应变达到4.16×10-4～7.15×10-4而未产生破坏。所以，在地震作用下，塑性混凝土防渗墙具有较大的安全度。

（五）塑性混凝土进行动力试验主要结论

利用动态三轴压缩试验机和共振柱试验，测定了塑性混凝土的主要动力特性，对塑性混凝土动力特性有了较为全面的认识，得到了塑性混凝土的一些基本规律总结如下，但因试验条件所限，下述结论仅供参考。

（1）在一定的围压和固结状态下，在往复荷载作用下，塑性混凝土呈现弹性非线性性质，既没有残余变形产生，又与加载方式无关。这种明显的非线性性质与土的动力特性是相似的。当γ≤2×10-5时，动模量G不随γ而变化，称为初始动剪模量G0；当γ＞2×10-5时，G随γ的增大而急剧减小。G/G0—γ关系可以用式（3-13）表示，并可直接应用于动力计算中。

（2）围压对塑性混凝土的动模量有较明显的影响。G0和σ3之间存在着简单的线性关系可以用式（3-15）表示。

对于本次试验的塑性混凝土而言，可由静初始弹模Ei和围压σ3确定G0，从而确定此围压下的G—γ关系。

（3）塑性混凝土的动模量E与静模量Ei的比值较大，E约为Ei5倍，而普通混凝土的E/Ei一般为1.5。

（4）塑性混凝土可以承受较高的动应变和动应力。本次试验中，塑性混凝土最大动应力达σ=1.4MPa，τ=0.71MPa，最大动应变达ε=1.08×10-3，γ=1.30×10-3。

在往复荷载作用下，塑性混凝土可能会出现疲劳破坏。但是从破坏时的应力、应变状态及动荷作用周次看，在一般地震作用下，塑性混凝土结构一般不会发生疲劳破坏，可以认为塑性混凝土防渗墙的抗震安全度是可以保证的。

（5）在水泥用量相同的情况下，水灰比的变化对塑性混凝土的动力特性的影响不明显。由于仪器条件的限制，本次试验只能得到塑性混凝土在小应变条件下的阻尼特性，这是较为遗憾的；同时，本次试验还缺少σ3＞0.3MPa时的共振柱试验资料（主要是G0）；本次试验的试样数量也较少，对塑性混凝土动强度及破坏特性也未能深入研究。这些问题在今后尚待进一步研究，本次试验结果仅供参考。