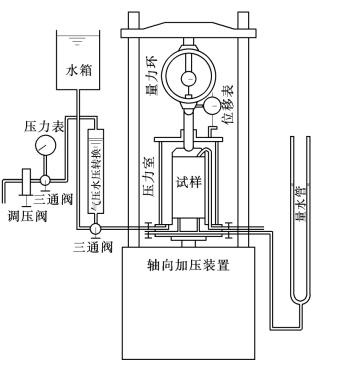
图3-1　三轴试验设备示意图

根据防渗墙的受力特点，对塑性混凝土进行了无侧限压缩试验和三轴压缩试验，用以研究四围压力水平和不同配合比对塑性混凝土力学特性的影响，此外还研究了混凝土的龄期和加载速率的影响。

试验设备的主机为英国进口的WF—10072高压三轴剪力仪，另外配置了四围压力加压设备和排水量测装置，整个试验系统示意图如图3-1所示。无侧限压缩试验加载速率为0.2mm/min，常规三轴排水试验的加载速率为0.02mm/min。

试样为直径150mm、高300mm的圆柱体。室内试样由机器搅拌浆体人工装模成型，2d（夏）～7d（冬）拆模，然后进行标准养护（温度20±3℃，相对湿度大于95%）。现场试验由机口取样，人工装模成型，水中养护。研究所用试样的配比如表2-12所示。

（一）无侧限压缩试验结果及其分析

共对室内41种配比107个试样，现场16种41个试样，共57种148个试样进行了无侧限试验［1，2］。

1.试验结果试样强度qu、初始模量Ei及峰值（极限）应变εaf见表3-1。对其影响因素的分析如图2-2～图2-4所示。

表3-1　塑性混凝土无侧限压缩试验成果汇总

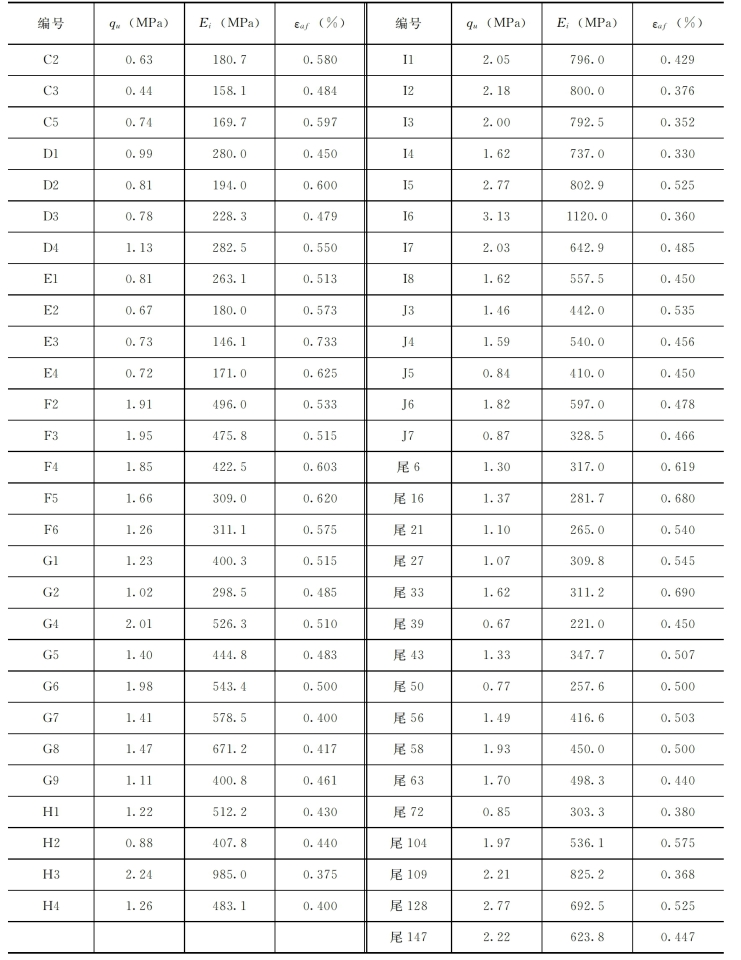
注　C2～J7共41组为表2-12室内配比试样，尾6～尾147共16组为现场试样。

几组典型试样的轴向应力—轴向应变曲线关系如图3-2所示。曲线形态酷似土的应力应变关系曲线。

2.无侧限压缩试验塑性混凝土试样破坏型式

试样的破坏型式主要为压碎型，如图3-3（a）所示；也有剪切破坏型式和压碎剪切混合破坏型，如图3-3（b）和图3-3（c）所示。

3.无侧限试验条件下塑性混凝土初始模量Ei与强度的关系曲线

如图3-4所示，在同一水泥含量的情况下，两者基本上呈直线关系，即强度越大，模量越大。

（二）常规三轴压缩试验结果及其分析

1.三轴压缩试验条件下的破坏型式及塑性混凝土防渗墙设计强度准则

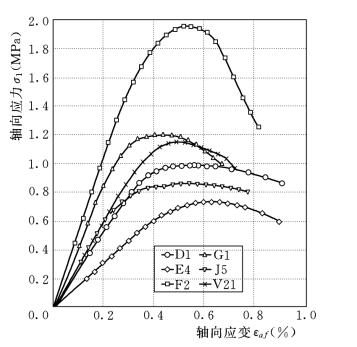
图3-2　典型试样无侧限压缩试验应力应变曲线图

如图3-5所示，塑性混凝土试样在三轴条件下的破坏型式与无侧限条件下有所不同，试样属典型的塑性剪切破坏，破坏时试样上有明显的带状剪切面。

图3-3　无侧限压缩试验试样破坏型式

（a）压碎型；（b）剪切型；（c）混合型；（d）试验前

根据上述特点，应用摩尔—库仑强度准则，即用强度指标黏聚力C和内摩擦角φ来描述塑性混凝土的强度特性是合适的。图3-6为四个试样破坏时的摩尔圆和强度包络线。所进行的塑性混凝土三轴试验得出的C值为0.2～0.8MPa，φ值在25.3°～39.7°范围内变化。

以前设计防渗墙常采用第一强度理论，认为当某一单元最大主应力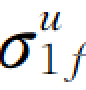达到无侧限强度qu，即该单元达到受压破坏

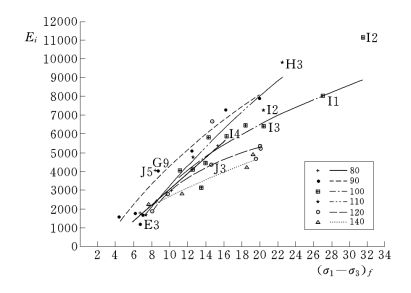
图3-4　模量与强度的关系图

图3-5　三轴压缩试验试样破坏型式——塑性剪切型

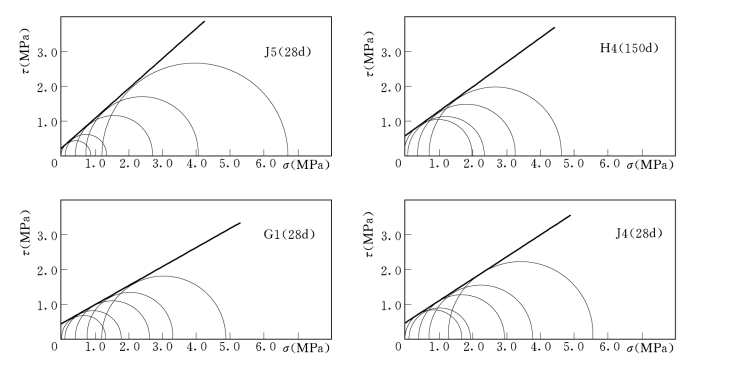
图3-6　三轴试验破坏摩尔圆及强度包络线图

而摩尔—库仑理论认为某单元破坏时的最大主应力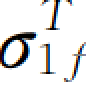为

2.四围压力对塑性混凝土强度和极限应变的影响

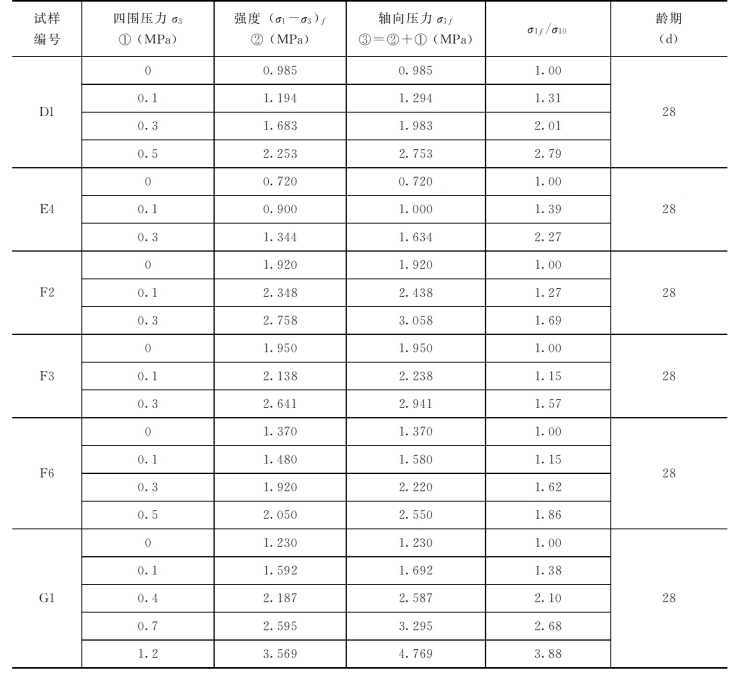
为了探索四围压力对塑性混凝土强度的影响，我们在塑性混凝土三轴试验中，四围压力σ3采用0MPa、0.1MPa、0.4MPa、0.7MPa和1.2MPa，共对13组配比、28d龄期的试样进行了固结排水试验，此外还对龄期分别为90d、120d、150d和385d的试样进行了各一组三轴试验，试验成果如表3-3所示，其（σ1-σ3）—εa—εv曲线如图3-7～图3-10所示，其中σ1—σ3为偏差应力，εa为轴向应变，εv为体应变。

表3-2　两种强度理论最大破坏主应力比值表

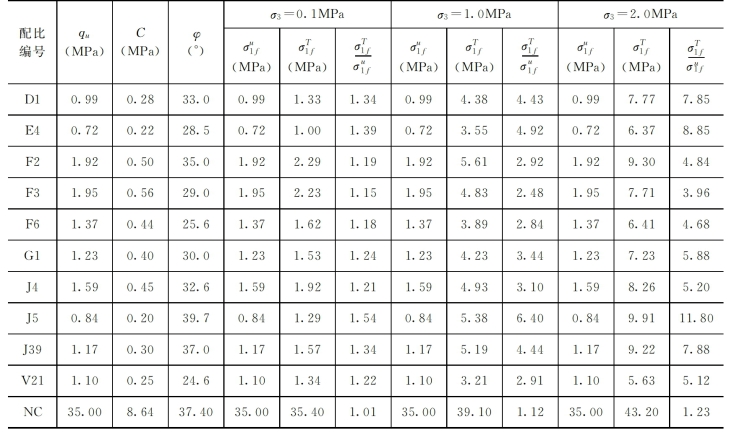
注　NC表示普通混凝土，据姜福田（1989）引用的Richart et al.试验资料。

表3-3　塑性混凝土三轴试验成果表

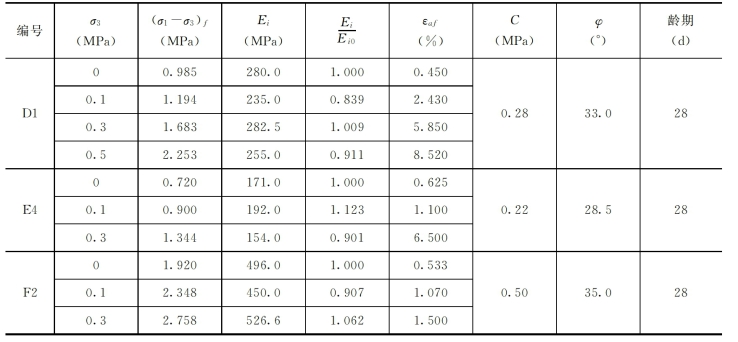
续表

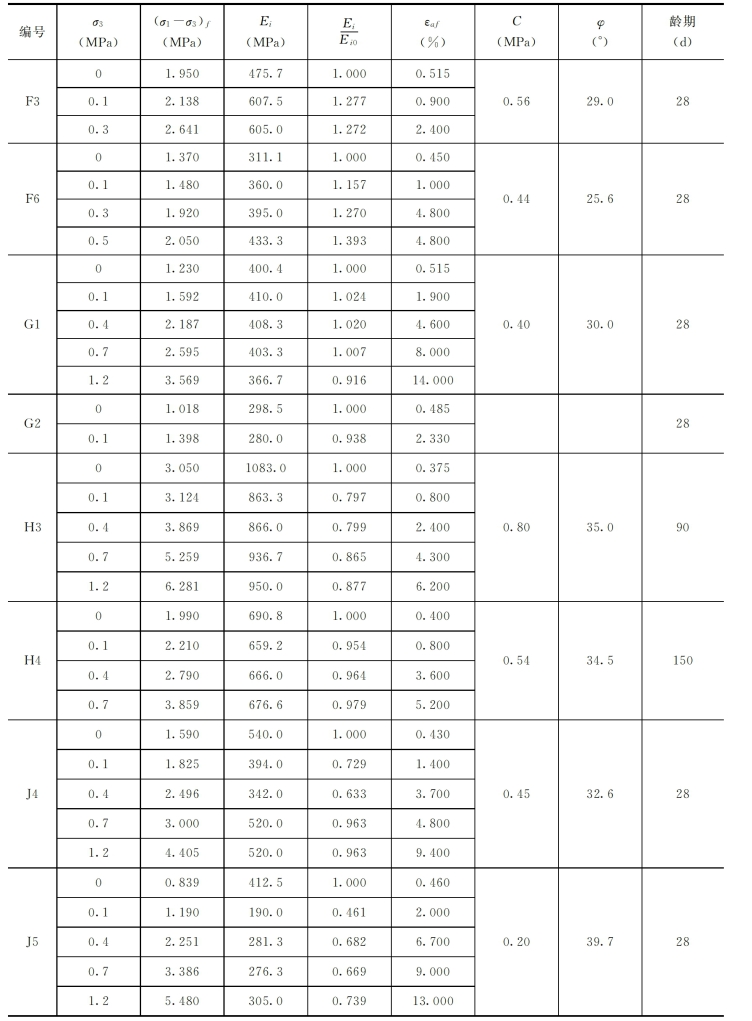
续表

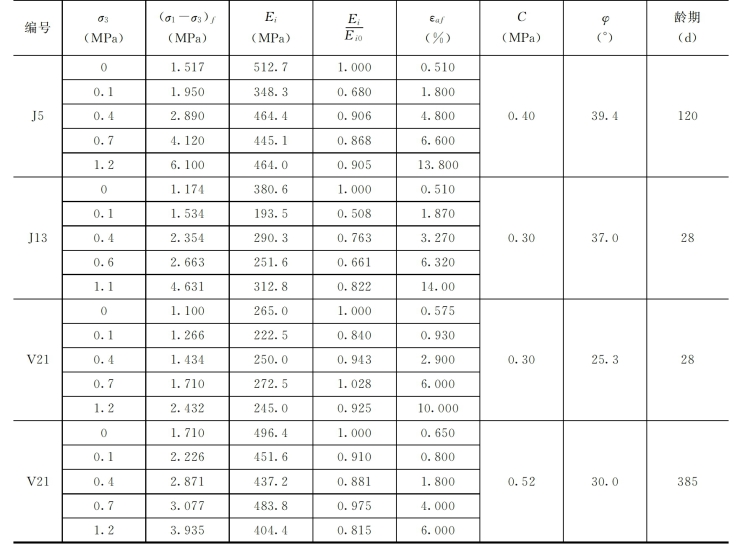
注　Ei0—单轴下的初始模量。

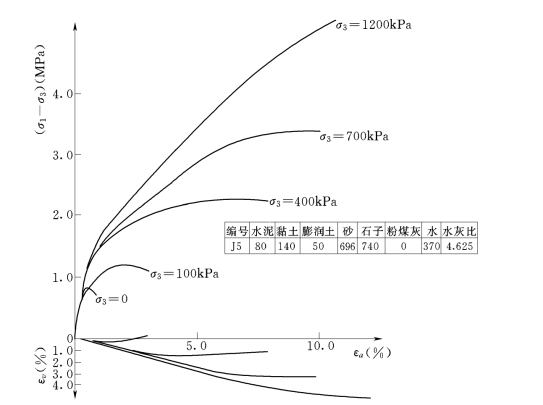
图3-7　J5试样28d（σ1-σ3）—εa—εv关系曲线图

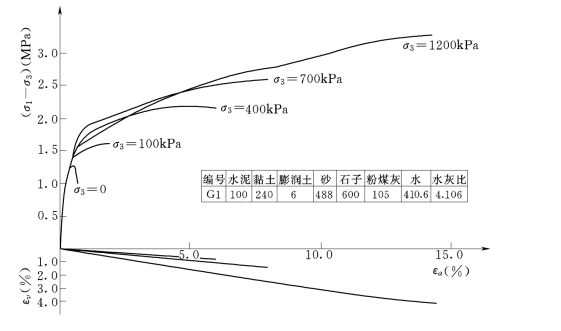
图3-8　G1试样28d（σ1—σ3）—εa—εv关系曲线图

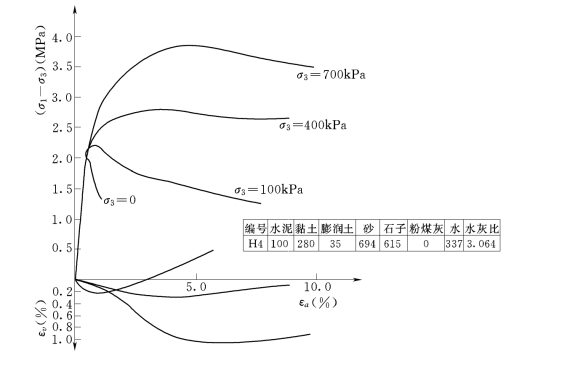
图3-9　H4试样150d（σ1-σ3）—εa—εv关系曲线图

由上述曲线可以看出［3］，塑性混凝土的应力应变关系曲线明显地存在一个类似比例极限的折点，其数值约相当于无侧限条件下试样脆性破坏的峰值强度，其峰值应变一般在0.4%～0.7%的范围内变化。在该折点以下，材料的应力应变关系近似于直线，其斜率为初始模量Ei。随着四围压力σ3的加大，应力应变关系逐渐变为加工硬化曲线，体变由剪胀逐渐变为剪缩，表现出明显的非线性性质，并接近于土料的性质。这表明它与土坝和覆盖层具有相似的本构关系。

此外，由表3-2和图3-7～图3-10还可以看出，随着四围压力的增大，塑性混凝土的强度和极限应变εaf有明显的增大。表3-4、表3-5和图3-11、图3-12分别给出了塑性混凝土强度σ1和峰值应变εaf与四围压力σ3的关系。

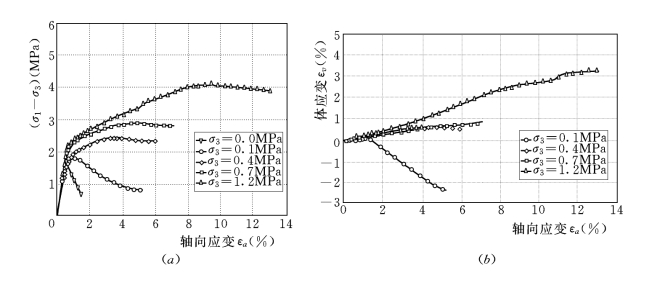
图3-10　J4试样28d（σ1-σ3）—εa及εv—εa关系曲线图

表3-4　四围压力σ3对塑性混凝土抗压强度的影响

续表

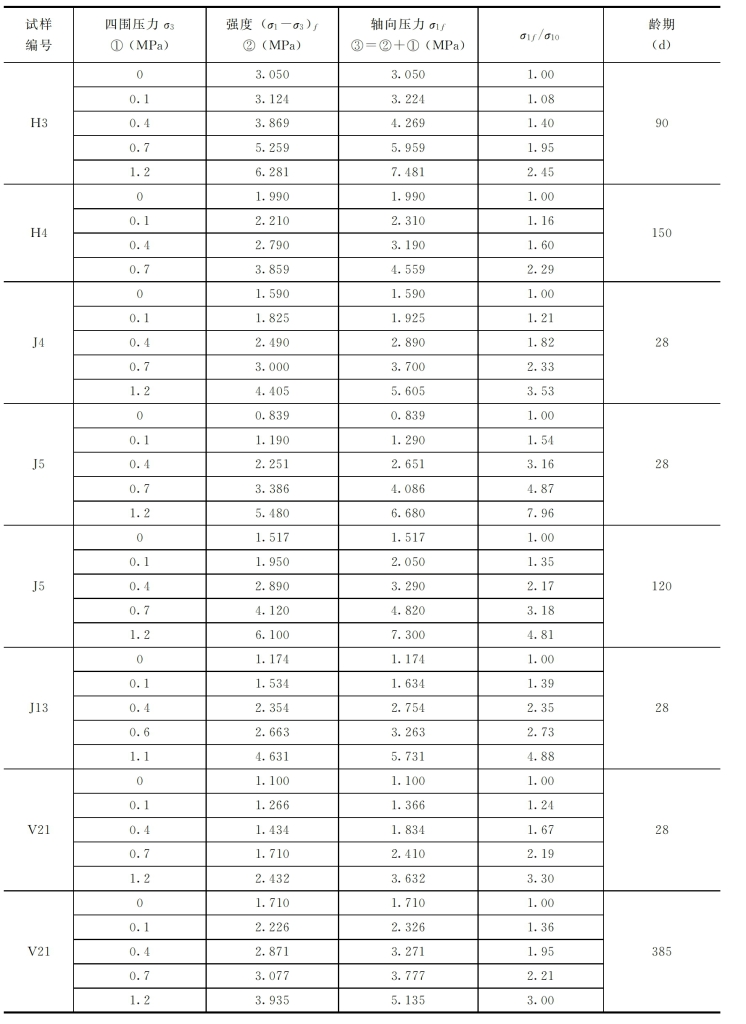
表3-5　四围压力σ3对塑性混凝土极限应变εaf的影响

(www.daowen.com)

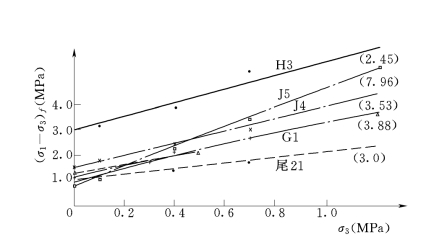
图3-11　（σ1-σ3）f与σ3的关系曲线图

注：括号内数字是σ3=1.2MPa时的σ1为无侧限时σ1的倍数

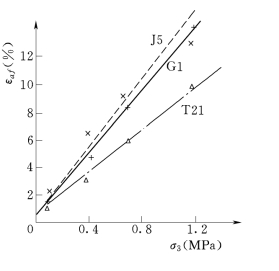
图3-12　三轴试验峰值应变与侧限压力关系图

由表3-3、表3-4及图3-11、图3-12可以看出，塑性混凝土的抗压强度σ1f和极限应变εaf几乎随着σ3增加而呈直线增大。当σ3由0增至0.5MPa时，抗压强度σ1f一般增大2倍左右；当σ3增至1.2MPa时，σ1f增大2～8倍。而极限应变εaf的增加更大，如当σ3增加至0.5MPa时，εaf增大13～19倍，达到4%～8%；当σ3增至1.2MPa时，εf增大16.5～28.3倍，达到6%～14%。而刚性混凝土的极限应变为0.08%～0.3%，仅为塑性混凝土数1/10。实际上，防渗墙总是工作在三向受力的条件下，这说明塑性混凝土以单轴抗压强度来判断其安全性是非常保守的，也是荒谬的，其实际的抗压安全系数要大几倍，至于抗裂安全系数就更大了。

3.四围压力对塑性混凝土初始模量的影响

土料的初始模量Ei随着四围压力σ3的增加而明显加大，Janbu（1963）［4］建议用一指数函数来描述两者之间的关系：

式中　K、n——试验常数，由一组常规三轴试验确定；Pa为大气压力。

塑性混凝土试样在不同的四围压力σ3时的初始模量Ei值见表3-3。由表3-3可以看出，塑性混凝土试样的初始模量Ei整体上不随四围压力的增加而加大（仅极少数式样略有增加），甚至反而有所减小。塑性混凝土的这一力学特性与地基土和回填击实黏性土完全不同。对此进行统计分析并用t检验法来检验无侧限和三轴条件下初始模量的差异性。显著性水平α=0.05。如表3-6所示，无侧限压缩试验初始模量Ei样本共n1=148个元素，三轴试验初始模量Ei样本n2=36个元素，归一化均值分别为X1=1.000，X2=0.940，三轴条件下的初始模量Ei比无侧限条件下的平均值要小，但无显著性差异。

表3-6　单轴、三轴弹模统计比较表

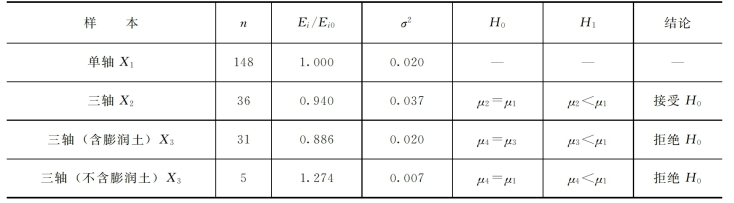
注　Ei0为单轴下的初始模量；Ei为三轴下的初始模量。

从表3-3还可以看出，与无侧限条件下相比，塑性混凝土的初始模量Ei在四围压力σ3作用下有所减、增，与其配比中是否掺有膨润土有关，塑性混凝土中凡掺有膨润土时，三轴条件下的初始模量的平均值比无侧限条件下的初始模量小；反之，则三轴条件下的初始模量的平均值较大，且无一例外。表3-6统计资料表明，两者均呈显著性差异。

表3-7　膨润土含量与初始模量

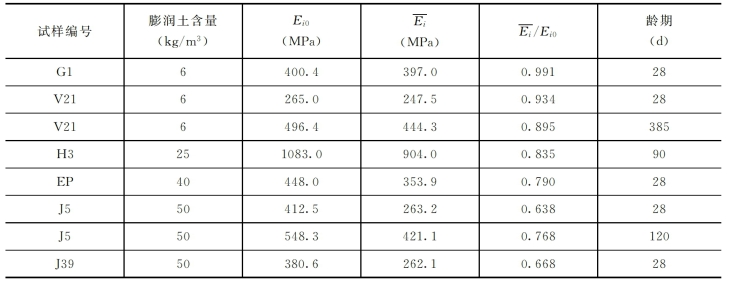
这种塑性混凝土的初始模量Ei不随四围压力σ3的加大而增加的特性，与一般土料的初始模量Ei随四围压力σ3增加而明显加大的性质是完全不同的。塑性混凝土的这一力学特性，对塑性混凝土在土石坝尤其是中高土石坝基础防渗墙中应用的合理性，提供了一个新的重要依据。当防渗墙周围的土体由于坝身填土的加高四围压力的加大其初始模量增加时，塑性混凝土防渗墙的初始模量却并不增大，这必将使作用在防渗墙上的荷载向周围土体转移，从而降低了墙体的应力；同时，由于四围压力σ3的作用，使塑性混凝土的强度与极限应变显著提高，这些均将改善塑性墙的工作条件，增加其安全性。

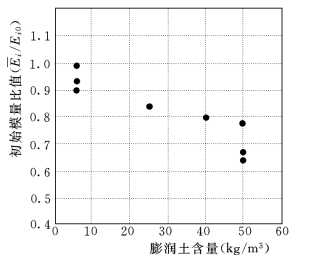
图3-13　三轴单轴初始模量比与膨润土含量的关系

与刚性混凝土相比，塑性混凝土具有很低的变形模量和较低的模强比，其模强比一般为50～500，而刚性混凝土的模强比可达1000～3000左右，这表明在同样的工作条件下，塑性混凝土墙的应力会小很多。

4.龄期对塑性混凝土力学特性的影响

通过不同龄期的无侧限压缩试验结果，研究了龄期对塑性混凝土的强度qu、初始模量Ei和峰值应变εaf的影响。试验结果指出，qu和Ei随龄期的增长而明显增加。由表3-8［1］、表3-9和图3-14可知，90d、180d和1a强度分别约为28d强度的1.6倍、2.0倍和2.7倍。28d以后，强度qut和初始模量Eit随龄期t增长的关系可近似用下式表示：

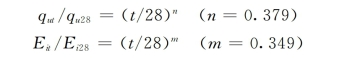
式中指数m与n十分接近，说明塑性混凝土的强度和初始模量基本上随龄期同步增长。

但峰值应变εaf基本不能随龄期变化，并不因初始模量的增加而减小，这一特性对于塑性混凝土的受力条件显然是有利的。

长江科学研究院进行了360d的试验［5］，得出了相近的结果，如表3-8所示。

表3-8　不同龄期无侧限试验成果表

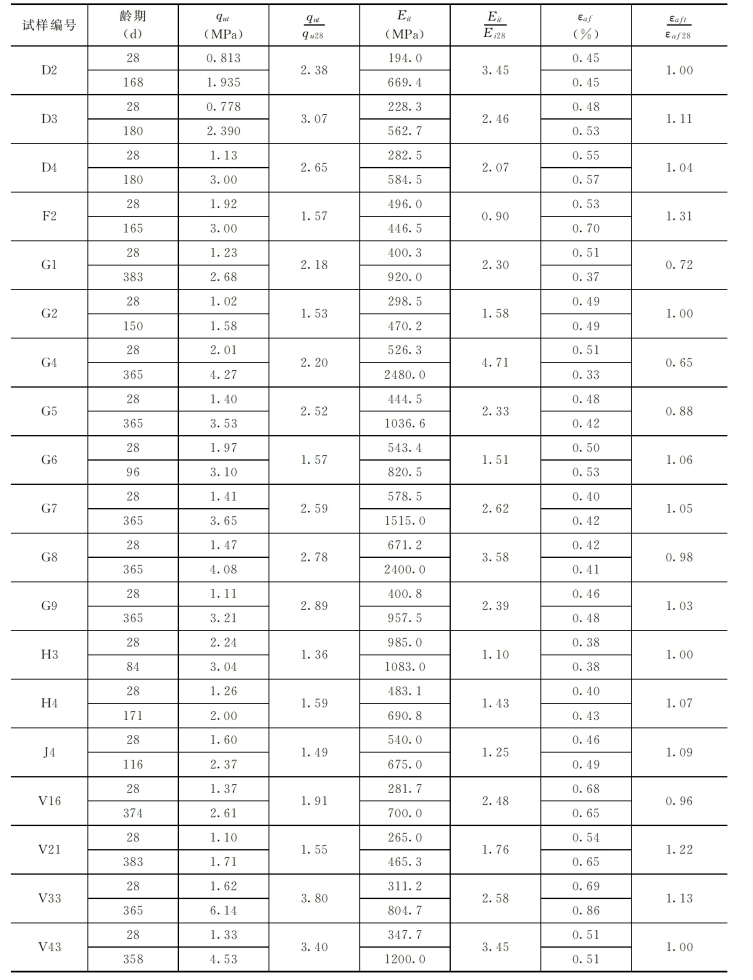
表3-9　塑性混凝土强度、模量、模强比与龄期的关系

注　表中括号内数字为与28d龄期的比值。

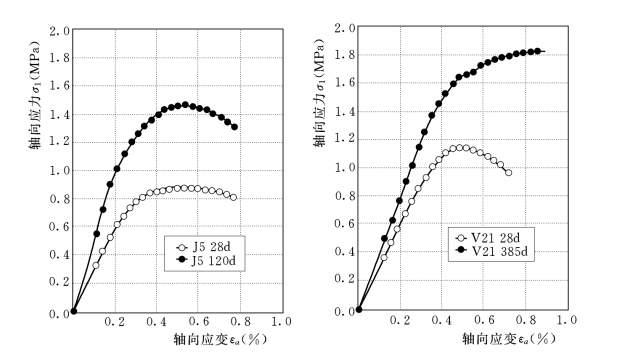
图3-14　不同龄期无侧限压缩应力应变曲线比较图

法国Costaz，J.Tardieu，B.［6］进行试验研究，他们所作的1000d龄期试验如图3-15所示。随着龄期的延长，其抗压强度大大提高，而且其提高的倍数与塑性混凝土的灰水比有密切关系，灰水比越大，这一倍数越小。

上述资料表明，塑性混凝土的无侧限抗压强度qu和初始模量Ei几乎同步增长，甚至延续数年。但模强比随龄期增长略有下降，这又一次表明塑性混凝土防渗墙的安全系数随龄期增长而增大。

5.加荷速率对塑性混凝土力学特性的影响

为了研究加荷速率对塑性混凝土力学特性的影响，对三个配比G2、G6和H4试样进行了不同加荷速率下的无侧限压缩试验，试验速率的变化范围为2～0.0004mm/min，同时对H4试样在四围压力σ3=0.1MPa时分别采用速率为0.02mm/min和0.0004mm/min进行三轴试验。当速率为0.0004mm/min时，每一试验需进行25昼夜。上述试验得到的强度、初始模量、峰值应变及对速率为0.2mm/min相应指标的归一化成果如表3-10所示，对强度的归一化曲线如图3-16所示。速率不同时三周试验成果见表3-11。

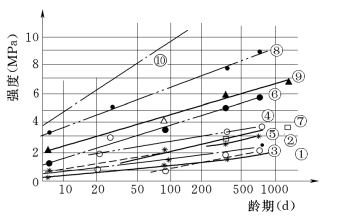
图3-15　塑性混凝土抗压强度随时间增长曲线图

①—水灰比0.25；②—水灰比0.33；③—水灰比0.36；④—水灰比0.39；⑤—水灰比0.4；⑥—水灰比0.44；⑦—水灰比0.46；⑧—水灰比0.55；⑨—水灰比0.71；⑩—水灰比1.05

表3-10　无侧限不同速率试验成果表

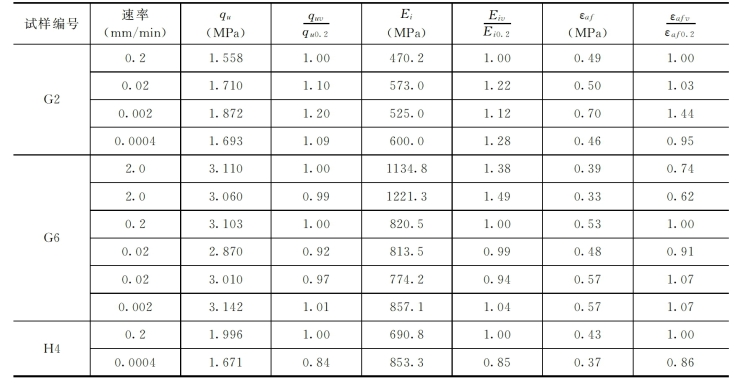
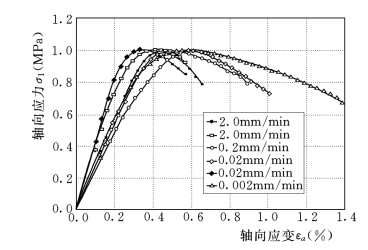
图3-16　G6试样不同加载速率下归一化应力应变曲线图

由以上成果可以看出，速率的影响有以下几点：

（1）速率等于0.2mm/min时，塑性混凝土试样无侧限压缩试验的初始模量Ei有明显增加，而峰值应变εaf则有显著的减少。

（2）速率小于0.2mm/min时，无侧限压缩试验各项力学特性指标与速率为0.2mm/min的相比，无显著差异，这表明无侧限试验采用0.2mm/min的速率是合适的。

（3）由图3-16，通过对不同速率下以强度归一化的应力应变曲线σ1/qu—εa线型的比较，可以看出速率小于0.2mm/min时，峰值前归一化的应力应变曲线基本相同，峰值后各曲线随速率的变化无明显的规律性，其原因可能与峰值后为不稳定状态有关。

（4）加荷速率分别为0.02mm/min、0.0004mm/min的三轴试验结果比较表明，试样的峰值强度、初始模量和峰值应变均无明显差别，如表3-11所示。

表3-11　三轴试验不同速率成果比较表

表3-12　塑性混凝土无侧限抗压强度受试样形状的影响

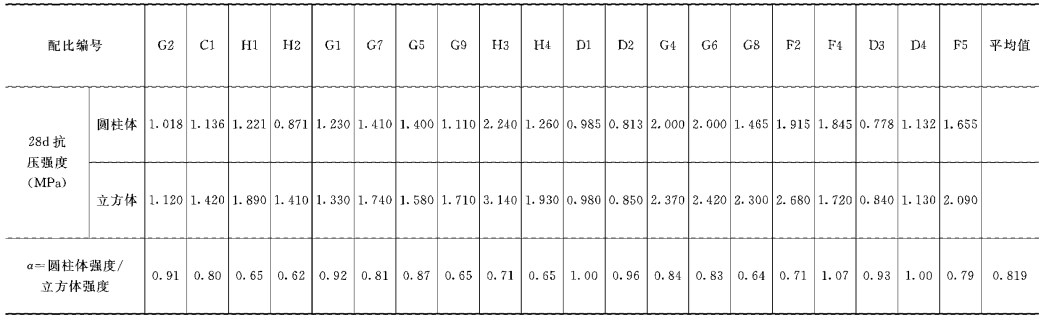
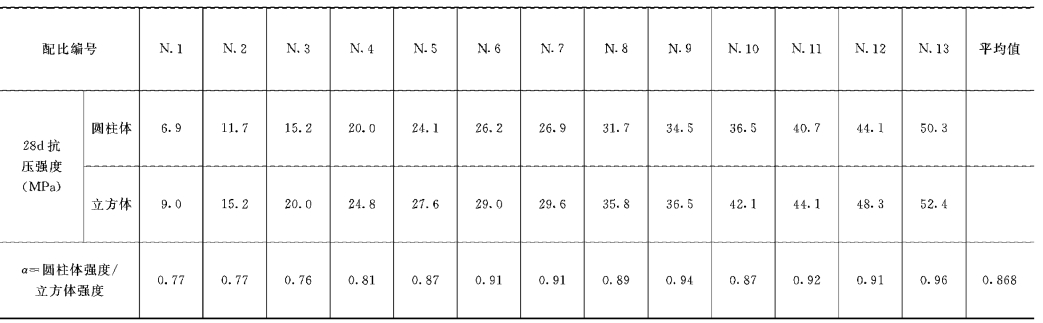
表3-13　刚性混凝土抗压强度受试样形状的影响

6.试样形状对塑性混凝土无侧限强度的影响

为了研究试样形状的影响，分别对20组配合比的20cm×20cm的正方体试样和直径为15cm、高20cm的圆柱体试样进行了28d龄期无侧限压缩试验，试验结果示于表3-12和图3-17中。为了作对比分析，同时在表3-13中列出试样形状对刚性混凝土强度的影响［7］。

由上述图表可以看出，试样形状不同，但其抗压强度较为接近。用α表示圆柱体试样强度与立方体试样强度的比值。

此外，根据文献［7］第553页所给出的如图3-18所示的研究结果，当采用圆柱体试样时，其高径比（h/d）为2是合适的。文献［7］同时指出，采用h/d=2的高径比，不仅因为可以大大消除试样端部的影响，使其中部的受力状态为轴心受压，还因为此时即便发生少许偏差，也不致严重影响强度的测定值。