对于特别重要的、规模大和永久性工程，比如三峡二期围堰防渗墙的配合比设计，由于该防渗墙的作用水头大，墙体应力大，要求安全度高；同时，由于该工程规模大，工程费用高，力求节省投资。因此在该工程的配合比设计中，投入了大量的物力、人力和时间，配合比设计工作受到高度的重视，采用优化配比设计方法。

三峡围堰在不同部位分别采用塑性混凝土和柔性混凝土。对这两种混凝土分别采用了两种设计方法：正交设计法和均匀设计法。现分述如下：

（一）正交设计法

用于塑性混凝土配合比设计。这项配比设计工作是由长江水利委员会长江科学院和清华大学合作进行的。具体设计工作如下。

1.配合比设计要求的技术指标

配合比设计要求的技术指标如下：

（1）抗压强度：R28≥2.0MPa。

（2）模强比：Ei/R28≤250。

（3）渗透系数：K≤10-7cm/s。

（4）塌落度：SP≥18～22cm。

2.配合比的设计方法和步骤

根据上述确定的指标，并考虑到三峡工程的重要性，对配合比设计和试验工作采取了三阶段逐步淘汰的优选法。设计工作是遵循了蔡正泳著的《正交设计在混凝土中的应用》［4］一书中的理论进行。以下分别按三步说明配比设计和试验工作情况［5］。

（1）配合比设计。为了选出既能满足三峡二期围堰塑性混凝土防渗墙设计指标要求，并考虑三峡工程的重要性，必须从众多的方案中选出最优的配比，但又能减少工作量，为此我们采用配合比的正交设计方法。为了使所选方案具有广泛性，我们在设计中采用6因素（水泥、膨润土、黏土、砂、碎石和水）和5水平（见表2-13）进行配比设计。按通常情况任意组合，就会组成56=15625个配合比，要完成这么多试验工作是很难的。而正交设计理论利用“均衡分散性”与“整齐可比性”的正交性原理制成如文献［4］第213页所列的正交表，将15625个配合比变成25个配合比（见表2-14）大大简化了试验工作。

表2-13　配合比设计中6因素5水平表

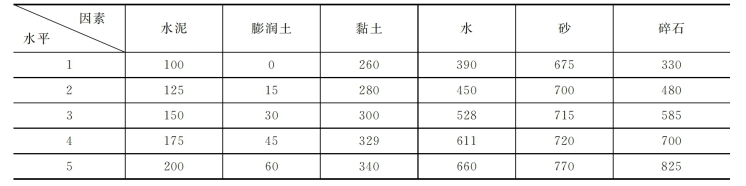
表2-14　L25（56）正交表（选自文献［4］第213页）

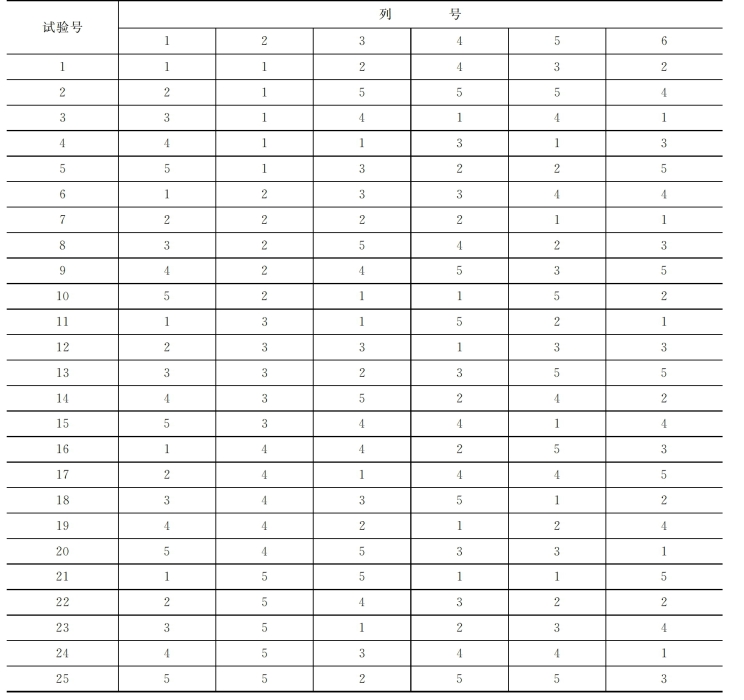
经过上述设计，得到了初选的塑性混凝土配合比表，如表2-15所示。

表2-15　塑性混凝土配合比表

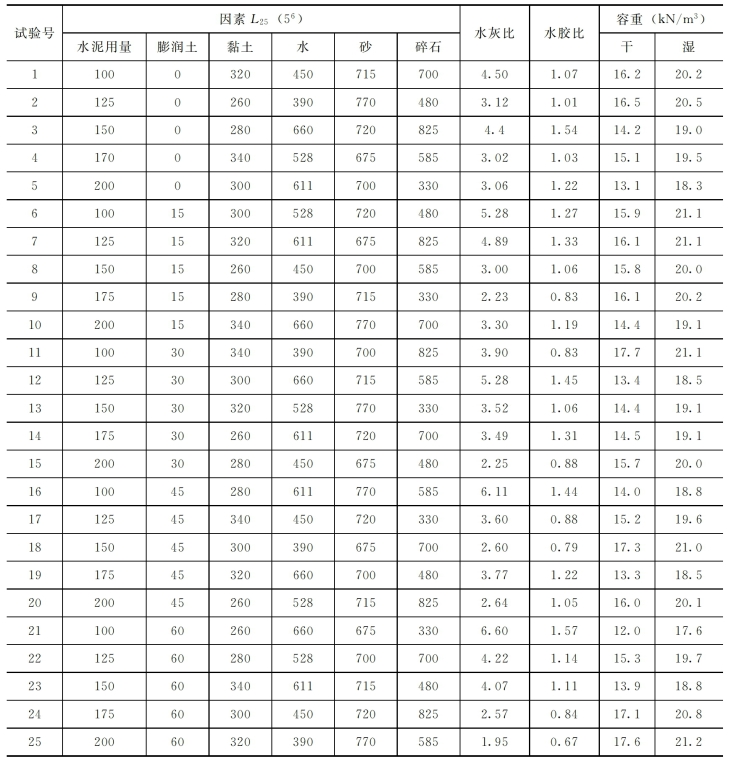
（2）配合比试验。为了实施逐步淘汰方法，我们采用了初选、复选和终选三阶段试验步骤。力学试验是用直径15cm、高30cm的试件在英国制造的WF—10072高压三轴仪上以0.2mm/min加载速率进行的。渗透试验是用φ150mm、高120mm试件在于玉贞研制［1］的渗透仪上进行的。

1）初选试验。由于经费所限，在初选试验中未按原计划作25个配比，只作了20个配比，将2号、8号、12号、16号和23号配比取消了。

按计划这一阶段只作无侧限压缩试验，测定抗压强度和初始模量。

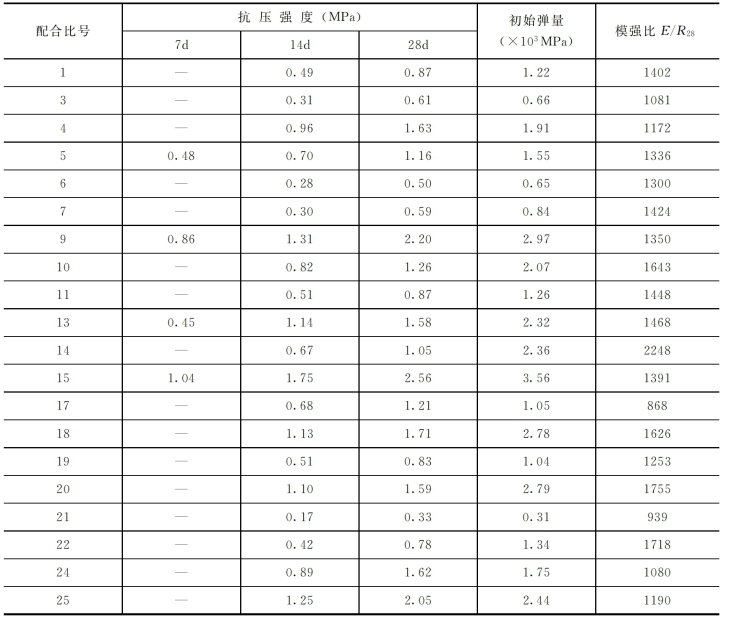
初选试验结果如表2-16所示。由表2-16可知在25个配比中有3个配比（9号、15号和25号）28d抗压强度超过2MPa，达到强度指标要求。但测量初始模量工作存在问题，使所测得的初始模量太高，模强比太大，故此未能达到预期要求。使得在初选阶段原本应同时考虑抗压强度和模强比两项指标进行优选，此时只能根据抗压强度进行优选。

表2-16　初选试验结果表

2）复选试验。复选试验配比的确定如下：

如上所述由于初选试验的初始模量存在问题，因此复选试验的配合比只是根据强度来确定。据此我们选出4号、13号、15号、20号和24号5个配合比进行复选试验。选定这5个配比属两种类型：一种是强度较高的，如15号，其圆柱抗压强度R28=2.56MPa；另一种一方面要使强度高，同时要便于施工，选用强度和水灰比都较高的，其余4个配比即属此类。

在进行复选试验时，考虑到长江水利委员会设计院要求R28≥4MPa，为此我们参照高掺粉煤灰的原则，在原配合比中加入与水泥用量相等的粉煤灰，以提高塑性混凝土的强度，复选试验的配合比如表2-17所示。为与原配比区别，在原配比号右上角加上“'”表示复选试验的配合比编号。

表2-17　复选试验配合比

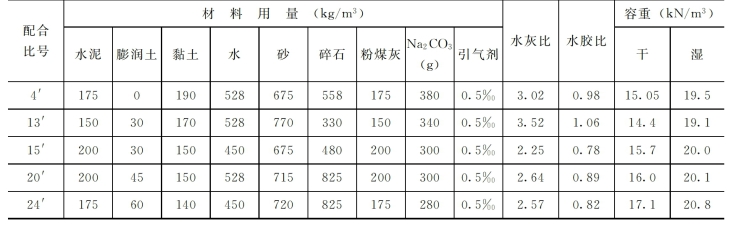
复选进行了单轴压缩和渗透试验，试验结果如表2-18所示。

上述试验结果表明：①增加粉煤灰对提高强度的效果很好，可提高强度0.8～1.82倍；②所选配合比的强度基本上达到设计要求，R28接近或超过4MPa。模强比也基本达到了设计要求。

表2-18　复选配合比强度试验成果表

注　1.24'号配比因北京降温，试件养护温度低，故强度偏低。
2.试件在上述水力比降作用100h以上，未见渗流增大，更未见颗粒析出。

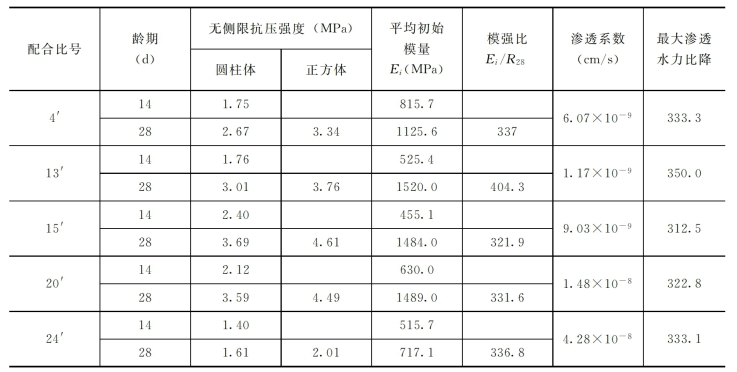
3）终选试验。最后我们根据表2-18所示的复选试验结果，选出两个配合比15号和20号进行终选试验，因为该配合比的强度、模强比和渗透系数均满足设计要求。终选试验项目为三轴压缩试验，三轴试验结果见表2-19和表2-20。

3.用优选配比参数对围堰防渗墙进行应力应变复核计算

（1）计算目的。

1）复核用所选配合比材料参数进行应力应变计算以确定三峡二期围堰防渗墙的结构安全性。

表2-19　三轴压缩试验测定的强度（28d）

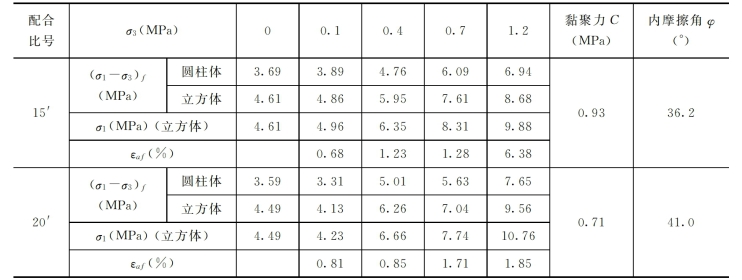
表2-20　三轴压缩试验测定的邓肯参数

2）通过计算最后选定三峡二期围堰防渗墙材料的配合比。

（2）计算程序、计算方法与计算参数。

1）计算程序：采用清华大学水利水电工程系编写的有限元计算程序GPDFA。该程序采用邓肯·张非线性模型，并考虑了防渗墙表面GOODMAN模型。

2）计算采用的网格、加荷程序、围堰计算断面和计算条件均按1995年4月召开的《三峡二期围堰有限元计算》会议确定的条件进行，在此不予详述。

3）计算参数如表2-21所示。

（3）计算结果。本次同时采用E—B模型和E—μ模型进行了计算。计算结果汇总于表2-22。

（4）结果分析。由表2-22可以看出以下几点：

2）墙体位移。用两种配比材料建造的防渗墙的最大位移非常接近，上游墙的水平位移为41.6～41.9cm，下游墙的水平位移为12.8～13.0cm；上游墙的垂直位移为18.2～20.7cm，下游墙的垂直位移为13.7～15.0cm。

表2-21　应力应变计算采用的参数

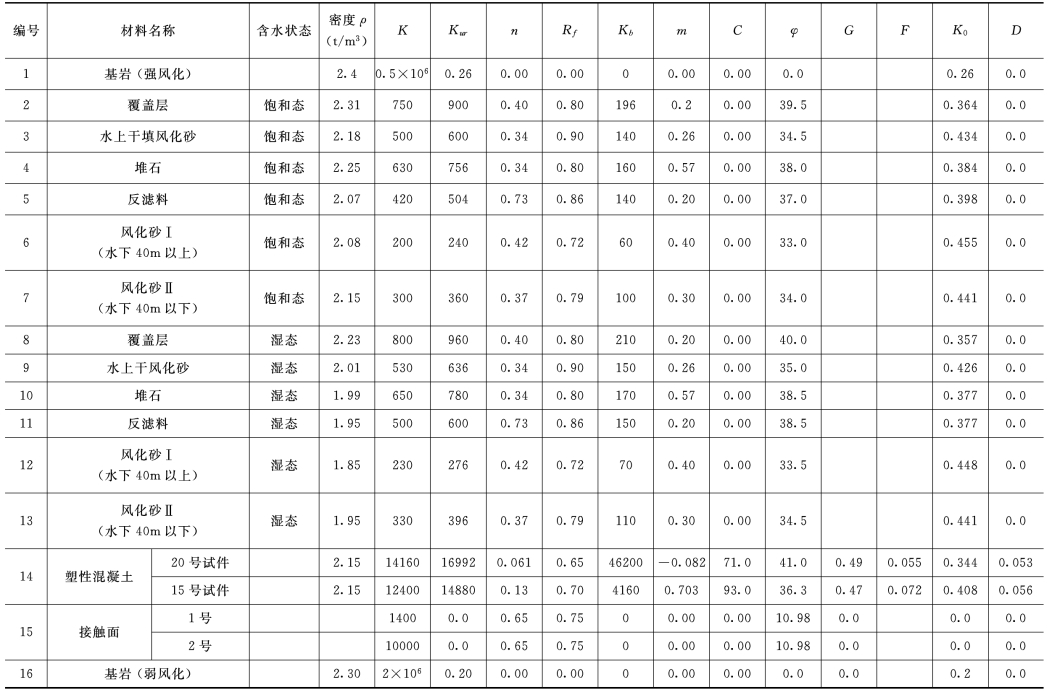
表2-22　各方案墙体应力最大值汇总表

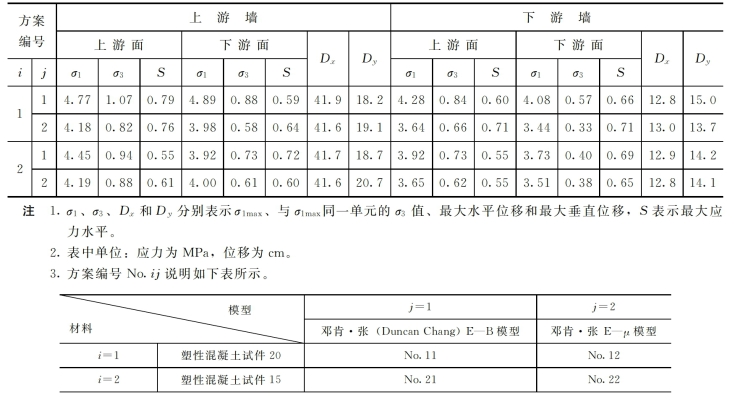
3）应力水平。上游墙的应力水平：除基岩附近单元应力水平高外，大部分单元应力水平小于0.6。其中上游墙：20'号配比S=0.59～0.79，15'号配比S=0.55～0.72。下游墙：20'号配比S=0.60～0.71，15'号配比S=0.55～0.71。整体来说：相应20'号试件的应力水平高于15'号试件的；上游墙的应力水平高于下游墙的应力水平。

4）两种模型E—B、E—μ模型计算的结果基本相近，只有较小的差别。其中E—μ模型计算的应力比E—B模型小0.6MPa左右；应力水平小0.05～0.1左右；但E—μ模型计算的变形比E—B模型大1～2cm。

4.最终结论——推荐采用15'配比为三峡二期围堰塑性混凝土配合比

通过上述应力变位计算和试验研究可得出如下结论：

（1）通过配合比设计三阶段的优选试验和应力变位计算可以认为：所选的15'号和20'号配合比从结构安全、防渗和施工三方面看都能满足三峡工程二期围堰设计的要求，但15'号配合比更好些，故此，我们推荐15'号配比为三峡二期围堰塑性混凝土防渗墙配合比。

（2）考虑到三峡工程二期围堰的重要性，也为通过三峡工程二期围堰塑性混凝土配合比研究使塑性混凝土配合比研究工作取得经验，我们遵循了一套严格的科研技术路线：用应力应变计算确定该工程塑性混凝土技术指标→正交配比设计确定配合比→三阶段淘汰法优选配合比→应力应变计算确定推荐配合比。最后选出了以水泥、黏土、膨润土和粉煤灰为胶结料的高强度低模强比的塑性混凝土配合比。

（3）通过试验研究摸索出塑性混凝土配合比设计的规律性，如影响塑性混凝土强度的因素的贡献大小以及各种因素的最优用量，这为今后塑性配合比设计提出了重要的经验。

（4）通过两次19个方案的应力应变计算，为三峡工程二期围堰最后选定塑性混凝土防渗墙和采用双墙方案及其参数提供了重要依据。(www.daowen.com)

（5）复选试验测定的渗透系数小于10-8cm/s，最大水力梯大于310，抗渗透破坏安全系数大于9.3，故防渗效果是良好的。

（二）均匀设计法

均匀设计法主要用于进行柔性混凝土防渗墙的配合比设计。

三峡二期围堰同时使用了塑性混凝土防渗墙和柔性混凝土防渗墙，后者是不含任何粗骨料，仅用当地风化砂、黏土和水泥等组成的防渗材料。长江水利委员会长江科学院对这种防渗材料进行了大量的试验研究，最终成功地应用于三峡二期围堰之中，获得了良好的防渗效果。

长江水利委员会长江科学院利用均匀设计法，成功地设计了柔性混凝土防渗材料的配合比［6］。

由于三峡二期围堰所要求的力学指标很高，其28d强度达到4～5MPa，而模强比小于250，渗透系数小于10-7cm/s。因此，各组成材料的含量需要设定较宽的变化范围进行考虑。将上述三因素（即各主要原材料）划分为10个含量等级（在试验中称为水平）来对比研究，从而形成了3因素10水平的试验方案，如表2-23所示。

表2-23　柔性材料原材料含量等级（因素）划分

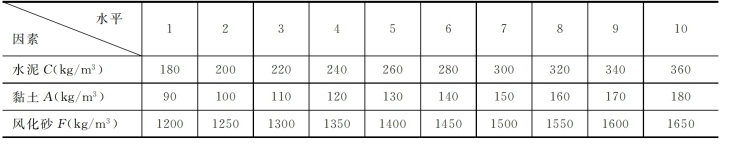
该3因素10水平的全面试验组合，共有1000组，这么大的试验组数是难以进行的，为此需要进行专门的试验设计来挑选有代表性的试验点。这种试验设计的方法有多种，不同的方法有不同的精度和工作量，例如最常用的是正交设计方法，其特点是“均匀分散，整齐可比”。但3因素10水平试验若用正交设计理论，仍需进行至少100组配比试验，工作量仍然很大，因此必须寻求新的配合比设计方法，为此采用了均匀设计方法。

1.应用均匀设计方法进行配合比设计

均匀设计方法是方开泰于1994年在《均匀设计与均匀设计表》［7］一书中提出的一种崭新的试验设计方法，此法非常适合于多水平的试验设计。现将均匀设计方法简单介绍如下：

“均匀设计是只考虑试验点在试验范围内均匀散布的一种试验方法”，它的数学原理是数论中的一致分布理论。均匀设计挑选试验点的出发点是“均匀分布”，而不是考虑“整齐可比”，因而与正交设计相比可大幅度降低试验工作量。例如，当试验中有s个因素，每个因素有q个水平时，则所有可能的试验共有qs种组合，如本例就有103=1000种组合，正交设计方法从中挑选出q2=102=100个点，而均匀设计法是利用数论中的一致分布理论只选取q个点进行试验，其效果与全面试验相近，这就大大减少了试验工作量，节省了大量的人力、物力和财力。还由于应用数论方法使试验点在积分范围内散布得十分均匀，因此便于计算机统计建模。

对于上述柔性材料的配合比试验，s=3，q=10，可利用文献［7］中第71页A1.8给出的均匀设计表U10（108），从U10（108）的使用表可查得s=3时，使用U10（108）的第1列、第5列、第6列来安排试验均匀性最好，均匀设计的试验方案如表2-24所示。由表2-24可知，三峡二期围堰柔性材料只做10个配比试验即可。

表2-24　柔性材料配合比试验的均匀设计表

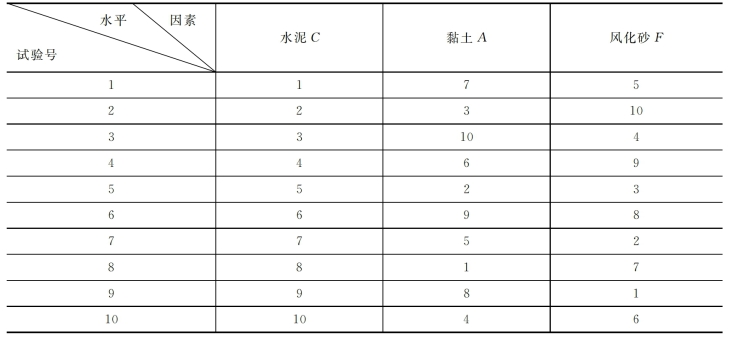
表2-24中试验号即配合比编号，共10组配合比，其对应的行表示各因素的不同水平组合。例如，1号配合比表示水泥取第1水平，黏土取第7水平，风化砂取第5水平，由表2-23的各因素水平等级划分中可查得该组配合比为：水泥180kg/m3，黏土150kg/m3，风化砂1400kg/m3。

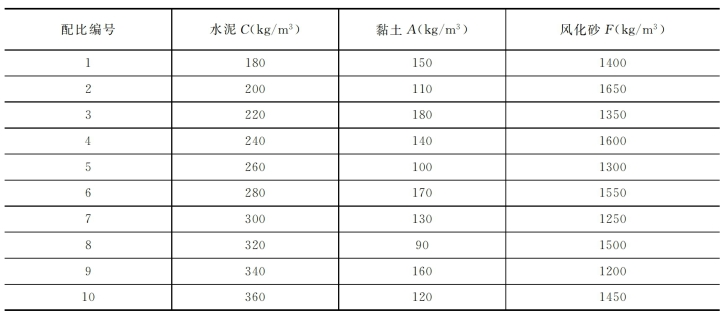
将表2-23中各个材料的水平值填入表2-24，即可得到10个柔性混凝土的配合比，如表2-25所示。

表2-25　柔性混凝土配合比表

2.配合比试验

配合比试验的试件尺寸、试验方法和试验设备与正交设计方法相同。

（1）初选试验。初选试验只进行单轴压缩试验，试验结果见表2-26。

表2-26　柔性材料配合比试验成果表

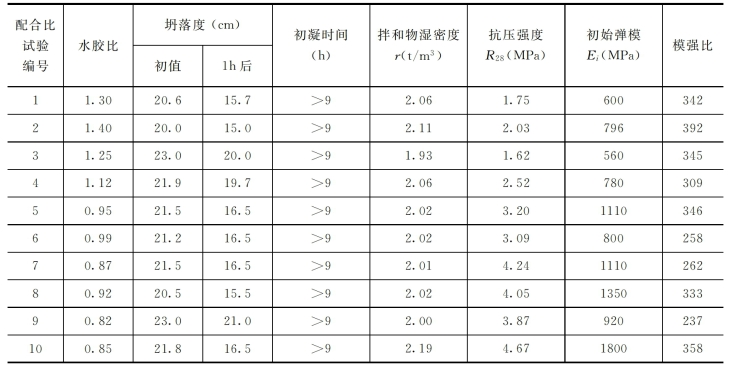
由表2-26可以看出，6号、7号和9号配合比的强度分别为3.09MPa、4.24MPa和3.87MPa，模强比分别为258、262和237。均与设计要求的强度大于4MPa、模强比小于250的要求相接近，因此，初步选定上述3个配合比作为进一步比较的配合比。

但是，所选的3组配合比的力学指标与设计要求存在一定的差距，为此需要进一步在更为广泛的范围进行优化设计，这里，我们特别提出采用近年来得以广泛应用的人工神经网络技术（ANN）进行优化设计。

（2）优化配合比设计。将人工神经网络技术应用在三峡二期围堰柔性材料配合比设计中，建立柔性材料的配合比图谱。

人工神经网络建模过程就是根据系统的输入、输出样本，对网络进行训练，使人工神经网络模型逼近实际系统的输入、输出关系。

人工神经网络的训练方法和计算模型有多种，三峡二期围堰柔性材料配合比设计的计算模型采用较为成熟且应用最广的误差反传播法（简称BP模型）。采用三层网络，结构为3×10×2。三个输入端点分别代表柔性材料原材料中的水泥、黏土和风化砂的含量（kg/m3），两个输出端点分别代表该组配合比柔性材料的抗压强度（R28）和初始切线模量（Ei）。作者用Turbo C语言编写并已成功应用过人工神经网络模拟软件ANN—BP1。

根据建立的ANN模型，可以预测出数百组满足如下条件的柔性材料配合比，即：强度R28＞3MPa，模强比为250左右。为了直观起见，将模型的预测数据降维处理，即先将柔性材料三种原材料中水泥含量（kg/m3）固定，由ANN模型计算出在该水泥含量下黏土含量与风化砂含量的不同组合形成的柔性材料的强度和相应的模强比，如此形成水泥含量（kg/m3）分别为250、260、270、280、290和300的图谱，据此可达到优化配合比的目的。图2-6是水泥用量分别为280kg/m3、290kg/m3和300kg/m3时的配合比图谱。

在图2-6所示的图谱中，纵横坐标分别表示柔性材料配合比中的黏土和风化砂的含量，它们与表头水泥含量组合，则对应一组配合比，因而图中每一点均对应一组配合比。而图中标出的阴影区域表示那些满足不同力学指标要求的配合比（点）的集合。因此，根据不同的力学指标要求，可以很方便地从图谱中查到所需的柔性材料配合比。

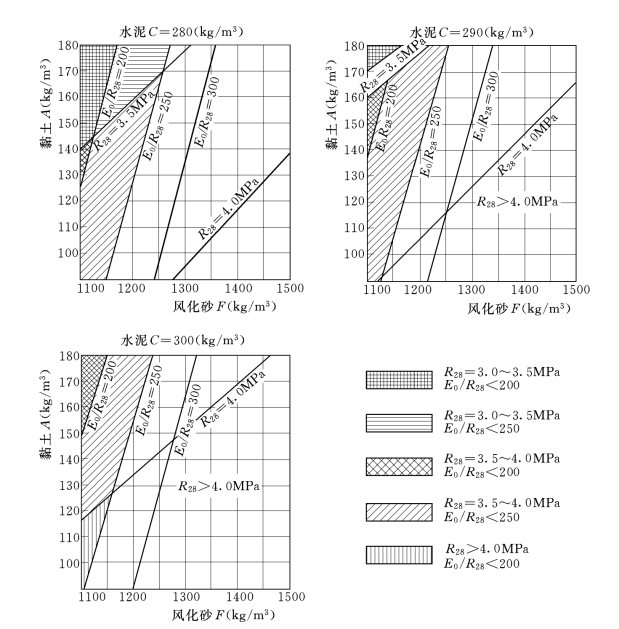
图2-6　柔性材料配合比图谱（水泥用量为280kg/m3、290kg/m3和300kg/m3）

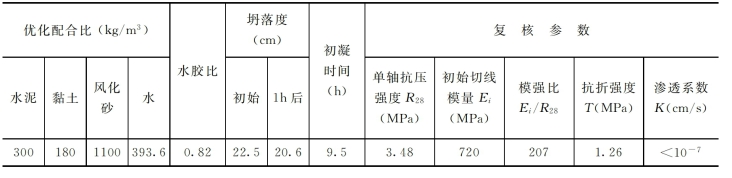
为寻求满足强度要求且模强比更低的优化配合比，在C=300kg/m3图谱中R28大于3.5MPa且模强比小于200的区域中选择出如下的配合比并进行了参数复核试验。该组配合比在图谱上查得的参数为：R28为3.62MPa，模强比为184，复核试验结果如表2-27所示。

表2-27　柔性材料优化配合比及其参数复核

实际上，柔性材料的配合比与力学参数的关系不是一个简单关系。由于试验误差和参数计算误差等因素，所建立的模型只能作为一个半定量模型，但这个半定量模型说明了以下两个规律：

1）满足某一给定力学指标要求的配合比在图谱中构成一个区域，这意味着在选定柔性材料配合比的情况下，柔性材料各组成（主要是黏土和风化砂）尚可在一个较宽松的范围内变动。

2）当要求柔性材料指标有变动的情况下（例如不同的工程所要求的指标不同），用所建立的半定量模型和配合比图谱可指导配合比的进一步优化，提高配合比设计质量。

（3）优化配合比试验。在“八五”攻关的后期，针对三峡二期围堰防渗墙体指标的要求，柔性材料的攻关指标提高为R28=4.0～5.0MPa，模强比小于250，因此又进行了相应优化配合比试验。

由图2-6所示的柔性材料配合比图谱中可以看出，满足抗压强度R28＞4.0MPa和模强比小于250的配合比范围很窄。这表明，在柔性材料原材料品种不变的情况下，仅仅依靠配合比的调整来满足上述指标要求，可供选择的余地较小。为此，将水泥品种做了调整，用425号矿渣水泥代替普硅水泥进行试验，以优选出满足工程要求的配合比。

在这次优化试验中，除了改用葛洲坝水泥厂生产的“三峡牌”425号矿渣硅酸盐水泥外，风化砂、黏土及外加剂不变。经过对比试验，由表2-28可以看出，在水泥用量由300kg/m3减少至280kg/m3，黏土减少的配合比下，用425号矿渣水泥代替425普硅水泥所形成的柔性材料强度有较大增长，由3.48MPa增至5.82MPa（或4.52MPa），相应的模强比基本不变，故此配合比得到优化。

表2-28　专题研究中优选出的柔性材料配合比及参数复核结果

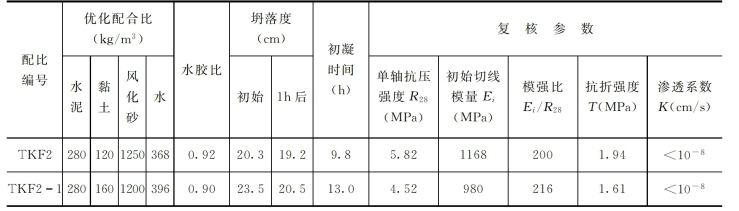
表2-28表明该2组配合比柔性材料的各项指标满足设计要求，但TKF2更优，最后选定此配比作为最终配合比。

（4）终选试验。对TKF2这组配合比的柔性材料，清华大学水利水电工程系进行了三轴剪切试验。三轴剪切试验分别采用围压0.1MPa、0.4MPa和0.7MPa进行固结排水试验，试验结果见表2-29。

根据三轴试验结果及其相应参数计算，求得邓肯·张非线性弹性E—μ、E—B模型参数值汇总于表2-30中。

表2-29　柔性材料（TKF2）三轴试验成果表

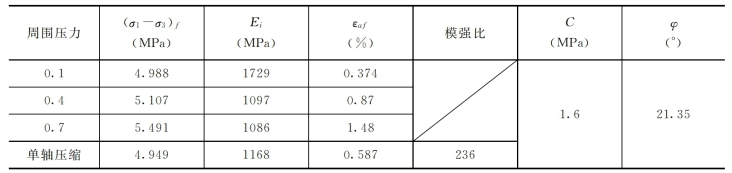
表2-30　柔性材料邓肯·张E—μ、E—B模型参数

3.防渗墙安全复核

清华大学对柔性材料（TKF2）用于二期围堰防渗墙（以三峡二期围堰为例）的安全性进行的邓肯·张E—B模型（j=1）和E—μ模型（j=2）的计算复核，结果见表2-31。

表2-31　三峡二期围堰柔性材料（TKF2）防渗墙墙体σ1、σ3、Dx、Dy、S汇总表

注　1.表中σ1、σ3、Dx和Dy分别表示σ1max、σ3max、最大水平位移和最大垂直位移，S表示应力水平。
2.表中单位：应力为MPa，位移为cm。

计算结果表明，墙体压应力均小于5.82MPa，无拉应力，且墙体最大应力水平为：在应力集中区为0.7左右，在非应力集中区为0.6左右，相应安全系数分别为1.7左右。所以，按莫尔—库伦强度准则和应力强度准则判断，用柔性材料构筑三峡二期围堰防渗墙是安全的。

综上所述，前面优选的柔性材料各项指标已达到攻关目标。据三峡二期围堰防渗墙最终确定的设计力学指标，正式推荐所优选的配合比TFK2被中国三峡开发总公司确定为三峡二期围堰柔性防渗墙材料的首选配合比。

根据设计研究，两种材料采用的部位分别是：塑性混凝土用于河床深槽部位（大约相当于墙高超过40m部分），其余部位采用风化砂柔性材料。

（三）两种配合比设计方法——正交设计法和均匀设计法比较

在三峡二期围堰防渗材料配合比设计中，同时使用了正交设计法和均匀设计法，应该认为这两种方法都是成功的，但同时又是有区别的，各有所长，可以相互补充；而且应用条件也有所不同，对于某个具体工程，应用哪种方法更好，要具体分析。为便于设计者应用，下面进行两方面的比较。

首先，正交设计方法具有正交性，如果试验按它设计，可以估计出因素的主效应，有时也能估出它们的交互效应。均匀设计方法是非正交设计，它不可能估计出方差分析模型中的主效应和交互效应，但是它可以估出回归模型中因素的主效应和交互效应。

其次，正交设计方法多应用于水平数不高的试验，因为它的试验数至少为水平数的平方。比如一项试验有5个因素，每个因素取31个水平，其全部组合有315=28625151个。若用正交设计，至少需要做312=961次试验，而用均匀设计，只需要做31次试验。所以，均匀设计适合于多因素多水平试验，如塑性混凝土6因素5水平的正交试验次数为25次，柔性材料3因素10水平的均匀试验次数只为10次。

再者，均匀设计方法提供的均匀设计表在选用时有较多的灵活性。例如，一项试验若每个因素取4个水平，用L16（45）来安排，只需做16次试验。若改为5水平，则需用L25（56）来安排，要做25次试验。从16次到25次对工业试验来讲，工作量有着显著的不同。又如在一项试验中，原计划用均匀设计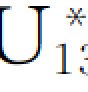（135）来安排5个因素，每个有13个水平。后来由于某种需要，每个因素改为14个水平，这时可用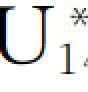（145）来安排，试验次数只需增加1次。均匀设计的这个性质，有人称为“试验次数随水平增加有连续性”，并称正交设计“有跳跃性”。

正交设计的数据分析程式简单，有一个计算器就可以了，且“直观分析”可以给出试验目标指标Y随每个因素的水平变化的规律。均匀设计的数据要用回归分析来处理，有时需用逐步回归等筛选变量的技巧，非使用计算机不可。幸好计算机在我国的普及程度已经相当高，因此均匀设计方法应用于配合比设计还是非常方便的。