前面介绍的都是线性问题，当遇到非线性的问题（例如异或问题）时，就需要用到核技巧将线性支持向量机推广到非线性支持向量机。具体地，通过引入非线性函数Φ（·）将训练样本映射到高维特征空间，在该高维空间中构造最优分类超平面，即将非线性问题转化为高维特征空间的线性分类问题来解决。这样在原始空间中线性不可分的训练样本在被映射到足够高维的空间中后变成线性可分。

在非线性情况下，分类超平面为wΦ（x）+b=0。以软间隔为例，求解非线性最优分类超平面可描述为

类似于线性支持向量机，利用拉格朗日乘子法将式（2.121）转化为其对偶问题

根据式（2.122）可知，在高维特征空间中构造最优超平面，只需要知道特征空间中的内积运算即可。由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算Φ（xi）Φ（xj）通常是困难的。如果能找到一个核函数K（·，·），使得K（xi，xj）=〈Φ（xi），Φ（xj）〉。我们就没必要直接去计算高维甚至无穷维特征空间中的内积。满足下面Mercer条件的内积函数K（xi，xj）称为核函数。

Mercer条件：任意给定的对称函数K（xi，xj）是某个特征空间中内积运算的充分必要条件是：对于任意不恒为零的函数g（x），且，有成立。

常用的核函数有：

（1）高斯（Gaussian）核函数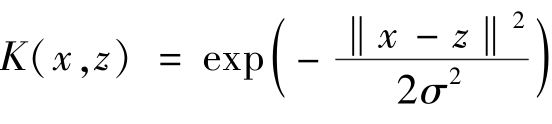：。(www.daowen.com)

（2）多项式核函数：K（x，z）=（x·z+1）p。

（3）拉普拉斯（Laplacian）核函数：。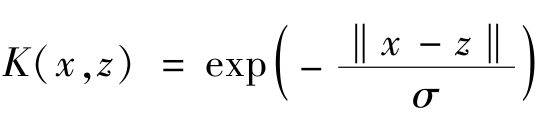

（4）sigmoid核函数：K（x，z）=tanh（γx·z+r）。

支持向量机通过引入核函数成功地将线性分类问题中最优分类面的思想用于非线性问题，实现了较复杂的非线性分类。此时的二次优化问题（2.122）变为

根据Mercer核的性质，核函数替换内积后的二次规划问题仍然是一个凸问题，存在着唯一的全局最优解，而且理论证明由Mercer核生成的再生核希尔伯特空间具备了良好的可分性。应用核函数有效地避免高维空间中的内积计算，并且无须知道映射函数Φ（·）的具体形式。求解后非线性SVM的分类决策函数为