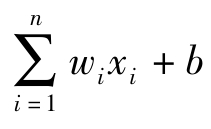图2.1为神经元的数学模型结构，为了模拟神经元的信号传递过程，输入xi在进入神经元之前，需与权重wi相乘，在对加权信号量求和之后加上偏置b，因此该神经元得到的信号为。为了模拟生物神经细胞的兴奋（或抑制）的二元输出，一个常用的方式是在神经元的末尾添加阶跃函数f，即当信号经过神经元时，用阶跃函数对信号做二值化处理，这个函数也称为阈值型激活函数f。这种以阶跃函数模拟神经元的方式在早期被称为“感知器”[4]。经过激活函数后，神经元的输出表示为

为了简单表示式（2.84），可以将偏置b作为神经元权值向量w的第一个分量加到权值向量中，因此可以将输入信号与权重分别记为x=[1　x1　x2　…　xn]T和w=[b　w1　w2　…　wn]T，输入向量x和权值向量w的内积就可以表示激活函数的输入[5]。在学习算法中若要求激活函数可导，可采用sigmoid函数来作为激活函数，将变量映射到区间（0，1）。sigmoid函数的数学表示为

sigmoid函数的优点有：非线性、单调性、无限可导，当权值很大时可以近似为阈值函数，当权值较小时可以近似为线性函数。除了sigmoid函数外，常用的激活函数还有tanh、ReLU（rectified linear unit，修正线性单元）、ELU（exponential linear unit，指数线性单元）、PReLU（parametric rectified linear unit，参数修正线性单元）等，如表2.1所示，这些激活函数各有特点，可以在不同的学习算法和应用场景中发挥各自的优势，因此在设计神经网络时采用何种激活函数也是一个难点。(www.daowen.com)

表2.1　一组激活函数

多个神经元连在一起就构成了神经网络。当神经元以有向无环的方式连接并做一定程度的修改时，就构成了前向神经网络。最简单的前向神经网络是只有一层神经元的感知器，称为单层感知器。