1.旋转不平衡惯性力引起的振动和噪声

旋转机械的振动绝大多数情况是由旋转零部件（即转子系）产生的不平衡惯性力引起的。由于转子系的形状不对称、材质不均匀、毛坯缺陷、热处理变形、加工或装配误差以及与转速有关的变形等原因，使其质量分布不均匀，质心不在旋转轴心线上，当转子旋转时产生不平衡的离心惯性力或离心惯性力矩，从而激励起机械零件振动并产生噪声。

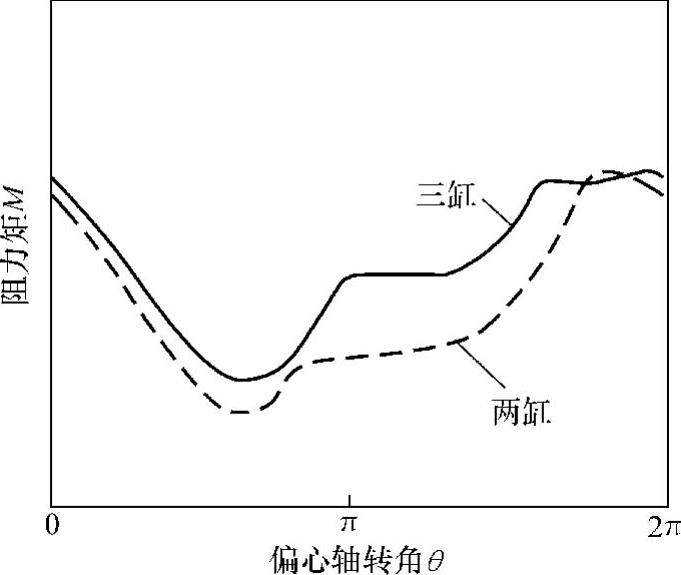
图3.23　两缸及三缸工作模式下的阻力矩曲线图

由于滚动转子式制冷压缩机是一种带有偏心机构的装置，由电机转子、偏心轮轴和滚动转子组成的压缩机转子系在旋转时本身就是不平衡的，所以在运行时会产生不平衡离心惯性力和离心惯性力矩，从而使压缩机产生振动和噪声。

转子系不平衡离心惯性力或离心惯性力矩产生的振动和噪声由基频及其高次谐波组成，其频率的表达式为

式中　f——转子系的不平衡惯性力产生的振动频率，单位为Hz；

n——转子系的转速，单位为r/min；

i——谐波次数，为1，2，3，4，…。

因此，转子系不平衡离心惯性力或离心惯性力矩产生振动和噪声的基频即为压缩机的运转频率。

滚动转子制冷式压缩机转子系不平衡惯性力或离心惯性力矩产生的振动对压缩机整机振动的影响较大，严重时有可能导致制冷剂连接管路断裂。

在滚动转子式制冷压缩机中，虽然不平衡惯性力或离心惯性力矩产生的基频噪声频率不高（变频压缩机运转频率范围一般为5～130Hz），低阶谐波的频率处于人耳不太敏感的区域，但高频运转时，转子系不平衡离心惯性力或离心惯性力矩会产生很大的冲击力，破坏其他零部件（如轴承等）的平稳工作状态，产生高频振动和噪声。也就是说，这种噪声源本身往往不辐射空气噪声，而主要是作为振动的能源，通过轴承、气缸等传递路径传递到压缩机壳体上，迫使壳体振动辐射出空气噪声。

当压缩机零件的某一阶固有频率与转子系基频或谐波频率相等或接近时，将产生较大的共振噪声。因此，转子系的不平衡才是真正的噪声源。

2.控制不平衡力的一般方法

惯性力和惯性力矩将引起转子系支承的动反力和振动，增大轴承负荷并产生噪声。为了减小动反力和振动，降低由转子系激励的振动和噪声，必须使压缩机转子系的惯性力和惯性力矩得到平衡。

所谓的“平衡”是指在转子系上选定适当的校正平面，加上适当的校正质量（或校正质量组），使得转子系的振动和动反力减小到某个允许值以下的过程。

如果设转子系绕z轴转动，则将各质点不平衡惯性力向任意一点简化，可得到一个力R₀和一个力矩M₀，其大小为

式中　m_c——转子系质量，单位为kg；

r_c——质心c到z轴的距离，单位为m；

ω——转子系的角速度，单位为rad/s；

I_xz，I_yz——转子系的转动惯量（惯性积），单位为kg·m²。

平衡应满足的条件是

1）R₀=0，即r_c=0；

2）M₀=0，即I_xz=0，I_yz=0。

满足条件1），则应使z轴通过质心，满足条件2），则z轴是主惯性轴之一，所以平衡应满足的条件是转轴z为中心主惯性轴之一。

滚动转子制冷压缩机的结构特性决定了转子系本身是不可能平衡的，需要用配置平衡配重块的方法来平衡。

3.平衡块配置

在滚动转子制冷压缩机中，由于受到结构的限制，转子系的平衡配重块只能设置在电机转子的端部。为了使惯性力和惯性力矩完全平衡，通常在电机转子的两端面配置两个平衡配重块。

双级压缩变容积比压缩机的三个气缸是非对称的，即偏心轮轴上的三个偏心质量（包括滚动转子）、偏心距都有可能不相同，并且，偏心质量的布置也有多种方式，有在同一个平面的布置方法（三个偏心质量在一个平面上布置），也有不在同一个平面的布置方法。

下面以图3.24和图3.25所示三个偏心质量质心在同一个平面的布置方法为例来说明平衡块的配置和计算方法。图中m_x为偏心质量，r_x为偏心距。

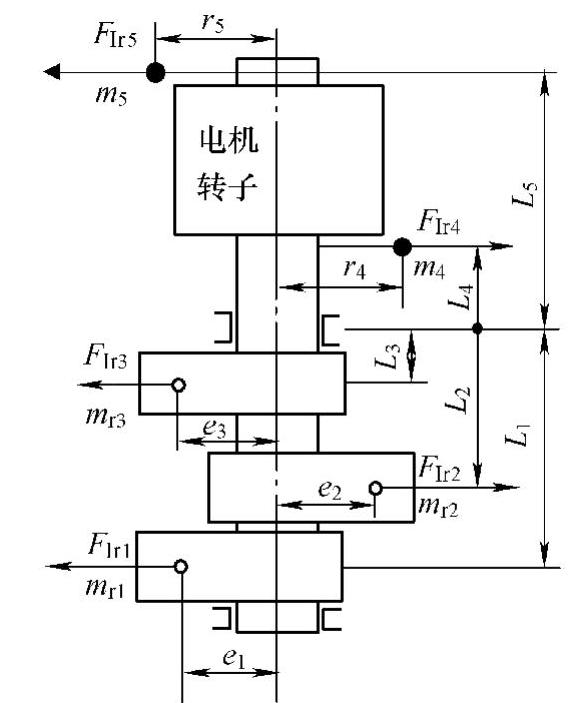
图3.24　三缸转子系旋转惯性力及力矩平衡Ⅰ

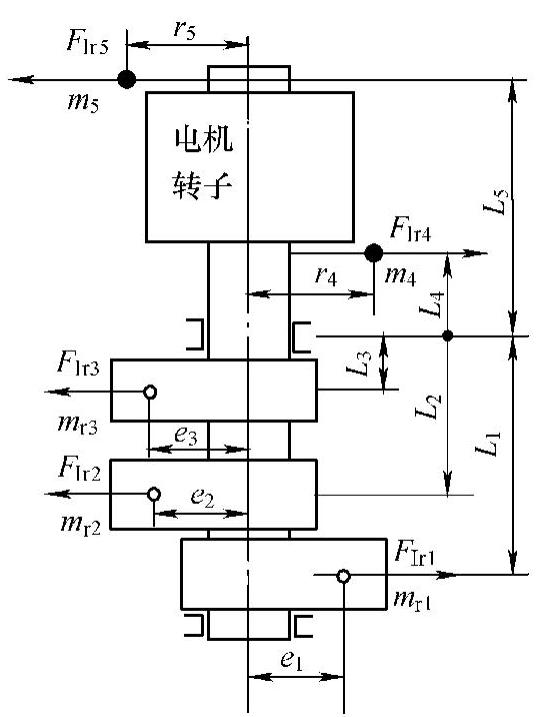
图3.25　三缸转子系旋转惯性力及力矩平衡Ⅱ(www.daowen.com)

在图3.24中，力平衡为

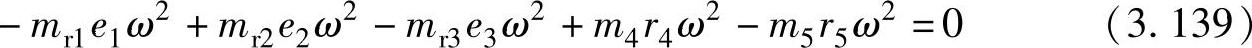
力矩平衡（取顺时针方向为力矩的正方向，以下偏心质心作为力矩平衡点，下同）为

-m_r1e₁ω²L₁+m_r2e₂ω²L₂-m_r3e₃ω²L₃-m₄r₄ω²L₄+m₅r₅ω²L₅=0 （3.140）

由式（3.139）和式（3.140）有

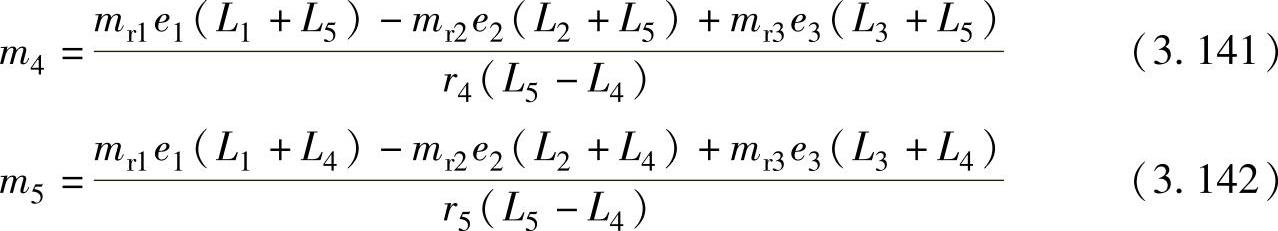
在图3.25中，力平衡为

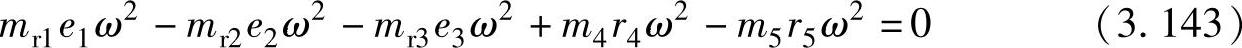
力矩平衡为

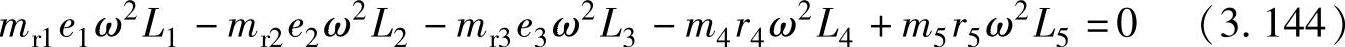
由式（3.143）和式（3.144）有

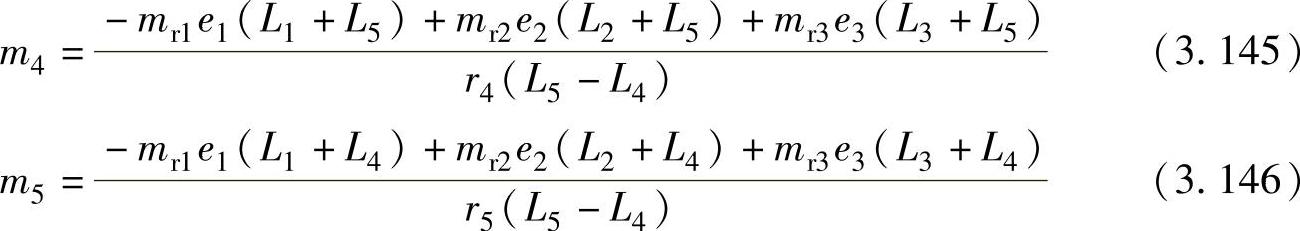
在上述压缩机转子系平衡方法的计算中，假设转子系为刚性。而在实际中，当压缩机高速运转时，转子系具有一定的挠度，即转子系是挠曲的。采用上述一般平衡方法并不能保证转子系离心惯性力最小，仍然有可能会导致压缩机高速运行时产生较大的振动和噪声。

为了确保压缩机高速运转时转子系的平稳性，转子系的动平衡性能需考虑偏心轮轴挠度的影响，进行平衡设计时必须考虑偏心轮轴的变形，才能有效减少不平衡离心惯性力和力矩作用下的振动幅值和噪声。

接下来介绍考虑偏心轮轴挠度的压缩机转子系平衡的设计方法。进行静平衡计算时，由于偏心轮轴偏心部、主副平衡块和电机转子因挠度产生的离心力与挠度的乘积非常小，故可忽略挠度的影响。在进行动平衡计算时，由于偏心轮轴偏心部、主副平衡块因挠度产生的附加离心力矩远小于电机转子因挠度产生的附加离心力矩，故可忽略偏心轮轴偏心部和主副平衡块因挠度产生的附加离心力矩的影响。

因此，在考虑偏心轮轴挠度的转子系平衡的设计方法中，只考虑转子挠度产生的附加力矩对动平衡的影响就可得到比较满意的结果，这样既简化了平衡计算过程，又可评估挠度对平衡带来的影响。

下面以图3.25所示偏心轮轴为例对考虑偏心轮轴挠度的转子系平衡设计方法进行说明。考虑偏心轮轴挠度的压缩机转子系平衡系统如图3.26所示。

力平衡（忽略电动机转子因挠度产生的离心力）为

m_r1e₁ω²-m_r2e₂ω²-m_r3e₃ω²+m₄r₄ω²-m₅r₅ω²=0 （3.147）

力矩平衡为

m_r1e₁ω²L₁-m_r2e₂ω²L₂-m_r3e₃ω²L₃-m₄r₄ω²L₄+m₅r₅ω²L₅+m_rδ_rω²L_r=0 （3.148）

式中　m_r——电机转子的质量，单位为kg；

δ_r——电机转子质心因轴挠曲产生的偏心量，单位为m；

L_r——电机转子质心到转矩中心的距离，单位为m。

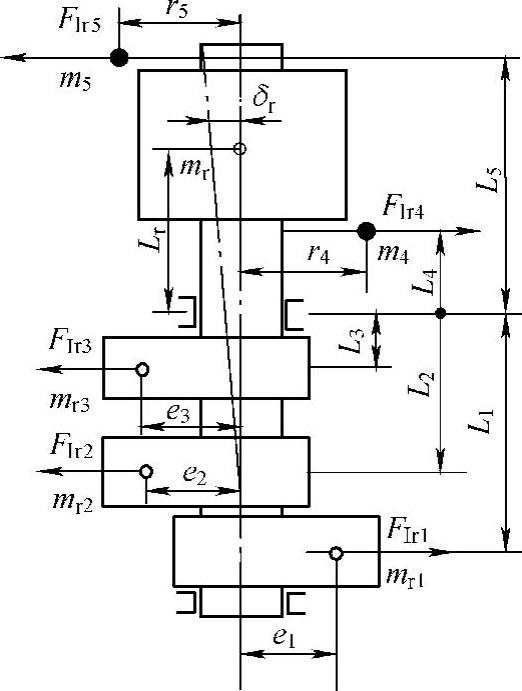
图3.26　考虑挠度的转子系平衡系统

由于偏心轮轴结构复杂，因此需要在一般平衡法的力平衡和力矩平衡基础上采用有限元分析法计算偏心轮轴的挠度，将有限元计算的挠度结果迭代入平衡方程中，进行循环计算，直到计算得到合理的平衡质量及挠度值。计算流程框图如图3.27所示。

为了对平衡性能评估，引入静平衡系数和动平衡系数，其定义式如下：

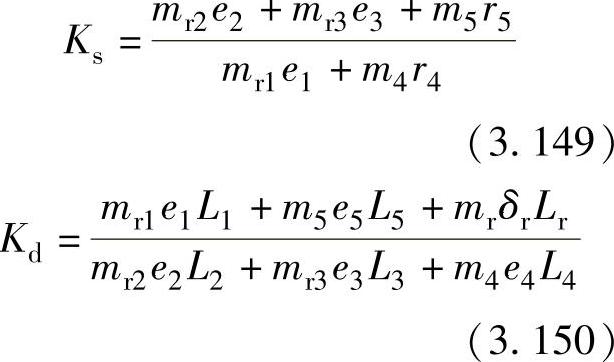
式中　K_s——静平衡系数；

K_d——动平衡系数。

通过多次的循环迭代计算，考虑电机转子因偏心轮轴的挠度产生不平衡块惯性力矩的影响，最终进行转子系平衡块配重的设计后，静平衡系数K_j、动平衡系数K_d的值应近似等于1。

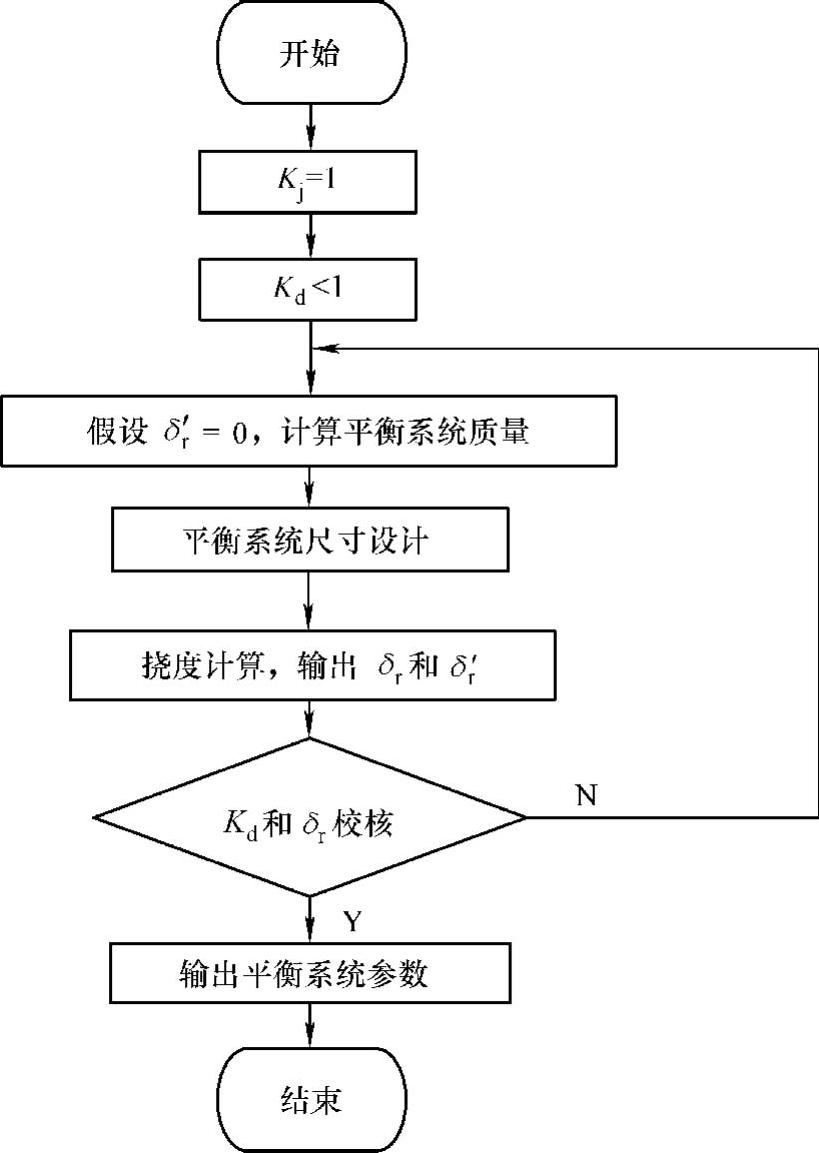
图3.27　转子系平衡计算流程图