1.气缸工作容积的变化规律

滚动转子式制冷压缩机气缸工作腔的几何关系如图3.13所示。在图3.13中，O点为气缸中心，O₁为滚动转子中心，气缸中心和滚动转子中心的连线OO₁表示滚动转子或偏心轮轴所处的位置。设OO₁与滑片中心线重合时作为偏心轮轴转角的开始点，即偏心轮轴的转角θ为0°。

从图3.13中可以得到以下几何关系：

r²=e²+R²_θ-2eR_θcos（θ-ϕ） （3.1）

式中　r——滚动转子的半径，单位为m；

e——偏心距，即滚动转子中心与气缸中心的距离，单位为m；

θ——滚动转子的转角，单位为rad；

ϕ——0°～θ之间的任意角度，单位为rad；

R_θ——任意角度ϕ时气缸中心至滚动转子外圆的距离，单位为m。

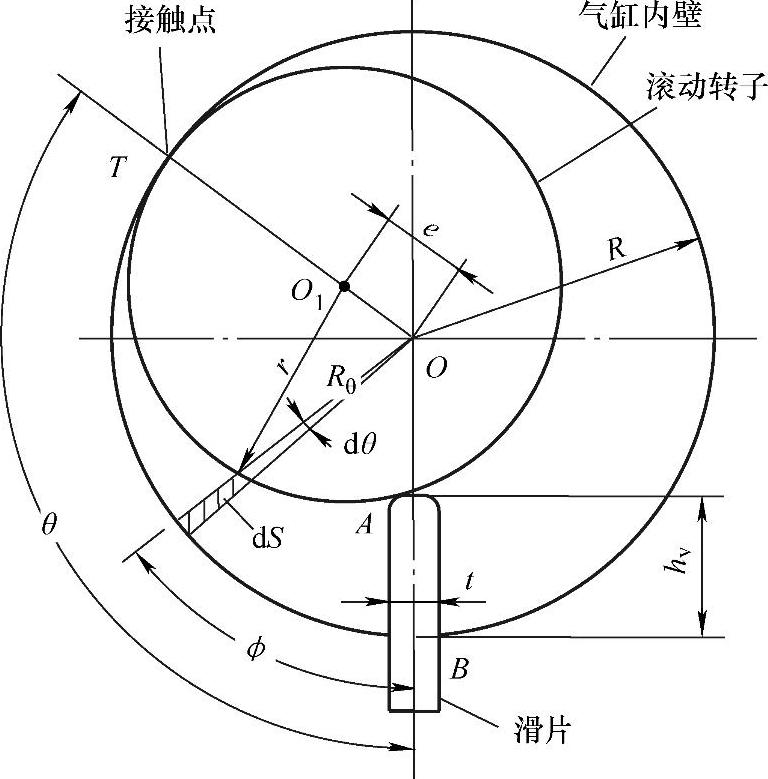
图3.13　气缸工作腔的几何关系

求解式（3.1），可以得到

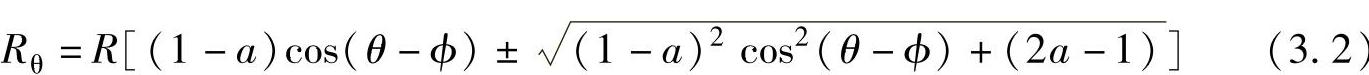
式中　R——气缸的半径，单位为m；

a——滚动转子与气缸的半径比，a=r/R。

在实际气缸结构中，式（3.2）中的半径比a都略小于1，（2a-1）始终为正，因此，中括号内第二项的数值总是大于第一项的数值，根号前取负号无意义，忽略负号，可以得到

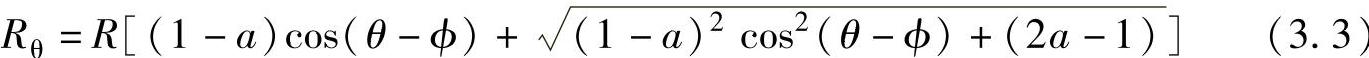
为了确定工作腔的截面积，在任意转角θ时，取图3.13所示的面积微元dS分析，有

如果不考虑滑片厚度的影响，则在任意转角θ处，由气缸内表面、滚动转子外表面及滑片所围成工作腔的截面积为

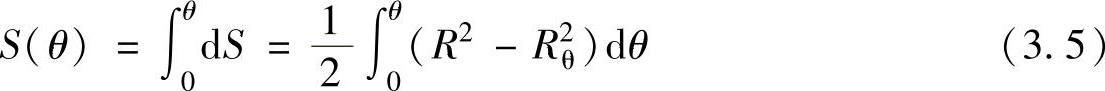
将式（3.3）代入式（3.5）并积分，有

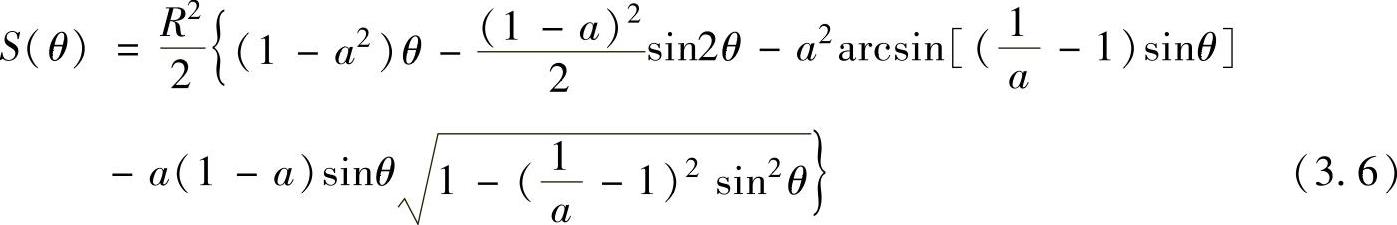
将式（3.6）表示为

式中

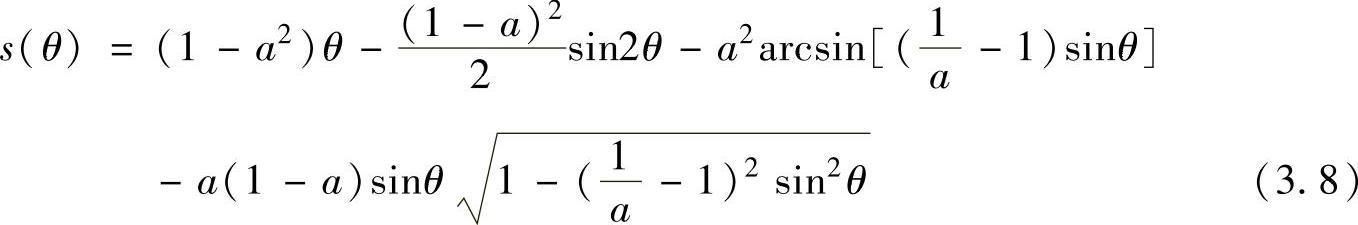
则工作腔的容积V（θ）为

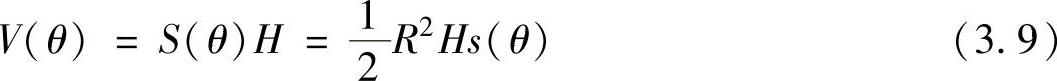
式中　H——气缸的高度，单位为m。

当θ=2π，即滚动转子将滑片全部推出气缸之外时，整个工作腔充满了吸入的制冷剂气体，此时的气缸容积称为压缩机的气缸工作容积，用V_t表示，有

V_t=π（R²-r²）H （3.10）

在任意转角θ时，滑片将整个工作容积分成两部分，即吸气腔容积V_s和压缩腔容积V_c，显然(www.daowen.com)

V_t=V_s+V_c （3.11）

到目前为止，上述讨论中一直未考虑滑片厚度的影响。当考虑滑片厚度的影响时，任意转角的吸气腔容积为

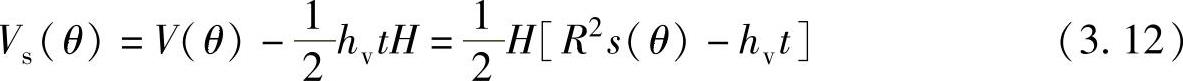
式中　t——滑片的厚度，单位为m；

h_v——滑片伸到气缸内的长度，单位为m。

如图3.13所示，滑片伸到气缸内的长度为

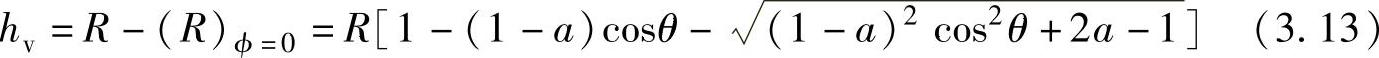
在任意转角时压缩腔的容积为

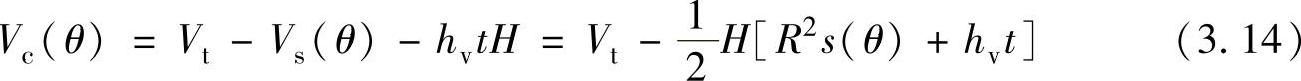
2.工作腔内气体的压力

气缸工作腔内气体的压力变化可以根据各工作过程的多方指数和工作腔容积的变化规律求出。

（1）吸气过程

由于滚动转子式制冷压缩机没有吸气阀，所以在吸气过程中气体的压力损失很小，可近似认为吸气腔内气体的压力p_b与吸气管路内的压力p_s相同，即

p_b=p_s （3.15）

（2）压缩过程

在滚动转子式制冷压缩机中，气缸是通过偏心轮轴旋转两圈来完成工作过程的，在第二圈开始压缩过程。第二圈的压缩过程主要分为三个阶段。

第一个阶段为滚动转子转至吸气孔口前边缘角β（见图3.4）之前，即θ=2π+β，压缩腔与吸气管路相通，此时未对气体产生压缩，气缸内的气体压力为吸气管中的压力，即

p_θ=p_s （3.16）

第二个阶段为滚动转子转过吸气孔口前缘角之后至排气阀阀片打开之前的区域，即2π+β<θ<2π+ψ。在此旋转角度范围内，气缸工作腔的压力随着偏心轮轴转角的增大而升高。假设压缩过程是指数为m的多方过程（pV^m=常数），此时压缩腔内的压力与容积之间满足过程方程，则有

p_θV^mθ=p_sV^m_β （3.17）

式中　V_θ——转角为θ时的基元容积值，单位为m³；

V_β——压缩开始瞬时（θ=2π+β）的基元容积值，单位为m³；

p_θ——转角为θ时基元容积内的气体压力值，单位为Pa；

p_s——吸气压力，单位为Pa。

因此，对应于转角θ的气体压力为

如果不考虑滑片的厚度，则运算后可以得到

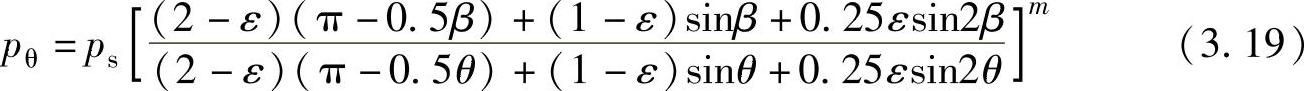
式中　ε——相对偏心距，ε=e/R。

第三个阶段为排气开始后，压缩腔内的压力假设由p′_d随转角θ线性地减少至排气压力p_d，于是压缩腔内的压力变化可表示为

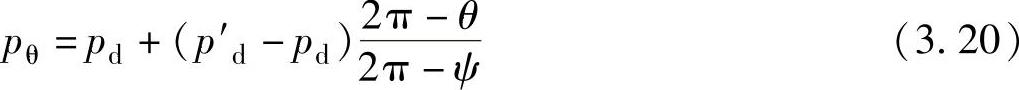
式中　p′_d——气缸排气前压缩腔的压力，单位为Pa。