从2.3.1节中的理论分析可知，影响双级压缩循环性能的因素很多，其中，双级压缩的容积比是影响性能最关键的因素之一。因此，在双级压缩循环系统中，合理确定高压级与低压级的容积比是设计关键。

所谓最优容积比，是指双级压缩循环系统在工况条件一定的情况下，制冷EER或者制热COP最高时的高压级气缸工作容积与低压级气缸工作容积之比，最优容积比用R_v，opt表示。

在实际的双级压缩空气源热泵循环系统中，由于受到环境温度、制冷剂流动阻力、换热条件等各种因素的影响，双级压缩循环的参数是变化的。为了便于分析，做以下假设：

1）在冷凝器和蒸发器中，不计流动压降，相应的冷凝温度和蒸发温度不变；

2）制冷剂在管路内流动时，不计流动压降；

3）制冷剂流过节流装置时，与外界环境没有换热；

4）低压级的气缸容积效率与高压级的气缸容积效率相等。

模拟计算时，假设计算参数如下：

1）高压级和低压级的热力等熵效率为0.7；

2）冷凝器出口过冷度为5℃；

3）吸气过热度为0℃；

4）中间补气液体携带率为0；

5）冷凝温度计算范围为25～65℃；

6）蒸发温度计算范围为-50～30℃。

在上述假设条件下，选取R-410A、R-290、R-22、R-32和R-134a这五种制冷剂作为研究对象，分别计算和分析双级压缩循环的最优容积比，以及相对单级压缩循环COP提高的幅度等。

1.R-410A的最优容积比

首先研究R-410A制冷剂的最优容积比。

当冷凝温度分别为25℃、35℃、45℃、55℃、65℃时，计算得到的R-410A最优容积比随着蒸发温度和冷凝蒸发温度差的变化曲线分别如图2.11a和b所示。

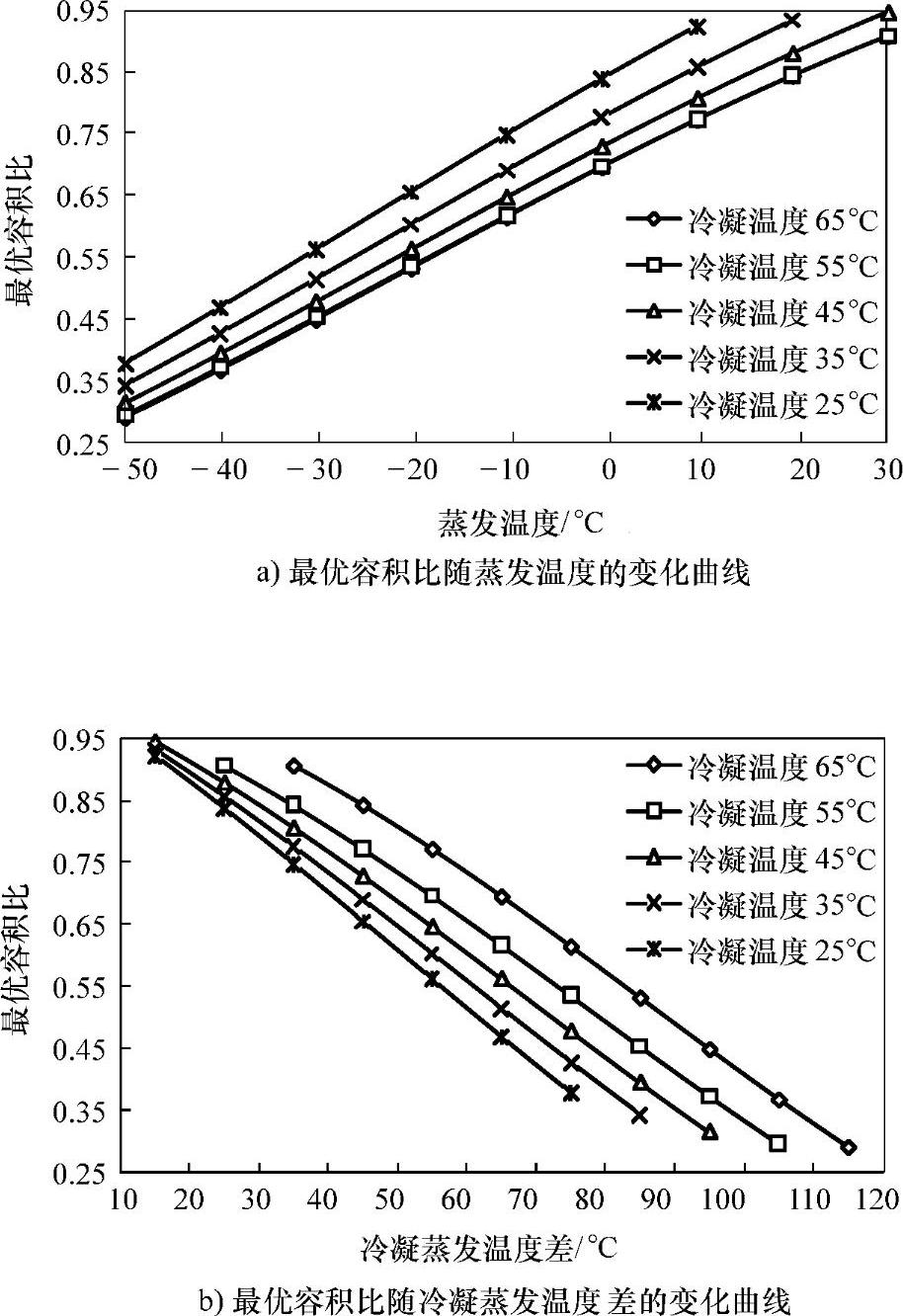
图2.11　R-410A最优容积比曲线

从图2.11a中可以看出，当冷凝温度一定时，最优容积比随着蒸发温度的降低近似呈线性减小，即蒸发温度越低，最优容积比越小。例如，当冷凝温度为45℃，而蒸发温度从30℃降至-50℃时，最优容积比从0.94减小至0.31。当蒸发温度一定时，最优容积比随着冷凝温度的升高而减小，且减小的速度随着蒸发温度的降低而变慢，即图2.11a中的曲线变得越来越密集。

从图2.11b中可见，当冷凝温度与蒸发温度之差一定时，最优容积比随着冷凝温度升高而增大；当冷凝温度一定时，最优容积比随着冷凝温度与蒸发温度之差的增大近似呈线性减小。

2.最优容积比与制冷剂关系

由式（2.55）可知，容积比与制冷剂的物性相关，因此，最优容积比的大小必然与制冷剂的类型相关。

将计算得到的R-290、R-32、R-22和R-134a这四种制冷剂的最优容积比与R-410A的最优容积比进行比较，比较结果分别如图2.12～图2.15所示。(www.daowen.com)

从图2.12和图2.13中可以看出，当冷凝温度在25～55℃范围内时，R-290和R-32的最优容积比与R-410A的最优容积比十分接近，与R-410A最优容积比的相对值在0.96～1.03范围内；当冷凝温度为65℃时，与R-410A最优容积比的相对值在0.92～0.96范围内。

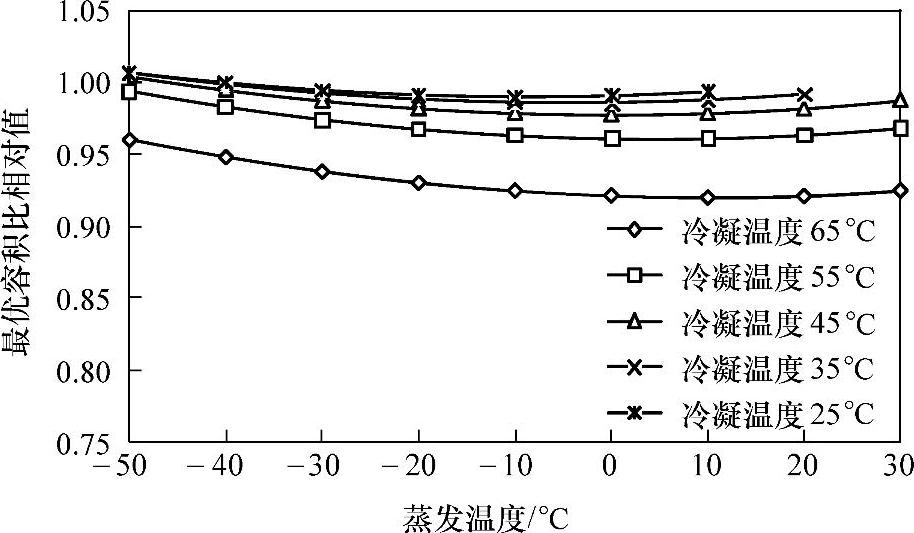
图2.12　R-290与R-410A最优容积比的相对值

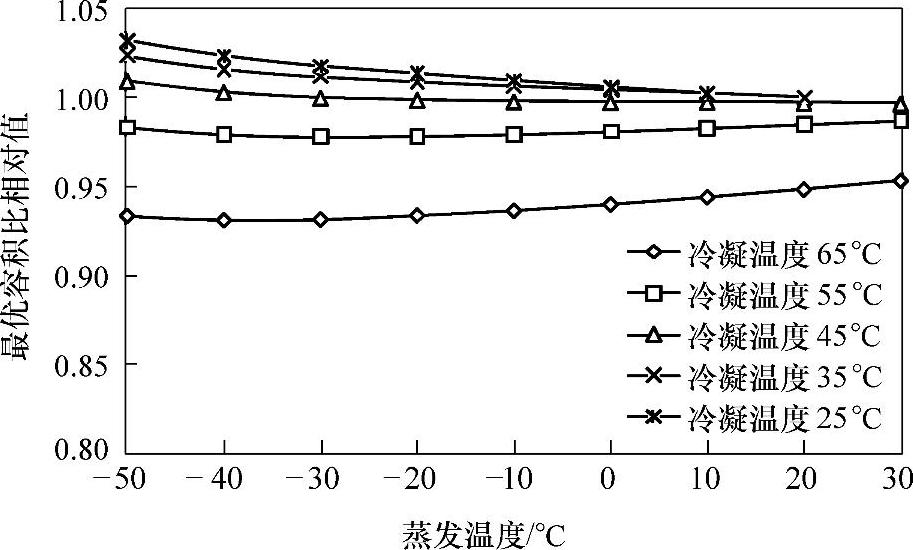
图2.13　R-32与R-410A最优容积比的相对值

从图2.14和图2.15中可以看出，制冷剂R-22和R-134a最优容积比与制冷剂R-410A最优容积比的相对值均小于1，并且随着蒸发温度的降低或冷凝温度的升高而减小。在上述五种制冷剂中，在相同工况条件下，制冷剂R-134a的最优容积比最小。

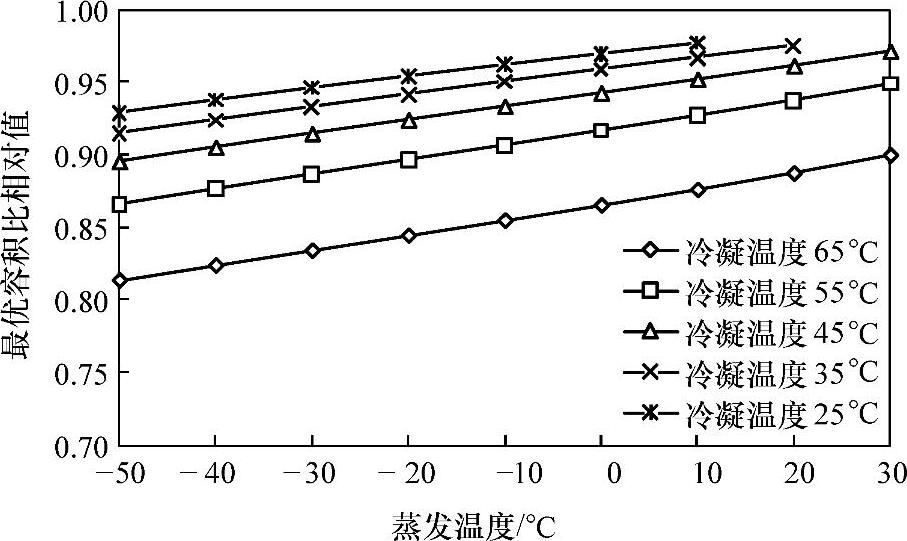
图2.14　R-22与R-410A最优容积比的相对值

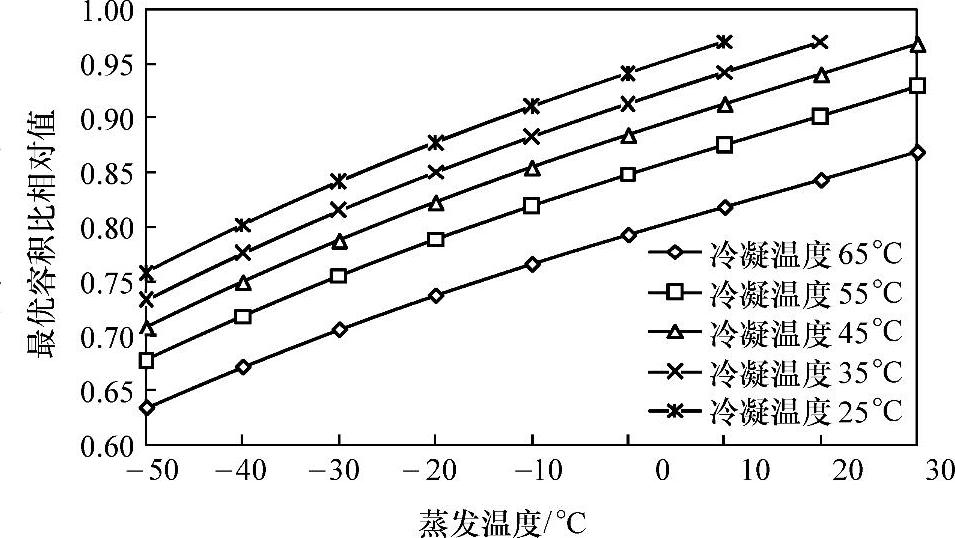
图2.15　R-134a与R-410A最优容积比的相对值

R-290、R-32和R-410A双级压缩循环的理论最优容积比在计算工况范围内可以采用式（2.59）所示的拟合关联式。在本节计算工况范围内，该关联式的预测值与理论最优容积比计算值的平均相对偏差对于R-290、R-32和R-410A分别为1.0%、1.7%和2.8%，最大相对偏差对于R-290、R-32和R-410A分别为4.6%、5.2%和7.7%。

R_v，opt=（c₀+c₁t_e+c₂t_c+c₃t_et_c+c₄t²_e+c₅t²_c）（c₆+c₇Δt_sc/t_c） （2.59）

式中　t_e——蒸发温度，单位为℃；

t_c——冷凝温度，单位为℃；

Δt_sc——冷出过冷度，单位为℃；

c_i——系数，其中，c₀=0.98596，c₁=9.3684×10^-3，c₂=-9.1383×10^-3，c₃=-3.9061×10^-5，c₄=-6.0952×10^-6，c₅=5.6071×10^-5，c₆=0.99995，c₇=0.28089。

3.最优COP与对应的容积制热量相对于单级压缩提高幅度

R-410A、R-290、R-134a、R-22和R-32五种制冷剂在双级压缩循环中的最优COP，以及对应容积制热量相对单级压缩循环提高幅度分别如图2.16～图2.20所示。

从图2.16～图2.20中可以看出，采用这五种制冷剂的双级压缩循环的最优COP，相对应的容积制热量以及相对单级压缩循环的提高幅度均随蒸发温度降低和冷凝温度升高而增大。在相同计算工况条件下，R-410A、R-290和R-134a的最优COP提高幅度较大，R-22的最优COP提高幅度次之，R-32的最优COP提高幅度最小，相应的容积制热量提高幅度与COP提高幅度大致也是这一顺序。例如，冷凝温度为45℃且蒸发温度为-30℃时，R-410A、R-290、R-134a、R-22和R-32的最优COP提高幅度依次为10.5%、11%、10.9%、7.4%和6.4%，相对应的容积制热量提高幅度依次为33.2%、32.3%、31.9%、24.9%和24%。

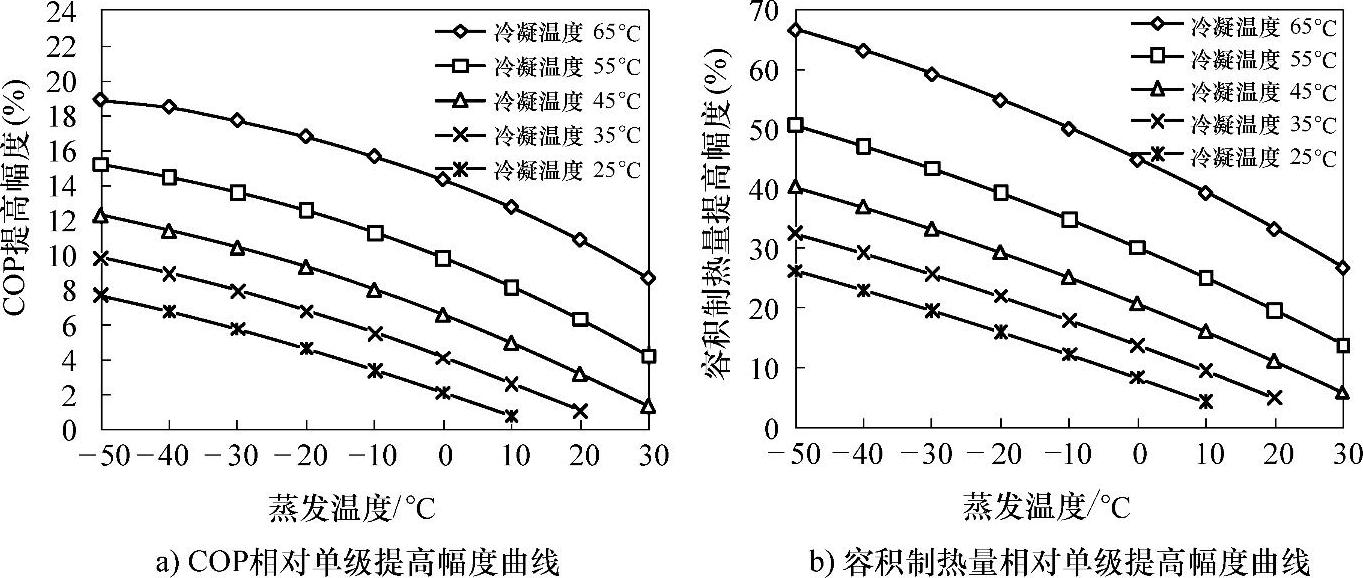
图2.16　R-410ACOP和容积制热量相对单级提高幅度曲线

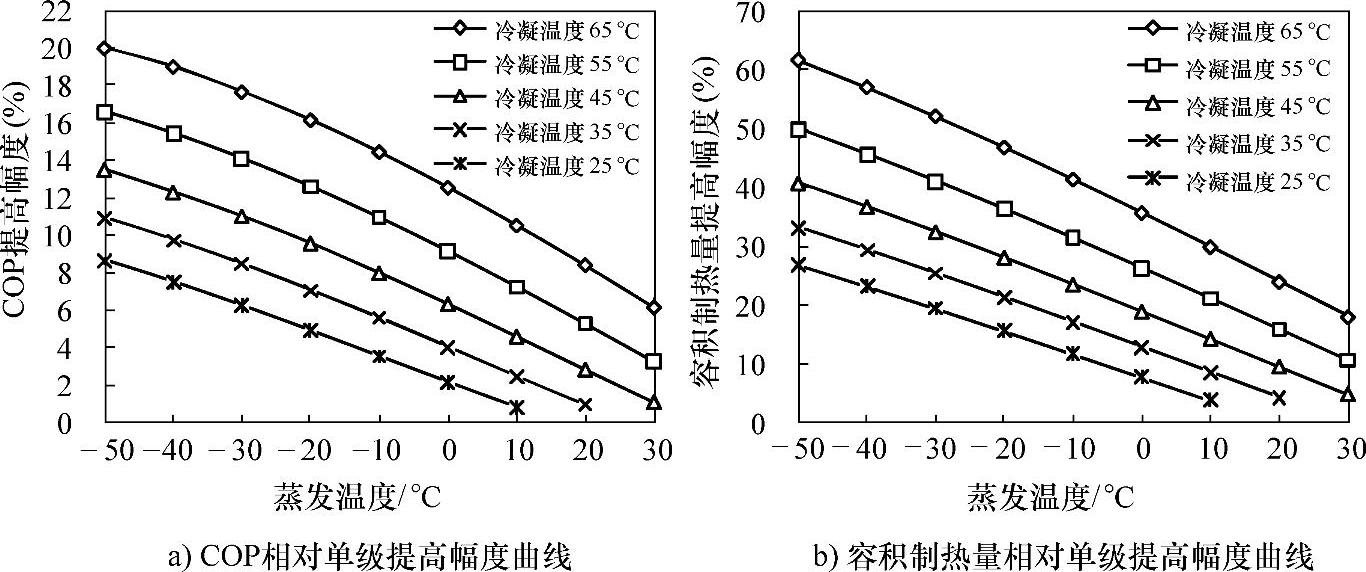
图2.17　R-290COP和容积制热量相对单级提高幅度曲线