协调运动控制是指，当控制对象在多轴上运动时，多轴间的位移进行协调，以使控制对象能按预定的轨迹运动。

达到协调运动控制有两个方法：一是直线圆弧插补法，另一是直接目标跟踪法。

直线圆弧插补法常见的是把要求的运动轨迹分解为若干小段的直线或圆弧。而每小段直线或圆弧轨迹则运用一定算法，控制对象在不同轴上一步步位移予以实现。常用的算法有逐点比较法、累加法等。

如果运动轨迹可用数学方程式表示，也可直接目标跟踪法进行控制。它运用数学方程式直接进行计算，然后控制对象在不同轴上一步步位移予以实现。

协调运动控制也称连续轨迹控制。在数控车、铣床，雕刻机、激光切割机、激光焊接机、激光雕刻机、数控冲压机床、快速成型机、超声焊接机、火焰切割机、等离子切割机、水射流切割机等都有它的应用。

以下分别对直线插补、圆弧插补、直接目标跟踪、相对值数据列表运动控制及绝对值数据列表运动控制进行介绍。

1.直线圆弧插补法

（1）直线插补法。

1）直线插补算法：直线插补的算法很多。这里介绍的是基准轴输出为主，辅助轴输出配合半累加插补算法。此算法使用时，起始点为当前位置，终点可按直角坐标的X、Y值，以脉冲为单位选定。同时，还要选定所在象限。用选定象限确定脉冲输出的方向。如第一象限，则X为正向，Y也为正向。如二象限，则X为反向，Y为正向。其他象限类推。在执行程序时按步计算，按步输出脉冲，而方向用方向信号控制。

所谓基准轴，就是终点坐标值较大的轴。每一步它都输出脉冲，只是当辅助轴有脉冲输出时，它先让辅助轴输出，而在后一个周期，它才输出。辅助轴是否输出，用累加的方法确定。

累加的过程是，用自身的终点坐标累加，当大于基准轴的终点坐标时，输出一个脉冲，并把累加值被基准轴的终点值减，其“差”又作为在累加值存储。该算法的框图如图4-70所示。

图4-71所示为一个插补运算实例。

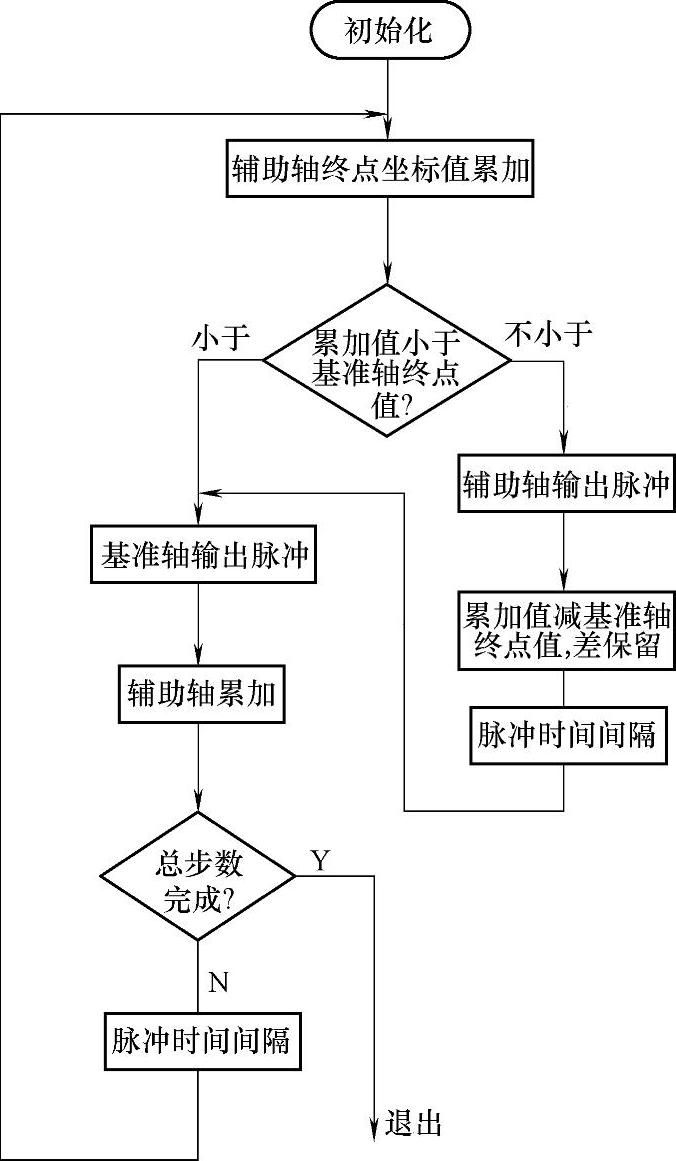
图4-70 半累加直线插补算法框图

从图4-71可知，该例的X轴终点坐标为9，而Y轴为3。可知，应选X轴为基准轴，而Y为辅助轴。从图4-71可知，一开始就累加辅助轴的终点坐标值。但它仅3，比基准的终点坐标值9小，故仅基准轴输出脉冲，走第1步。接着，又累加辅助轴的终点坐标值。这时累加值为6，比基准的终点坐标值9小，故仅基准轴输出脉冲，走第2步。接着，又累加辅助轴的终点坐标值。这时为9，不比基准的终点坐标值9小，故仅辅助轴输出脉冲，走第3步。进而累计值被基准轴的终点值减，其“差”为0，并以0作为新的累加值。之后如图示，4、5、6又是X轴输出；7是Y轴输出；8、9、10又是X轴输出；11是Y轴输出；12又是X轴输出。

可知，本算法的进给的速度是恒定的，这有利于在切削加工中应用。

2）直线插补算法程序实现：程序是按算法编的，也是算法的具体化。其基本程序如图4-72～图4-74所示。图4-72为步进工作起动及初始化程序。图4-73为X是基准轴时的脉冲输出控制程序。至于Y是基准轴时的脉冲输出控制程序与此类似，故不重复。图4-74为终点及方向控制程序。这里方向控制，仅针对两个象限，其他两个象限略。

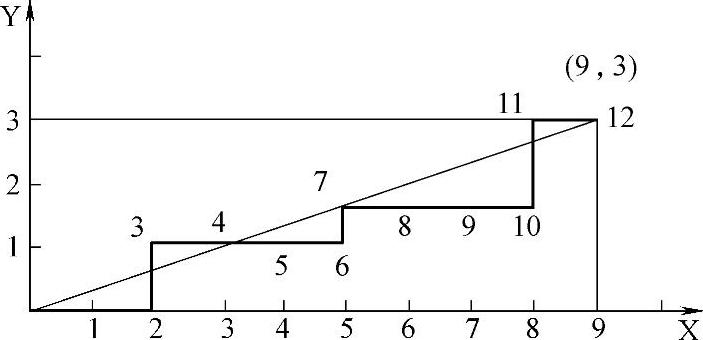
图4-71 插补运算实例

PLC的步进起动程序都是用了基本的起、保、停逻辑。“步进起动”ON，则“步进工作”ON，并自保持。直到“步进完成”ON其常闭闭点把“步进工作”OFF。这里并联“再起动”，为了选定新的程序后重起动的需要。

这初始化程序则多是微分执行的。其功能是判断那个轴为基准轴、传送坐标值及使参数回到初始值。显然，不进行初始化，程序是无法正确执行的。

另外，还要起动定时器TIMH000（图4-75a）、T100或T200（图4-75c）。按图设定，它每0.05秒ON一个扫描周期。正是用它控制脉冲输出的节奏，即频率。此定时时间可按需要改设。为了控制准确也可启用PLC的定时中断及“立即I/O”刷新的功能，以提高控制效果。

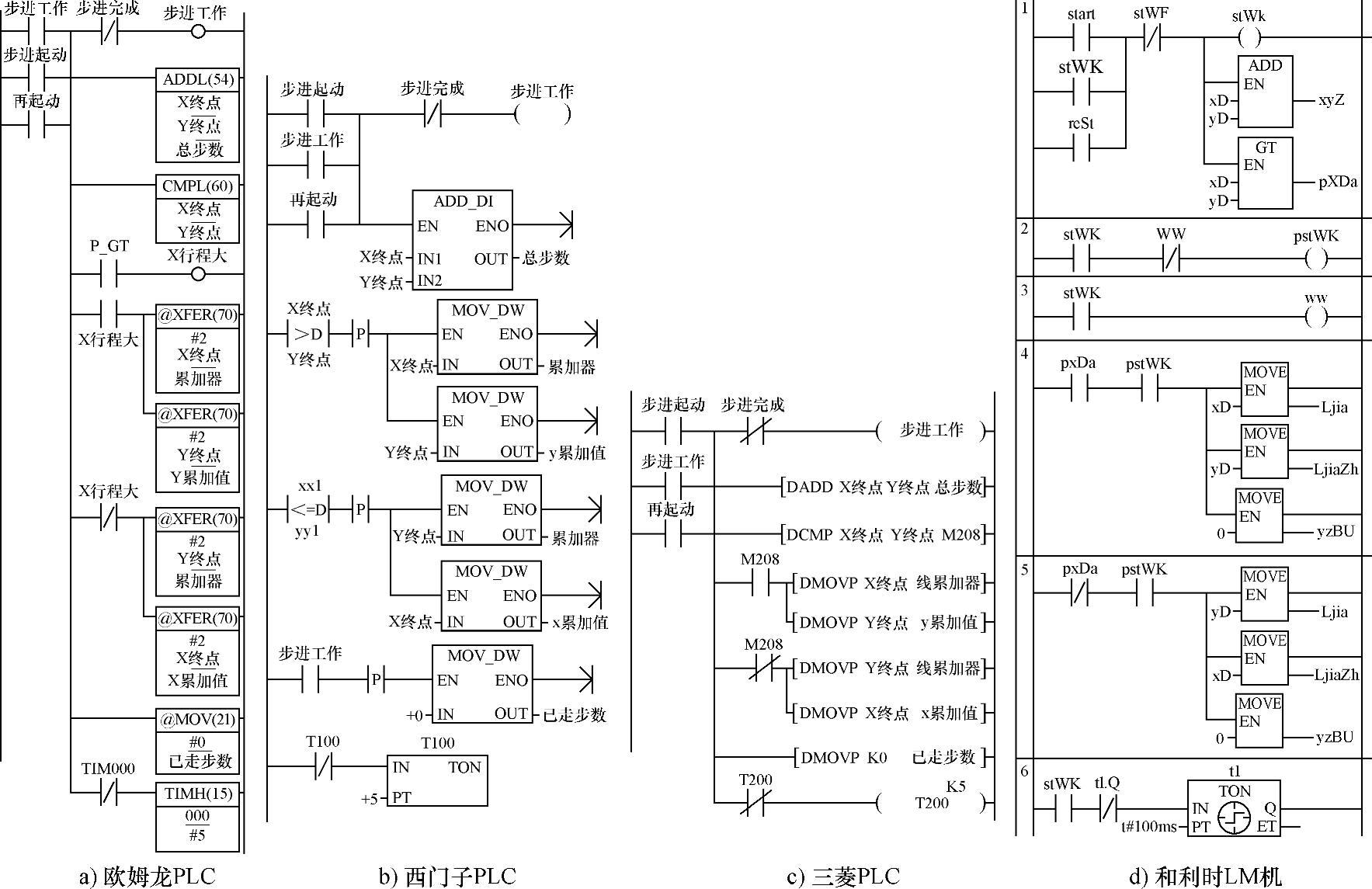
图4-72 步进工作起动及初始化程序

图4-72d为和利时LM机程序。图中节1为步进起动程序，它用了基本的起、保、停逻辑。“start”（步进起动）ON，则“stWK”（步进工作）ON，并自保持。直到“stWF”（步进完成）ON其常闭触点把“步进工作”OFF。这里并联“rest”（再起动），是为了选定新的程序后重起动的需要。

这一初始化程序则多是微分执行的。节2、3是为了产生微分信号“pstWK”。

节4、5功能是判断那个轴为基准轴、传送坐标值及使参数回到初始值。为程序正确执行做好准备。

另外，在节6，起动定时功能块t1。按图设定，它每100msON一个扫描周期。正是用它控制脉冲输出的节奏，即频率。此定时时间可以按照需要改设。为了控制准确也可以启用PLC的定时中断，以提高控制效果。

图4-73所示为PLC当X是基准轴时，脉冲输出控制的梯形图程序。

图4-73a为欧姆龙PLC程序。如图中“X行程大”ON，意味着X为基准轴。正如算法框图指出的，它先把“y累加值”加“y终点”，其“和”赋值给“y累加值”。然后，把“y累加值”被“累加器”减，其“差”赋值给“Y-TEM”。参看图4-73a知，此“累加器”即为X轴的终点坐标值。如不够减，即它小于“累加器”，则“y加进位”OFF，X轴输出脉冲。如足够减，即它大、等于“累加器”，则“y加进位”置位。进而，把“Y-TEM”，即这个“差”赋值给“y累加值”，“y步进”置位，输出脉冲。同时，把“y已输出”置位。“y已走”置位的目的是，在这个工作周期，不让X轴输出脉冲。但临退出本程序段时，用“y加进位”ON，把“y已输出”复位。为下一周期执行X轴发送脉冲做准备。

当下一次再进入本程序段时，由于“y加进位”仍为ON，故Y轴的累加不进行。而使“X步进”置位，进行X方向步进，同时使“y加进位”复位，为新一次的Y轴累加及相应操作做准备。

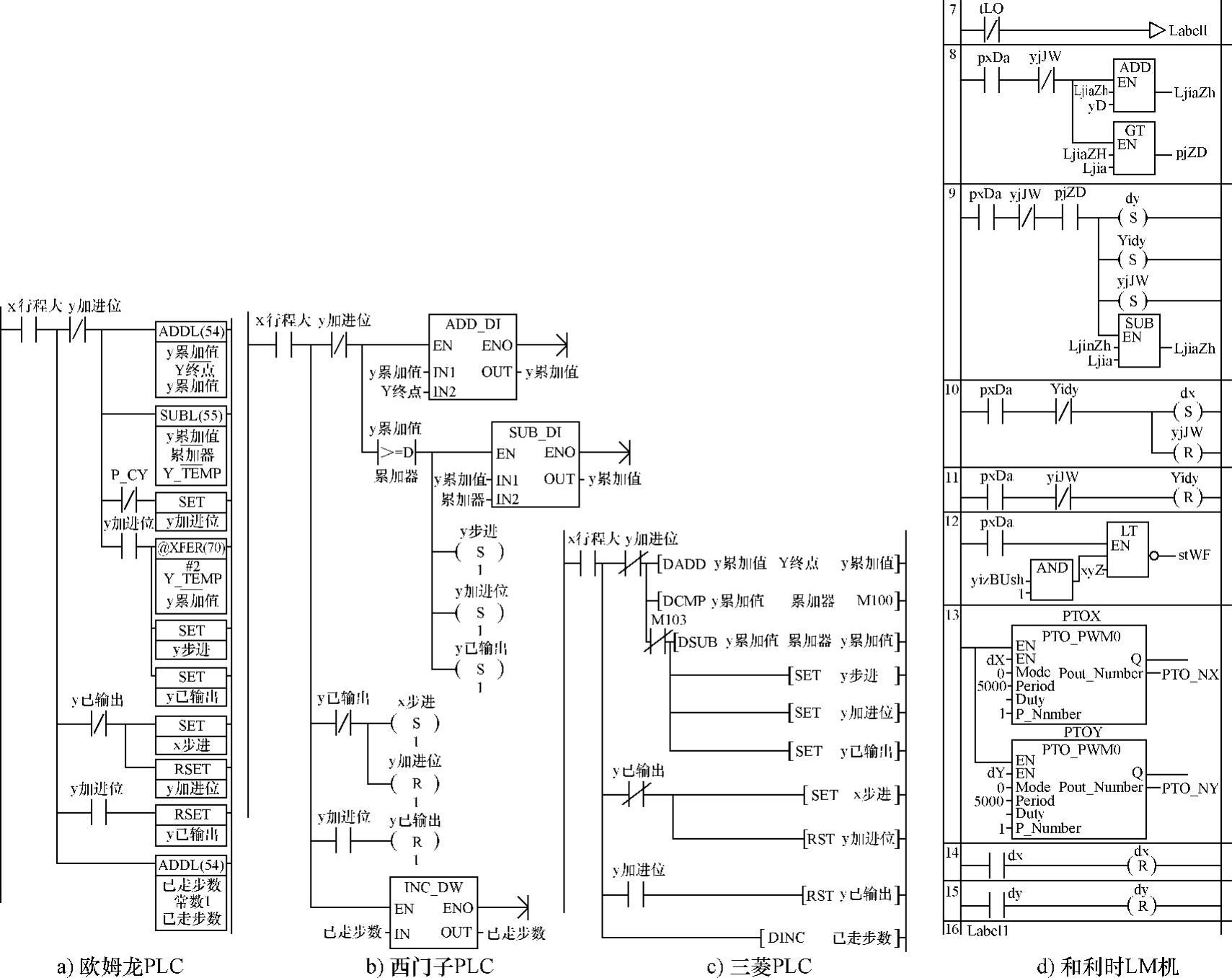
图4-73 X是基准轴时脉冲输出控制

图4-73b为西门子PLC程序。图4-73c为三菱PLC程序。它们用的数据都是用带符号位的十六进制格式，再都用符号地址表示，程序差别不大。

如图中“X行程大”ON，意味着X为基准轴。正如算法框图指出的，它先把“y累加值”加“y终点”，其“和”赋值给“y累加值”。然后，把“y累加值”与“累加器”比较。参看图4-72a知，此“累加器”即为X轴的终点坐标值。如“y累加值”小于“累加器”（即对图4-73c，比较标志M103 ON）则“y加进位”OFF，X轴输出脉冲。如大、等于“累加器”，则把“y累加值”被“累加器”减，其“差”赋值给“y累加值”，“y步进”置位，输出脉冲。同时，把“y已输出”置位。“y已输出”置位的目的是，在这个工作周期，不让X轴输出脉冲。但临退出本程序段时，用“y加进位”ON，把“y已输出”复位。为下一周期执行X轴发送脉冲做准备。

当下一次，再进入本程序段时，由于“y加进位”仍为ON，故Y轴的累加不进行。而使“X步进”置位，进行X方向步进，同时使“y加进位”复位，为新一次的Y轴累加及相应操作做准备。

图4-73d为和利时LM程序。从图可知，当t1.Q ON的周期，将执行节8～15之间的指令。其他周期，则越过它，不执行其中指令。

图中“pxDa”（X行程大）ON，意味着X为基准轴。正如算法框图指出的，它先在节8，把“Ljiazh”（累加值）与“yD”（y终点）相加，其“和”赋值给累加值。然后，把累加值与“Ljia”（累加器）比较。而此“累加器”即为X轴的终点坐标值。

如果累加值小于累加器值，节9不执行，执行节10，则“yiJW”（y加进位）OFF，X轴输出脉冲（dx置位）。

如果大、等于“累加器”，节9不执行，则“y步进”置位（dx置位），输出脉冲。同时，把“yidy”（y已输出）置位。y已输出置位的目的是，在这个工作周期，不让X轴输出脉冲。但是临退出本程序段时，用y加进位ON，把y已输出复位。为下一周期执行X轴发送脉冲做准备。最后，把累加值被累加器减，其“差”赋值给累加值。

当下一次再进入本程序段时，由于y加进位仍为ON，故Y轴的累加不进行。而使X步进置位，进行X方向步进，同时在节11，使y加进位复位，为新一次的Y轴累加及相应操作做准备。

每执行一次本段程序，都会产生脉冲输出，不是使在X方向，就是在Y方向走一步。所以执行完本程序，都将使“已走步数”加1。

在节12，使“已走步数”加1。同时，进行“yizBUshu”（已走步数）与“xyZ”（设定总步数）比较。一旦前者大或等于后者，“stWF”（步进工作完成）ON（见图4-72节1），这可使stWK复位，步进工作停止。

本程序的节13为调用有限脉冲链输出功能块，规定输出脉冲数为1，x方向输出点为%QX1.0，y向输出点为%QX0.3。节14、15为了输出脉冲后dx、dy及时复位，确保每次调用只输出一个脉冲。

提示：在程序中，如不用“y已输出”信号进行控制，基准轴总是输出脉冲，而辅助轴累加值超过基准轴终点值时，也输出脉冲。运动轨迹将有时是走坐标轴的平行线，有时走斜线。速度将是不均匀的。

图4-74所示为PLC的终点及方向控制梯形图程序。

图4-74a为欧姆龙PLC程序。它主要是判断到了坐标终点了没有？如到，则置位“步进完成”。再看图4-74a可知，此信号将使“步进工作”停止。

此外，此程序还依选定的象限，对X、Y轴运动方向做了确定。图中只列出1、2象限的程序，3、4象限也类似。

图4-74b为西门子PLC程序。它也主要是判断到了坐标终点了没有？如到，则置位“步进完成”。再看图4-74b可知，此信号将使“步进工作”停止。

此外，此程序还依选定的象限，对X、Y轴运动方向做了确定。图中只列出1、2象限的程序，3、4象限也类似。

图4-74c为三菱PLC程序。它也主要是判断到了坐标终点了没有？如到，则置位“步进完成”。再看图4-74c可知，此信号将使“步进工作”停止。

此外，此程序还依选定的象限，对X、Y轴运动方向做了确定。图中只列出1、2象限的程序，3、4象限也类似。

图4-74d所示为和利时LM机程序。这里节17进行比较，节18、19、20及21是比较结果赋值。从图知，象限1，则dxFX（控制x方向）、dyFX（控制y方向）均置位。象限2，则dxFX（控制x方向）复位、dyFX（控制y方向）置位。象限3，则dxFX（控制x方向）复位、dyFX（控制y方向）复位。象限4，则dxFX（控制x方向）置位、dyFX（控制y方向）复位。它的输出点可任选。以上PLC程序讲的都是“X行程大”ON的情况，而“X行程大”OFF，与此类似。在本程序最后，使“已走步数”加1，为控制步进是否完成提供依据。

每执行一次本段程序，都会产生脉冲输出，不是使在X方向，就是在Y方向走一步。所以，执行完本程序，都将使“已走步数”加1。

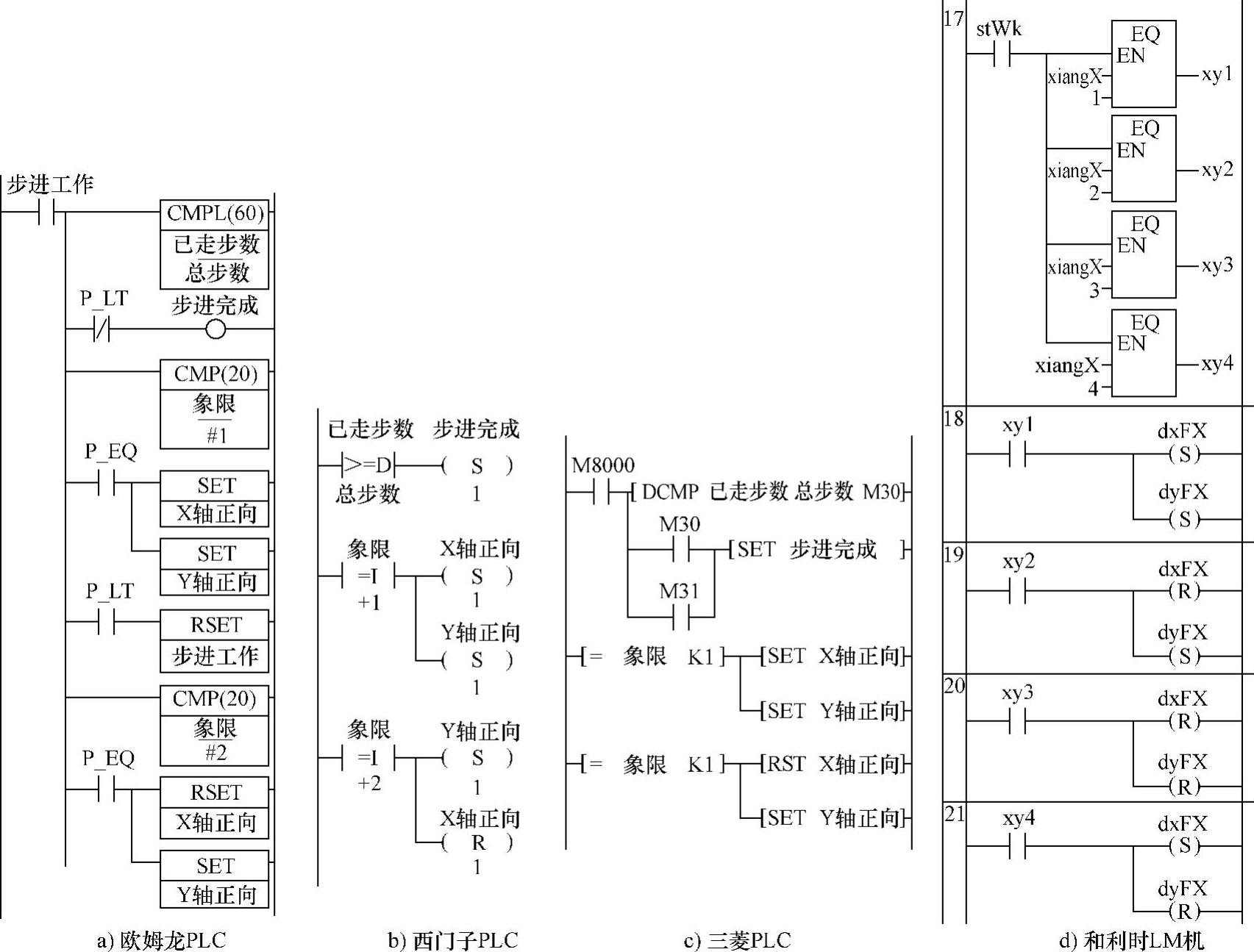
图4-74 终点及方向控制程序

提示：在这些程序中，如不用“y已走”信号进行控制，基准轴总是输出脉冲，而辅助轴累加值超过基准轴终点值时，也输出脉冲。运动轨迹将有时是走坐标轴的平行线，有时走斜线。速度将是不均匀的。

（2）圆弧插补法。

在两个坐标点间，如果要走曲线怎么办？把这曲线分成若干直线，用上述分几个直线段进行插补。这样，上述程序使用时及编程时，就要做分析：要分几段才能满足精度要求？每段的终点坐标是多少？然后，进行参数设定，并送入PLC。再运行上述程序，也可实行两点间的曲线运动。早期数控实现曲线运动，加工曲面就是这个办法。结果是使用的数据很多，编程（划分线段那样的编程）工作量很大。给数控的应用带来很大的不便。

在两个坐标点间，要走曲线第二个办法是用圆弧插补，有的还用其他二次曲线插补。这样插补比直线插补最大的优点是，达到相同的精度，所需的线段少，编程简单。但插补的运算复杂些。而后者是系统设计的问题，最终用户可不必考虑。

1）逐点比较法：同样圆弧插补，方法也较多。这里介绍的是较常用的逐点比较法。逐点比较法的基本思想是，走一步，比较一次。也可反过来说，比较一次，走一步。比较什么？看当前的位置是在圆弧内，还是圆弧外？如在圆内，则往外走。如在圆外，则往内走。为此，插补要分象限、按运动方向进行。如在第一象限，逆时针运动：只能是正Y及负X运动，而发送正Y向脉冲将是往外走；发送负X向脉冲将是往内走，如图4-75所示。其他各象限也都有相应的规律。

比较的关键还在于，怎么知道位置是在圆上、在圆内，还是在圆外？不难。如圆的半径为R。如在圆上，则其X的平方与Y的平方之“和”减去R的平方，即Δ，应为0。如在圆内，则其X的平方与Y的平方之“和”减去R的平方应小于0。如在圆外，则其X值的平方与Y值的平方和减去R的平方应大于0。

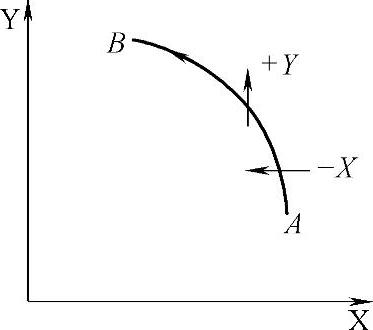
图4-75 一象限逆时针运动

只是这里都是平方计算，较难。但如只计算相对值，而不计算绝对值也不难。如已知在圆内，向某方向走了一步后还在不在圆内？这样的计算不难。

如现在圆上（在运动开始时，总是在圆上的），显然以下等式成立：

X²+Y²-R²=0

这时，如在正X向走一步，即X变为X+1，是否在圆内？可按下式计算：

Δ=（X+1）²+Y²-R²=X²+2X+1+Y²-（X²+Y²）=2X+1

即只计算2X+1，如为正，则在圆外。同理，如正Y走一步则计算2Y+1；如负X走一步则计算-2X+1；如正Y走一步则计算-2Y+1。而这些计算没有平方，只是乘2及加1，较简单。正是这样，逐点比较法用的很多。

图4-76所示为第一象限逆时针插补时的算法框图。

从图4-76可知，先是初始化，再是判断Δ＞0？若大，向负X走一步；若不大，则向正Y走一步。再计算Δ及X或Y值。判断是否到终点？到，退出。不到，返回判断，重复上述过程。图4-77所示为用此算法计算的简单运动实例。

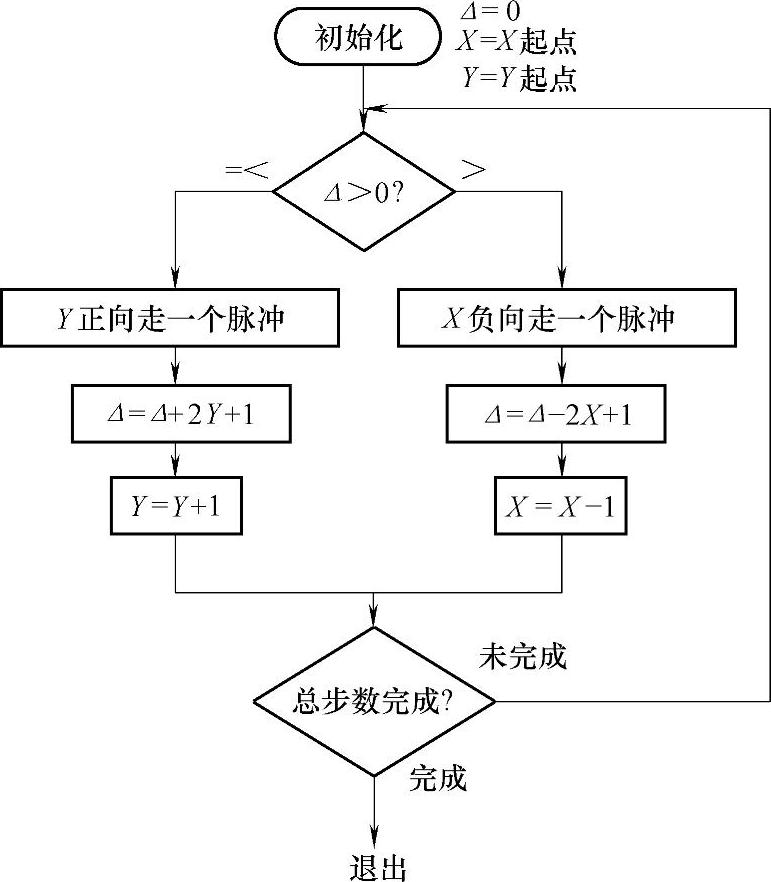
图4-76 第一象限逆时针插补的算法

从图4-77可知，它用第一象限逆时针插补的算法。X起点为5，终点为1。Y起点为1，终点为5。其计算与走步情况如下：

第1次时，Δ=0，走Y，计算Δ为3；

第2次时，Δ=3，走X，计算Δ为-6；

第3次时，Δ=-6，走Y，计算Δ为-1；

第4次时，Δ=-1，走Y，计算Δ为6；

第5次时，Δ=6，走X，计算Δ为-1；

第6次时，Δ=-1，走Y，计算Δ为8；

第7次时，Δ=8，走X，计算Δ为3；

第8次时，Δ=3，走X，计算Δ为0，到终点，停。

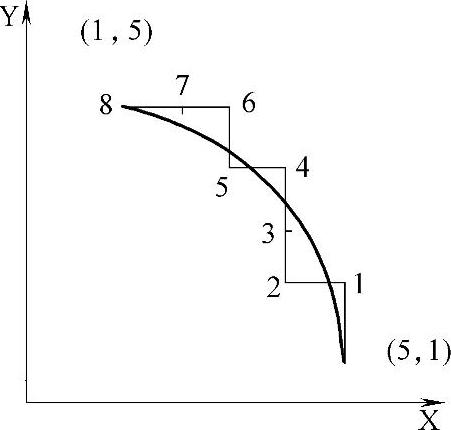
图4-77 法计算实例

提示：这里X起点、Y起点是以圆心为原点计算的。X终点、Y终点也应是如此。即这4个数是有相关关系的。

2）逐点比较法程序实现：相关PLC的圆弧插补初始化程序见图4-78。

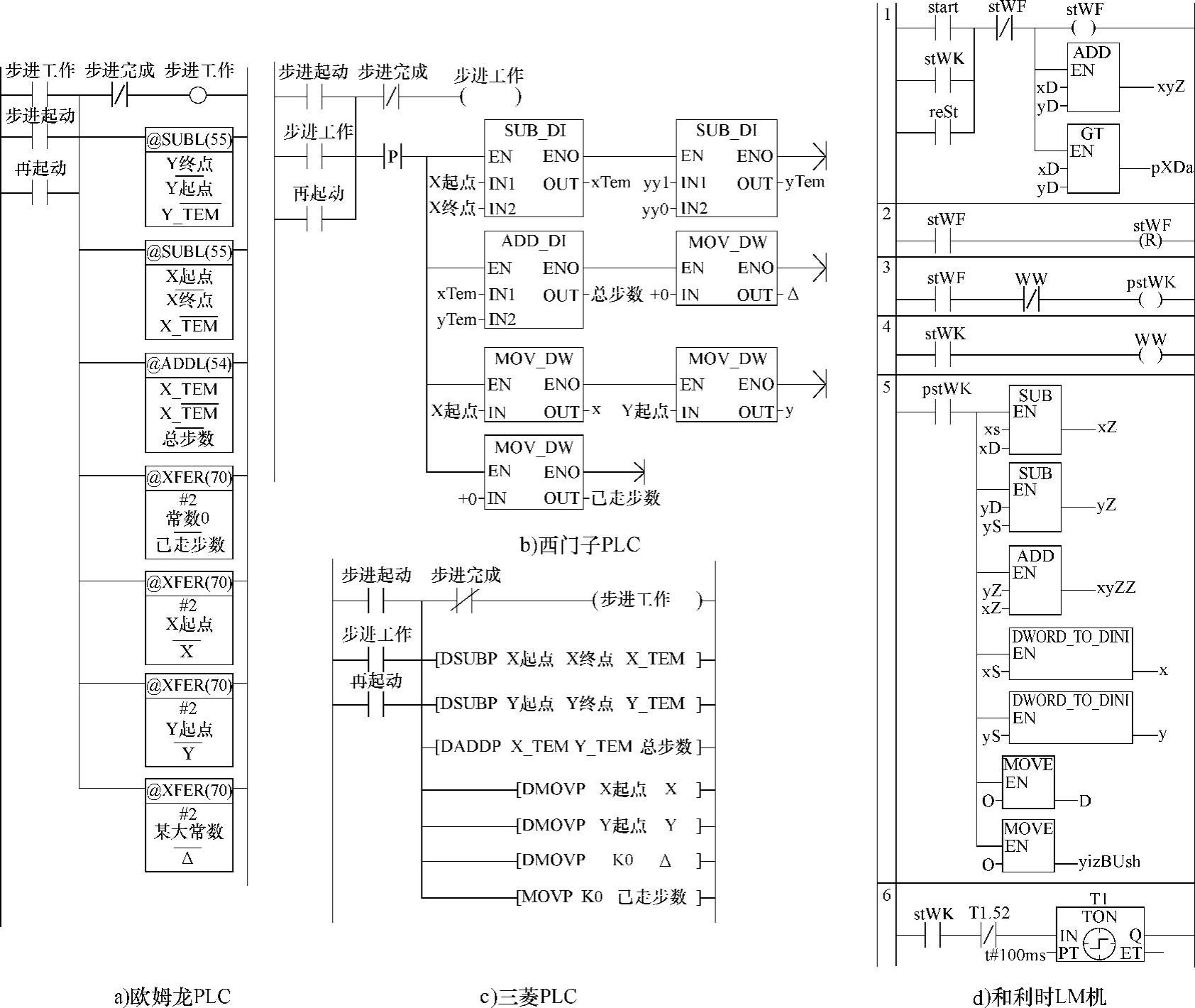
图4-78 圆弧插补初始化程序

从图4-78知，该程序先是起、保、停逻辑。“步进起动”ON，将使“步进工作”ON，并自保持。到“步进完成”ON，则“步进工作”OFF。这里并联“再起动”，为了选定新的程序后重起动的需要。

进入“步进工作”后，按算法进行初始化。计算总步数，把X起点赋值给X，Y起点赋值给Y，清零“已走步数”、并把0赋值给“Δ”。对图4-78a用“某大常数”赋值给，以作为Δ的基数。目的是使Δ，怎么加减，也不至于出现负值（因为CPM2A用的是双字BCD码运算，出现负数不好处理）。计算后的Δ则与“某大常数”比较，而不与0比较。效果是相同的。要不然，处理麻烦的事少多了。这也算是编程因地而为的一种技巧，不信不妨用传统的方法试试。

图4-79所示为相关PLC第1象限、逆时针插补时的处理程序。

图4-79a为欧姆龙PLC程序。从图知，它先是比较，把Δ与“某大常数”比较：小、等于时，发送正Y脉冲，并作算法要求的相应计算；大于时，发送负X脉冲，并作算法要求的相应计算。

图4-79b为西门子PLC程序。图4-79c为三菱PLC程序。它们是把Δ与常数0比较：小、等于时，发送正Y脉冲，并作算法要求的相应计算；大于时，发送负X脉冲，并作算法要求的相应计算。

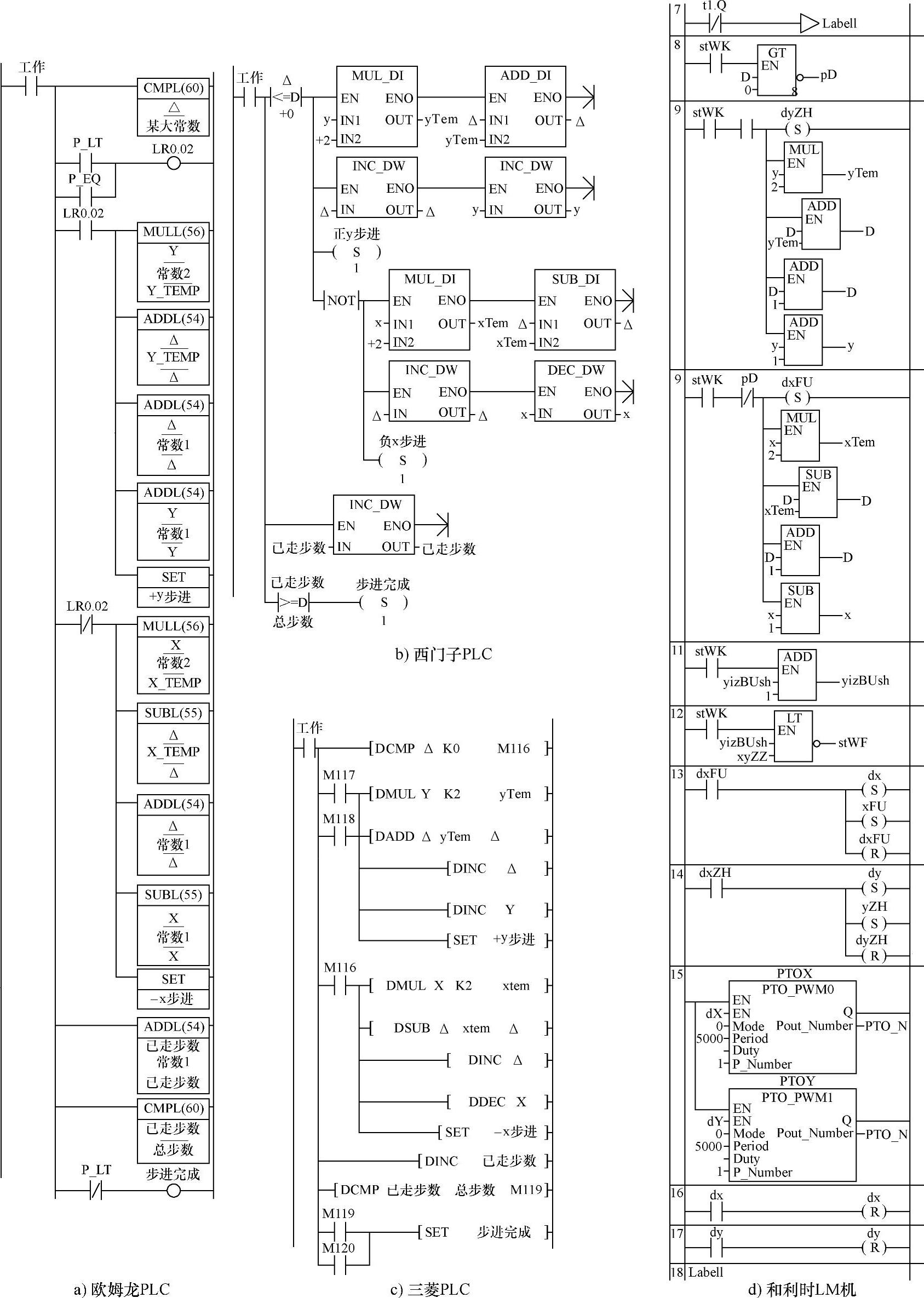
图4-79 第1象限、逆时针运动插补时圆弧插补运算程序

程序后面为“已走步数”加常数1，并与“总步数”比较，如相等或大于时，则“步进完成”ON。这将使“步进工作”OFF。

图4-79d为和利时LM机程序。从图可知，当t1.Q ON的周期，将执行节8～17之间的指令。其他周期，则越过它，不执行其中指令。图中节8为比较。只要“D”大等于0，则“pD”ON。这里“D”即为判断点位置的Δ值。如“pD”ON，则执行图4-79d中节9指令。进行Δ值计算，并使“dy”置位，以产生y向步进。如“pD”OFF，则执行图4-79d中节10指令。也进行Δ值计算，并使“dx”置位，以产生x向步进。

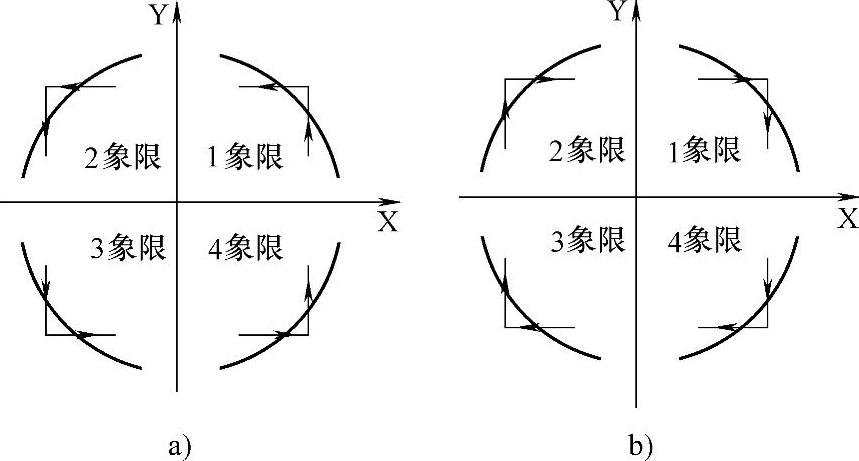
图4-80 各象限顺、逆时针运动趋势

图4-79d中节11为“yizbushu”（已走步数）加1。节12为判断“yizbushu”是否大等于“xyZZ”（应走的总步数）。如果前者已经等于后者，则“stWF”（步进工作完成）ON。进而，将使“stWK”OFF（见图4-79d节1）。

在节13、14，为置位脉冲输出及方向控制。并复位dyZH及dxFU，为新的步进做准备。

本程序的节15为调用有限脉冲链输出功能块，规定输出脉冲数为1，x方向输出点为%QX1.0，y向输出点为%QX0.3。节16、17为了输出脉冲后，dx、dy及时复位。为新的步进做准备。

图4-79程序不仅可用于第1象限、逆时针运动的插补控制，还可用于第3象限、顺时针运动。其他如图4-80所示，如第1象限、顺时针运动及第3象限、逆时针运动一样，在圆内，则走+X，在圆外，则走-Y；如第2象限、顺时针运动及第4象限、逆时针运动一样，在圆内，则走+Y，在圆外，则走+X；如第2象限、逆时针运动及第4象限、顺时针运动一样，在圆内，则走-X，在圆外，则走-Y。具体梯形图程序可在图4-79的基础上稍加修改即可。

（3）插补程序合成。

以上介绍的程序只能做一小段运动轨迹的插补。实际曲线复杂时，要做多段插补。多段中，可能有各个象限的小直线，还可能有各个象限、逆时针或顺时针的小圆弧。怎么把这样一段段运动连贯起来，就是插补程序合成要解决的问题。

图4-81所示是一种用程序控制实现的算法。

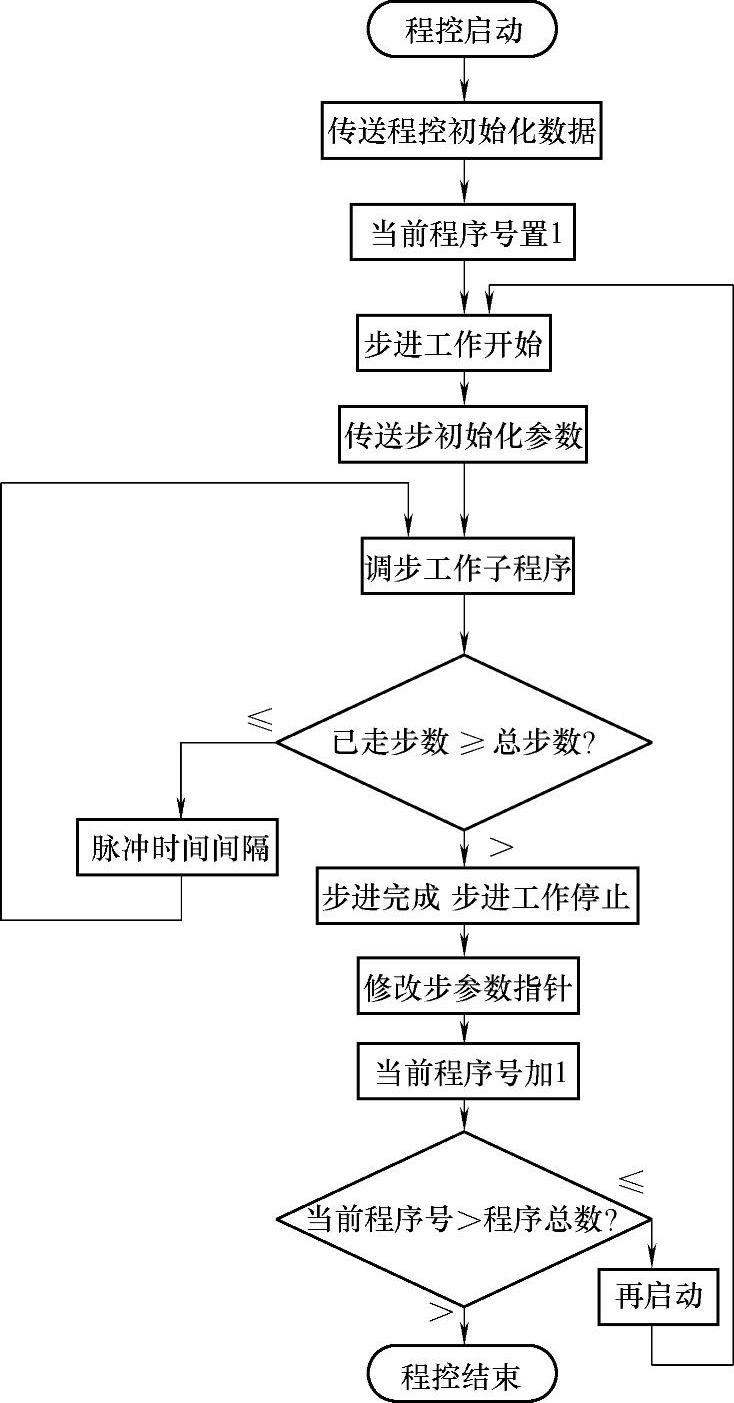
图4-81 程序控制算法

从图知，“程控启动”后，先传送“程控初始化数据”。这些数据有，程序总数（有多少上述小段程序？）、“当前程序号”置1、数据指针初始化（控制数据存放首地址）等。然后启动“步进工作”。“步进工作”开始时，先执行初始化程序，随后，调“步工作子程序”。每执行一次，都要判断步是否完成？如未完成，则相隔一个“脉冲时间间隔”，再调此子程序；如完成，则使“步进工作”OFF，并修改步参数指针、“当前程序号”加1，并比较“当前程序号”是否大于“程序总数”。如不大，则进入再启动，再使“步进工作”开始；如大，则已完成所有程序段的控制，将结束程控。

图4-82所示为相关PLC实现此算法的梯形图程序。

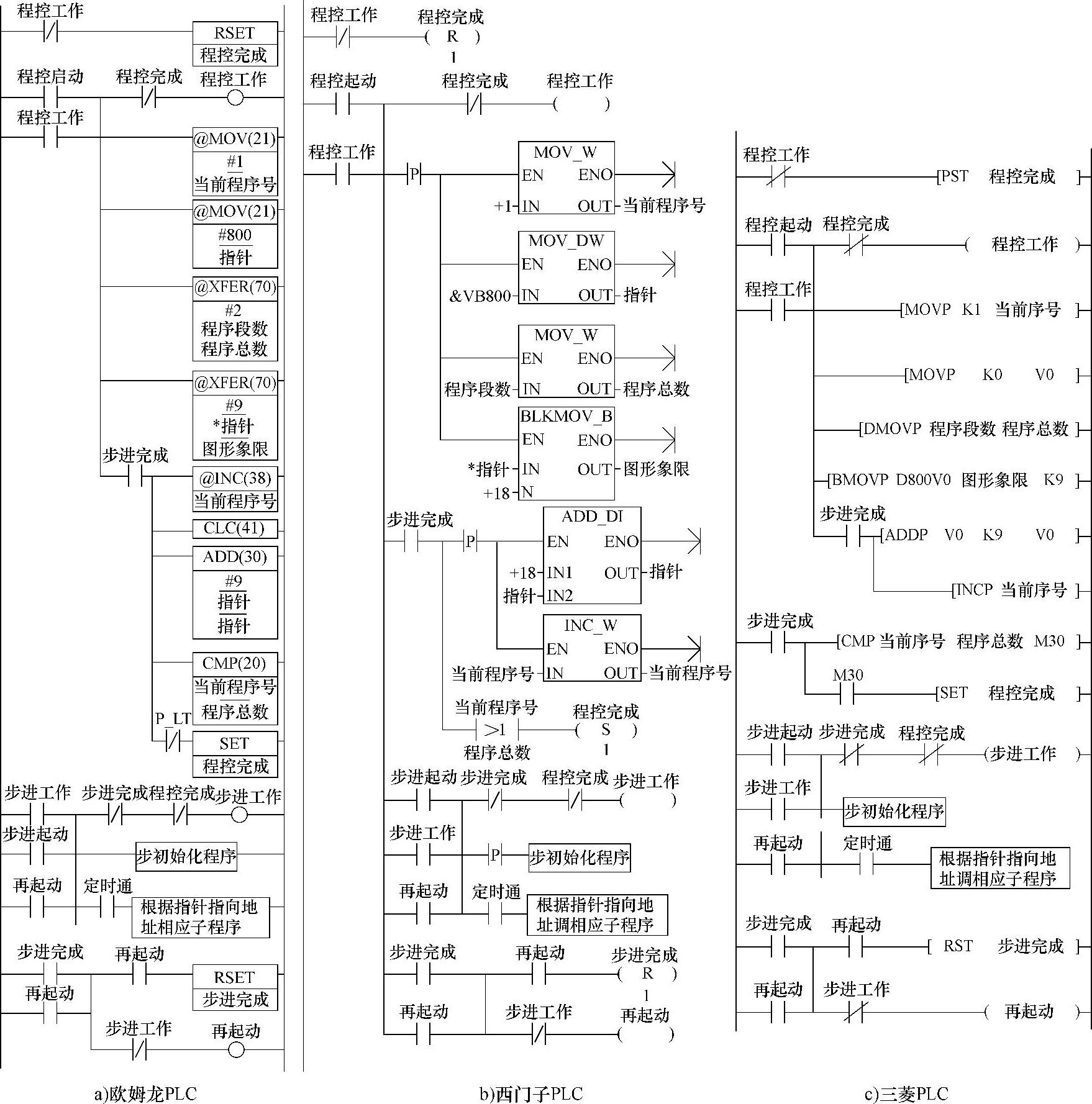
图4-82 相关PLC程序控制梯形图程序

图4-82a为欧姆龙PLC程序，当“程序工作”OFF时，“程序完成”复位。当“程序启动”ON，则当“程序工作”ON，并自保持。之后进行初始化：“当前程序号”置1，把800传“指针”（用作DM间接地址初值，即有关插补运算数据预先存储在DM800开始的地址中）、“程序段数”传给“程序总数”。同时，执行块传送指令，把DM 800开始的9个字数据，传送给“图形象限”等字或双字。这些数据有：“图形象限”、“X终点”、“Y终点”、“X始点”、“Y始点”。第1项占一个字，后4项每项占两字。这9个字是按插补要求，预先存于从800开始的DM数据区中的。有了这组数据，只要“步进工作”ON，即可定时调相应子程序，先进行步初始化（如图4-78、图4-72），后定时调相关程序（如图4-73、图4-79），即可进行相应控制。

当完成要求运动的总步数时，则“步进完成”置位。进而使“步进工作”OFF。同时，修改指针，使“当前程序号”加1，并“指针”加9，指向新的一组数据。而且当“步进工作”OFF后，从梯形图最后一个梯级知，它将使“再启动”ON，并自保持。这“再起动”ON将重新使“步进工作”ON，并自保持。同时使“步进完成”复位。“步进工作”再次ON，先也是步初始化，可得到新的一组“图形象限”等控制数据。进而，又可定时调相应控制程序，进一步进行相应控制了。

当一段段插补程序运行结束，即“当前程序号”大于“程序总数”时，“程控完成”ON，它将使“程控工作”、“步进工作”OFF，使整个程序结束。

图4-82b为西门子PLC程序。

从图知，当“程序工作”OFF时，“程序完成”复位。当“程序起动”ON，则当“程序工作”ON，并自保持。之后进行初始化：“当前程序号”置1，把VB800的地址赋值给“指针”（把有关插补运算数据预先存储在VB800开始的地址中）、“程序段数”传给“程序总数”。同时，执行块传送指令，把VB 800（指针指向的首地址）开始的18个字节数据，传送给“图形象限”等字或双字。这些数据有：“图形象限”、“X终点”、“Y终点”、“X始点”、“Y始点”。第1项占一2个字节，后4项每项占4字节。这18个字节是按插补要求，预先存于从VB800开始的V数据区中的。有了这组数据，只要“步进工作”ON，即可定时调相应子程序，先进行步初始化（如图4-78、图4-72），后定时调相关程序（如图4-73、图4-79），即可进行相应控制。

当完成要求运动的总步数时，则“步进完成”置位。进而使“步进工作”OFF。同时，修改指针，使“当前程序号”加1，并“指针”加18，指向新的一组数据。而且当“步进工作”OFF后，从梯形图最后一个梯级知，它将使“再起动”ON，并自保持。这“再起动”ON将重新使“步进工作”ON，并自保持。同时使“步进完成”复位。“步进工作”再次ON，先也是步初始化，可得到新的一组“图形象限”等控制数据。进而，又可定时调相应控制程序，进一步进行相应控制了。

当一段段插补程序运行结束，即“当前程序号”大于“程序总数”时，“程控完成”ON，它将使“程控工作”、“步进工作”OFF，使整个程序结束。(www.daowen.com)

图4-82c为三菱PLC程序。

从图知，当“程序工作”OFF时，“程序完成”复位。当“程序启动”ON，则当“程序工作”ON，并自保持。之后进行初始化：“当前程序号”置1，把变址器V0置0、“程序段数”传给“程序总数”。同时，执行块传送指令，指定把D800V0（800加变址器V0的值作为D区的首地址）地址开始的9个字传送给“图形象限”等字或双字。这些数据有：“图形象限”、“X终点”、“Y终点”、“X始点”、“Y始点”。第1项占一2个字节，后4项每项占4字节。这18个字节是按插补要求，预先存于从D800开始的D数据区中的。有了这组数据，只要“步进工作”ON，即可定时调相应子程序，先进行步初始化（如图4-78、图4-72），后定时调相关程序（如图4-73、图4-79），即可进行相应控制。

当完成要求运动的总步数时，则“步进完成”置位。进而使“步进工作”OFF。同时，修改指针，使“当前程序号”加1，并V0的值加9，指向新的一组数据。而且，当“步进工作”OFF后，从梯形图最后一个梯级知，它将使“再起动”ON，并自保持。这“再起动”ON将重新使“步进工作”ON，并自保持。同时使“步进完成”复位。“步进工作”再次ON，先也是步初始化，可得到新的一组“图形象限”等控制数据。进而，又可定时调相应控制程序，进一步进行相应控制了。

当一段段插补程序运行结束，即“当前程序号”大于“程序总数”时，“程控完成”ON，它将使“程控工作”、“步进工作”OFF，使整个程序结束。

图4-83所示是和利时LM机程序。首先，要声明的一个“nc1”结构。具体如下：

其次，还要声明一个“nc1”结构变量的数组。具体如下：

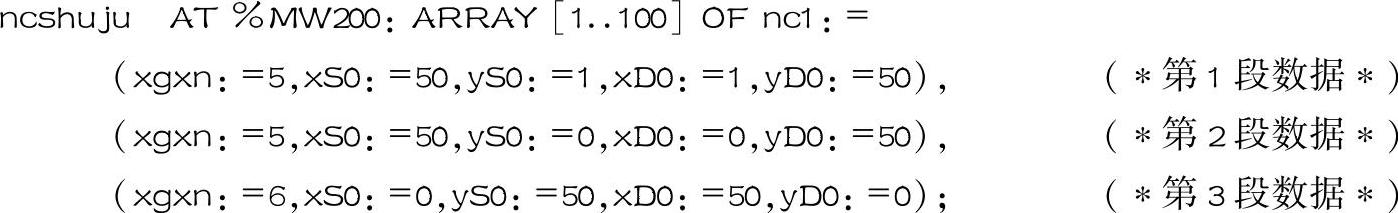
这里，只设定3段数据。如果需要，可设多达100段。100段，共900个字。指定与地址%MW200～%MW1099关联。由于和利时LM机M存储可多达6K字，所以，如果需要，此数组还可以扩大。与M区地址关联的目的是，可利用上位机设定与下载数组数据，比在PLC程序中设定要方便些。

图4-83中节1为步进起动程序。当所有插补程序完成“chkwch”（程控完成）ON。其常闭触点把“stWK”（步进工作）复位、OFF。

节2为了“chkwch”及“indx”索引及时复位，以及为下一次启用步进工作创造条件。

节3、4为了“stWK”再起动。当步进完成，“stWF”ON，先是使“stWK”OFF，进而使“rest”（再起动）ON，并自保持。接着，是节3使“stWF”复位。之后在节1，使“stWK”ON，并自保持。最后，在节4，又使“rest”复位。为新的再起动做好准备。

这初始化程序则多是微分执行的。节5、6是为了产生微分信号“pstWK”。

节7就是用微分信号执行的3个指令。目的是在“stWK”ON的第1个周期，使数组索引“indx”加1，圆插补运算的Δ值，及即“D”“yizBUsh（已走步数）”清零。

节8为控制索引“indx”及控制“yizBUsh（已走步数）”，超出时，将使“chkwch”（程控完成）ON，或“stWF”（步进完成）ON，以控制程控结束，或进行再起动。此外，还进行“nc1”结构数组的“xgxn”（插补类型）与0比较，若为0则“nwork”置位。从节10可知，只要“stWK”ON，步进工作将使“indx”不断增1，直到“indx”大于等于100，而使“chkwch”（程控完成）ON，控制程控结束。

节9为根据“nc1”结构数组的“xgxn”（插补类型）与1、2、3…等比较，将使“Line1”、“yuan1”等中的一个置位。根据不同的置位，以调用不同的程序块，进行插补运算。这些插补总共有12种。即直线1、2、3、4象限。逆圆1、2、3、4个象限。顺圆1、2、3、4个象限。

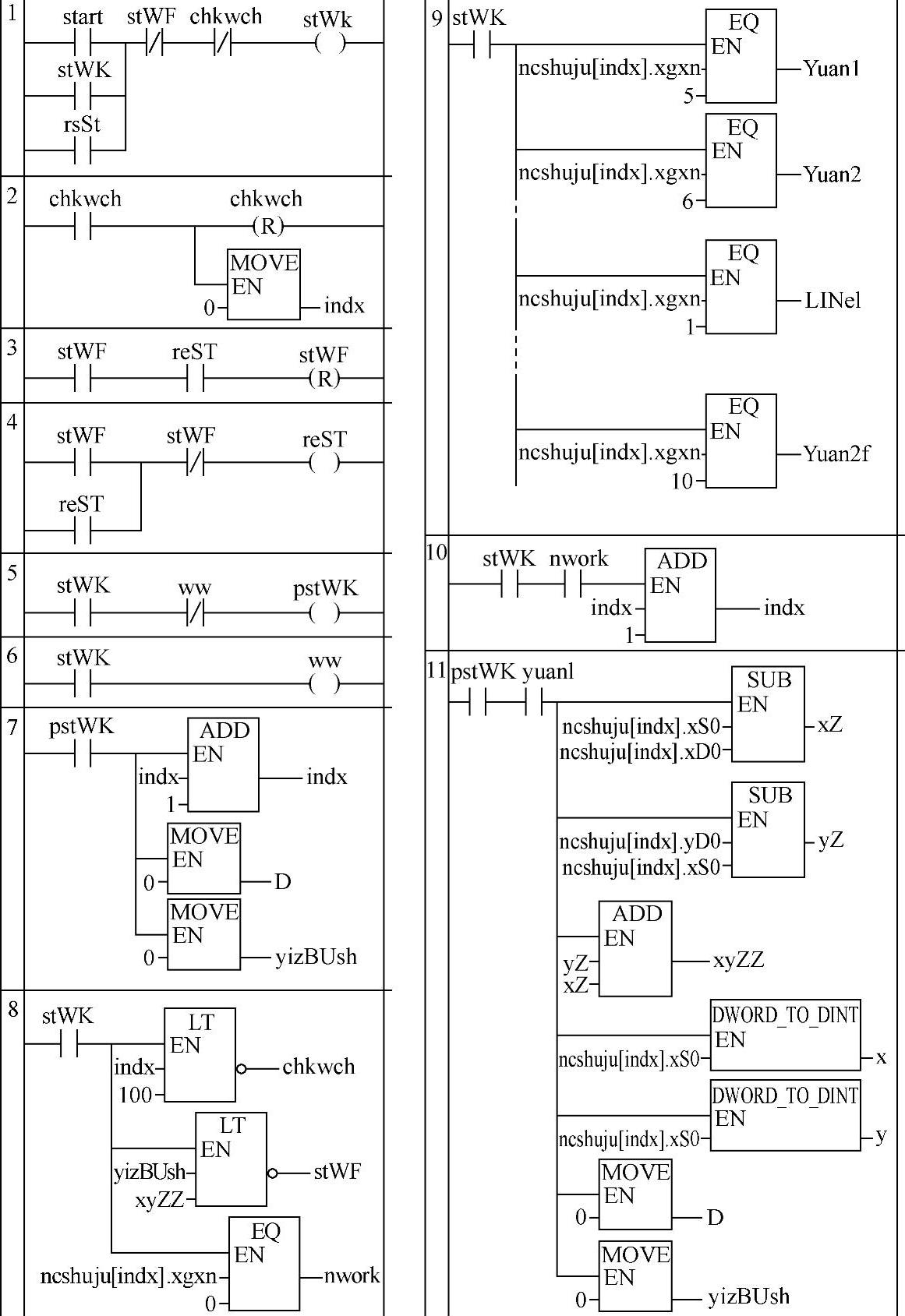
图4-83 和利时LM机程序控制梯形图程序

节11为逆圆1象限插补的初始化（yuan1 ON）。计算步总数，对x、y赋值等。与图4-77程序相同。只是这里用的设定的数组的数据。

以下还有调用程序块。这里省略。

提示：和利时LM机可以用于结构、数组设定程控参数是很方便的，是别的PLC难以这么处理的。这也可以看出PLC变量类型多的好处。

2.直接目标跟踪控制

上述插补算法是早期数控控制机常用的算法。随着计算机工作速度的提高及计算能力的增强，如果对象的运动轨迹有确定表达式，也可直接目标追踪实现轨迹控制，而不必作分段插补。

（1）目标追踪算法。

1）根据对象运动轨迹表达式，选定一个合适的参变量，把表达式转换为参变量方程。要确保参变量的单值变化能覆盖整个运动轨迹。

2）使参变量微小增（或减）变化（变化范围应覆盖整个运动轨迹），逐一计算目标值X、Y的变化。

3）判断目标值X或Y是否出现单位值增、减的情况，如出现，输出脉冲，使控制对象在X或Y坐标方向作增或减1运动。

4）判断是否到达终点，否，则继续使参变量微小增减，重复上述2、3过程；是，控制结束。

（2）目标追踪算法实例。

以下以图4-84所示的螺旋线轨迹为例，介绍此算法设计及其程序实现。螺旋线用参变量θ表示它的轨迹。

如图所示，其中ρ与k、θ及X、Y与θ、ρ间的关系式如下：

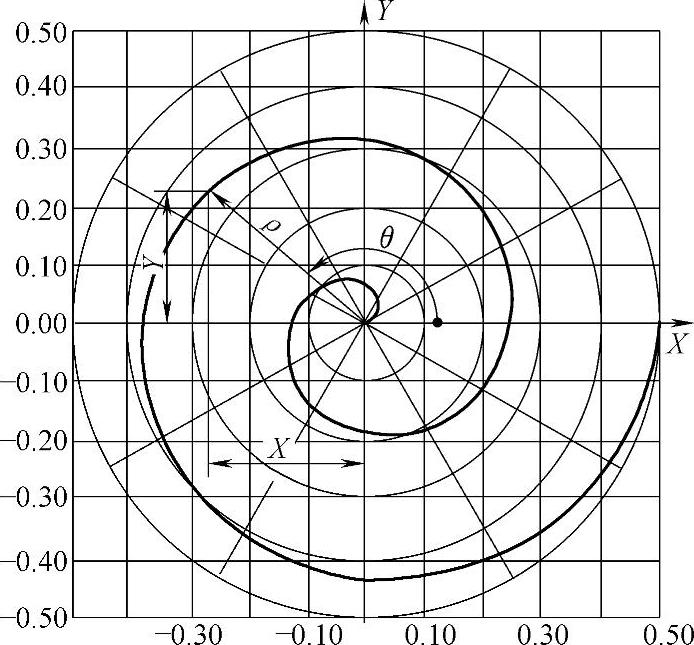
图4-84 螺旋曲线图形

ρ=k·θ

X=ρ·cosθ

Y=ρ·sinθ

θ从0～4π，将覆盖整个轨迹。该图表示了在X、Y坐标上“步进”，完成这个运动轨迹的控制情景。图4-85所示为这个算法图解。

从图知：

1）初始化：使目标坐标值X、Y、实际坐标值X0、Y0及参变数θ均置0，同时，把“某较小数”赋值给Δθ及设定螺旋圈数n及系数k。

2）计算：按图示公式，计算目标值X、Y。这里“某较小数”要小到加此值后，最多只能使X或Y的增量为1。

3）比较：做4个比较，如都为“否”，则使θ加Δθ。否则如X与X0比较有一个“Y（是）”，则修改实际坐标值，做相应步进。等待脉冲时间间隔后再对Y与Y0进行比较。后者比较若“Y（是）”，则也修改实际坐标值，做相应步进。等待脉冲时间间隔后进入下一步。

4）判断：判断是否达到终点，即Y0=0及X0=2π∗n∗k是否成立。是退出控制，不是又使θ加Δθ，回到2）。

可知，按图示算法，将用一段段平行于X、Y坐标的小短线，近似地走出螺旋线来。这个近似最大误差将不大于一个步进的行程，即脉冲当量。

（3）目标追踪算法梯形图程序实现。

图4-86所示为实现上述算法的相关PLC梯形图程序。当未达到终点时，每隔一个脉冲间隔时间，将调用一次本程序。但在此没有列出工作控制及终点判断等有关程序。

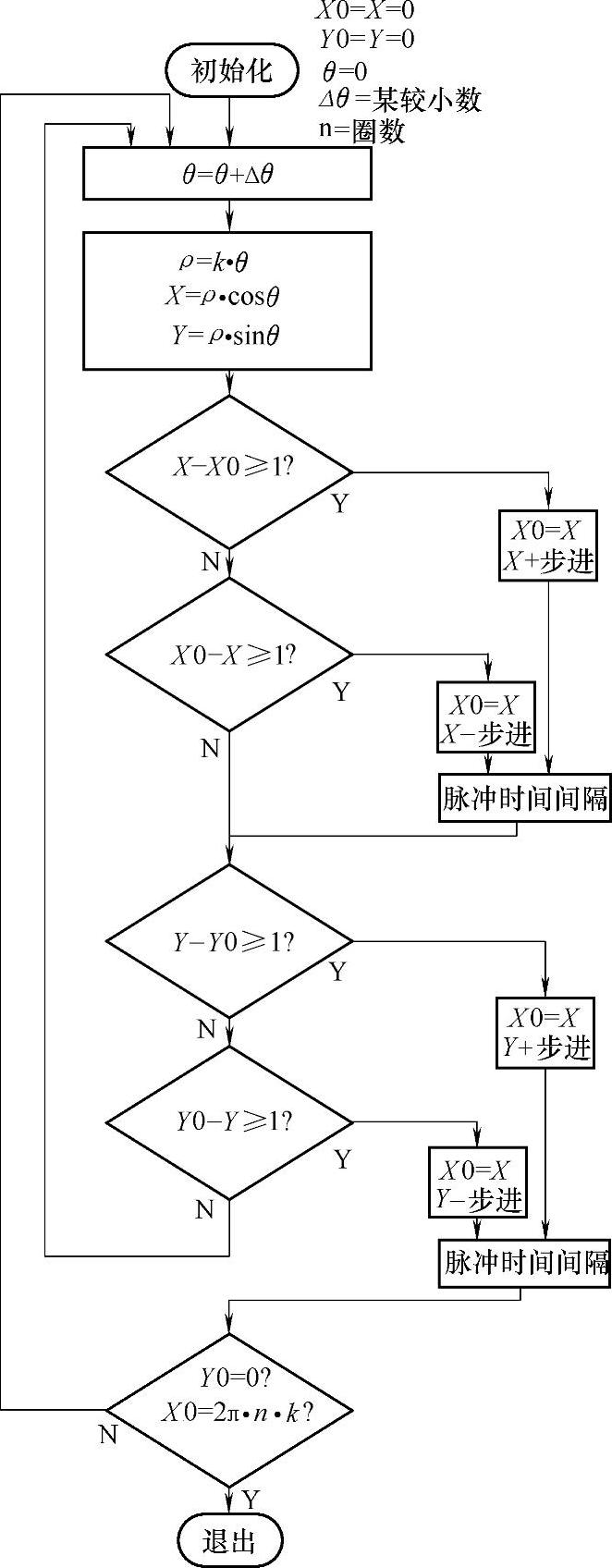
图4-85 螺旋线轨迹直接目标追踪控制算法

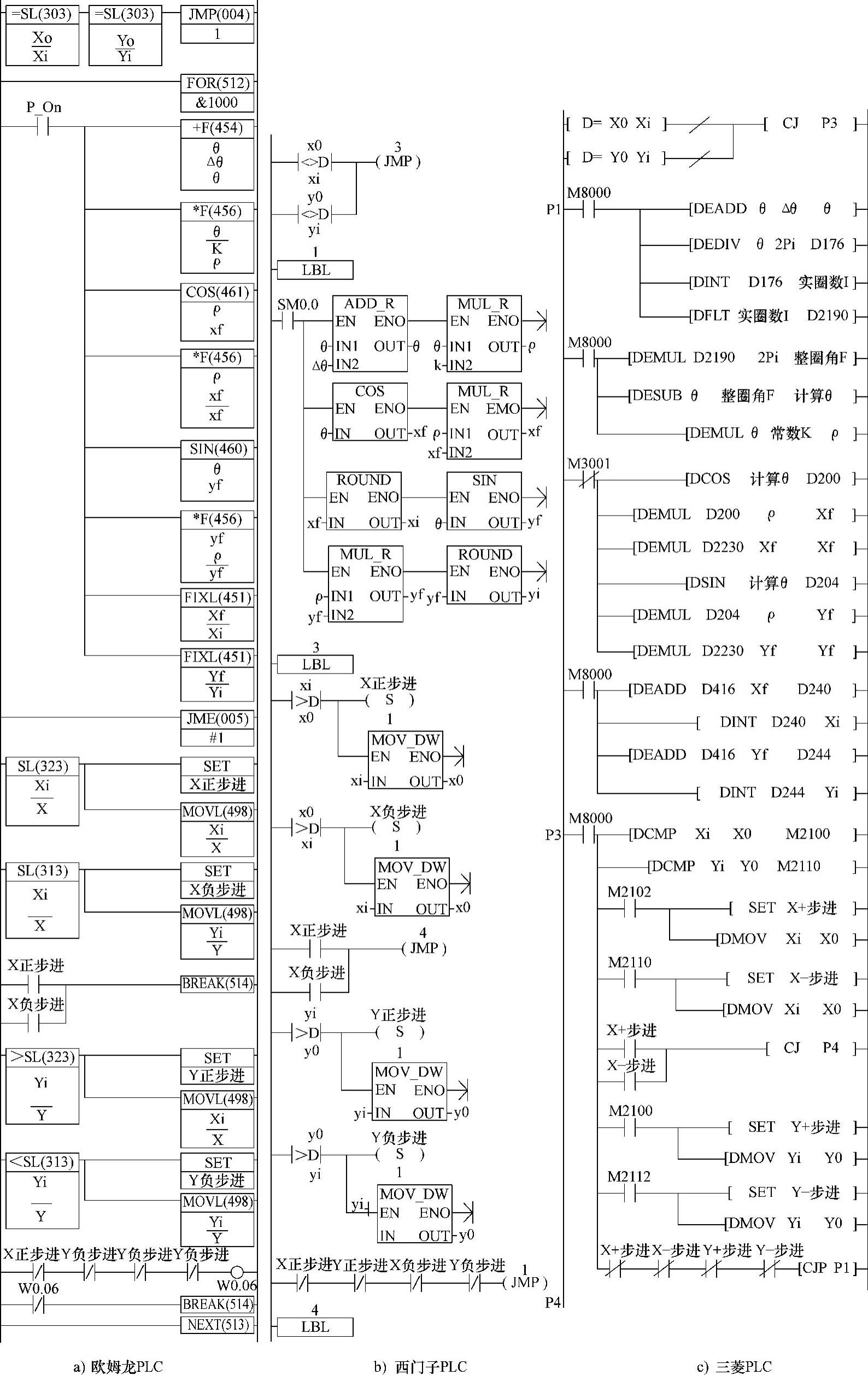
图4-86 螺旋线运动轨迹控制梯形图程序

图4-86a为欧姆龙PLC程序。从图知，进入本程序时，先比较Xi与X0、Yi与Y0是否相等。有任一组不相等时，则JMP 1与JME之间的指令将跳过，直接进入进一步比较，确定是否设置“步进”。如满足一个设置“步进”条件，则输出脉冲，并随后传送数据，使不等的变成相等。这样，下一次再进入时，此不相等的条件将不存在了。

其后是在FOR、NEXT间的指令，最多可重复执行100次。其任务是使θ增Δθ，按螺旋线的参数方程，进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。接着进入比较Xi与X0、Yi与Y0是否相等。由于Δθ是“某较小数”。要求这个数要小到带给θ变化而引起的Xf、Yf的增减数不能大于1，所以，这里如不相等，也仅相差1，可确保每次步进仅一个脉冲当量。Xi与X0、Yi与Y0比较结果有4种情况：

1）Xi与X0及Yi与Y0均相等，则继续重复执行，又使θ再增Δθ，及进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。进而又回到这里比较。显然，由于螺旋线的X、Y坐标总是要随θ的增加而变化的，一般在100次内总能出现不等的情况。

2）Xi与X0相等，所以，不会出现步进。而Yi与Y0不等，将使Y步进。并把Yi传送给Y0。同时执行BREAK指令，跳出重复执行，跳出本程序。

3）Xi与X0不等，而Yi与Y0相等，将使X步进。并把Xi传送给X0，跳出重复执行，跳出本程序。

4）Xi与X0、Yi与Y0均不等，将先使X步进。并把Xi传送给X0，跳出重复执行，跳出本程序。但下一次执行本程序时，由于Yi与Y0不等，将直接进入这个比较使Y步进。这样处理的目的是可做到每次“步进”只能在一个坐标上进行，可得到均匀的运动速度。

图4-86b为西门子PLC程序。从图知，进入本程序时，先比较Xi与X0、Yi与Y0是否相等。有任一组不相等时，则跳转到标号3处，以进一步比较，确定是否设置“步进”。如满足一个设置“步进”条件，则输出脉冲，并随后传送数据，使不等的变成相等。这样，下一次再进入时，此不相等的条件将不存在了。

其后是使θ增Δθ。接着按螺旋线的参数方程，进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。

接着进入已提到的标号3程序，比较Xi与X0、Yi与Y0是否相等。由于Δθ是“某较小数”。要求这个数要小到带给θ变化而引起的Xf、Yf的增减数不能大于1，所以，这里如不相等，也仅相差1，可确保每次步进仅一个脉冲当量。Xi与X0、Yi与Y0比较结果有4种情况：

1）Xi与X0及Yi与Y0均相等，那将跳转到标号1，又使θ再增Δθ，及进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。进而又回到这里比较。显然，由于螺旋线的X、Y坐标总是要随θ的增加而变化的，所以，这个过程不会出现“死循环”。

2）Xi与X0相等，所以不会出现步进。而Yi与Y0不等，而Xi与X0相等。这将使Y步进。并把Yi传送给Y0。

3）Xi与X0不等，而Yi与Y0相等，将使X步进。并把Xi传送给X0，同时跳转到标号4，退出本程序。

4）Xi与X0、Yi与Y0均不等，将先使X步进。并把Xi传送给X0，同时跳转到标号4，退出本程序。但下一次执行本程序时，由于Yi与Y0不等，将直接进入这个比较使Y步进。这样处理的目的是可做到，每次“步进”只能在一个坐标上进行，可得到均匀的运动速度。

图4-86c为三菱PLC程序。从图知，进入本程序时，也是先比较Xi与X0、Yi与Y0是否相等。有任一组不相等时，则跳转到标号P3处，以进一步比较，确定是否设置“步进”。如满足一个设置“步进”条件，则输出脉冲，并随后传送数据，使不等的变成相等。这样，下一次再进入时，此不相等的条件将不存在了。

其后是使θ增Δθ。接着按螺旋线的参数方程，进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。只是由于FX2N机三角函数的θ值，只在小于或等于2π时有效，大于时按2π处理。为此，当螺旋圈数大于1，即θ大于2π时，要计算“计算θ”，它是θ减2π后的值，用这个“计算θ”再作三角函数的自变量。再加上在浮点数与整形数之间类型还需转换，所以，它的这个计算程序比S7-200的程序稍麻烦一些。

接着进入已提到的标号P3处，比较Xi与X0、Yi与Y0是否相等。由于Δθ是“某较小数”。要求这个数要小到带给θ变化而引起的Xf、Yf的增减数不能大于1，所以，这里如不相等，也仅相差1，可确保每次步进仅一个脉冲当量。Xi与X0、Yi与Y0比较结果有4种情况：

1）Xi与X0及Yi与Y0均相等，那将跳转到标号1，又使θ再增Δθ，及进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。进而又回到这里比较。显然，由于螺旋线的X、Y坐标总是要随θ的增加而变化的，所以，这个过程不会出现“死循环”。

2）Yi与Y0不等，而Xi与X0相等。这将使Y步进。并把Yi传送给Y0。而Xi与X0相等，所以，不会出现步进。

3）Xi与X0不等，而Yi与Y0相等，将使X步进。并把Xi传送给X0，同时跳转到标号4，退出本程序。

4）Xi与X0、Yi与Y0均不等，将先使X步进。并把Xi传送给X0，同时跳转到标号4，退出本程序。但下一次执行本程序时，由于Yi与Y0不等，将直接进入这个比较使Y步进。这样处理的目的是可做到每次“步进”只能在一个坐标上进行，可得到均匀的运动速度。

图4-87所示为和利时LM机程序。图中节1、2为启动初始化程序，目的进行控制参数赋值或清0。

节3为启动程序。当“start”ON，将使“WK”ON，并自保持。启动后，将一直进行x值与R0比较。一旦前者等于后者，将使“WKF”ON。进而使“WK”OFF，停止工作。

当“WK”ON时，节4启动定时功能块T1。按图设定，它的输出端每隔5ms ON一个扫描周期。正是用它控制脉冲输出的节奏，即频率。

节5为跳转到节14。但T1输出ON的周期不跳转，将执行节6～14间的指令。

节6为x与x0及y与y0比较。有任一组不相等时，将使节7的输出a4 ON，将使节8的运算不进行。

节8执行目标值运算。其任务是使A增dA，按螺旋线的参数方程，进行RR、X及Y浮点计算，并取整。在取整前，X、Y还可先加0.5，以实现四舍五入，以克服“TRUNC”指令仅仅为“截短”的不足。

节9进行X与X0、Y与Y0比较，结果有4种情况：

1）X与X0及Y与Y0均相等，则从节10知，程序将跳转到节8，继续使A再增dA，及进行RR、X及Y浮点计算。然后对X、Y取整。进而又回到节9比较。显然，由于螺旋线的X、Y坐标总是要随A的增加而变化的，一般在若干次后，总能出现不等的情况。

2）X与X0不等，而Y与Y0相等，将使X步进（在图中没有示出）。并把X传送给X0，接着跳出本程序。

3）X与X0相等，所以不会出现步进。而Y与Y0不等，将使Y步进（在图中没有示出）。并把Y传送给Y0。

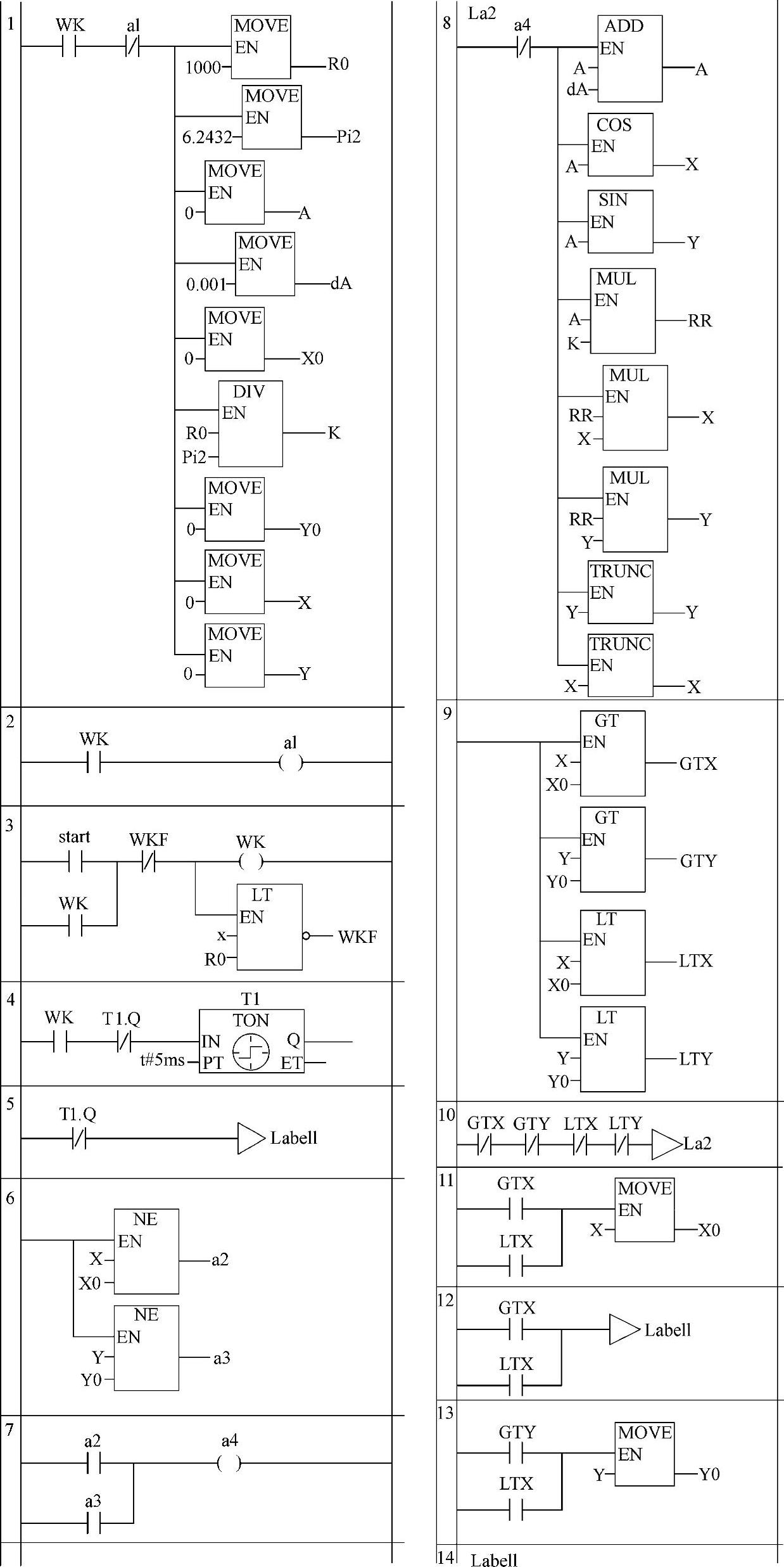
图4-87 和利时LM机螺旋线运动轨迹控制梯形图程序

4）X与X0、Y与Y0均不等，将先使X步进。并把X传送给X0，跳出重复执行，跳出本程序段。但下一次执行本程序段时，由于Y与Y0不等，将直接进入这个比较使Y步进。这样处理的目的是，可做到每次“步进”只能在一个坐标上进行，可得到均匀的运动速度。

以上讨论的螺旋线是逆时针，从第1象限开始的。还可以为顺时针，或者从其他象限开始。这些控制都可以在本程序的基础上稍作修改，也都可以实现。

此外，有关步进输出的处理，与上述插补程序相同。所以这里没有示出，也不再重复说明。

协调运动控制，除了二维的运动控制，理论上讲也可以进行多维控制。只是程序设计要困难些。而且控制速度与控制规模的矛盾将更加突出。所以较高性能的运动控制还是使用专用的硬件模块为好。

提示：直接目标跟踪控制的算法，不仅可以用于本例的螺旋线轨迹控制，其他曲线，以至于多维曲线轨迹控制，只要它的轨迹可用参数方程单值表达，也都可以用此小本算法实现。只是要求PLC要有很高的运算速度。

（4）目标追踪算法ST语言功能块实现。

ST语言擅长于执行运算程序，所以用其设计本算法的程序实现是较为简单的。以下为欧姆龙PLC用它的功能块程序。

使用的变量声明有输入、输出及内部变量。

图4-88所示为欧姆龙PLC功能块调用梯形程序。

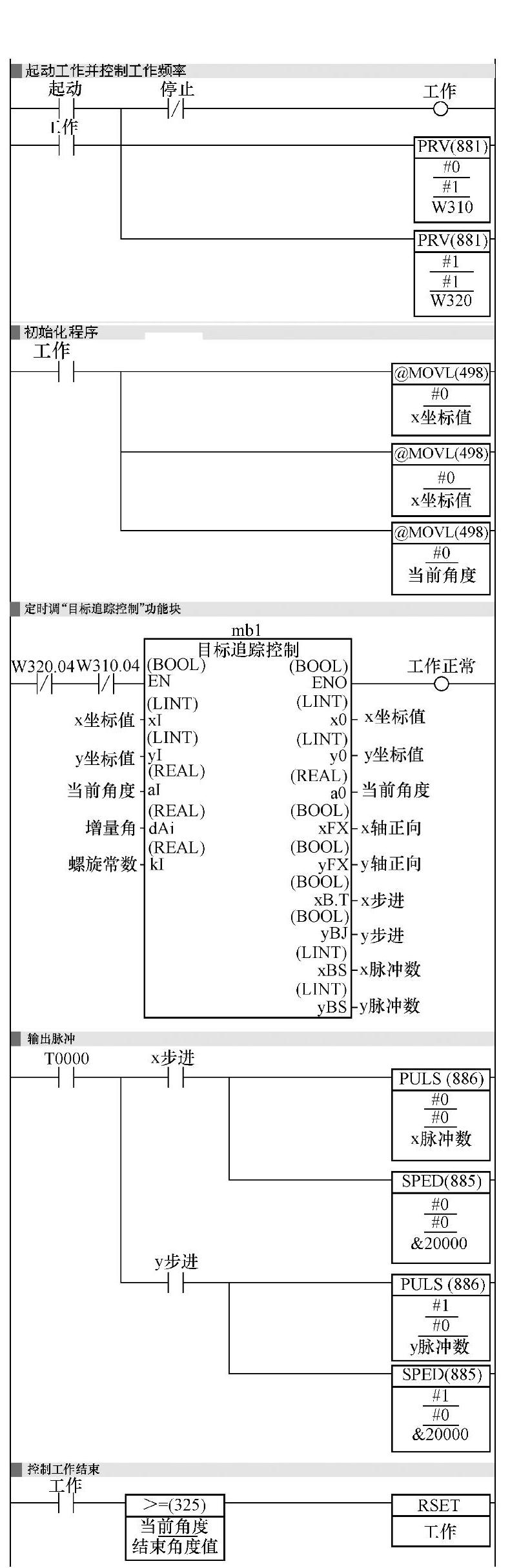
图4-88 欧姆龙PLC功能块调用梯形图程序

从图知。它有4梯形条。每梯形条的功能见注解。具体说明略。

3.相对值数据列表运动控制

除了插补、目标跟踪，还可用相对与绝对数表，即数据列表进行运动控制。

（1）相对数据列表算法要点。把运动轨迹按单位脉冲分步，依次计算每步的X、Y（取决于坐标数）增量值，并列写成数表，存储于PLC的数据存储区（D区）中。PLC程序就是按数表要求，向各个坐标输出脉冲，进而实现运动的协调运动。

这对既不便进行直线或圆弧插补，又没有合适的解析式子可用的运动轨迹控制是唯一可实现的算法。事实上，早期如航空发动机涡轮叶片这样的型面的数控加工也就是这么处理的。

（2）相对数据列表算法实现程序。为了节省内存，该程序用的数表为每个字的4个数位，分别存一组数据，即x及y两坐标的增1或减1值。其含义是，数位0：字的0位1，表示x增1，1位1，表示x减1；字的2位1，表示y增1，3位1，表示y减1；数位1：字的4位1，表示x增1，5位1，表示x减1；字的6位1，表示y增1，7位1，表示y减1。数位2、3依次类推。所有数据存储在D0开始的字中。CP1H机D区有32K字，可存储128K组数据。每组数据若生成一个脉冲，而脉冲当量若为0.01mm，则可控制1280mm的行程。这样行程与分辨率对一般机床是足够用的。图4-89所示为这样增量值数表使用程序。

该图有16个梯形条。条1为起动与初始化。起动使W0.10 ON后，把D0的地址赋值给索引寄存器IR0，并使W98、99（用于计数）、W80、81（用于数位移位处理）清零。同时，调PRV指令，读取脉冲输出口0、1的状态。如果已起动并两个输出口已完成脉冲输出，将按“ON”条件执行梯形条3～16间指令。

梯形条14用于计数及使数位变化。当每次脉冲输出完成，都使W98、99加1，同时把W98、99被4整除。除后，其商存于W79、80，余数存于W81、82。显然，随着W98、99值的变化，W81的值将在0～3之间变化。这样，W98、99可用于结束控制。而W81.00与W81.01的变化，即可用于控制4个数位的使用。

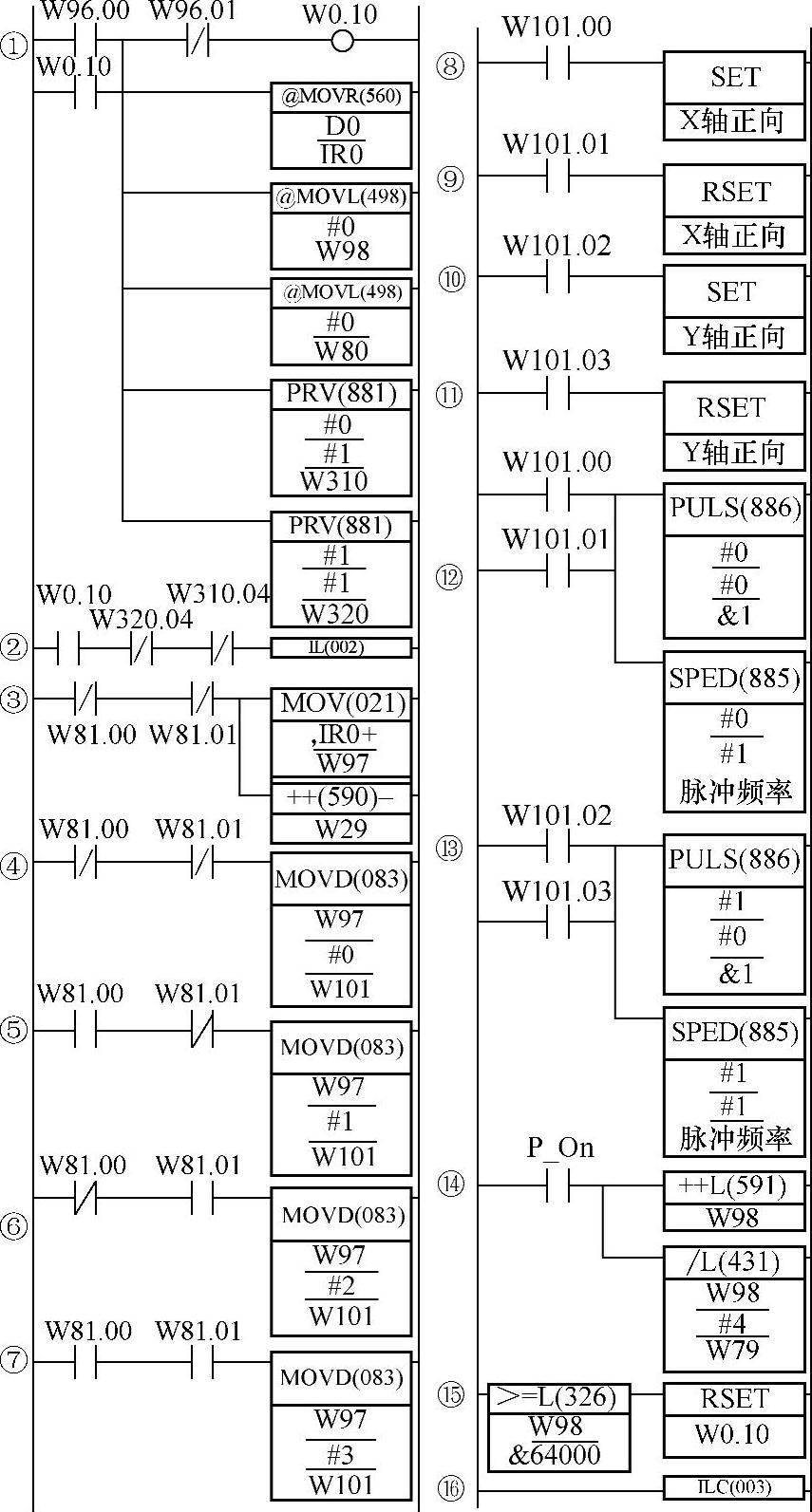
图4-89 增量值数表运动控制程序

梯形条3。由于开始时W81为0，即W81.00与W81.01常闭触点均ON，故可把IR0指向的地址字（开始时为D0）的值赋值给字W97。然后IR0加1（修改指针），为下一次调用（开始之后为D1，以后依次类推）做准备。注意，W97只在W81.00与W81.01常闭触点均ON才赋值。所以，赋值一次之后，得到了再次出现W81.00与W81.01常闭触点均ON的条件才做新的赋值。这时，正好完成了4个数位的使用。

梯形条4、5、6、7执行数位传送指令MOVD，将根据W81.00与W81.01的变化把W97的0、1、2、3数位传送给W100的数位0。梯形条8、9、10、11、12、13用于处理x、y坐标方向及输出，它的依据就是W101数位0的值。而实际就是预存于D0开始的数表。

梯形条15为终点控制。到了数表结尾将复位W0.10，使工作（W0.10 OFF）停止。图中设定终点数位数（存储字数乘4）为64000，实际可按需要更改。

（3）相对数据列表算法数表生成。可在计算机上用仿真程序生成，生成后下载给PLC。也可使用PLC程序自身生成。这样，PLC使用数表时，可简化计算，提高控制速度。还可人工填入。这对不规则的运动协调控制可能是唯一的方法。好在这些数据可以存储，开头麻烦些，但填入后可长期使用。

4.绝对值数据列表运动控制

除了相对值数据列表，还可用绝对值数数据列表进行运动控制。

（1）绝对数据列表算法要点。把运动轨迹各个坐标的绝对值按步，列写成数表，并存储于PLC的数据存储区（D区）中。PLC程序就是按步，逐次计算数表中相邻“步”之间的差值。并根据差值的符号及大小，确定各个坐标输出脉冲数及输出方向，进而实现运动的协调运动。

（2）绝对数据列表算法实现程序。图4-90所示为这样绝对值数表运动控制程序。该图有17个梯形条。条①为起动与初始化。起动使W5.10 ON后，把D100的地址赋值给索引寄存器IR0及D101的地址赋值给索引寄存器IR1，并使W25（用于计步数）、W60、61、62、63、80、81、82、83（用于计算）清零。同时，调PRV指令，读取脉冲输出口0、1的状态。如果已起动并两个输出口已完成脉冲输出，将按“ON”条件执行梯形条③～（17）间指令。

梯形条②，执行IL指令及把IR0及IR1指向的D字值传送给W50（当前X坐标值）、W51（当前Y坐标值），并使IR0及IR1的值加2（为读取次一坐标值作准备）。这说明D100开始的偶数地址存储的为X坐标值，而奇数地址存储的为Y坐标值。

梯形条③～⑥用以处理X坐标。先是判断次一坐标值是大还是小于当前坐标值。如次一坐标值大，则置“X轴正向”ON，反之置其OFF。同时计算两者的差值，并乘以“计算因子”，确定应该输出的脉冲数。这里的“计算因子”是用以协调输出脉冲数与实际位移的关系。梯形条⑦～⑩用以处理Y坐标。情况类似。

梯形条（11）～（14）用以处理输出脉冲频率及实际输出脉冲。先是比较两个坐标输出脉冲数，然后把“允许最高频率”赋值给脉冲数多的坐标输出口，再按脉冲数比例计算脉冲数小的坐标的输出频率。确保两个坐标输出脉冲频率与输出脉冲数成比例，而且最大脉冲频率还不超过允许值。

梯形条（15）用于计数。当每次脉冲输出完成，都使W25加1。梯形条（16）为终点控制。到了数表结尾将复位W5.10，使工作（W5.10 OFF）停止。图中设定终点步数存于D0中，实际可按需要更改。

（3）绝对数据列表算法数表生成。可在计算机上用仿真程序生成，生成后下载给PLC。也还可人工填入。好在这些数据可以存储，开头麻烦些，但填入后可长期使用。用绝对值数表的优点是，如果是直线运动，填入起点及终点值即可，中间靠输出脉冲数及相应的频率保证。当然，它的精度保证是不如相对值数表。

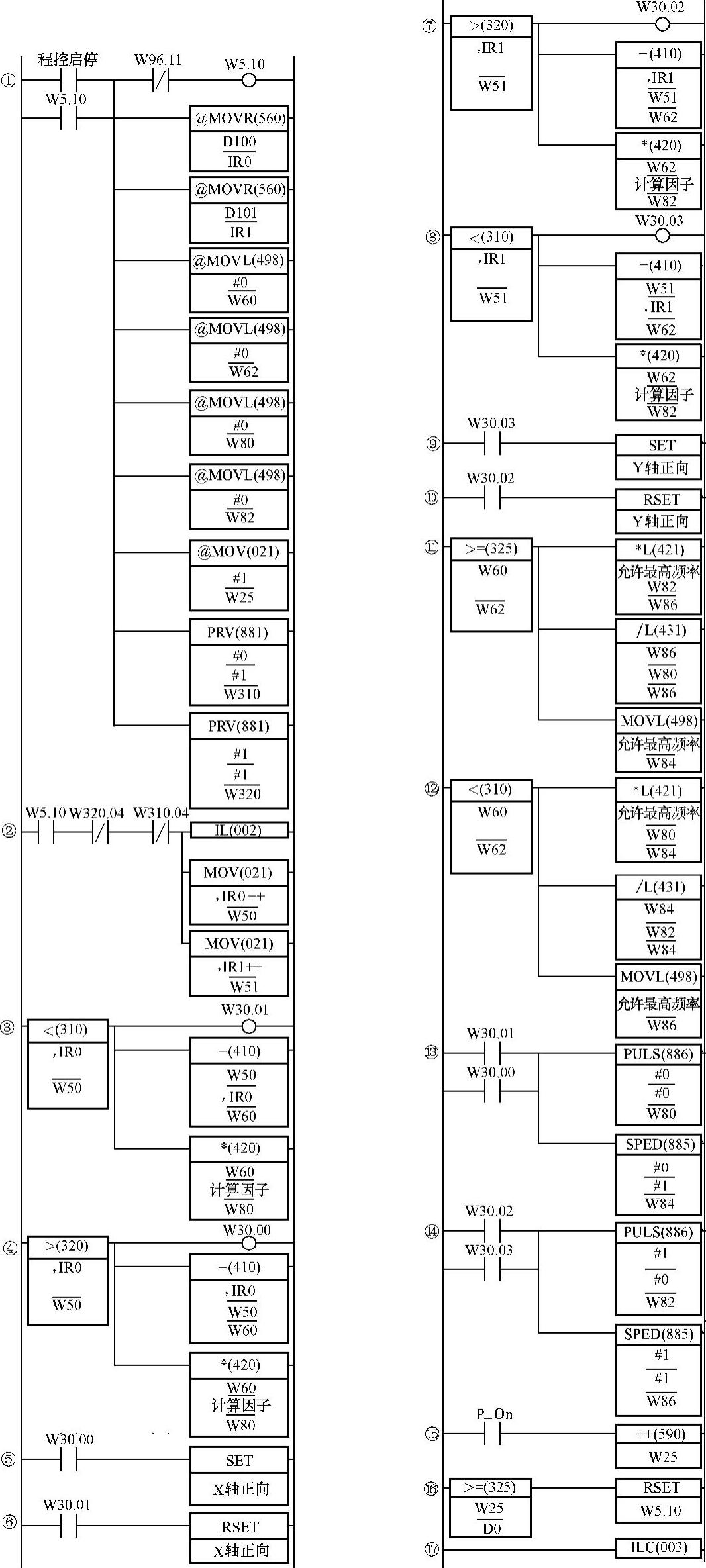
图4-90 绝对值数表运动控制程序