从模糊控制原理知，模糊控制算法的要点是：

从输入到模糊量的转换，也称模糊化；

建立控制规则，进行模糊推理；

从模糊量到输出的转换，也称解模糊（Defuzzification）。

1.模糊化算法

输入量模糊化的任务是把检测到的被控量值转换为相应隶属度的模糊子集。为此，要对输入量（被控量）划分模糊集。如上例输入量有5个模糊子集，即：“太凉”、“凉”、“暖和”、“热”及“太热”。通常按偏差划分，常见的分为7个子集，即负大偏差（NL）、负中偏差（NM）、负小偏差（NS）、零偏差（ZR）、正小偏差（PS）、正中偏差（PM）、正大偏差（PL）。分完子集，还要依经验，确定各个模糊子集的隶属函数。

除了对被控量的值划分模糊子集，如需要，也可对被控量的变化划分模糊子集，如上例，可划分水温很快上升、上升、不变、下降、很快下降等子集，并建立相应的隶属函数。这样，不仅要检测被控量，而且还要检测被控量的变化，用这两者作为控制输入。这样的模糊控制就不是一维的，而是二维的了。

如果把被控量值变化的变化，即被控量的“加速度”，也作上述处理，也作为模糊控制输入，那就是三维模糊控制了。这样的系统当然要复杂些，程序量也大些，但控制的效果肯定要好些。

显然，这里的“划分模糊集”与“建立隶属函数”都要靠经验。没有经验，这个“划分”与“建立函数”是难以实现的。

有的被控系统的被控量不止一个，而是两个或多个。则应把各被控量分别作相应的模糊化，都作为模糊控制输入。这样的模糊控制系统就不是单变量的，而是多变量的了。

不管是一维、二维或三维，还是单变量或多变量，模糊化总是先划分模糊子集，然后再建立其隶属函数。实现的方法都是用以上算法，设计PLC程序或使用PLC专用模块，靠PLC运行程序，把检测到的被控量的值转换为相应模糊子集的隶属度。

2.模糊推理算法

模糊推理的任务是，根据当前输入的不同隶属度的模糊子集，遵照预先设定的规则，推断应有的模糊控制输出。这些也是通过运行PLC程序或用PLC专用模块实现。

模糊推理依据是规则。常见的规则大体有：

“如A则B”型，可写成：

IF A THEN B（如果A成立，那么B成立）

“如A则B否则C”型，可写成：

IF A THEN B ELSE C（如果A成立，那么B成立；否则C成立）

“如A且B则C”型，可写成：

IF A AND B THEN C（如果A成立，同时B也成立；那么C成立）

“如A或B则C”型，可写成：

IF A OR B THEN C（如果A成立，或如果B也成立；那么C成立）

……

注意，这里的A、B、C都是模糊量的集合。如果小前提为A1，与大前提A不完全一样，是否能推断出有价值的结论？这在传统逻辑推理中是不可能的。而用模糊逻辑推理则是可能的。如下显示的即为它的推理过程：

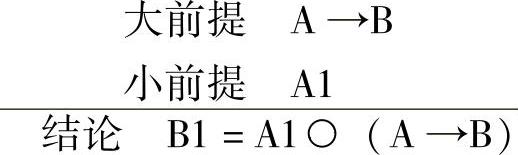
这里符号“○”为矩阵乘。

以下还是以洗澡水温度控制为例，看看，有了“如A则B”这个大前提后，是怎么进行模糊推理的。

这个大前提就是，水的状态（如“太热”等模糊子集）与控制输出（如“ZLL”等子集）间的关系R。以上已介绍过，这是凭经验得出的。这个关系可用以下矩阵表达。这里“0”、“1”代表的是关系隶属度。

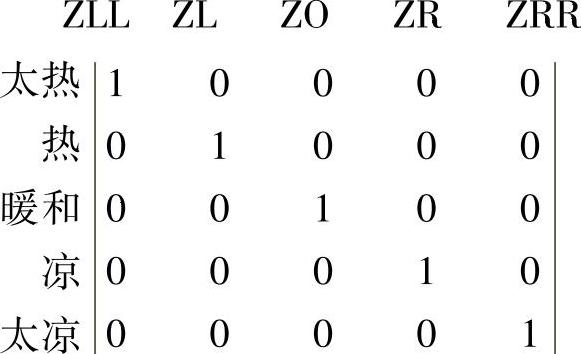
小前提Al如为“太热”，即

Al= 1 0 0 0 01

则Bl=Al○ORo即(www.daowen.com)

根据矩阵运算规则可知，这时B1=10000。即仅“ZLL”子集的隶属度为1，其他的均为0。

小前提A1如不正好是“太热”，而是在“太热”与“热”之间，如水温为70℃，如图3-89所示。即

A1=0.50.5000，则

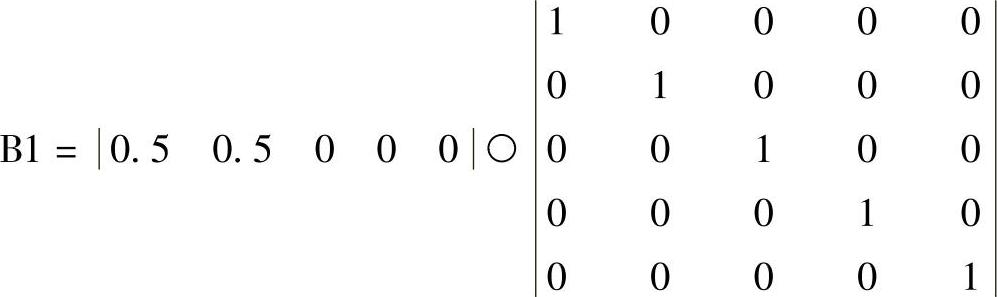
根据矩阵运算规则可知，这时B1=｜0.50.5000｜。即“ZLL”子集的隶属度为0.5，“ZL”子集的隶属度也为0.5，其他的均为0。

对“如A则B否则C”型的推理，其“IF A THEN B”部分，与上相同。“ELSE C”部分，要用到模糊非隶属度的运算。这个运算较简单，即

A非的隶属度=1-A的隶属度

A1非的隶属度=1-A1的隶属度

有了这个关系，其推理过程可描述如下：

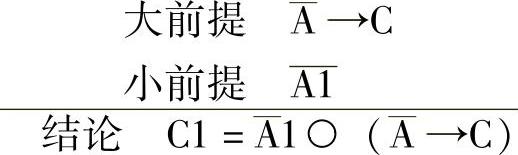
这里符号“○”也是矩阵乘。再往下的处理与上类似，就不再赘述了。

对“如A且B则C”型及“如A或B则C”型的推理，如弄清模糊逻辑“与”及模糊逻辑“或”的算法，进一步处理也就不难了。

模糊逻辑“与”，其符号为“∧”，如：D=A∧B，则D的隶属度为A、B小者，即按最小原则定其隶属度。

模糊逻辑“或”，其符号为“∨”，如：D=A∨B，则D的隶属度为A、B大者，即按最大原则定其隶属度。

有了这些关系，其推理的进一步处理也与上类似。

从以上介绍可知：

1）模糊推理的算法是确定的，因此总可用PLC相应程序予以实现。

2）有了这个推理方法，同一大前提，但小前提不同，也可推出相应的不同结论。显然，有了它可减少规则数。

3）推理的结论仍是模糊子集，要用于输出，还要解模糊处理。

提示：有的系统输入输出关系不是线性的；有的还有时滞，甚至是大滞后；有的还是不确定的或无法建模的等。这对基于经验总结出的语言型规则，去实现进行控制的模糊控制来说，是无关紧要的。完全可建立相应的控制策略予以实现，并可得到应有的效果。

3.解模糊算法

模糊推理的输出仍是模糊量，是输出模糊子集。要用它作控制输出，必须把这个输出模糊子集按照一定算法转换为确定量的控制输出。这也就是解模糊。

为此，首先，要确定控制输出的类型。有两种控制输出：比例输出，积分输出及这二者相结合输出。

比例输出是把解模糊求得的值，直接用作控制输出。它响应快，但它的控制是有“静差”的。

积分输出是把解模糊求得的值，与当前控制输出先进行代数和，然后再用这个和作控制输出。它为“无静差”控制，但响应慢，且有可能超调或振荡。

也把这二者相结合，在一定情况下用比例输出，在另一情况下用积分输出。这样，有时可取得更好的效果。

其次，还要确定解模糊方法。有多种方法：如最大隶属度法、中位数法、加权平均法、估值法、重心法及求和法等。较常用的为最大隶属度法、加权平均法。

最大隶属度法比较简单，选择出哪个隶属度最大，就用与其对应确定值用作输出。加权平均法就是按隶属度加权平均，把这样求得的值用作输出。

总之，解模糊实际是一些数据处理问题。这对具有较多运算指令的PLC处理起来是不难的。