在闭环负反馈控制系统中，系统的偏差信号e（t）是系统进行控制的最基本的原始信号。为了提高控制系统的性能指标，可以对偏差信号e（t）进行改造，使其按照某种函数关系进行变化，形成所需要的控制规律P，从而使控制系统达到所要求的性能指标，即

u（t）=f［e（t）］

所谓PID控制，就是对偏差信号e（t）进行“比例加积分和加微分”形式的改造，形成新的控制规律u（t）。PID是比例（P）、积分（I）、微分（D）之意。标准PID的控制值是与偏差（设定值与实际值之差）、偏差对时间的积分、偏差对时间的微分，三者之和成正比。如用式子表示，即

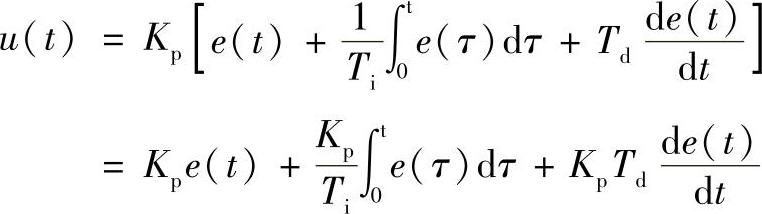
式中 K_pe（t）——比例控制部分，K_p称为比例常数；

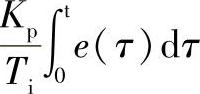——积分控制部分，T_i称为积分时间常数；

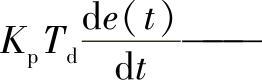微分控制部分，T_d称为微分时间常数。

在零初始条件下，将上式两边取拉普拉斯变换，可得

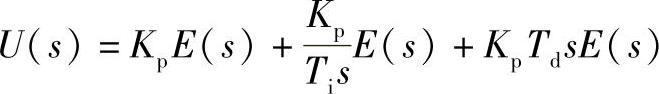
基于PID控制的闭环负反馈控制系统的传递函数框图如图3-41所示。

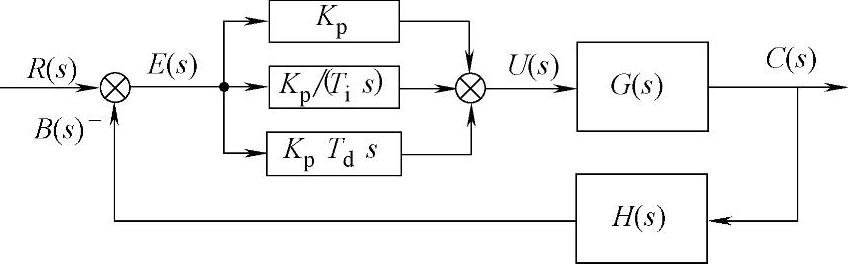
图3-41 基于PID控制的闭环负反馈控制系统

上式用于连续系统的PID控制。如在PLC控制中用它，则必须将其“离散化”，用相应的数值计算，代替这里的积分、微分。(www.daowen.com)

设采样周期为T，将前述PID控制规律u（t）进行离散化处理，可得PID控制的第k个采样周期的离散算法u（n）为

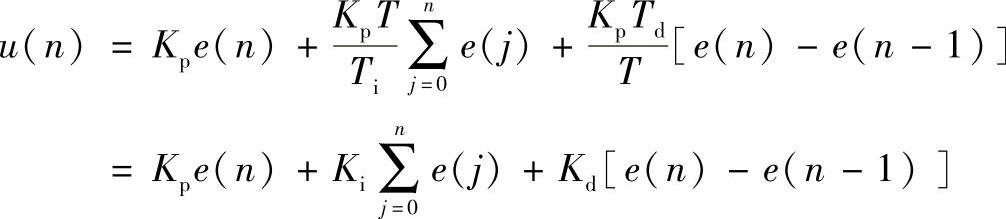
其中，比例控制部分K_pe（t）离散化为K_pe（n）。

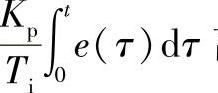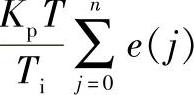积分控制部分离散化为。令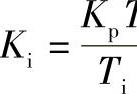，并称为积分控制部分的加权系数。

微分控制部分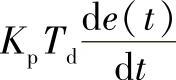离散化为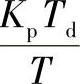［e（n）-e（n-1）］。令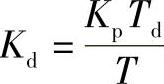，并称为微分控制部分的加权系数。

根据PID控制的位置式离散算法，可得PID控制的第n-1个采样周期的位置式输出u（n-1）为

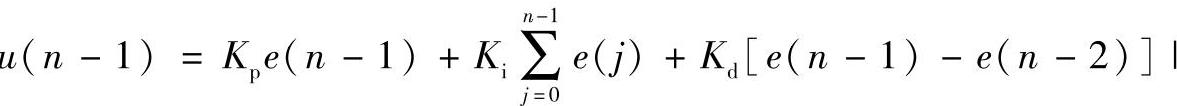
将上述两式u（n）与u（n-1）相减，可得PID控制的第n个采样周期的增量式离散算法Δu（n）=u（n）-u（n-1）为

Δ_u（n）=K_p［e（n）-e（n-1）］+K_ie（n）+K_d［e（n）-2e（n-1）+e（n-2）］

于是可得PID控制的第n个采样周期的位置式输出u（n）为

u（n）=u（n-1）+Δu（n）