图3-39表示了无静差控制的算法框图。这种控制可完全消除静差。与图3-37不同的只是，这里的控制值不是由偏差E与“设定值”相加产生，而是在每进行一次此类运算时，自身与偏差E相加。这样，可实现即使无偏差，但也可使R大于设定值为R₀，实现补充控制。

图3-39 无静差控制算法框图

图3-40为与图3-39对应的梯形图程序。

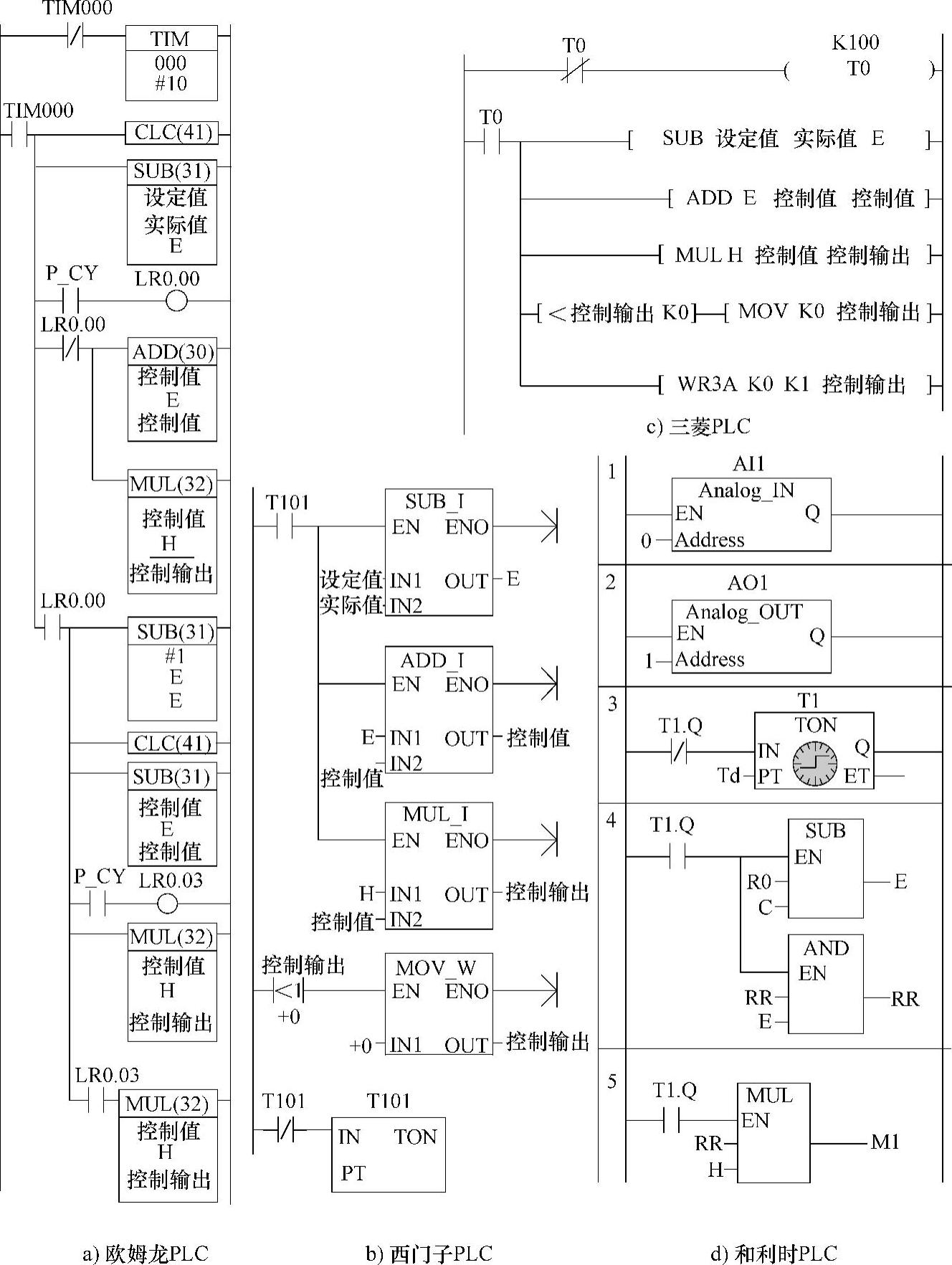
图3-40 无静差控制梯形图程序

从图3-40a可知，当“无静差控制”ON，则执行如图程序。先是定时器TIM 000工作。每1s，其常开触点TIM 000 ON一次，则控制程序执行一次。这么做的目的是，控制输出改变后要等待一定时间再处理，以适应系统时延特性。否则会出现超调，以至于系统振荡。这里定时间隔为1s，如系统时延较大，还可加大。本程序与图3-33程序不同的只是用E与“控制值”累加（或累减），代替E与“设定值”的加（或减）。

图3-40b、c、d与其不同的只是用十六进制数，且也没有进位位参与计算问题。(www.daowen.com)

图3-40d中节1、2为使能模拟量输入、输出模块。节3为调用定时功能块，以产生定时脉冲。并用其去起动误差累加运算。节4、5进行偏差累加，即无偏差控制计算。当然，这里变量须与模拟量输入、输出通道地址关联。如果必要，还要作些数值换算。

由于这里用了累加、累减，相当于加入积分环节。所以，只要存在偏差，即“设定值”减“实际值”不为0，那么，每进行一次运算都将使“控制值”变化。直到“控制值”变化到使系统实际值等于设定值时，即“设定值”减“实际值”为0，不存在偏差时，“控制值”才保持不变。这也就实现了设定值对系统的无静差控制。

无静差控制可消除所有由干扰产生的误差，这是它的优点。但同样存在系统能否稳定工作的问题。而系统要是不稳定，那即使静态精度再高，也是不允许的。所以，还得寻找更好的控制办法。以下将介绍的PID控制就是一个较好的办法。

提示1：离散系统闭环控制振荡有两种原因：静态原因及动态原因。

提示2：静态原因是系统离散性。系统离散，就不可能任意要求的调节量都存在。如设定值正是这个不存在调节量，那是永远做不到的。而硬要这么做，只好振荡了，即出现调节量一会儿比设定值大，一会儿比设定值小，总也稳定不下来。正如，要买1斤鸡蛋，很难做到买的正好是一斤，要不稍多一点，要不就是稍差一点。显然，提高分辨率（如鸡蛋很小）可减少这个振荡。

提示3：动态原因是系统惯性、时延。前者在实际的系统中也总是存在的。减少惯性，减少时延，选择合适放大倍数，可避免出现振荡。