图1-163所示为本书绪论中提到求实现欧几里德算法的子程序。

它是实现欧几里德算法中，在花括弧内的算法。对图1-163a到了余数ZZ（DM7、VW8、D7或remainder）为0时，即EQ或pEQ ON时，则输出公因数。否则，一直进行相应运算。这里XX，YY为形式参数。调子程序前用X，Y对其赋值。

提示：DIV指令为整除运算指令。如图1-163a，其商存于DM6中，而余数存于DM7中。图1-163b，其商存于VW6中，而余数存于VW8中。图1-163c，其商存于D6中，而余数存于D7中。故判断DM7或VW8或D7是否为0，即可知道YY能否XX整除。图1-163d节1为求“模”运算。目的是得到余数。节2是判断得到的余数是否为0。节3、4是如果余数为0，输出结果（Common Factor），并返回主程序。节5如果余数（remainder）不为0，变换求“模”运算数据，为下一次被调用的新计算作准备。

图1-164为实现欧几里德算法的主程序。

它是实现欧几里德算法中，花括弧外的算法。AA为求解起动信号，一旦它ON，将使pAAON一个扫描周期，并用它去起动bAA或call＿calculate，进而调上述子程序。直到EQ或图1-164d的pEQ ON（即zz=0），并通过pEQ使bAA或call＿calculate OFF，则退出子程序调用。图1-164d的pEQ不是微分输出，所以，图1-164d第1节增加了它的复位操作，即call＿calculate

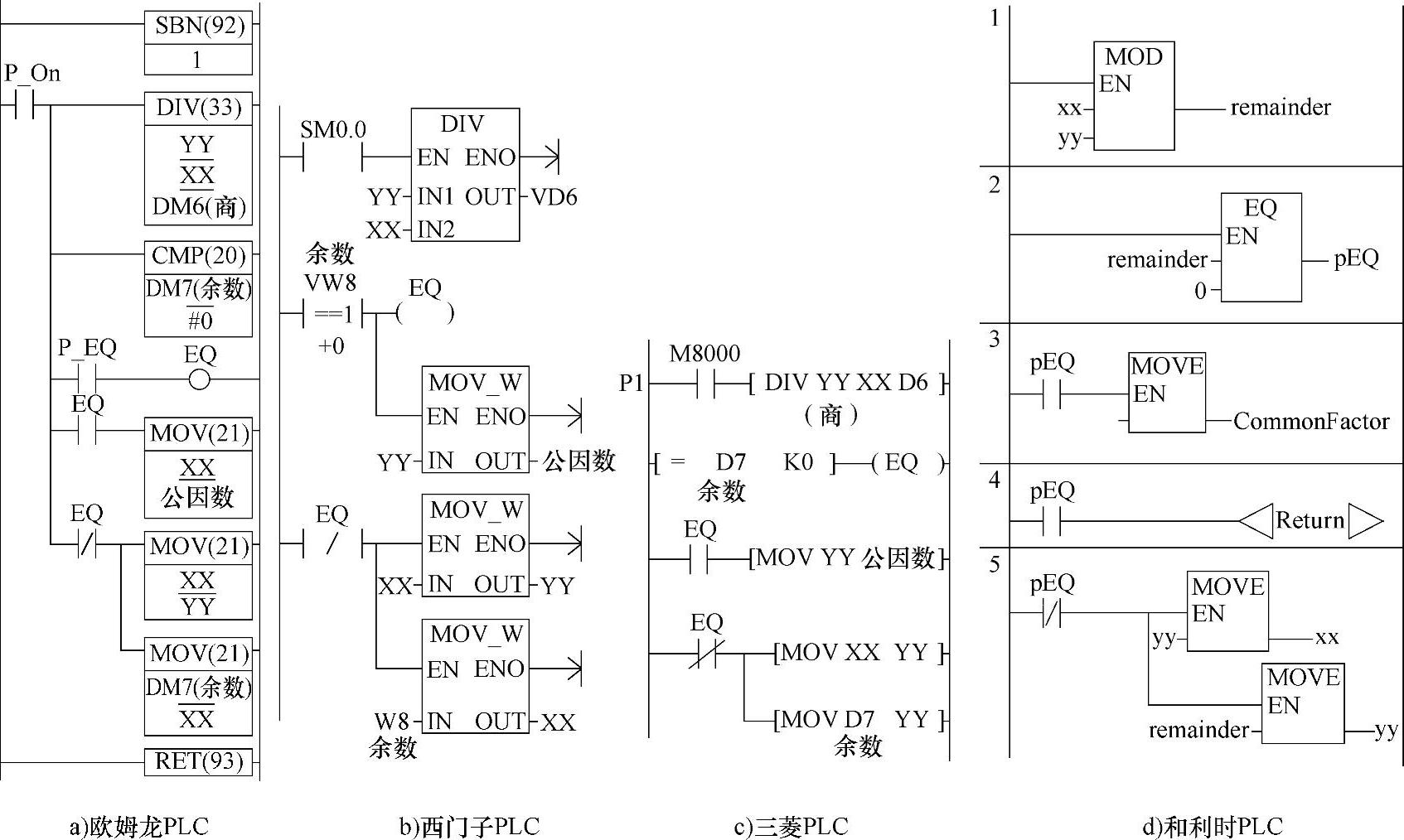
图1-163 求两个整数的公因数子程序(www.daowen.com)

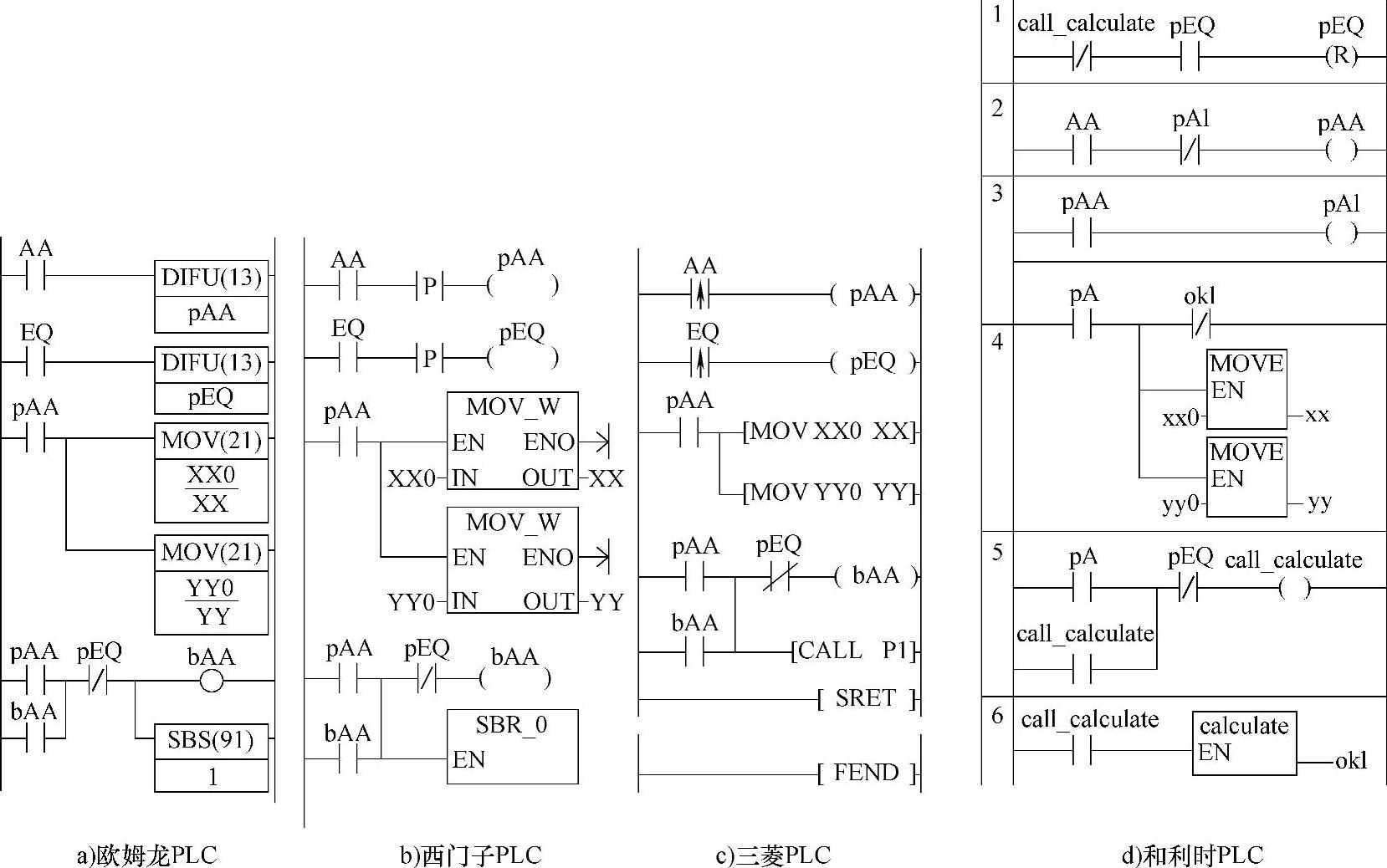
图1-164 求两个整数的公因数主程序

OFF后，如pEQ ON，自身将复位。这也为新的计算作准备。

提示：图1-164程序用了微分指令及bAA或call_calculate的自保持功能，目的是确保在pEQ OFF，即yy未能被xx整除时，子程序一直在调用。而到了EQ ON，即yy能被xx整除时，又可使bAA OFF，子程序停止调用。在多周期完成运算的情况下，这么处理是很方便的。

显然，在实现上述算法时，就有指令的选用及资源的利用两个问题。