在电机起动和低速运行时,基于优化矢量表的DTC会经常选用零矢量,由于此时定子电阻压降不可忽略,而优化矢量表的建立为了便于分析通常忽略定子电阻压降,从而导致定子磁通的跌落[40]。图7-52所示为采用优化矢量表的三电平DTC运行在稳态30r/min时的空载波形。可以看出,定子磁链出现了波动而且幅值未达到额定值,这正是采用滞环控制在低速时选用了较多零矢量所致。
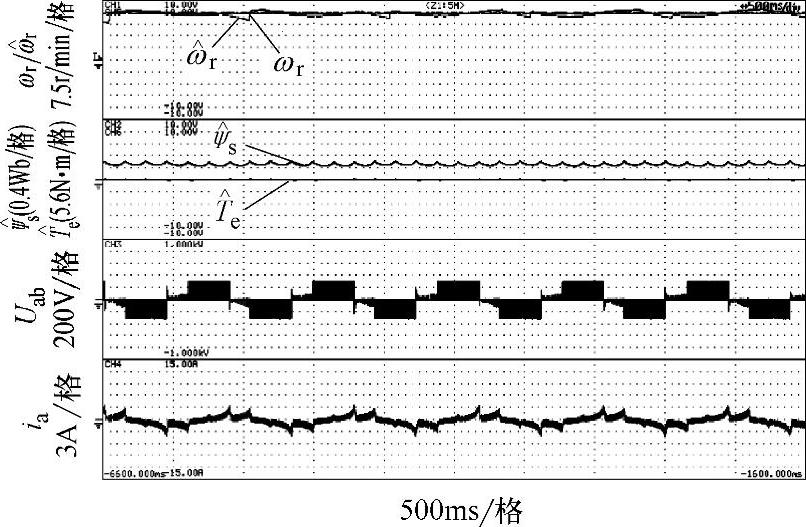
图7-52 30r/min空载稳态波形
为了改善低速特性和起动性能,20世纪90年代初德国鲁尔大学在Depenbrock教授和Steimel教授的领导下提出来间接转矩控制(Indirect Torque Control,ITC),将砰砰控制改为连续的调节器[45],通过比较磁链和转矩的指令值和实际值的差,从而得到目标电压指令,然后再通过SVPWM发出脉冲。
假设在第k个采样时刻定子磁链矢量为ψs(k),希望下一时刻定子磁链矢量达到给定值,即ψs(k+1)=ψ∗s(k),则相应的磁链幅值增量Kψ和相位增量Δθk如图7-53所示。
在知道磁链幅值和相位增量后,定子磁链增量计算公式为
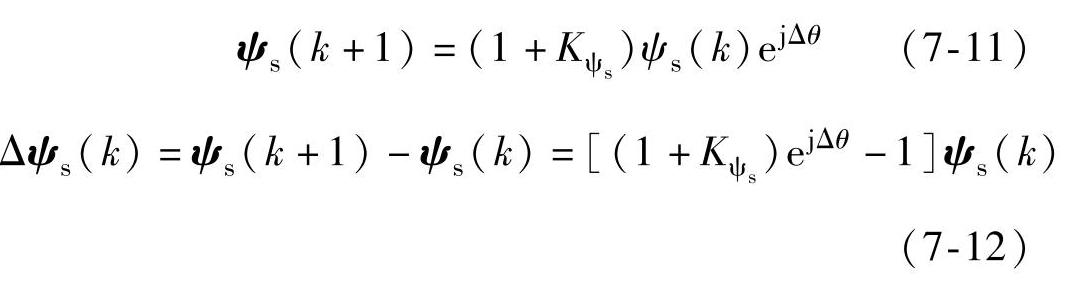
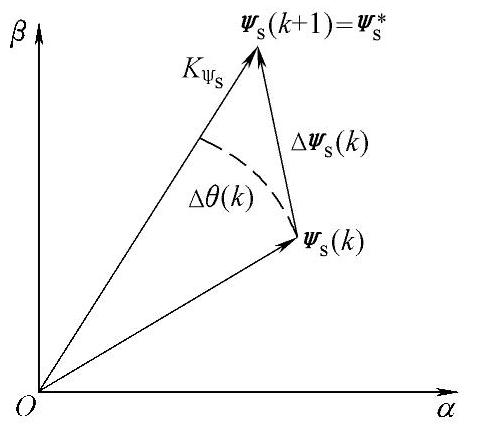
图7-53 定子磁链增量
由式(7-1)可得期望的下一时刻的电压矢量为(https://www.daowen.com)
us(k+1)=Rsis(k)+Δψs(k)/Ts (7-13)
另外,相位矢量增量由两部分组成:磁链旋转引起的静态部分Δθs和转矩变化引起的动态部分Δθd。Δθd由给定转矩和实际转矩的误差通过PI控制器后得到。Δθs计算公式为
Δθs(k)=(ωr(k)+ωsl(k))Ts (7-14)
式中
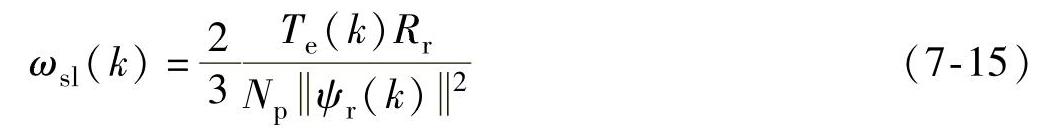
在无速度传感器运行下,速度、转矩和磁链都通过基于转矩观测的龙贝格观测器估计得到。本节采用的系统框图如图7-54所示,其中转速环采用FLC。

图7-54 ITC控制框图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






