扩展卡尔曼滤波（EKF）是线性卡尔曼滤波算法在非线性系统的扩展应用。由于EKF可以在系统含有噪声的情况下得到对系统状态的准确估计，非常适合用于电机的状态观测。国内外有很多文献对此进行了研究，但有些只给出仿真结果^[13-14]，或者仅在简单的开环恒u/f比条件下进行实验^[14-15]，而未把估测转速真正用于闭环控制中独立运行。参考文献[15]引入了转矩观测，提高了低速时的观测精度，但其实验是基于精确的电机参数和转动惯量，并未深入考察转动惯量变化时对转速观测的影响，而且其实验条件是在开环恒u/f比条件下完成，系统的动态响应很慢。

本节在直接矢量控制系统采用EKF来估计转速和磁链并用于闭环控制中。EKF的算法比较复杂，不少文献^[15-16]都采用浮点DSP来进行实验，使得系统成本较高。本节介绍和考察了5阶和带负载转矩观测的6阶EKF^[17]，针对EKF的实现过程和参数调试进行了详细的说明。

1.基本原理

考虑一般的离散非线性系统，设其状态方程为

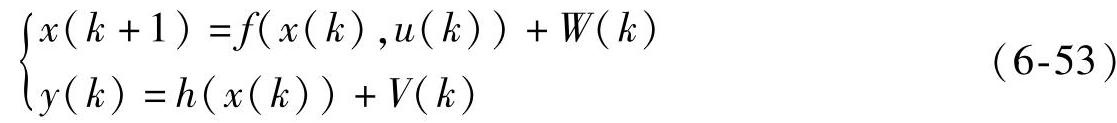
式中 u（k）——系统输入；

W（k）——系统噪声；

V（k）——观测噪声，假设两者是互不相关的零均值高斯白噪声，且有cov（W）=E{WW^T}=Q，cov（V）=E{VV^T}=R。Q和R分别是W（k）和V（k）的协方差矩阵。定义如下雅可比矩阵，其中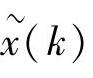是状态预报值。

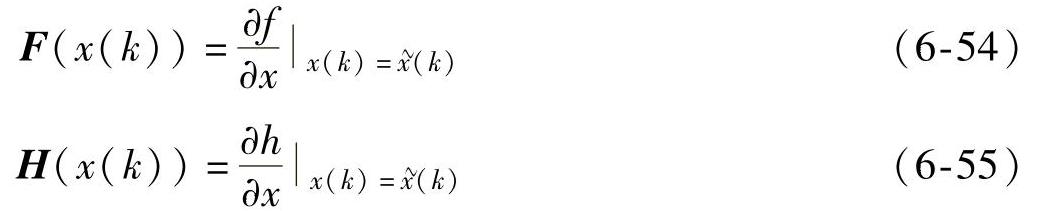
将式（6-53）在状态估计值附近泰勒展开，略去高于一次的项，可以得到式（6-53）的线性化模型

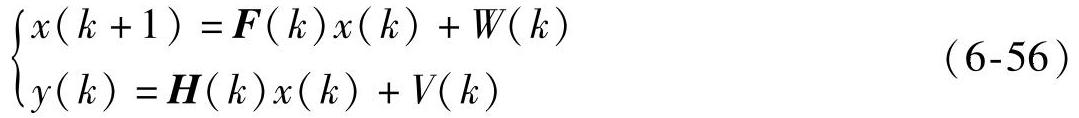
将非线性系统线性化后就可以利用线性卡尔曼滤波的递推公式来进行状态估计。通常包括两个阶段：

1）预报阶段。由系统模型和上一时刻的状态来计算下一个状态预测值，同时还要计算状态协方差矩阵的预测值。

2）滤波阶段。通过增加误差校正项，从状态预测值得到下一个状态估计值，同时还要更新状态误差协方差矩阵。

扩展卡尔曼滤波的一般步骤总结如下^[13-18]：

（1）计算状态预测值

（2）状态协方差矩阵

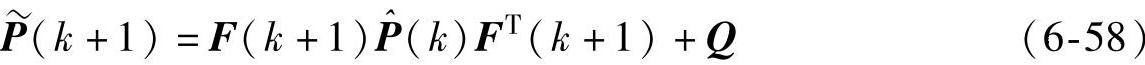
（3）计算卡尔曼增益矩阵

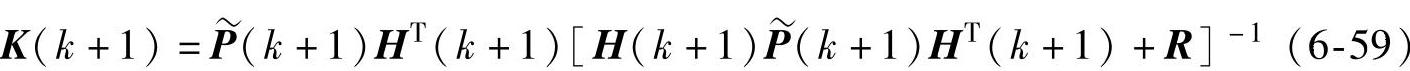
（4）估计状态矢量

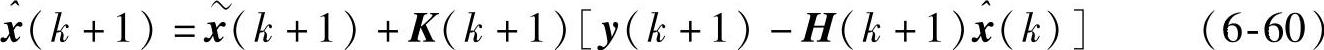
（5）更新状态协方差矩阵

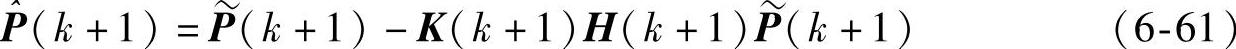
式（6-57）～式（6-61）中凡是加上标“～”的表示预测值，加上标“^”的表示估计值。

2.基于静止坐标系的扩展卡尔曼滤波

EKF可用于电机控制中观测磁链和转速，在具体实现时可采用静止坐标系，也可以采用转子磁场定向的同步旋转坐标系，二者各有优缺点^[19]。选择同步坐标系时，定子电压和电流的测量值必须通过旋转坐标系变换转换到同步坐标系上，在变换矩阵中用到与转子磁场矢量空间角度相关的三角函数，增加了系统模型的非线性，也增加了系统迭代计算时间，相关初值矩阵的选择也更加没有规律，系统的稳定性得到了削弱。而采用静止坐标系，省掉了输入电压和电流的旋转变换，降低了系统的非线性复杂程度，系统的稳定性得到了提高^[20]，不足之处是系统的阶数与同步坐标系相比要提高一阶，增加了系统实时实现的计算量。对于观测器来说，稳定性很重要，所以这里采用基于静止坐标系的EKF。

令式（5-4）中ω_k=0并展开成分量形式，可得电机在静止αβ坐标系下的数学模型为

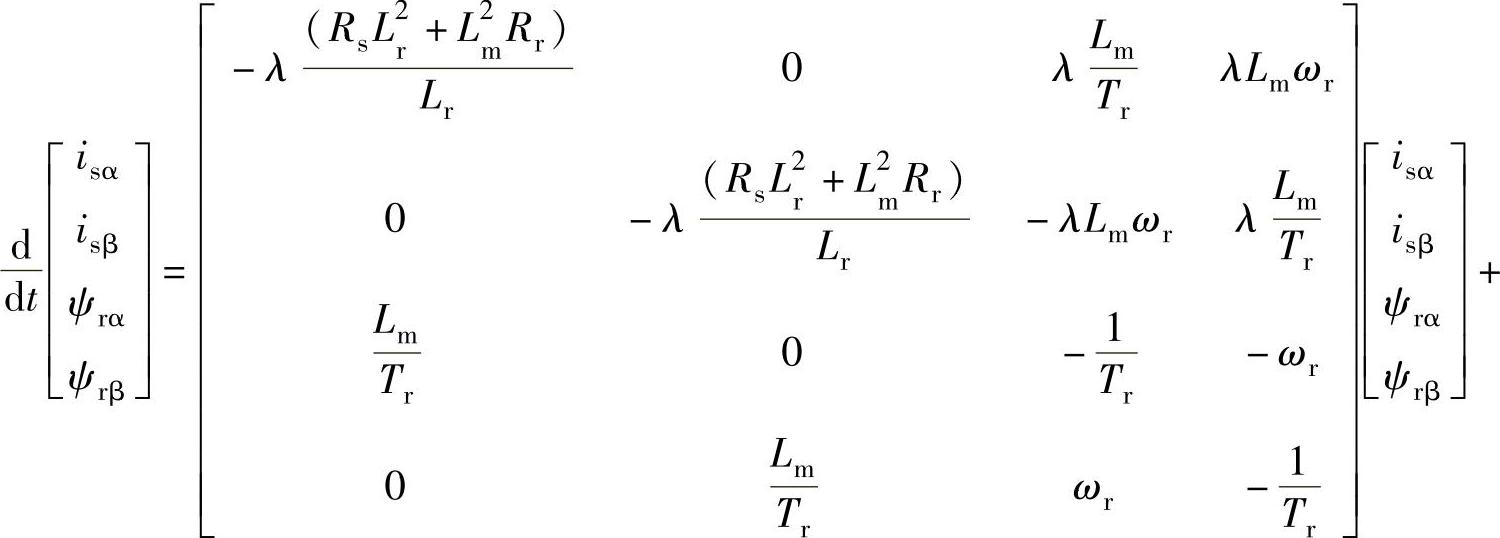
当转速已知时，式（6-62）所示电机模型是线性模型，在无速度传感器控制中转速未知，方程变为非线性。为辨识出转速，将其也看成一个状态变量，就可以得到一个五阶的增广电机模型。这时状态变量为x=[i_sαi_sβψ_rαψ_rβω_r]^T，相应的增广电机模型为

式中

(www.daowen.com)

在采样周期很小或负载转动惯量很大时转速的变化可以忽略不计，故式（6-63）中假设dω_r/dt=0。在扩展卡尔曼滤波观测器中，可将这种忽略引起的误差作为系统噪声处理，在递推计算中给予必要的校正。

将式（6-63）离散化可以得到

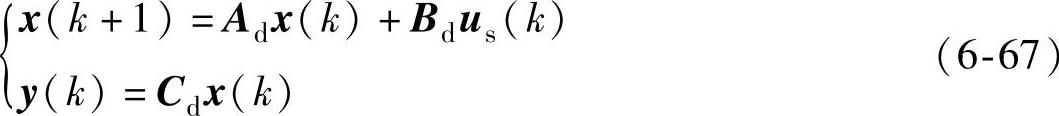
式中

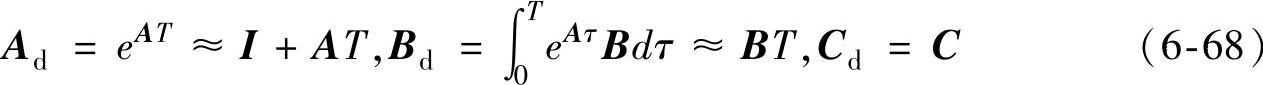
由式（6-54）和式（6-55）可以得到离散化后的增广电机模型的雅克比矩阵为

将式（6-67）～式（6-70）代到式（6-57）～式（6-61）中就得到了异步电机的卡尔曼滤波迭代公式，在辨识转速的同时可以观测磁链。

3.引入转矩观测的扩展卡尔曼滤波

无转矩观测的5阶EKF模型中假设dω_r/dt=0，引入转矩观测后负载转矩也作为状态变量，这时状态变量为x=[i_sαi_sβψ_rαψ_rβω_rT_L]^T，忽略电机运动方程中的摩擦系数，相应的增广电机模型需要在式（6-62）的基础上再增加式（6-71）所示的两个方程：

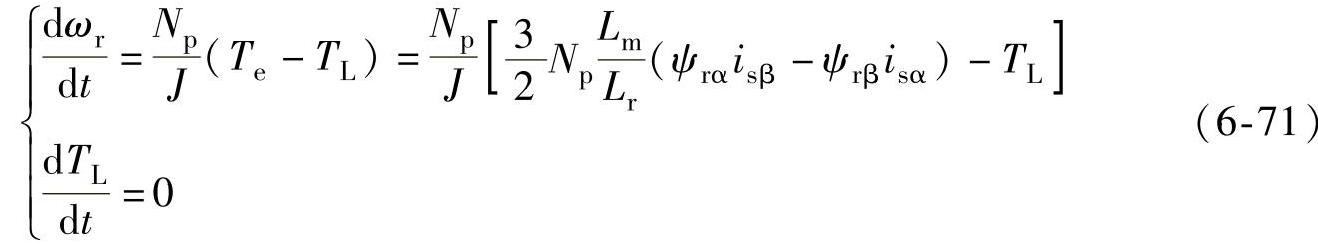
由于负载的精确动态特性通常是未知的，在采样周期很小时负载的变化可以忽略不计，故式（6-71）中假设dT_L/dt=0。在扩展卡尔曼滤波观测器中，可将这种忽略引起的误差作为系统噪声处理，在递推计算中给予必要的校正。

将式（6-62）和式（6-71）所对应的增广电机模型离散化，代入到式（6-54）和式（6-55）中可以得到离散化后的增广电机模型的雅克比矩阵为

将上述结果代到（6-57）～式（6-61）中就得到了引入转矩观测的异步电机扩展卡尔曼滤波迭代公式。

4.EKF参数调试

EKF状态估计的关键是确定式（6-59）中的增益矩阵K（k+1），而增益矩阵的确定又取决于Q、R和P的初值。假定噪声矢量V和W是不相关的，则可以确定Q和R都是对角阵。P是估计状态矢量的协方差矩阵，P的初值P₀只影响暂态过程中转速估计的振幅，对暂态持续时间和稳态性能影响不大^[21]，通常取P₀为单位阵。

Q是系统噪声的协方差矩阵，它包括了电机模型本身的不准确、电机参数的不精确以及运行过程中的变化、系统扰动等。另外，定点DSP的有限字长在实际计算过程中所引起的舍入和截断误差，也可以认为是系统噪声。增加Q就是相应地加强系统噪声，或者增加了系统的不确定性。与此同时，滤波增益矩阵的元素也会增大，相当于加强了测量反馈的作用，使得滤波器瞬态响应变快。对于5阶EKF，Q取为diag[q₁，q₁，q₂，q₂，q₃]；对6阶EKF，Q取为diag[q₁，q₁，q₂，q₂，q₃，q₄]。其中，q₁、q₂、q₃和q₄分别对应电流、磁链、转速和转矩。为了简单和便于调试，认为α和β轴分量的噪声一样，这样就只需确定3个或4个常数。

R是测量噪声的协方差矩阵，它反映了传感器测量、A/D转换和定点DSP有限字长表示等所引入的测量噪声的特性。R变大，表明系统测量值受干扰较大，即测量的不确定性增加，减小R会导致瞬态特性变慢。由于电流测量采用的是同一个DSP上的AD，认为其噪声特性一样，并且与q₁相同，即R=diag[q₁，q₁]。

本节考察了Q和R的参数变化对转速估计的影响。首先针对静止坐标系下的5阶EKF进行了研究，图6-28a～图6-28d分别考察了q₁、q₂和q₃变化对转速估计的影响。在图6-28a中固定q₂=1e-4，q₃=20，然后变化q₁，结果表明q₁越小动态跟踪响应越快，但同时稳态精度降低，在预励磁即转速为0阶段有较大估计误差，q₁越大则稳态精度越高，但有较大时延，q₁在（0.01，5）区间变化时都可以使系统稳定。在图6-28b中固定q₁=0.3，q₃=20，然后变化q₂，得到与q₁类似的结果，只不过使系统稳定的q₂变化范围是（1e-5，1e-2）。在图6-28c中固定q₁=0.3，q₂=1e-4，然后变化q₃，得出的结果与q₁和q₂恰恰相反，q₃越小则稳态性能越好，但时延越大，而q₃变大时则动态性能增强，稳态精度降低，其稳定工作范围是（1，100）。

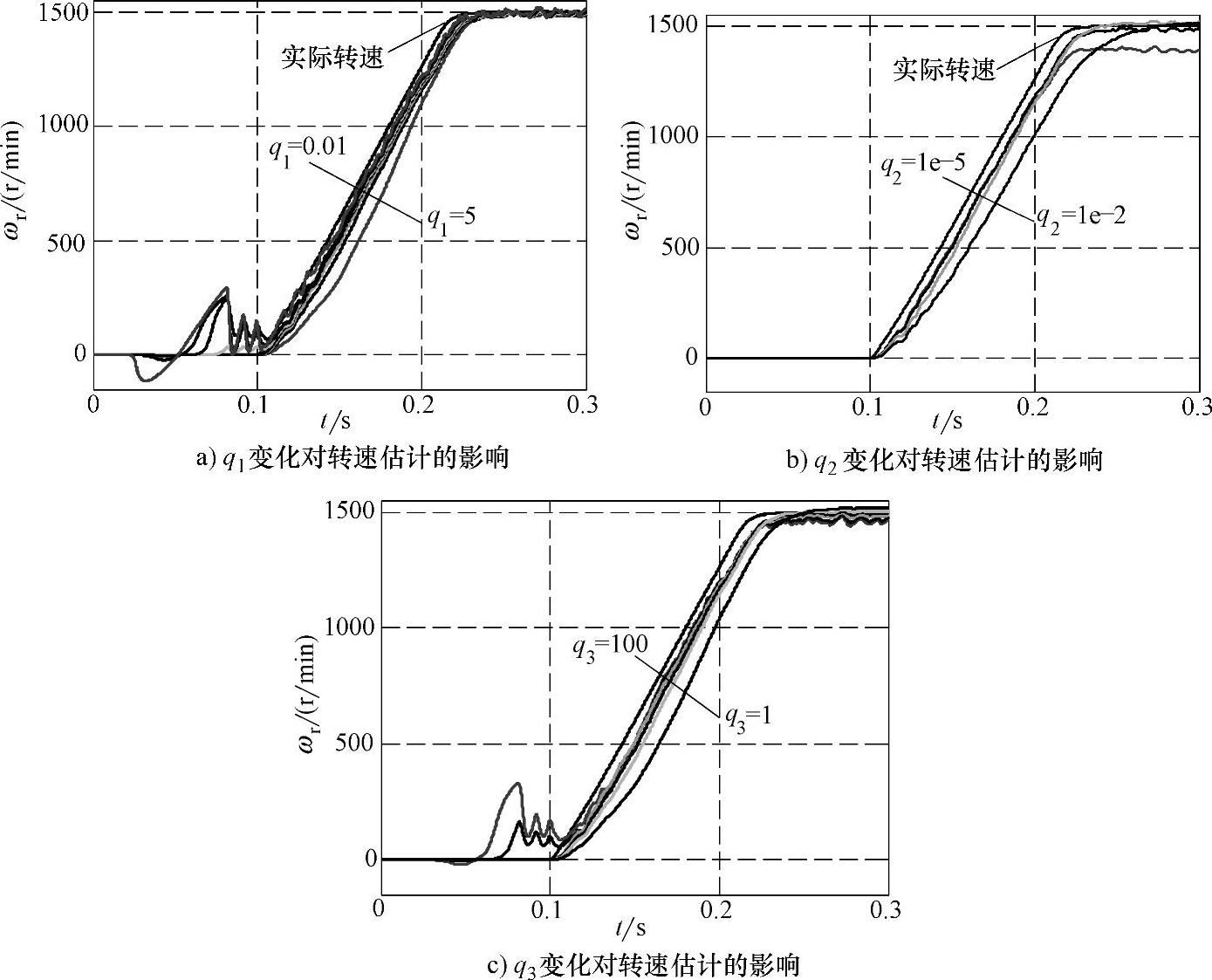
图6-28 Q值变化对转速估计的影响

另外，还考察了6阶EKF中Q值变化对负载转速估计的影响。在图6-29a中固定q₁=0.3，q₂=1e-4，q₃=1，图6-29b中固定q₁=0.3，q₂=1e-4，q₃=10，然后变化q₄，结果表明q₄越小动态跟踪响应越快，但同时稳态精度降低，在预励磁即转速为0阶段有较大估计误差，q₄越大则稳态精度越高，但有较大时延，q₄在（0.01，0.5）区间变化时都可以使系统稳定。

5.仿真结果

在MATLAB/Simulink中进行了仿真，电机参数和仿真条件同6.2.1节第5部分。首先考察了5阶EKF的性能，采用的协方差矩阵为Q=[0.3，0.3，1e-4，1e-4，10]，R=[0.3，0.3]，其仿真结果如图6-30所示。采用引入转矩观测的6阶EKF仿真结果如图6-31所示，采用的协方差矩阵为Q=[0.3，0.3，1e-4，1e-4，10，0.1]，R=[0.3，0.3]。对比二者转速波形可以看出，后者具有更小的动态延迟，转速估计更加准确，说明引入电机运动方程后，转速估计的稳态精度，尤其动态响应得到了提高；磁链估计二者相差无几，仅在开始预励磁阶段估计磁通和实际磁通有所偏差，之后估计磁链很快收敛到真实磁链。

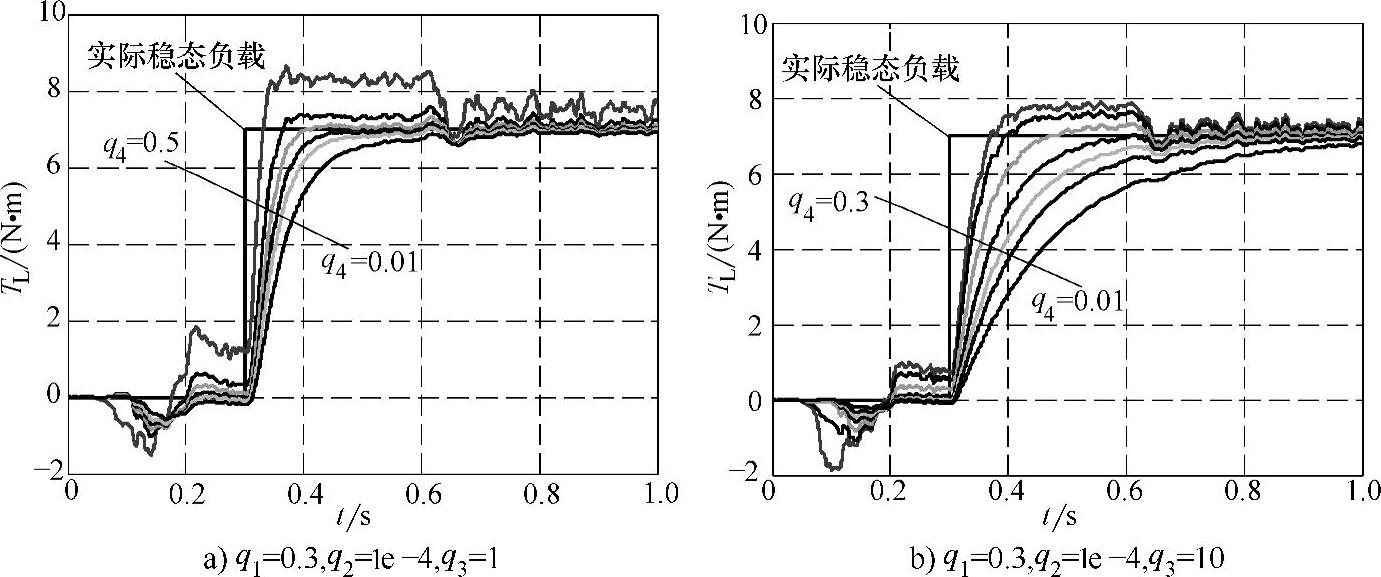
图6-29 q₄变化对负载转矩估计的影响

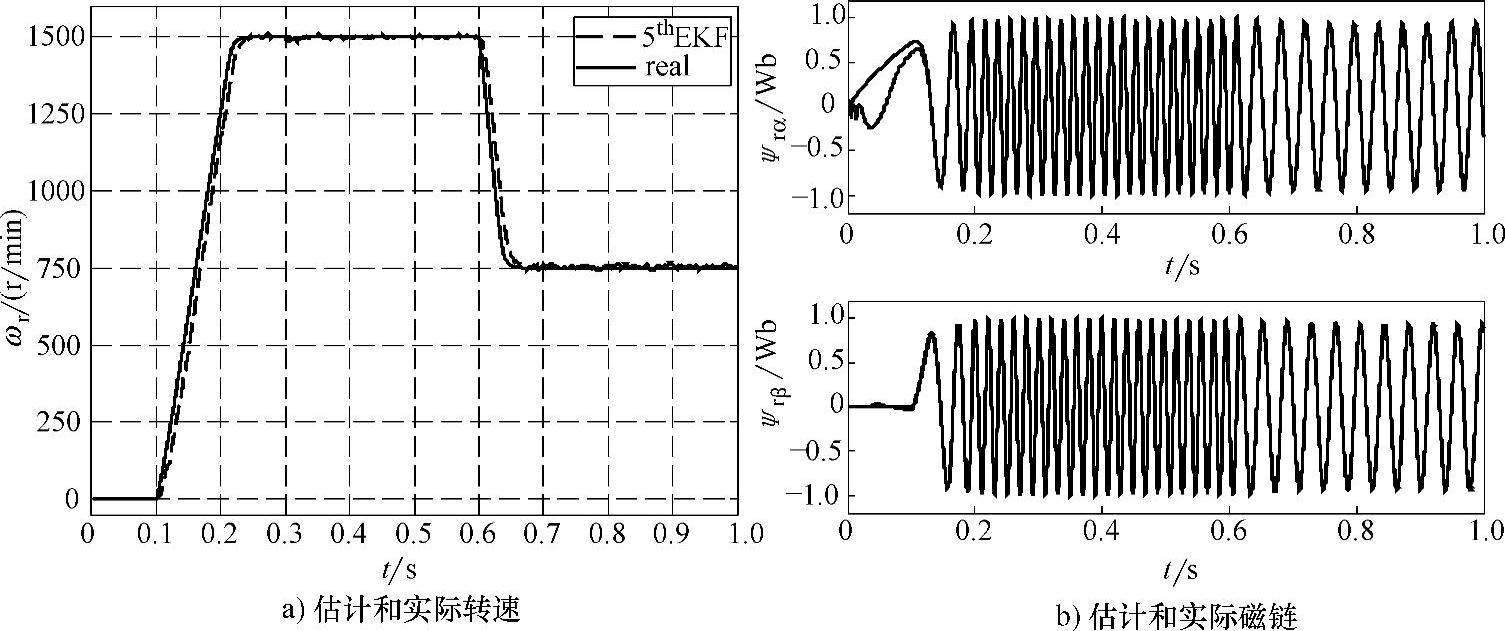
图6-30 5阶EKF转速和磁链观测结果

图6-31所示是在精确知道转动惯量J的条件下得到的结果，图6-32则考察了转动惯量变化时对转速和负载转矩估计的影响，采用同样的Q和R矩阵。仿真结果表明，转动惯量变化的影响主要体现在转速和负载转矩上，且主要是对动态性能有影响，对磁链观测的影响很小。当转动惯量为实际值的5倍时，图6-32a表明对转速估计在动态过程中出现了一定延迟，图6-32b表明动态过程中负载转矩估计出现了较大误差。根据式（5-3）所示的电机运动方程很容易对上述现象进行解释，转动惯量J只在动态过程中起作用，对于稳态过程没有影响，所以J的变化只影响转速和负载转矩的动态跟踪性能，并不影响稳态时估计精度。

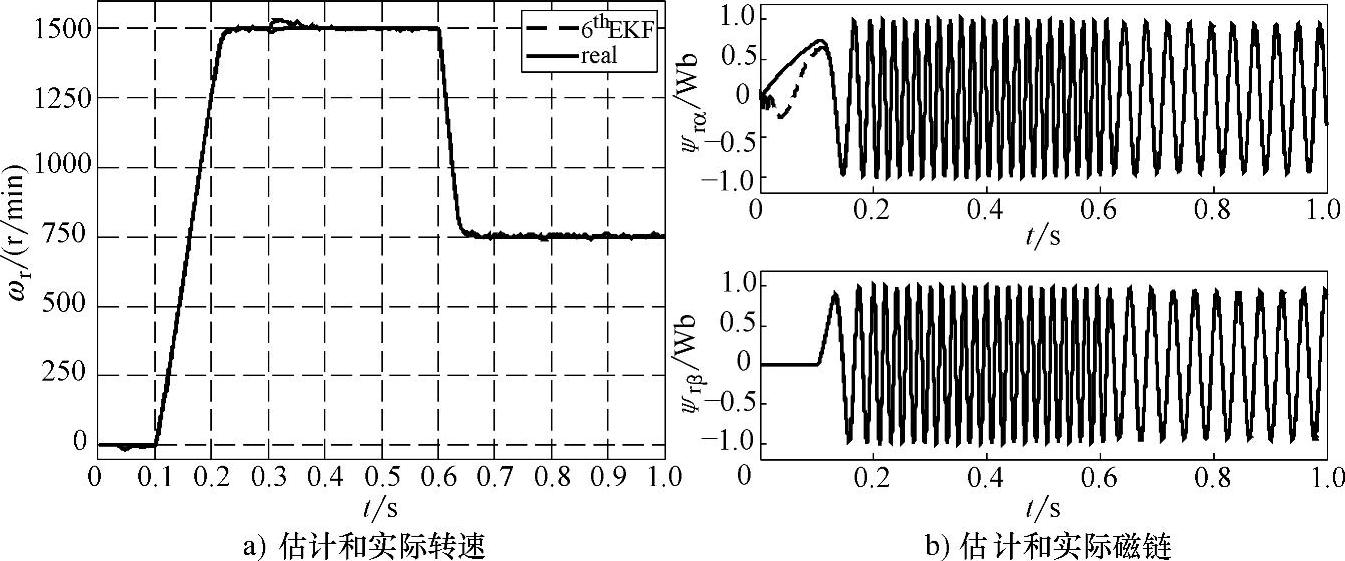
图6-31 6阶EKF仿真结果

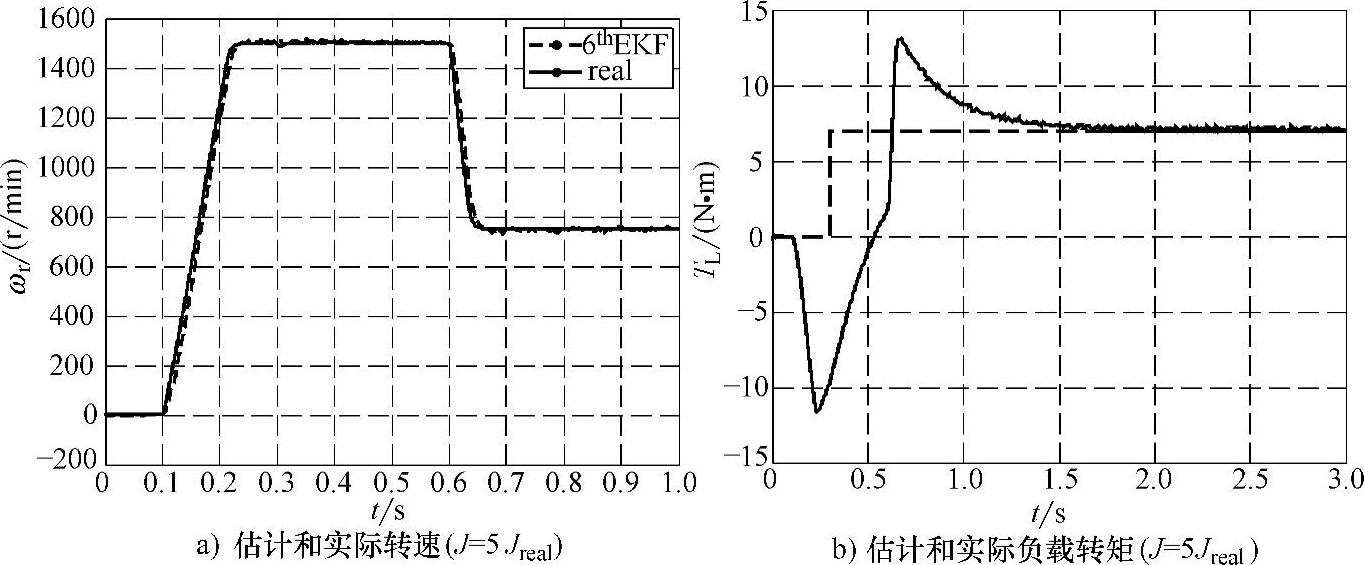
图6-32 转动惯量变化对转速和负载转矩估计的影响