1.滑模控制基本概念

滑模变结构控制与常规控制的不同之处在于它是一个变结构系统，根据系统当时的状态通过改变系统的结构迫使系统响应跟踪预定的轨迹，从而使系统稳定并具有一定的鲁棒性。滑模控制在电机控制中的应用包括滑模控制器和滑模观测器两方面。本节主要研究滑模观测器。

关于滑模控制，首先要介绍一下滑动模态的定义^[9]。对于一般系统来讲，其数学描述为

其状态空间中存在一个切换面s（x）=s（x₁，x₂，…，x_n）=0，将状态空间划分成s＞0和s＜0两部分。在切换面上的点存在三种情况（见图6-23），分别是：

1）通常点——系统运动点到切换面s=0附近时穿越此点而过（点A）。

2）起始点——系统运动点到切换面s=0附近时从切换面的两边离开该点（点B）。

3）终止点——系统运动点到切换面s=0附近时从切换面的两边趋向该点（点C）。

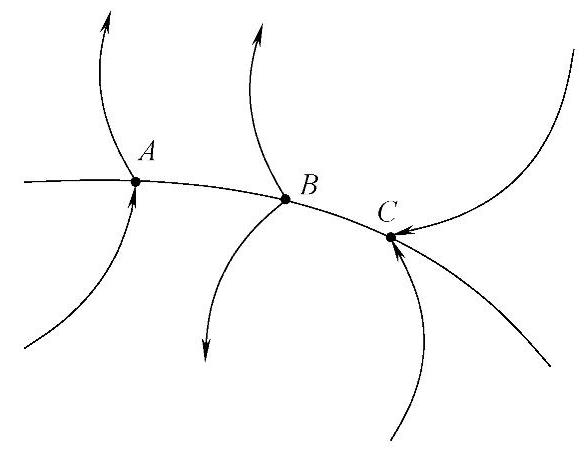
图6-23 切换面上三种点的特性

在滑模变结构控制中，如果在切换面上某一区域内所有的点都是终止点，则一旦运动点趋近于该区域时，就被“吸引”在该区域运动。称在切换面s=0上所有点都是终止点的区域为“滑动模态区”，系统在滑模区中的运动为“滑模运动”。按照滑动模态区上的点都是终止点的要求，可以推出滑动模态存在的条件为

滑模变结构控制的基本问题描述为，对一已知控制系统有

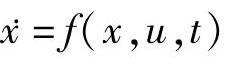x∈Rⁿ，u∈R^m，t∈R

确定一个切换函数

s（x） s∈R^m

求解控制函数

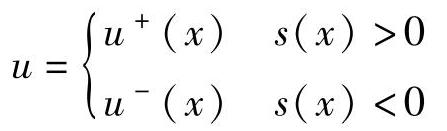
其中，u⁺（x）≠u^-（x），使得

1）滑动模态存在，即式（6-48）成立。

2）满足可达性条件，在切换面s（x）=0以外的运动点都将于有限时间内到达切换面。

3）保证滑模运动的稳定性。

4）满足控制系统的动态品质要求。

上面的前三点是滑模变结构控制的三个基本问题，满足这三个条件的控制才叫滑模变结构控制。如果去掉式（6-48）中的极限条件，则系统状态空间中任何点都将向切换面s=0靠近，同时满足滑模存在和可达性条件，称去掉极限条件的式（6-48）为广义滑模条件，其在实际中应用更加广泛。

2.滑模观测器基本原理

滑模观测器（Sliding Mode Observer，SMO）由于其一系列优点，如在滑模面上的系统降阶、强抗负载干扰能力、实现简单等，在电机控制里得到了广泛研究。本节在前面龙贝格观测器的基础上深入研究了滑模观测器。二者的区别在于反馈项，龙贝格观测器的反馈项是电流误差经过一个连续函数，如式（6-49）所示，而滑模观测器是电流误差经过一个开关函数，如式（6-50）所示。(www.daowen.com)

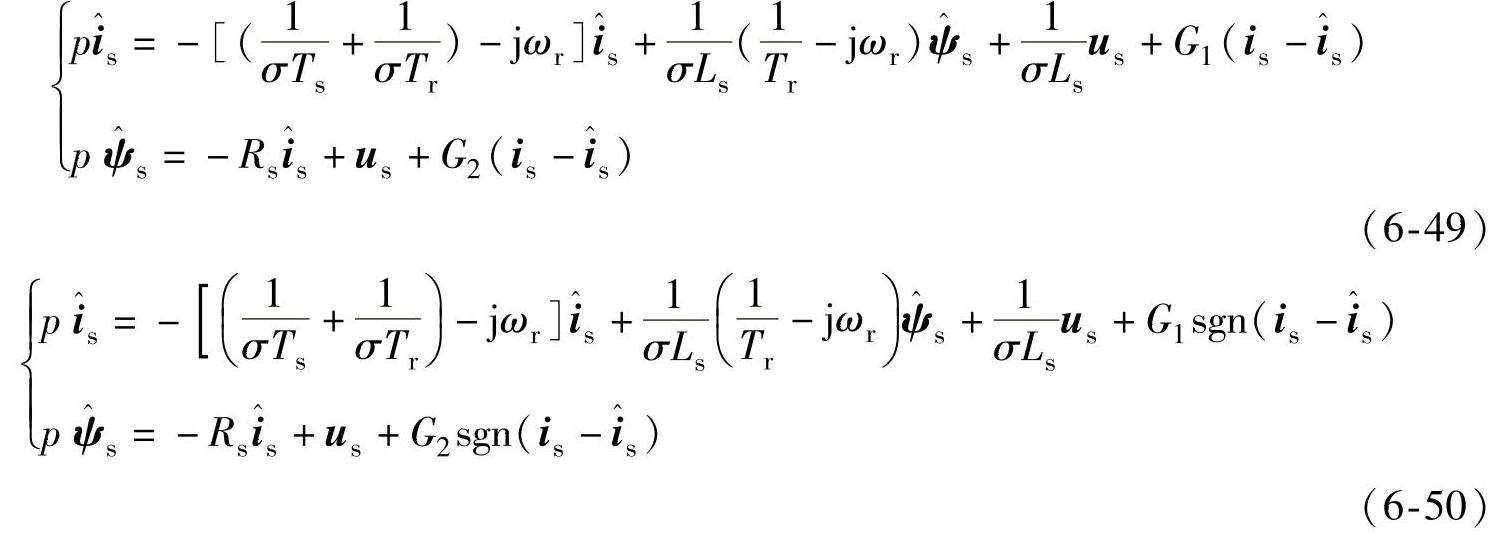
式中 σ=1-L²_m/（L_sL_r），T_s=L_s/R_s，T_r=L_r/R_r。

由于采用了开关函数sgn（），系统的鲁棒性得到增强，但同时也带来一定的噪声，在实际应用时常采用饱和函数sat（）来代替sgn（），如式（6-51）所示，其中Δ表示一个小的正实常数。

滑模观测器式（6-50）的稳定性以及转速自适应律可以应用Lyapunov稳定性定律得到^[9]，类似于式（6-22）～式（6-28）的推导过程，限于篇幅不再详细推导，而直接给出转速辨识结果，即

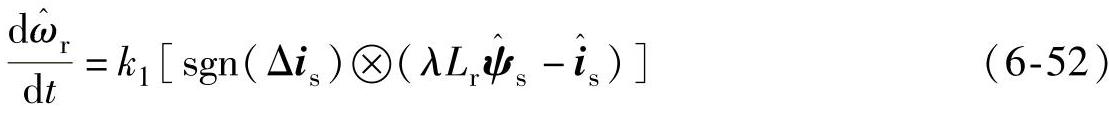
实际应用中为了得到平滑的转速辨识结果，通常需要加一个低通滤波以滤除开关函数带来的高频分量。经过仿真和实验研究发现，式（6-52）中的符号函数如果去掉，即采用和龙贝格观测器一样的自适应率，转速辨识结果更加平滑和准确，因此本节即采用去掉符号函数后的自适应律。

3.滑模观测器增益矩阵研究

增益矩阵设计是观测器研究中的一个重点内容，其关系着观测器的收敛速度乃至系统稳定性。关于滑模观测器，通常采用固定常数的增益矩阵^[10]。它的特点是比较简单，容易实现，但需要对常数进行调试以在系统动态和静态性能上都取得良好的效果。寻求简单易用的增益矩阵是滑模观测器实际应用中需要重点研究的问题。

研究发现，采用和龙贝格观测器一样的增益矩阵可以在实际中取得良好的效果。由于龙贝格观测器研究相对广泛和深入，关于龙贝格观测器增益矩阵的研究成果可以直接应用到滑模观测器中。这里在6.2.1节深入研究龙贝格观测器的基础上，研究比较了两种增益矩阵：一种是式（6-43）所示的含有转速的增益矩阵Ⅰ，在无速度传感器应用中采用估计转速代替实际转速；一种是式（6-44）所示的固定常数增益矩阵Ⅱ。图6-24所示是采用两种不同类型增益矩阵时的转速辨识结果对比，前者比后者更加光滑，但相应的对自适应率中的PI系数更加敏感，这是使用时需要注意的地方。由于二者在动静态性能方面并没有明显的差别，在实际实验中，为了便于实现，采用了固定常数增益矩阵Ⅱ。另外，由于引入了开关函数，与同样的龙贝格观测器相比，鲁棒性有所增强，但同时转速辨识结果也有更多的毛刺，即稳态效果稍微差一些。

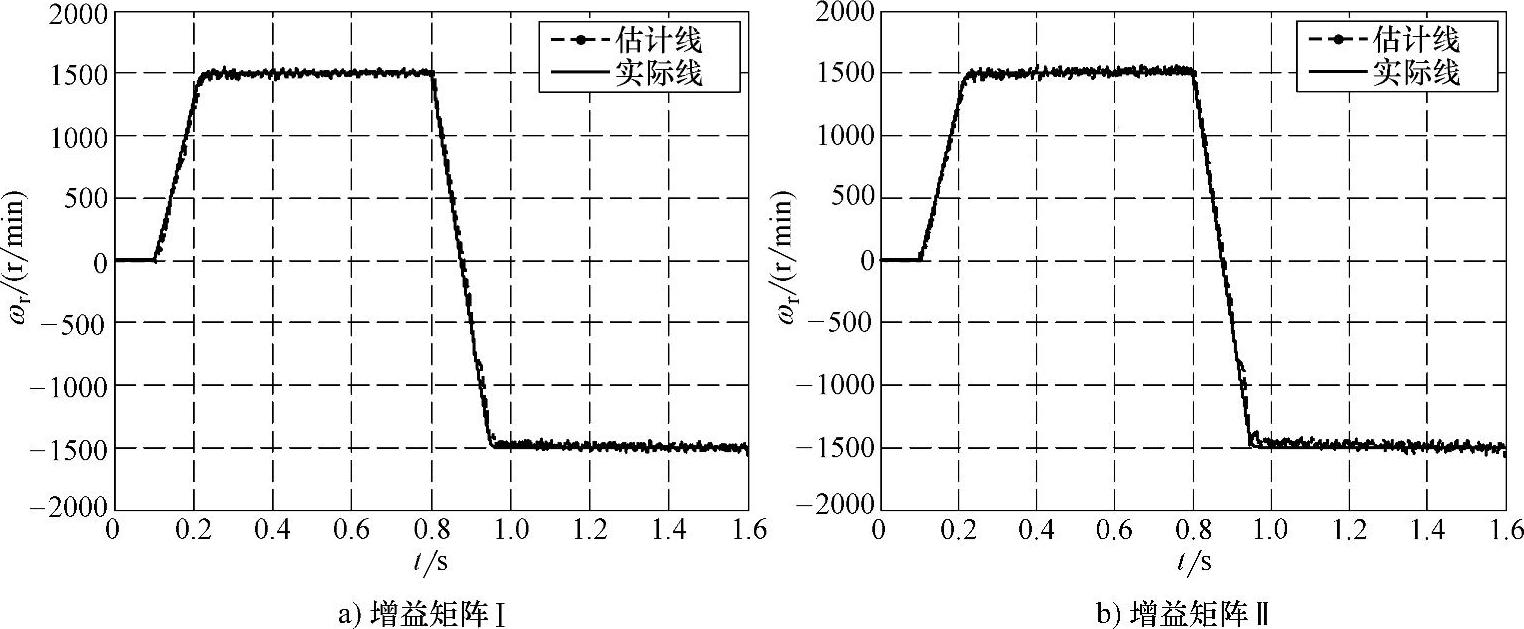
图6-24 转速辨识结果对比

进一步引进式（6-45）、式（6-46）所示的转矩观测器后转速的辨识结果更加平滑准确，如图6-25所示。而且引入转矩观测器后，自适应律中的PI系数整定相对更加容易。

4.观测器的数字化实现

为了便于在DSP等数字控制芯片中实现这里的观测器算法，需要对其进行离散化。常用的离散化方法有前向欧拉法、后向欧拉法和梯形法，前两种离散方法在采样周期T_s比较小时效果差不多，梯形法理论上有更高的精度，但实现相对复杂。在采样率足够高时，采用简单的前向或后向欧拉法一般可以满足需求。参考文献[4]指出在高速时，采用简单的前向欧拉法离散化观测器有可能出现不稳定现象，简单分析可知该稳定区域在复平面上是一个以（-1/T_s，0）为圆心，1/T_s为半径的一个圆^[11]，因此采用简单一阶欧拉法对观测器进行离散化时，其稳定区域主要受制于采样频率T_s。

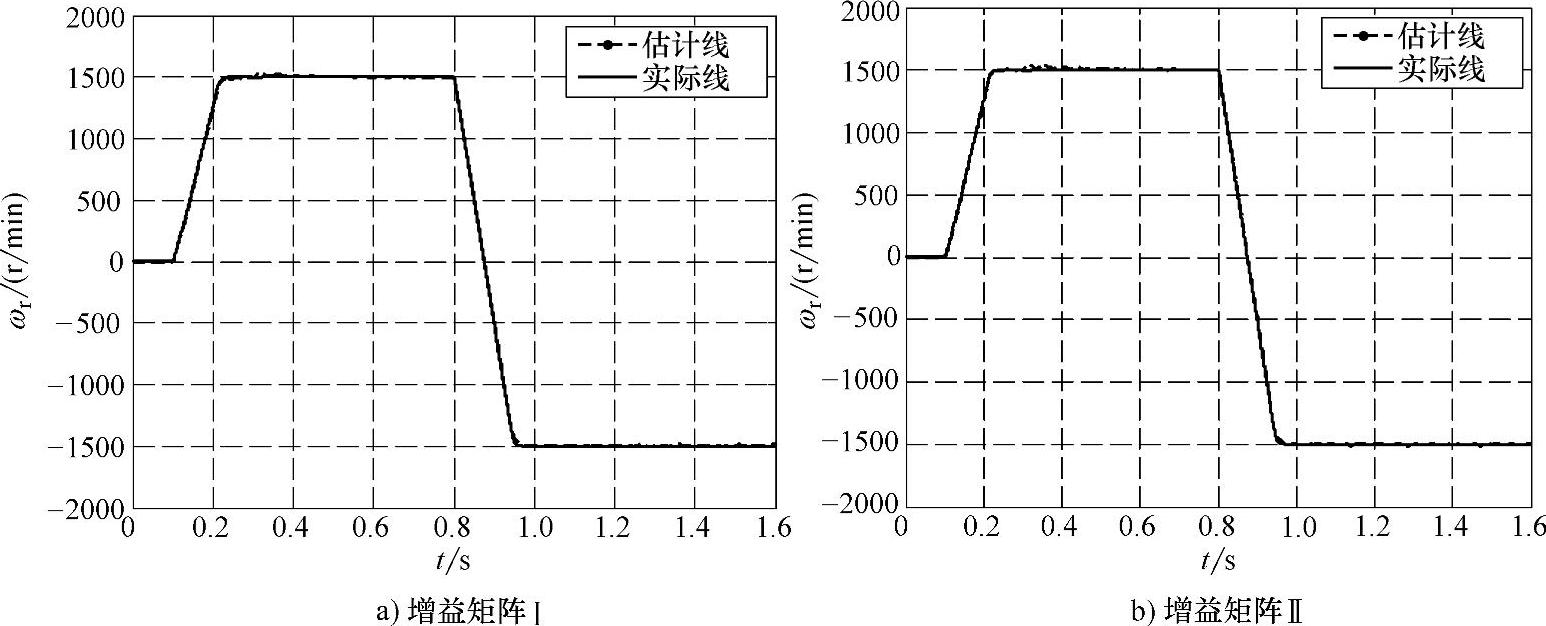
图6-25 引入转矩观测后的转速辨识结果对比

改善观测器离散化实现时在高速的稳定性可以采用式（6-43）和式（6-44）所示的新型增益矩阵。图6-26给出了采用改进增益矩阵[式（6-44），图中G1所示]、采用经典增益矩阵[式（6-20），图中G2所示]两种观测器的极点，以及电机本身的极点分布（图中IM所示），G2虚线代表的是采用前向欧拉法离散时观测器的稳定区域范围。可以看出，在转速高达1.6p.u.时，采用经典增益矩阵的观测器已经超出稳定范围，而采用将电机极点左移的方法则依然可以保持观测器在稳定区域内。

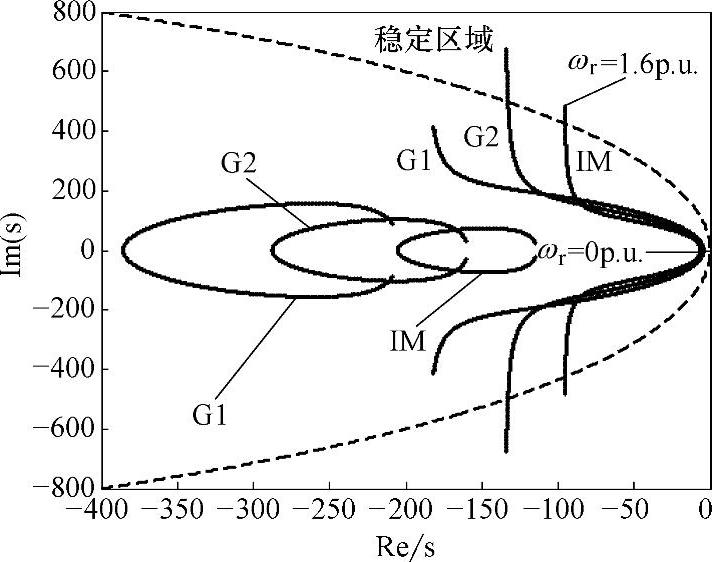
图6-26 电机极点与采用不同增益矩阵时的观测器极点

另外一种改善观测器稳定性的方法是通过改善离散时的积分方法来实现。传统的离散化方法中状态变量的更新需要到下一个采样时刻才更新，尤其具有多个状态变量而且互相之间又有耦合的观测器。在TI的技术文档中采用了基于预测-校正技术的梯形积分法^[12]，可以保证较高的精度，但计算相对复杂，在实时性要求严格的地方不太实用。这里采用了一种新型的积分方法，在某一时刻状态变量得到更新时立刻将其用于计算别的状态变量，而不是采用一阶欧拉法时要到下一个周期才用更新后的状态变量进行计算，这样就减少了延迟，提高了系统的精度。这种方法可以认为是前向欧拉法和后向欧拉法相结合的一种混合积分方法，比梯形法简单，计算量没有增加，但精度得到了提高，是一种性能比较好的积分方法。本节的观测器实现时即采用了这种方法。

5.仿真结果

在MATLAB/Simulink中进行了仿真，电机参数同6.2.1节第5部分。在0.1s前电机进行直流预励磁，等磁通建立起来后，转速指令在0.1s从0r/min阶跃到1500r/min，在0.6s阶跃到750r/min。负载转矩在0.3s时从空载变为50%额定负载。图6-27a和图6-27b分别给出了未引入转矩观测和引入转矩观测后的滑模观测器的转速辨识结果，从上至下依次为估计转速、实际转速和二者之间的误差。可以看出，引入转矩观测后转速估计精度和动态性能有所提高。图6-27c和图6-27d进一步考察了引入转矩观测器后转动惯量变化时对速度估计精度的影响。可以看出，转动惯量变化2倍下估计转速依然可以较好地跟踪实际转速，虽然动态性能有所降低，但对稳态精度影响较小。

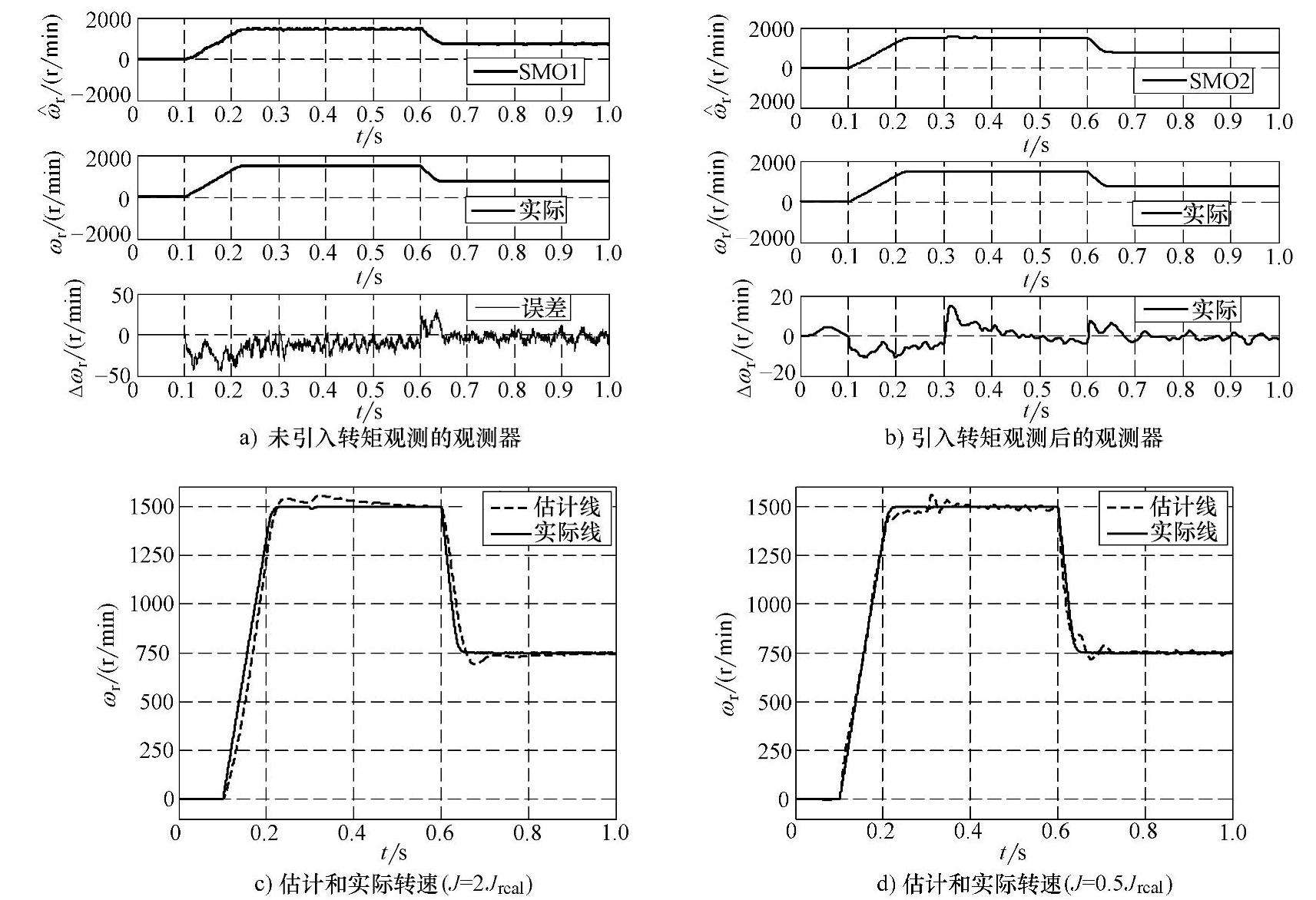
图6-27 0r/min→1500r/min→750r/min仿真波形