1.基本原理
龙贝格观测器(Luenberger Observer,LO)采用了现代控制理论中的状态估计和状态反馈,其特点是利用可测量的输入变量和输出变量来重构不能直接测量的状态,并进行状态反馈,以获得较高的性能。通过配置极点的方法,可以控制系统的动态性能。当观测器的阶数和系统的阶数相同时,称为全阶观测器。
设有以下的n阶线性定常系统:
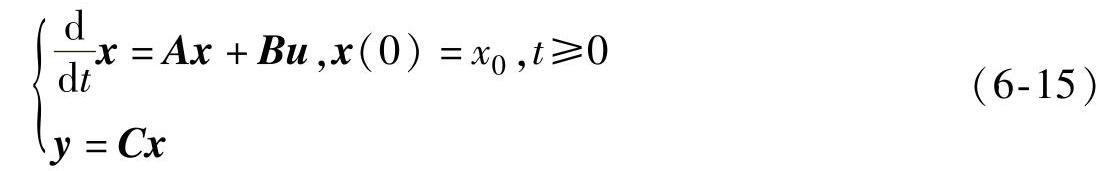
式中 A——系统矩阵,为n×n实常阵;
B——输入矩阵,为n×p实常阵;
C——输出矩阵,为p×p实常阵。
全阶观测器就是以y和u为输入,且其输出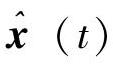 满足
满足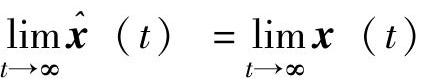 的一个n阶线性定常系统。通常的全阶观测器系统结构框图如图6-19a所示。
的一个n阶线性定常系统。通常的全阶观测器系统结构框图如图6-19a所示。
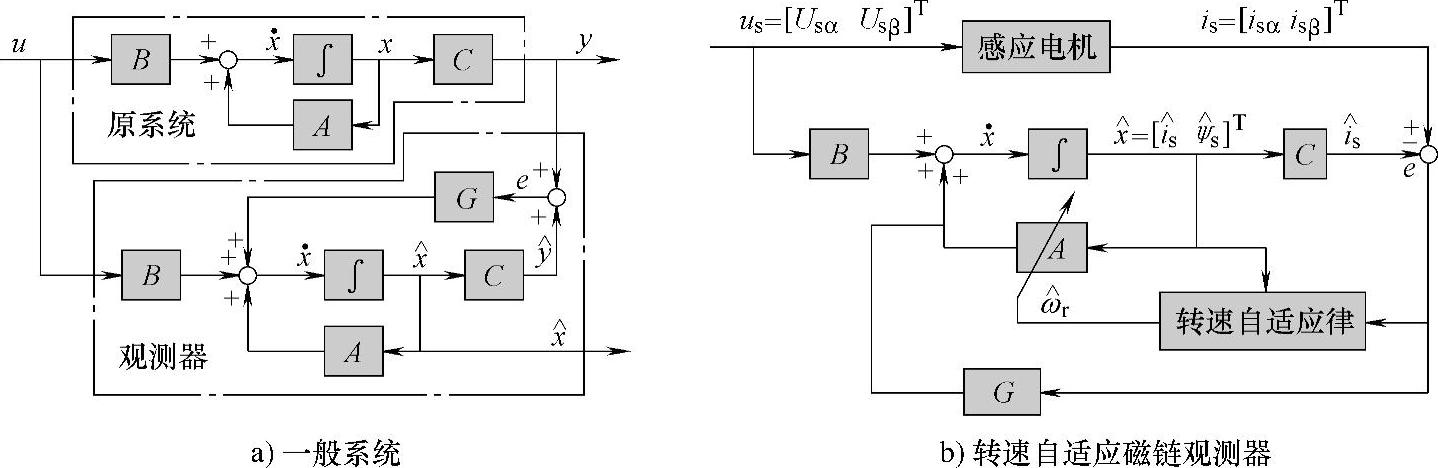
图6-19 全阶观测器系统结构框图
图6-19a中,上面和下面虚线框内分别为原系统和重构系统,取二者输出之差经增益矩阵G后反馈到输入从而构成一个闭环系统,如式(6-16)所示;对于异步电机来说,其转速和磁链观测的全阶观测器框图如图6-19b所示。
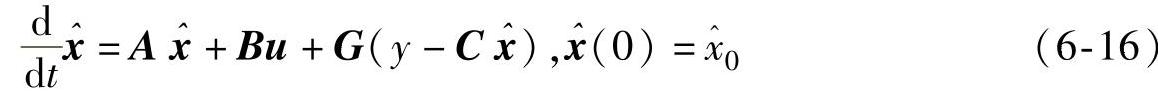
2.不同状态变量下的转速自适应磁链观测器
转速自适应磁链观测器可以以定子电流、定子磁链为状态变量,也可以以定子电流、转子磁链为状态变量,还可以以定子磁链、转子磁链为状态变量。在实际应用中,可以按照实际需求选择不同的状态变量来构造观测器,例如对于转子磁场定向的矢量控制来说,选择定子电流、转子磁链作为状态变量更为合适,因为所需的转子磁链信息可以直接从观测器获取。
(1)定子电流和定子磁链为状态变量的转速自适应磁链观测器
基于龙贝格观测器的方法可以在观测磁链的同时辨识转速,同时可以对部分电机参数进行辨识,是一种性能优良的方法。这里首先以定子电流和定子磁链为状态变量的观测器为例,推导出转速的自适应率和增益矩阵的形式,然后进一步推广到其他状态变量组合的观测器。式(5-5)在静止坐标系下,展开成分量形式的电机方程为

式中
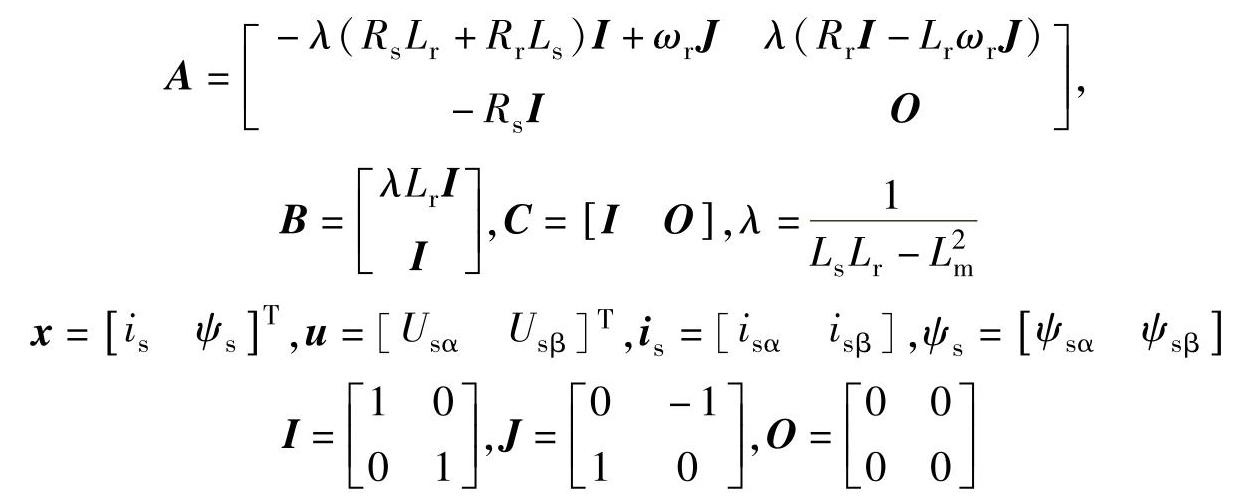
根据式(6-17)可以构造出异步电机的全阶观测器模型为

式中  ,
,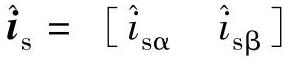 ,
,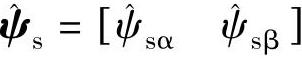 ;
;
G——增益矩阵;
^——表示由观测器估计得到。
增益矩阵G的选择直接关系着观测器的收敛性和稳定性。由于电机是稳定的物理系统,通常选择G使得观测器的极点正比于电机的极点[1-2],并且选择二者极点的比值k>1以保证观测器的稳定性和收敛速度。k越大收敛速度越快,但相应的抗干扰能力下降,因此k值的选择一般是快速性和抗干扰性的折中。增益矩阵G的一般形式为
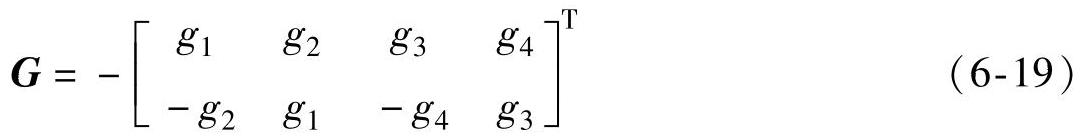
采用参考文献[1]的方法,可以得到矩阵G各个元素的表达式。现有文献通常只给出了一组增益矩阵解[1-2],这里采用解析推导的方法,利用数学软件MAT-LAB推导得出了满足观测器极点和电机极点成正比条件下的六组解[3],其中两组解为
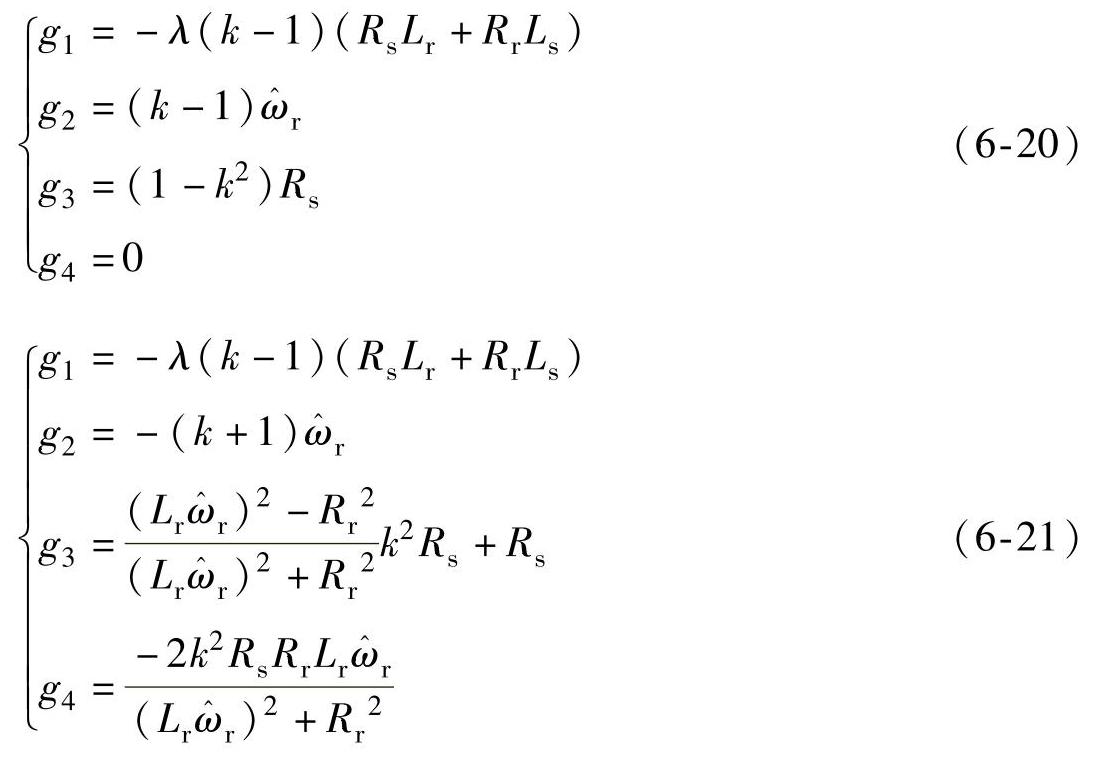
另外四组解由于表达式过于烦琐,这里仅以图形的方式给出六组解G的各个元素随转速变化的曲线,见图6-20。需要说明的是,前四组增益矩阵的各个元素均为实数,第五组和第六组增益矩阵为共轭矩阵,图6-20中对后两组增益矩阵只给出了它们的实部。
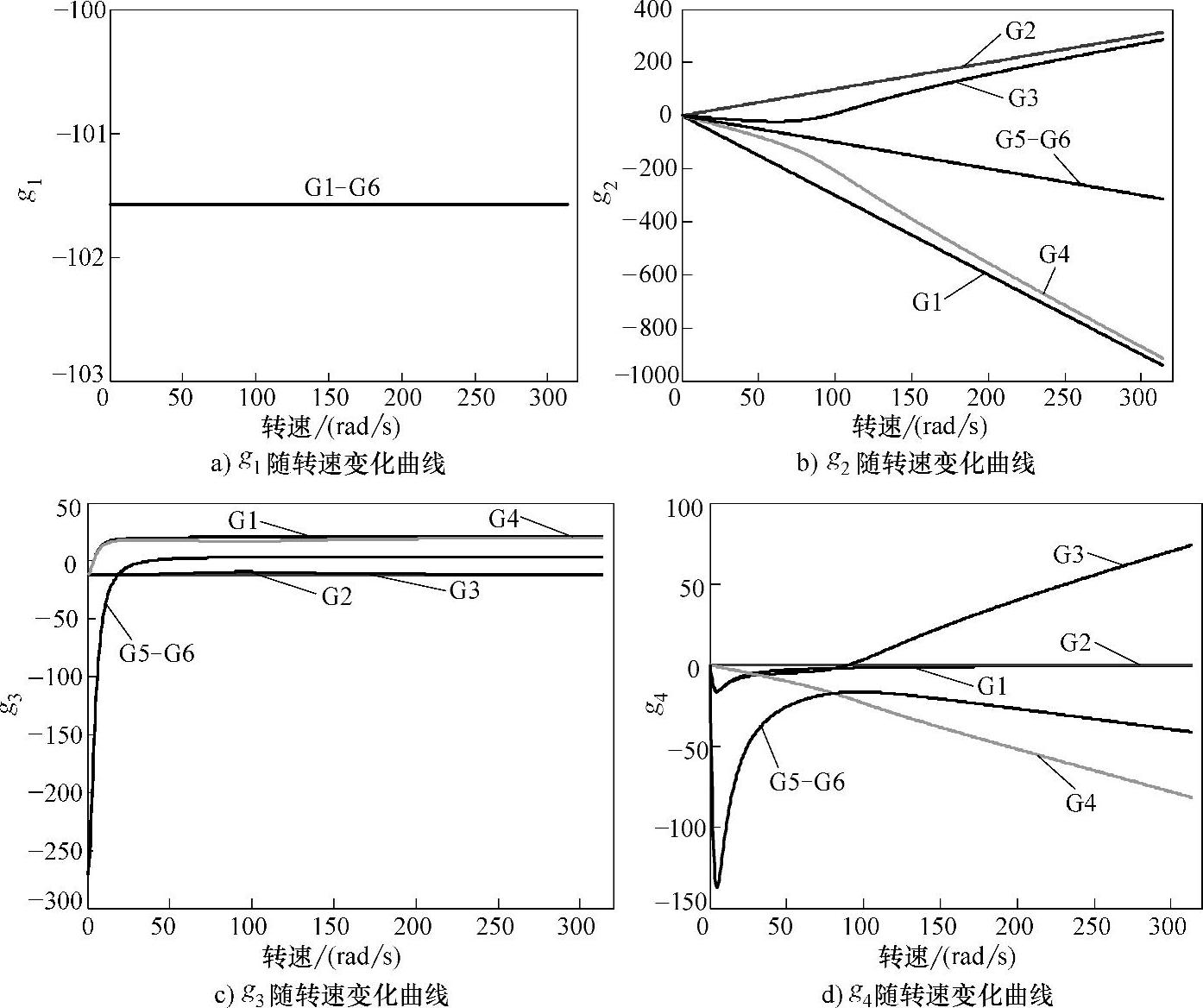
图6-20 以定子电流和定子磁链为状态变量的观测器增益矩阵曲线
(2)转速和电机参数辨识
式(6-18)中含有电机转速和电机定转子参数,电机无速度传感器运行时转速是未知的,运行过程中电机参数由于发热等原因也会发生变化,因此需要对电机转速和参数进行辨识,以保证观测器的稳定运行。以Lyapunov稳定性定律为基础,通过自适应算法可以得出转速和定转子电阻的自适应律,并能保证观测器的收敛性。
假设电机转速和定转子电阻均未知,重写观测器方程式(6-18)为

将式(6-17)减式(6-22)可得

式中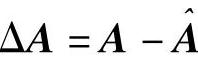 ,
,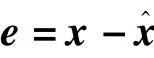 ,记
,记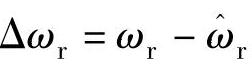 ,
,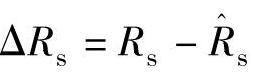 ,
,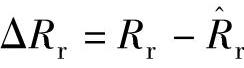 。其中
。其中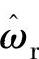 、
、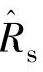 和
和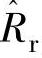 分别为估计的转子转速、定子电阻和转子电阻,有
分别为估计的转子转速、定子电阻和转子电阻,有
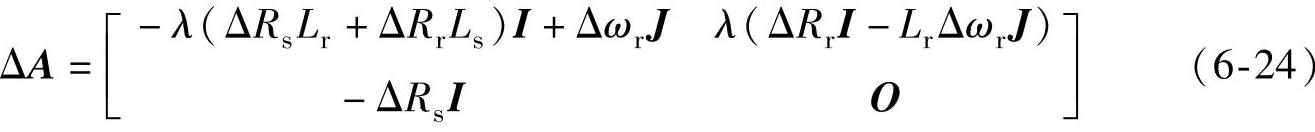
定义Lyapunov函数为
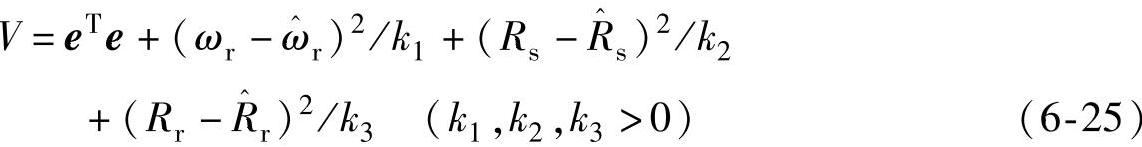
易知V>0,其微分为
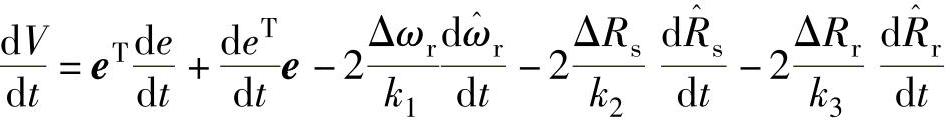
考虑到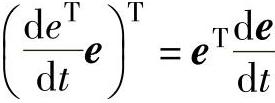 ,有
,有
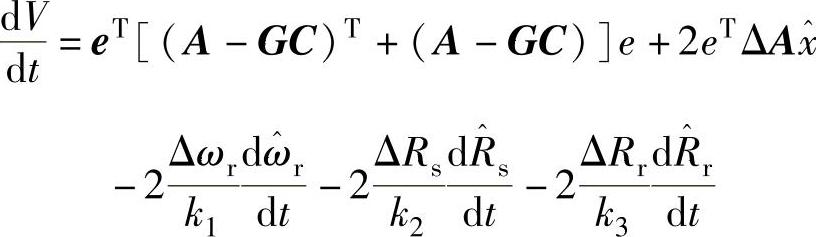
其中
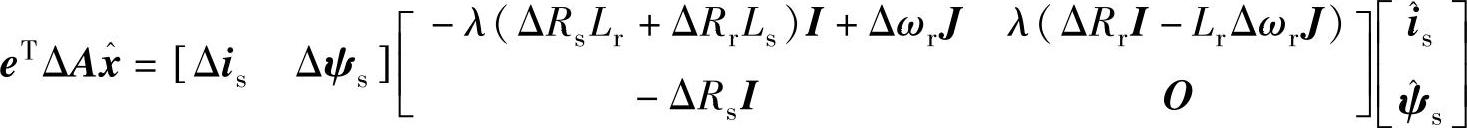 (https://www.daowen.com)
(https://www.daowen.com)
展开并整理最后得到
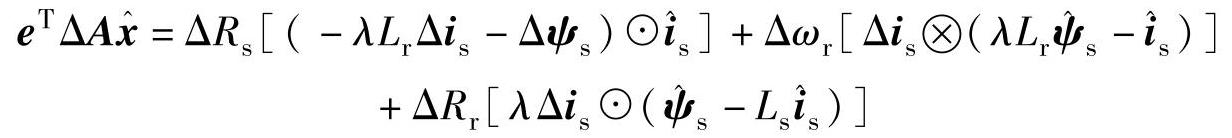
将 代回dV/dt最终得到
代回dV/dt最终得到
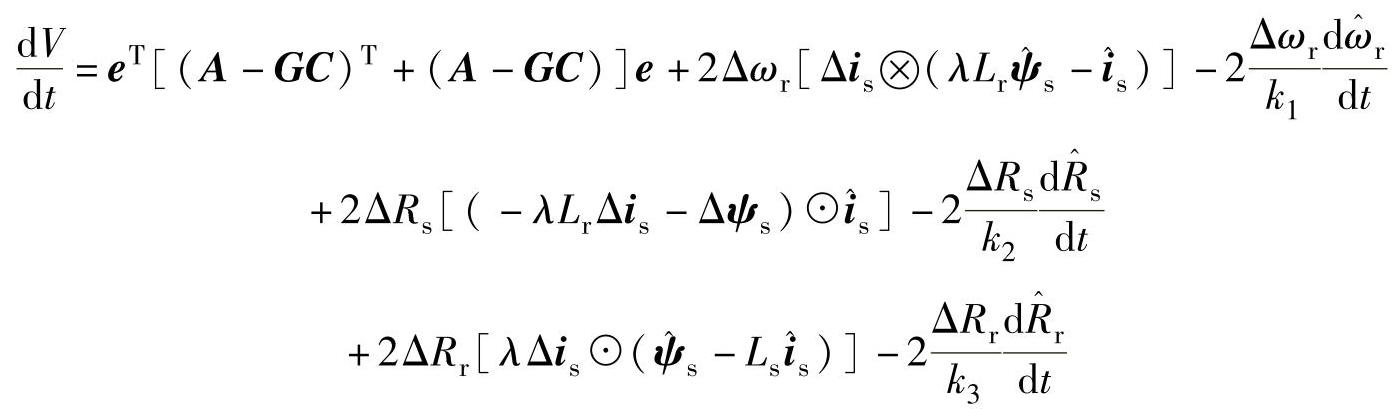
前面G的选择已经保证eT[(A-GC)T+(A-GC)]e为负定矩阵,当满足
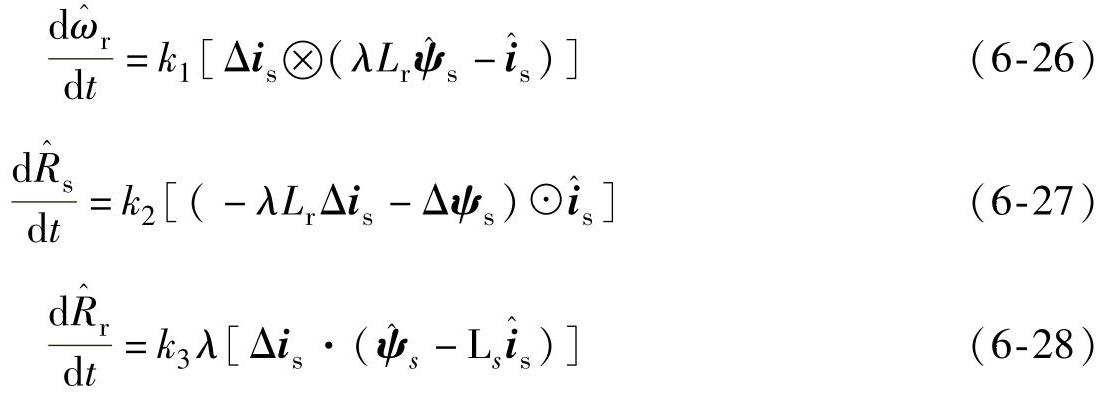
则dV/dt的后六项之和为0,即V>0,dV/dt<0,满足Lyapunov稳定定律。至此,电机转速和定转子电阻的自适应律已经推导得出,如式(6-26)~式(6-28)所示。实际应用中,为了保证实用性和快速性,可以采用PI调节器来代替纯积分。另外,在式(6-27)中由于λLrΔis>>Δψs,且实际系统中Δψs是不可知的,实际应用时通常要忽略掉Δψs,相应的式(6-27)变为

(3)不同状态变量观测器之间的联系和区别
设以定子电流和转子磁链为状态变量的增益矩阵为G1,以定子磁链和转子磁链为状态变量的增益矩阵为G2,它们和以定子电流和定子磁链为状态变量的增益矩阵G的关系可以表达为式
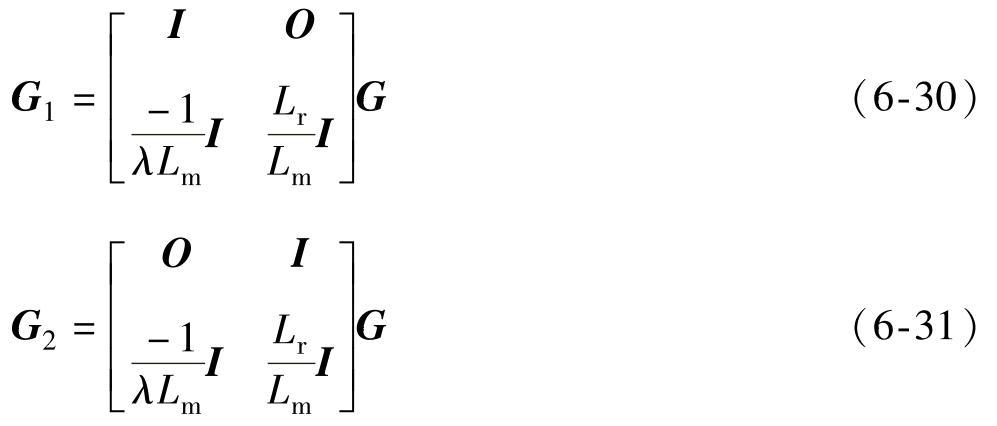
把式(6-20)代入式(6-30)中,可以得到以定子电流和转子磁链为状态变量的观测器增益矩阵各元素表达式如式(6-32)所示,与参考文献[1-2]中给出的一致。
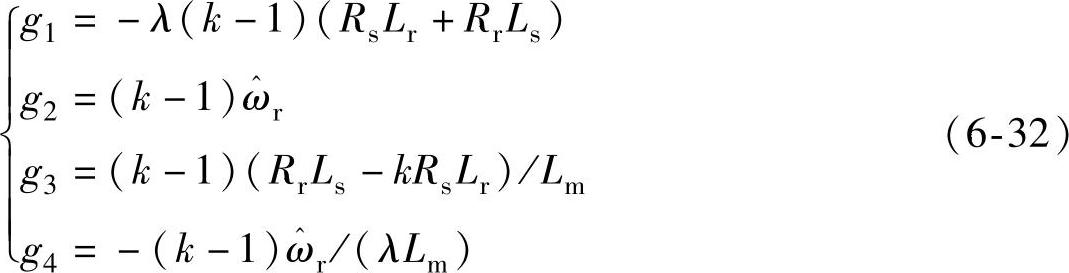
相应的,与式(6-20)对应的以定子磁链和转子磁链为状态变量的观测器增益矩阵各元素表达式为
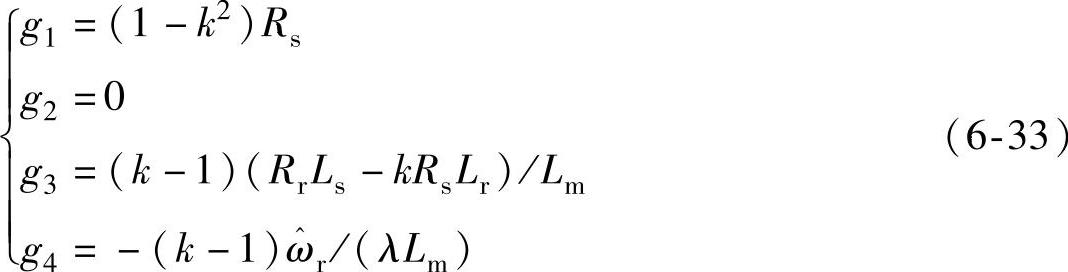
本节采用解析推导的方法共得出了六组增益矩阵,通过代入式(6-30)和式(6-31)可得满足另外两种观测器的六组增益矩阵,其正确性都通过仿真得到了证实。另外,这里是以选择定子电流和定子磁通为状态变量举例进行了推导,但结论适用于另外两种观测器。通常在矢量控制中选择的是以定子电流和转子磁链为状态变量,但由于定子磁链和转子磁链之间可以互相转化,在电机参数准确的情况下,知道了其中的一个,通过定子电流和部分电机参数就可以得到另一个量,见式(6-34)和式(6-35),其中ψr为转子磁链矢量。

比较式(6-26)和式(6-34),可以将式(6-26)写成

式(6-36)与参考文献[1-2]中给出的转速自适应律表达式完全一致,说明状态变量的选择并不影响到最后自适应律本质上的一致性。下面总结了采用其他状态变量时的转速、定子电阻和转子电阻的辨识结果。推导过程与前面类似,为了方便,可以利用MATLAB中的符号工具箱来进行符号推导,以简化过程。需要指出的是:①这里的结果都在静止坐标系下得到;②转子转速和转子电阻在稳态时不能同时辨识,原因是稳态时二者耦合在一起无法分离,从定子侧的电压电流信息只能推出转子电阻和转差的比值,而无法单独得到转子电阻和转差。
(1)以定子电流和转子磁链为状态变量
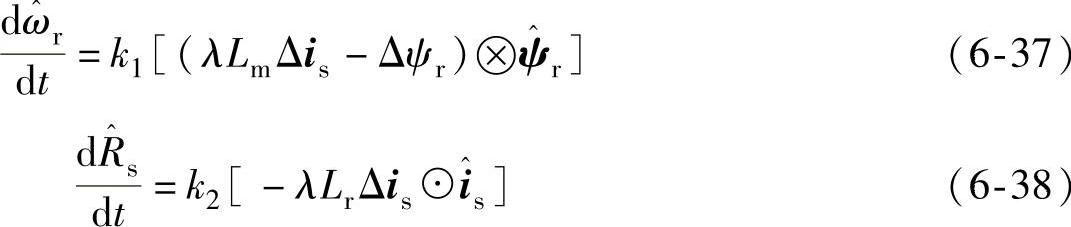
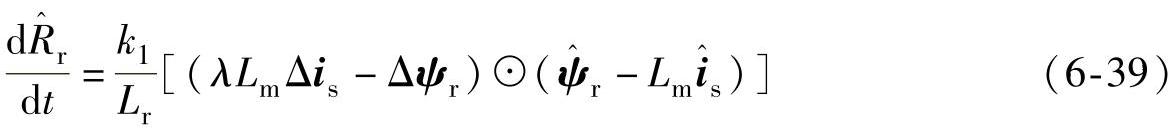
(2)以定子磁链和转子磁链为状态变量
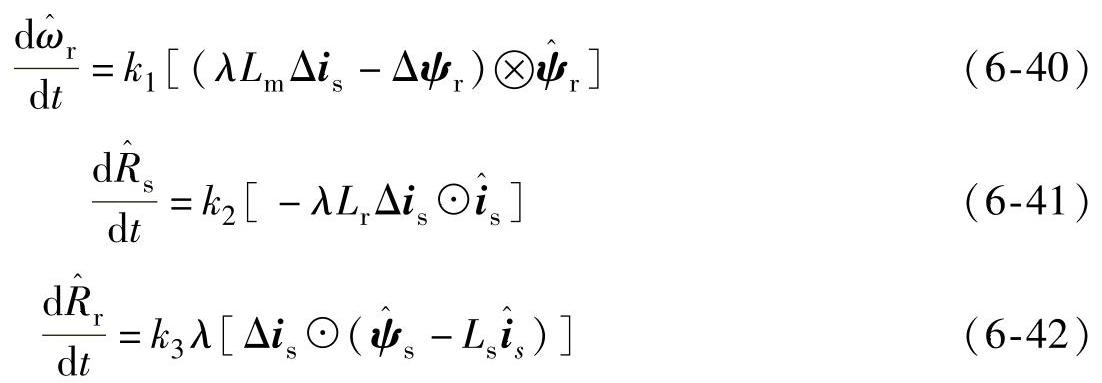
3.新型增益矩阵
图6-20中的增益矩阵采用观测器极点和电机极点成正比的经典极点配置方法,且通常选择比例系数大于1。这种方法的缺点是高速时观测器具有较大的极点虚部,从而可能导致观测器的不稳定。参考文献[4]在以电机转速旋转的坐标系上选择定子磁链和转子磁链为状态变量,将观测器的极点相对于电机极点左移一个常数距离,不改变极点的虚部,系统的稳定性得到了提高,但得到的增益矩阵表达式比较复杂,而且含有估计转速,在实现中采用了高性能浮点DSP,提高了系统成本。另外,参考文献[1-6]给出的增益矩阵中通常含有估计转速,因此不可避免地受到转速估计误差的影响。由于观测器通常采用静止坐标系,这里在借鉴参考文献[4]方法的基础上,在静止坐标系下推导得出了观测器极点相对电机极点左移条件下的新型增益矩阵,并进行了简化,使其表达式中只含有常数,降低了转速估计误差对观测器的影响。
依然以采用定子电流和定子磁链为状态变量的观测器为例,保持观测器极点POb的虚部不变,而将实部在复平面上向相对于电机极点PIM向左平移,即POb=PIM+b(b<0),在静止坐标系下推导得出增益的表达式为
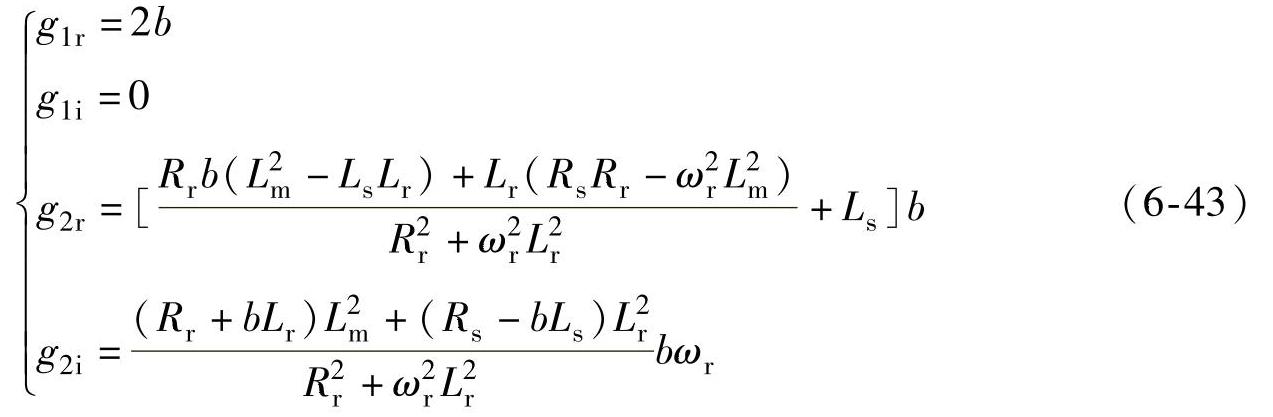
式(6-43)含有估计转速,在计算中要实时更新,而且表达式比较复杂,增加了实现的难度。这里提出了一种简化增益矩阵,即令式(6-43)中ωr=∞,相应的增益矩阵变为常数,因而简化了计算,有利于实时实现,即

图6-21给出了POb=kPIM和POb=PIM+b(ωr=∞)两种情况下的电机和观测器极点的对比。其中,k=1.4,b=-40。图6-21a中的观测器极点在转速较高时有较大的虚部,可能导致观测器不稳定,且增益中包含转速;图6-22b中的观测器极点相对电机极点向左移动,高速时虚部较小,系统稳定性提高,而且计算简单,容易实现。
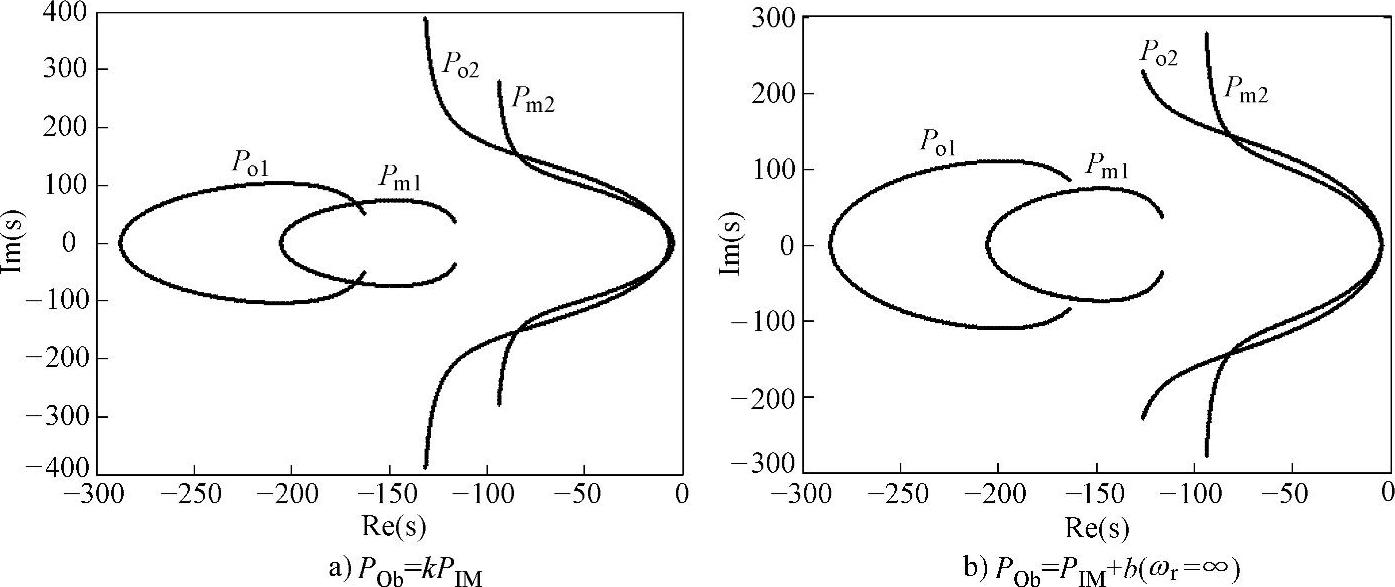
图6-21 不同增益矩阵下的电机和观测器极点
4.引入转矩观测的速度辨识
利用Lyapunov定律可以推导得出转子转速和定子电阻的自适应律,如式(6-26)~式(6-28)。实际应用中为了提高动态响应速度,采用PI来代替式(6-26)~式(6-28)中的纯积分。引入转矩观测的速度辨识可以用式(6-45)和式(6-46)来表示。与式(6-26)相比,增加了机械运动方程以加快转速估计的动态响应[4,7]。
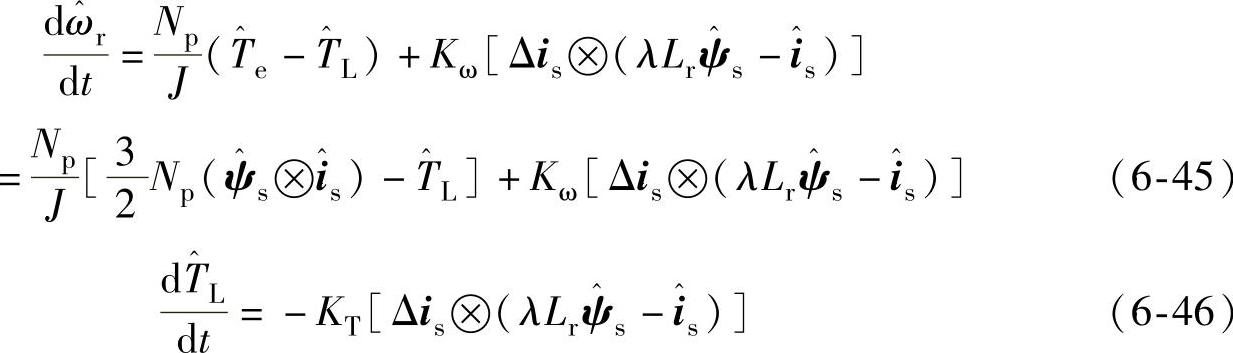
式中 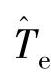 ——观测电磁转矩;
——观测电磁转矩;
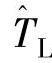 ——负载转矩;
——负载转矩;
Kω,KT——正常数。
式(6-45)和式(6-26)相比,引入了电机运动方程,可以加快转速估计的动态响应。传统的观测器由式(6-17)和式(6-26)组成,引入转矩观测后的改进型观测器由式(6-17)、式(6-45)和式(6-46)组成。
5.仿真结果
为了验证本节所提方法的有效性,在MATLAB/Simulink中进行了仿真。开关频率为5kHz,直流母线电压为560V,电机参数为:2.2kW,2对极,380V/50Hz,定子电阻为2.8452Ω,转子电阻为2.4129Ω,互感为0.2687H,定子漏感和转子漏感均为12.8mH,转动惯量为0.01kg·m2。仿真条件是首先在静止条件下对电机进行直流预励磁,在0.1s时施加一阶跃指令值为1500r/min,此时磁通已经基本建立,电机以最大转矩进行加速直到给定值。0.3s时施加50%额定转矩负载,在0.8s时转速指令值突变为-1500r/min,电机迅速反转直到给定值。图6-22a和图6-22b分别给出了传统观测器和引入转矩后的观测器对转速的估计,可以看出后者观测出来的转速更加平滑,精度更高,延迟更小,具有更好的动静态性能。图6-22c所示是相应的实际负载转矩和估测负载转矩,可见引入转矩观测的观测器可以很快估计出负载转矩。
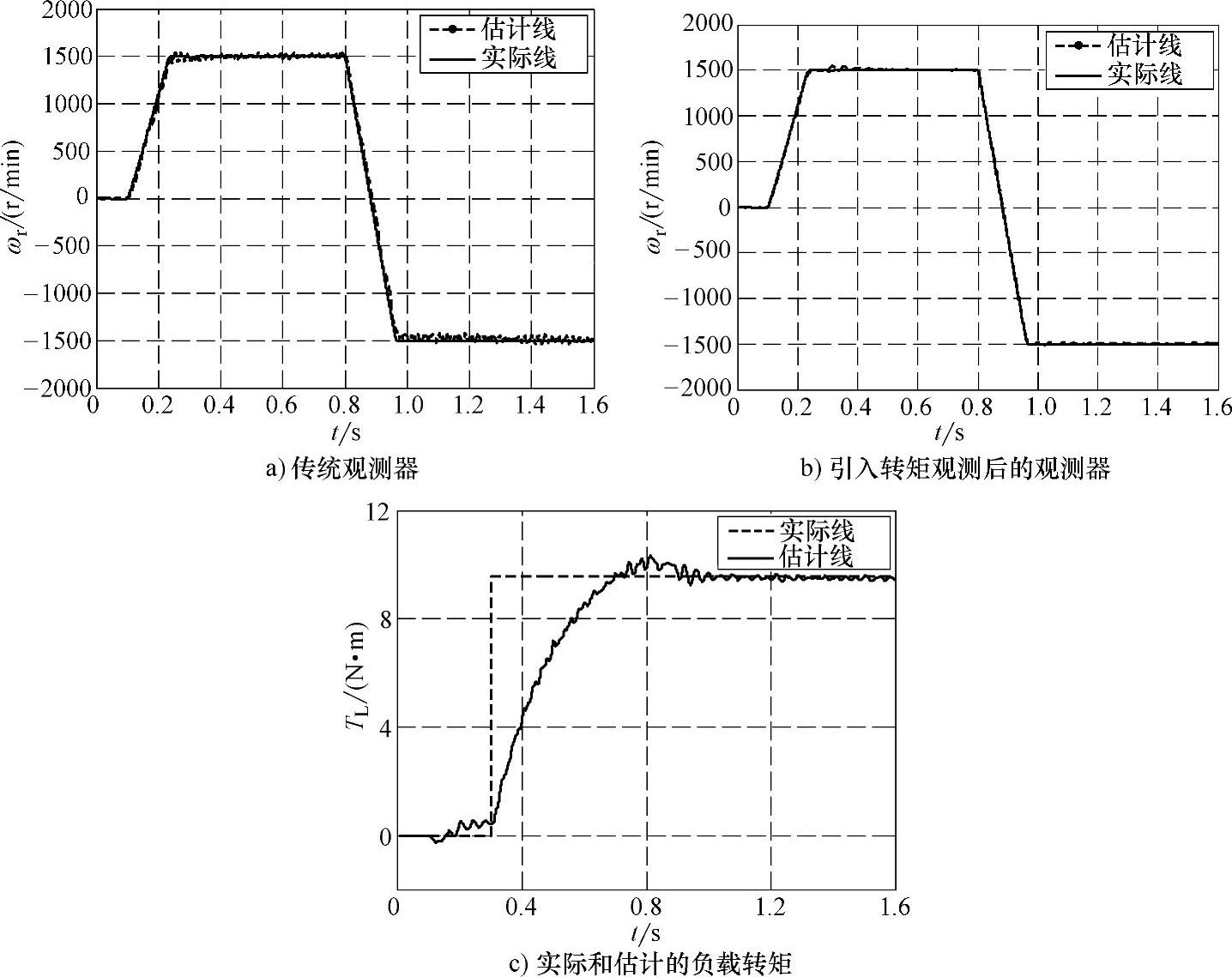
图6-22 0→1500r/min(采用新型增益矩阵)的仿真波形
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






