模糊控制是基于1973年由Zadeh提出的模糊理论的一种智能控制方法，并且由Mandani E H于1974年首次成功用于蒸汽机的自动控制中^[5]。模糊控制以人的经验和知识为基础，不需要精确的数学模型和参数，对参数变化的线性或非线性对象具有很强的鲁棒性。智能控制除了模糊控制外，还包括专家系统和神经网络，而模糊控制作为智能控制中最成熟的方法，已经得到了广泛研究和关注，并且被应用到电机传动中^[14-17]。

实际控制系统中，由于控制过程或被控对象的复杂性，往往有很多难以精确量化的模糊量，采用传统方法难以得到很好的控制。而这些复杂的系统由人根据经验和知识进行模糊推理、判断，却往往控制得很好。模糊控制正是利用了人的经验和知识，并且采用模糊逻辑语言来对真实世界的不确定性和近似性进行刻画。它摒弃了二值逻辑简单的肯定或否定，允许一个命题亦此亦彼，存在着部分肯定和部分否定，只不过隶属程度不同而已。

模糊控制与常规控制相比，具有如下特点：

1）对控制对象的数学模型和参数依赖性小，是在操作人员的控制经验基础上实现对系统的控制。

2）是一种灵活的非线性控制器，可以处理复杂的非线性系统。

3）鲁棒性强。对控制对象参数的变化不敏感，适用于线性或非线性、时变、时滞系统的控制。

模糊控制的特点使得它十分适合用来处理如异步电机这种模型确定、参数变化以及负载干扰不定的系统。

1.模糊控制基本原理

一个典型的模糊控制框图如图5-21所示。它包括模糊控制器和控制对象，其中r（t）是给定输入，u（t）是控制对象的输入，y（t）是控制对象的输出。虚线框内表示一个模糊控制器，它包括模糊化、模糊推理、模糊规则和解模糊几个部分，模糊控制器的输入为误差e和误差变化率de/dt，输出为控制增量du，积分后得到实际控制量u。K_e和K_ce分别是模糊化的输入定标因子，K_u是输出定标因子，E和CE是模糊化后的模糊变量，DU是模糊输出控制变化量。

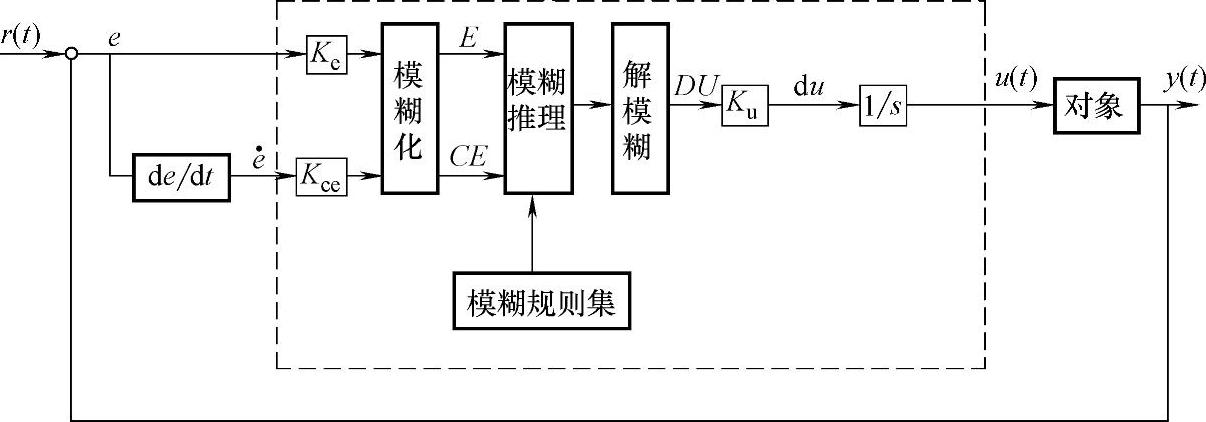
图5-21 典型模糊控制框图

一个模糊控制器的设计包括如下几部分主要内容：

1）选择输入、输出变量。目前广泛应用的是二维模糊控制器，即输入为误差和误差的变化率，输出为控制量的变化。理论上讲，模糊控制器的维数越高，控制越精细，但维数越高导致规则也越多，控制算法也越难以实现。

2）输入变量的模糊化。模糊化是通过输入隶属函数来实现把某一论域映射到[0，1]范围内。隶属函数有多种，如三角形函数、梯形函数和高斯函数等。这里选择的是三角形函数。

3）模糊规则。模糊规则类似操作人员的手动控制策略，它是一系列的模糊条件语句，通常写成if条件then结论的形式。通过总结人在长期生产实践中的经验，运用模糊集合理论和语言变量的概念，可以把利用语言归纳的手动控制策略用计算机程序来实现，这样就可以达到计算机来代替人工作的目的。选取控制量变化的原则是：当误差较大时，选择较大的控制量以尽快消除误差为主；当误差较小时，选择控制量要尽快减少超调，以系统的稳定性为主要指标。

确定模糊规则可以通过四种方法获得：①专家经验法——此种方法主观性比较强；②观察法——由操作员的经验累积来决定；③模型法——根据受控系统的特性来确定；④自组织法——此种方法能够随着环境的变化或经验的丰富更新原有的控制规则以获得更佳的控制效果。

4）模糊推理。模糊推理就是根据模糊规则，以条件到结论为基础去计算模糊子集中的隶属度，然后产生那些将要被执行的动作的过程。它包括两步，首先是对规则的条件部分进行推理，然后是对规则的结论部分进行推理。这里采用的推理方法是Mamdani的Min-Max法。

5）解模糊。模糊控制器的输出依然是模糊变量，必须将它转换为可直接作用于被控对象的清晰变量，这种将模糊值转化为清晰值的过程称为解模糊，也叫反模糊或去模糊。常用的有三种方法：最大隶属度函数法、重心法和加权平均法。本节采用的是重心法。(www.daowen.com)

2.模糊速度和磁链控制

以速度模糊控制器为例进行说明。输入和输出变量定标后的论域范围为[-1.4，1.4]。本节的输入和输出定标因子分别为K_e=1.0，K_ce=120，K_u=600。输入变量模糊化语言值选为7个：正大（PB）、正中（PM）、正小（PS）、零（Z）、负小（NS）、负中（NM）和负大（NB）。输出由于在原点（稳态点）附近要求信号更加精确，采用9个模糊语言值描述，与输入相比，增加了正正大（PVB）和负负大（NVB）。为简化计算，隶属度函数按三角形分布，且取为非对称的不规则三角形，当控制器输入变化量大时输出变化量也大，而在误差较小时输出也小，即在零附近调节更加精细，有利于系统稳定和提高静态性能。图5-22a和图5-22b所示是输入隶属函数分布，图5-22c所示是输出隶属函数分布，图5-22d所示是模糊控制器的输出曲面。

模糊规则库是模糊推理的核心，本节采用的模糊控制规则见表5-1。采用Mamdani型模糊推理算法，模糊推理合成规则为“极大-极小”合成规则，最后的解模糊采用重心法得到输出。将上述模糊控制器用到转速和磁链控制中，转速FLC的输入为给定转速和估计转速的误差，输出为转矩电流。磁链FLC的输入为给定磁链和估计磁链的误差，输出为励磁电流。为简单起见，二者采用同一个FLC，仅输入定标系数和输出定标系数不同。

表5-1 模糊控制规则

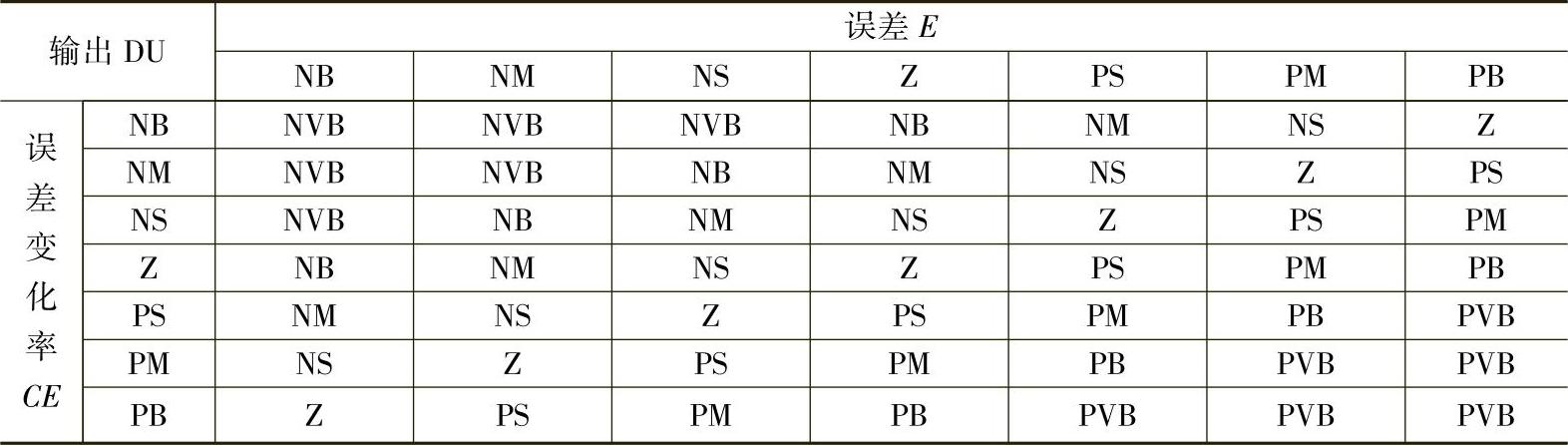
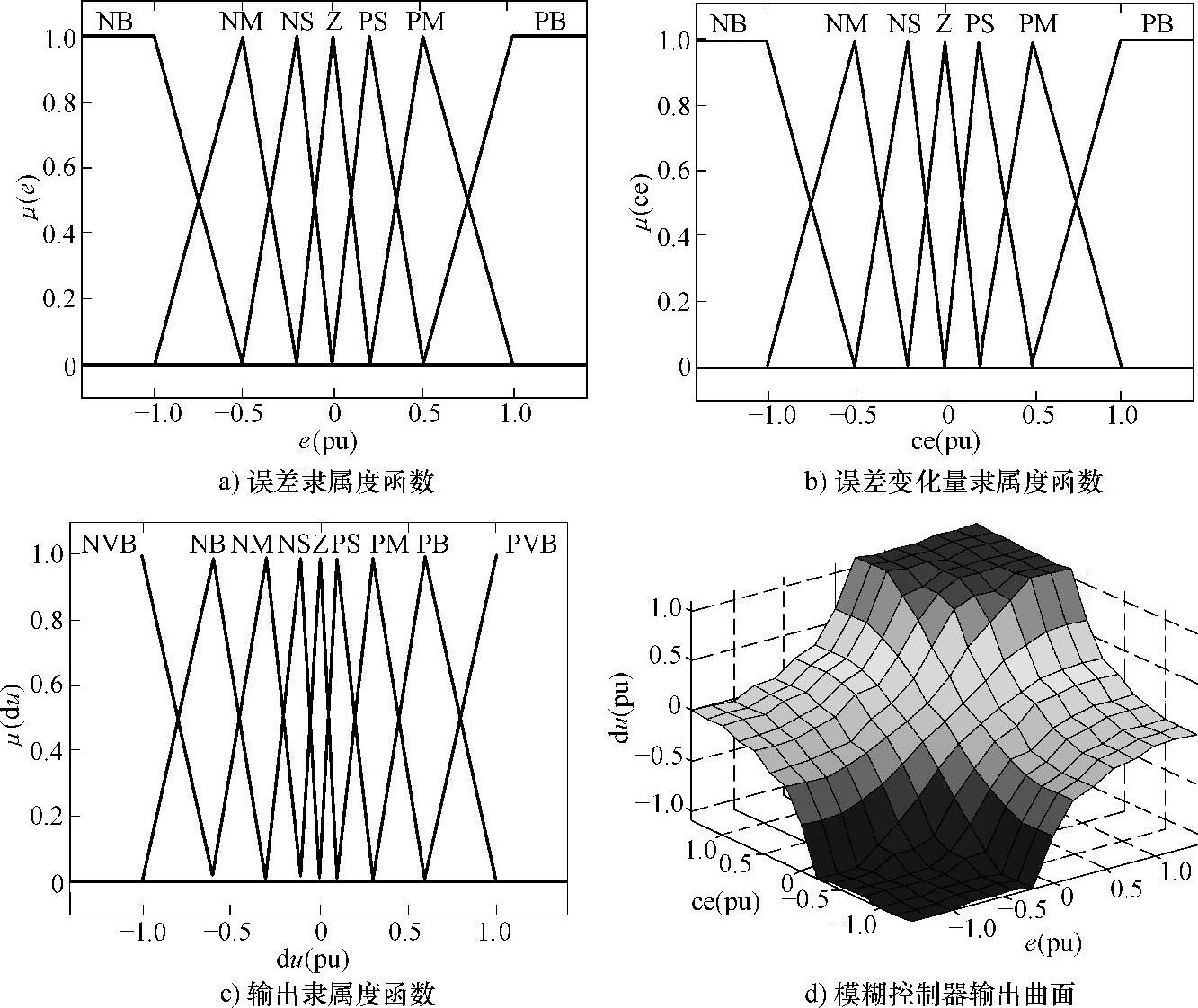
图5-22 模糊速度控制器隶属度函数和输出曲面

在DSP实现时，为了减少计算量，采用二维插值查表的方法实现。也就是先离线计算把图5-22d所示的模糊控制曲面以表格的形式存到DSP中，在实时计算时再查表输出。为了不显著增加存储量同时又不丧失输出精度，采用了二维线性插值的方法来计算输出。

二维线性插值具体说明如下：设某一点（x，y）满足x_i＜x＜x_i+1，y_j＜y＜y_j+1，在点（x_m，y_n）处的值为z_m，n，其中（m=i，i+1，n=j，j+1）。假设点（x，y）对应的输出为z，则有

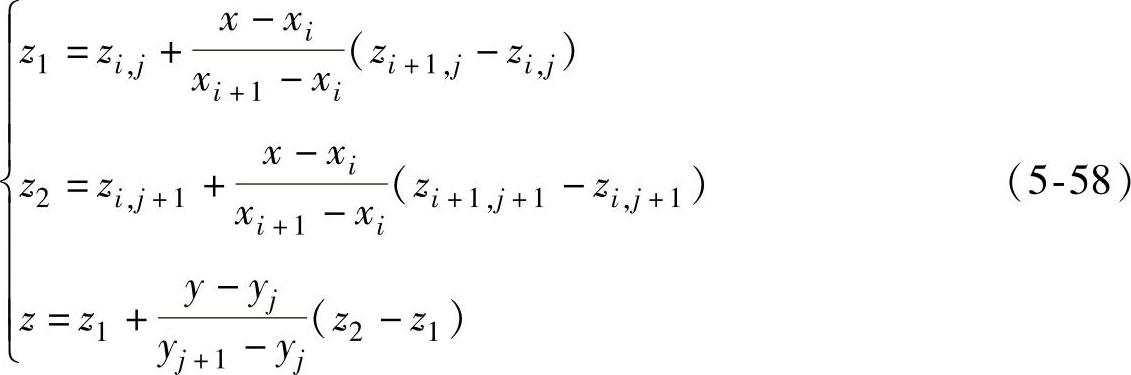
3.模糊电流控制

模糊控制器也可以用于电流控制中，由于模糊控制的强鲁棒性以及处理非线性系统的能力，在电流控制中甚至可以省掉解耦项而系统依然可以具有良好的动态性能^[14]。电流控制器可以采用和速度模糊控制器同样的结构，这样只需要改变输入、输出定标系数，简化了系统结构。

4.仿真结果

仿真条件同前面的滑模控制，考虑到实际实现中FLC计算量较大且需要一定存储空间，从节约资源和提高实时性的角度，这里仅在转速和磁链环采用了结构相同而系数不同的模糊控制，内部电流环依然采用传统的PI电流加前馈解耦。图5-23所示是采用模糊控制时的仿真波形。从图5-23a和图5-23b可以看出模糊控制具有很好的稳态性能，没有稳态误差，动态响应也十分迅速，仅在突加突减负载时转速略有波动，而且很快恢复到稳态，证明了模糊控制对外加干扰的强鲁棒性；从图5-23c和图5-23d可以看出电流响应十分迅速，而且与滑模控制相比波形更加平滑，具有更好的稳态性能。

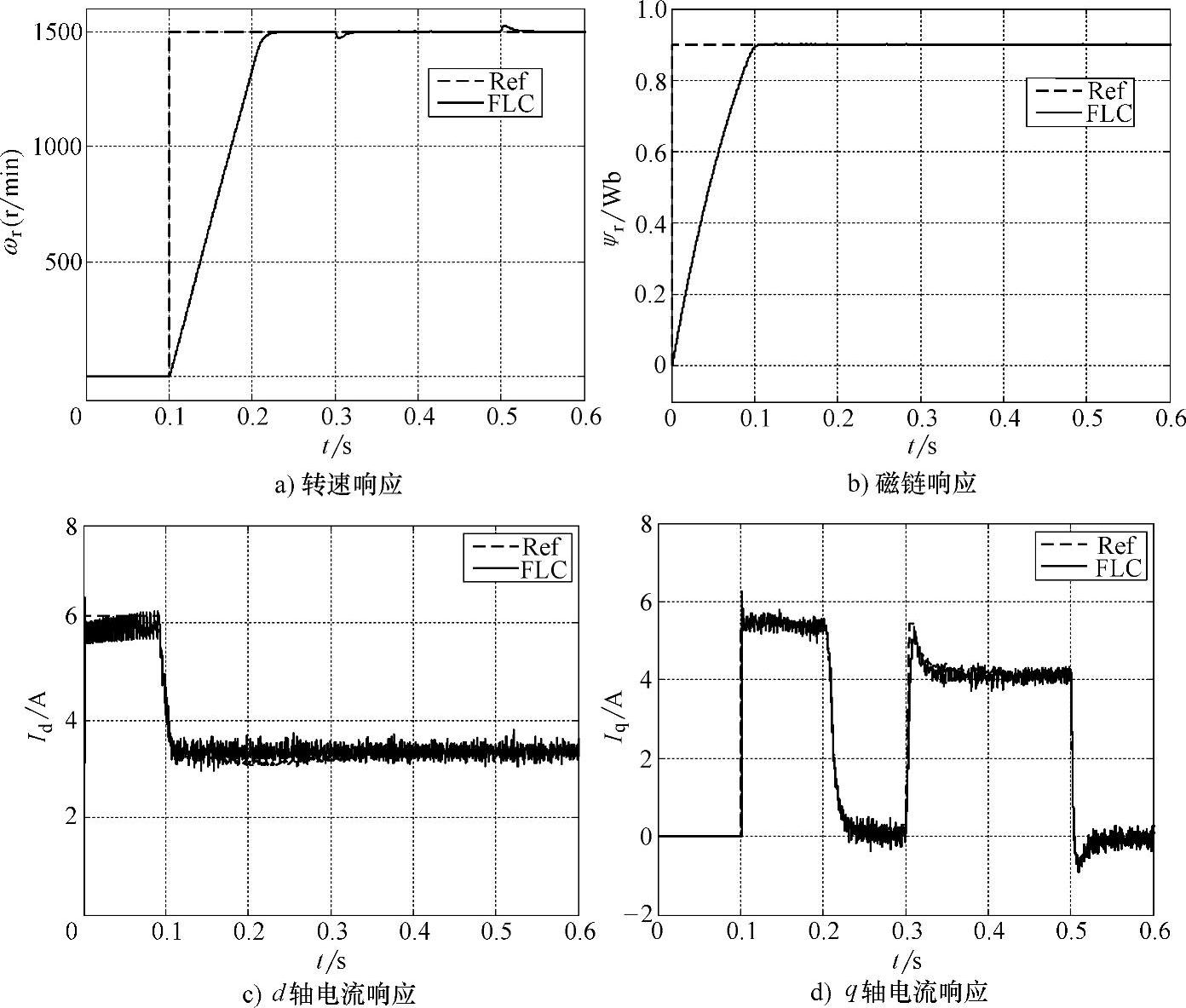
图5-23 采用FLC控制时的仿真波形