异步电机是一个非线性、多变量、强耦合的复杂系统，为了研究方便，通常做如下假设：

1）电机定、转子三相绕组完全对称。

2）电机定、转子表面光滑，无齿槽效应。

3）电机气隙磁动势在空间中按正弦分布。

4）忽略磁饱和、磁滞和涡流的影响，不考虑铁心和导线的趋肤效应。

三相异步电机的电、磁方面均为对称，采用空间矢量来描述电机模型，形式比较简单清楚，很多文献对此都有介绍，这里不再赘述。异步电机在以任意转速ω_k旋转的参考坐标系下的数学模型如式（5-1）～式（5-3）所示。采用任意参考坐标系的好处是很容易得到在静止坐标系、转子坐标系和同步旋转坐标系下的模型。

（1）电压方程

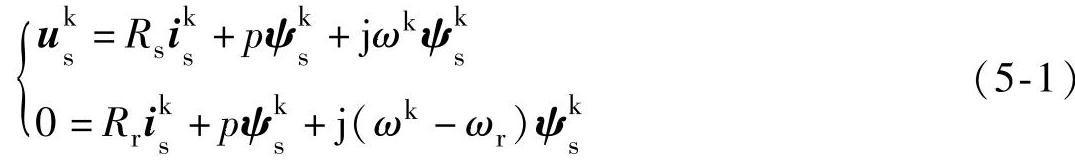
（2）磁链方程

（3）运动方程

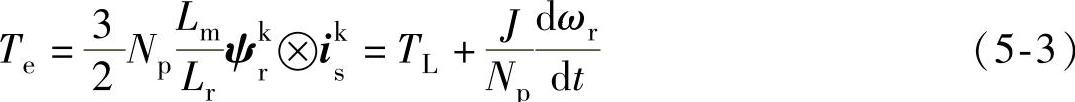
式中 R_s，R_r——定子和转子绕组电阻；

L_m，L_s，L_r——定子和转子绕组互感、定子自感和转子自感；

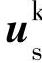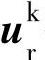，——任意转速坐标系下的定子和转子电压矢量；

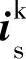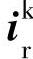，——任意转速坐标系下的定子和转子电流矢量；

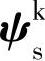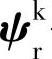，——任意转速坐标系下的定子和转子磁链矢量；

ω_r，ω^k——电机转子转速和任意转速参考坐标系的转速；

T_e，T_L——电磁转矩和负载转矩；

J——转动惯量；

N_p——极对数。

为了便于用现代控制理论分析电机，通常要把电机数学模型改用状态方程来表示。常见的组合是定子电流和转子磁链、定子电流和定子磁链，以及定子磁链和转子磁链。转子电流不可测量，很少被选择作为状态变量。这里总结推导了这三种组合形式状态变量在任意转速坐标系下的电机状态方程，描述如下：

（1）定子电流和转子磁链

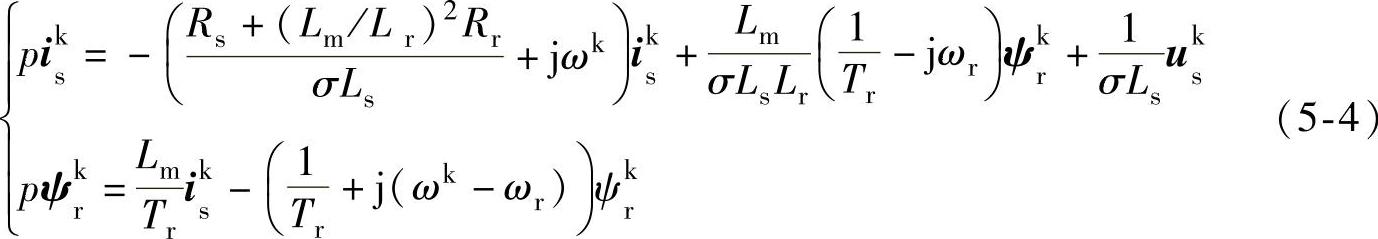(www.daowen.com)

（2）定子电流和定子磁链

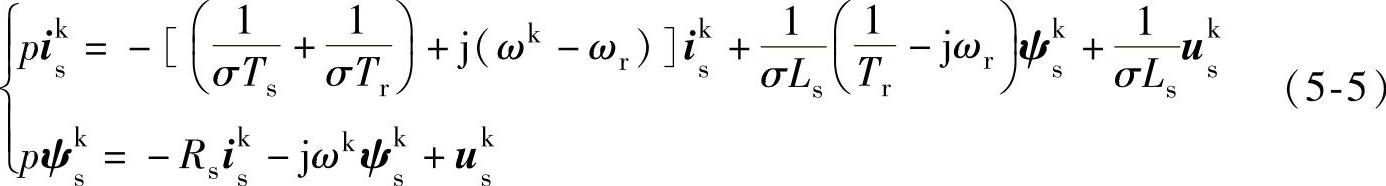
（3）定子磁链和转子磁链

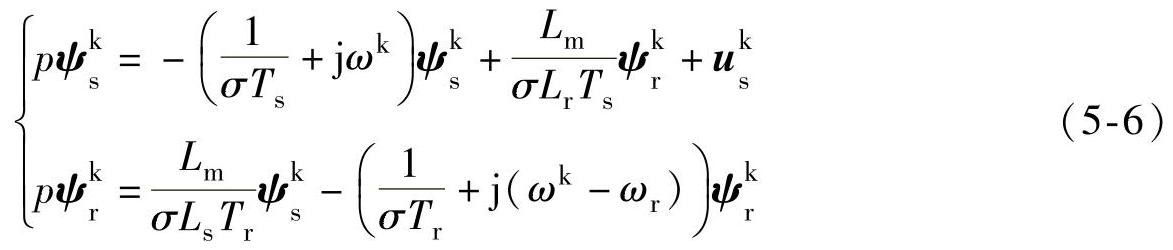
式中 σ=1-L²_m/（L_sL_r），T_s=L_s/R_s，T_r=L_r/R_r

由式（5-1）和式（5-2）消去定子磁链和转子电流，最终可得不含定子磁链和转子电流的任意旋转坐标系下的电机电压方程为

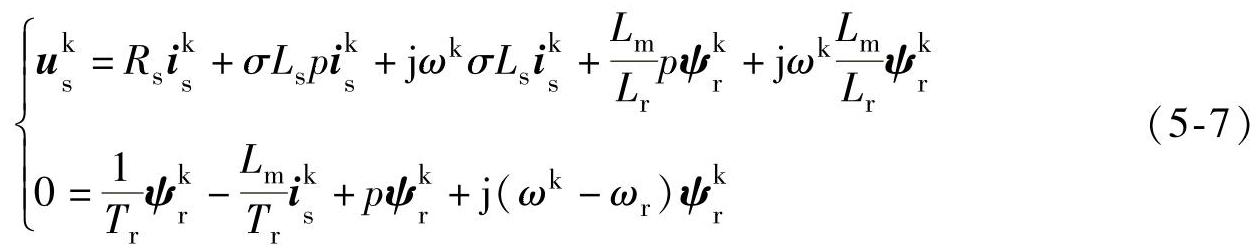
令ω^k为转子磁链的同步角速度ω_e，且令d轴与转子磁链的方向重合，即ψ_rd=ψ_r，ψ_rq=0，代入上式，展开成分量形式，最终可得电压方程为

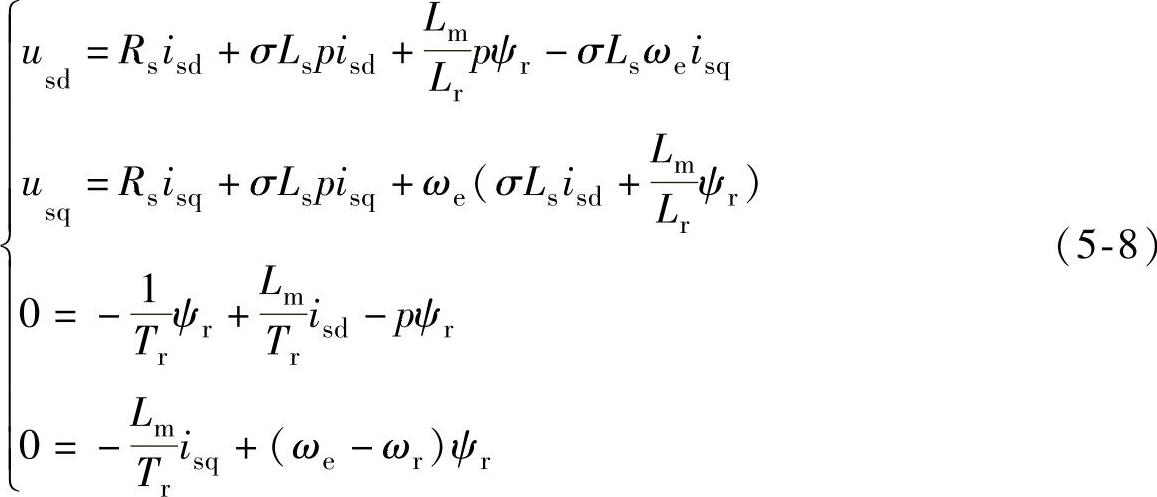
由式（5-8）中的d轴转子电压方程可得转子磁链和d轴电流的关系为

由式（5-8）中的q轴转子电压方程可得转差的表达式为

在转子磁场定向的条件下，电磁转矩也相应地简化为

式（5-9）表明转子磁通只与定子的d轴电流有关，式（5-11）表明在转子磁通恒定时转矩正比于定子q轴电流，相应的定子电流的d轴分量和q轴分量分别解耦为励磁电流和转矩电流。式（5-8）中的定子电压方程表明在略去反电动势引起的交叉耦合项后，可以由d轴电压来控制转子磁通，q轴电压来控制电磁转矩。

高性能无速度传感器异步电机转子磁场定向矢量控制系统中，包括四个闭环，即励磁电流内环、磁链外环、转矩电流内环和速度外环，共有四个调节器。调节器的整定设计是该系统的重要一环，调节器参数设计合适与否会直接影响整个系统的控制性能。

图5-1所示为两相同步旋转坐标系下基于转子磁场定向的异步电动机闭环系统框图。由图中虚线框电机模型可以看出，励磁电流环与转矩电流环之间是相互耦合的，不能通过两轴电压来单独控制励磁电流i_sd和转矩电流i_sq，即电流内环不是单变量线性系统，不能直接使用单变量线性系统工程设计方法整定调节器参数。因此，必须首先对电压进行解耦，把耦合闭环系统改造成单变量线性系统。

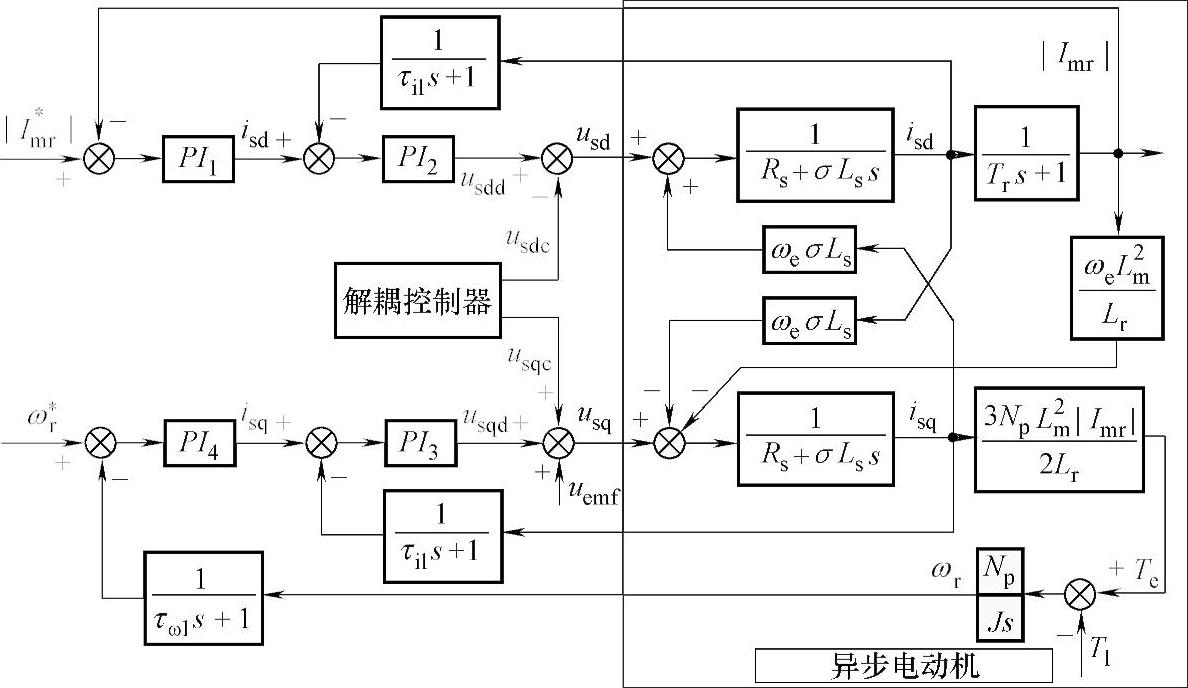
图5-1 异步电动机闭环系统框图

参考文献[1]引入了非线性补偿来设计解耦控制器，消除励磁电流环和转矩电流环之间的耦合。参考文献[2]指出了矢量控制系统中电流控制、转速控制和磁链控制中都存在耦合，并提出了相应的解耦方法。针对单输入单输出系统，参考文献[3]采用LQR方法分别对一阶系统、二阶系统和高阶系统进行了调节器最优设计。本章根据参考文献[4]的动态解耦方法提出了一种改进的动态电压解耦控制器对定子电压进行解耦，然后运用单变量线性系统工程设计方法对电流内环和速度、磁链外环各调节器参数进行了详细的分析和设计，总结了一套针对异步电动机无速度传感器矢量控制系统的PI调节器整定方法。实验结果验证了其良好的稳、动态性能和抗干扰性。

随着控制理论的发展，一些先进的控制理论如自适应控制或者智能控制已经渗透到电机控制中去。典型代表如滑模控制、模糊控制等，这类方法通常对电机参数变化和负载扰动具有一定鲁棒性，而且对数学模型依赖性小，是比较理想的方法^[5]。本章将滑模控制应用于矢量控制中的速度和磁链外环以及电流内环，提出并设计了一种全滑模无速度传感器矢量控制。另外，还将模糊控制应用到矢量控制中，提出了一种外环采用模糊控制内环采用PI加解耦的方法。将上述控制策略应用在无速度传感器直接矢量控制中，以期在改善系统动静态性能的同时，提高系统对参数变化和负载扰动的鲁棒性。