通过图4-19所示的异步电机无速度传感器矢量控制综合实验平台来验证辨识算法对电机参数的辨识效果。实验所用异步电动机额定参数为：额定功率P_n=4kW；额定电压U_n=380V；额定电流I_n=8.8A；额定转速ω_n=1440r/min；极对数P=2。DSP系统时钟设为150MHz，PWM调制频率为3kHz。功率模块采用三菱的PM50RSA120，电流信号检测采用LEM的霍尔传感器LA58-P，母线电压信号检测采用宇波的霍尔传感器CHV-25P。相电压信号通过PWM占空比和母线电压值来估算，转速通过算法估算。信号采样频率为3kHz，硬件模拟滤波为一阶RC低通滤波，滤波时间常数τ=0.001s，三阶巴特沃思数字滤波器截止频率为100Hz。电机运行频率为5Hz。

图4-32所示为电机5Hz运行时未进行电压补偿的估算相电压与采样电压波形比较，可以看出未补偿的相电压估计幅值偏大，相位滞后。图4-33所示为电机5Hz运行时进行电压补偿后的估算相电压与采样电压波形比较，可以看出补偿后的相电压估计结果与采样电压的幅值和相位都基本一致。

图4-32 5Hz运行时补偿前的相电压估算

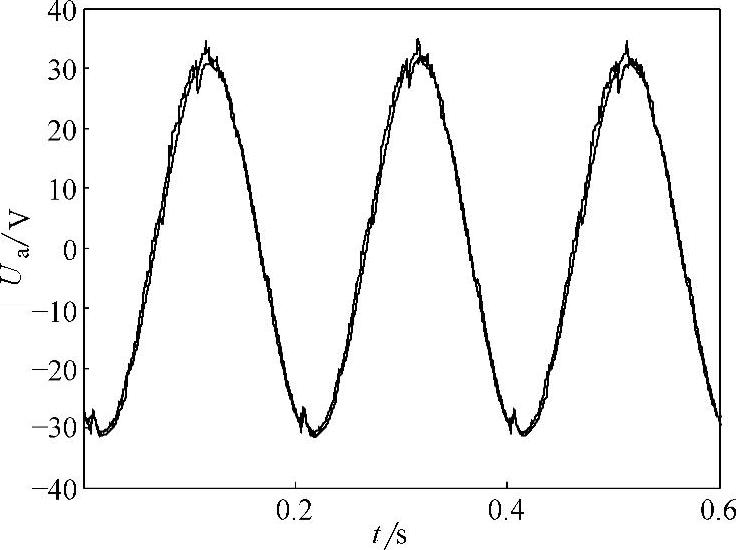
图4-33 5Hz补偿后的电压估算

辨识获得的电机参数如表4.7所示，表中参照值是通过高精度LCR表和国外高性能变频器辨识结果为依据获得的。参数辨识递推曲线如图4-34～图4-37所示，图中虚线为参照值。

表4-7 辨识实验结果比较

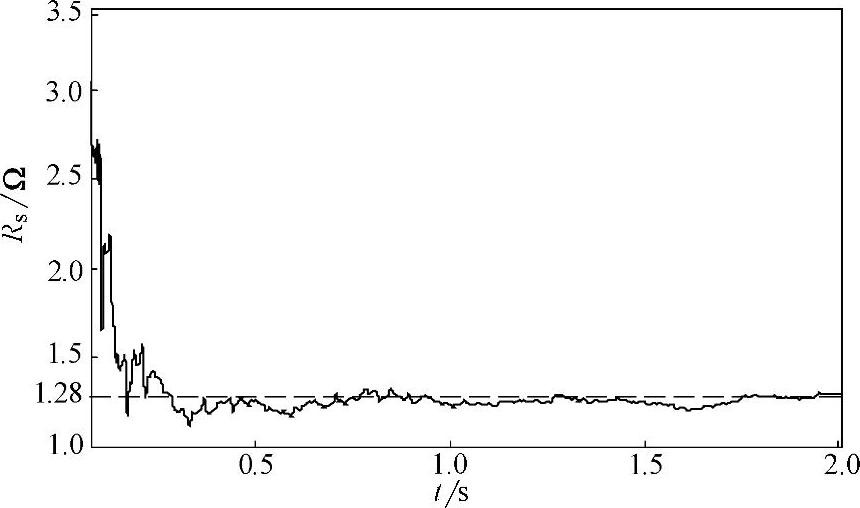
图4-34 定子电阻辨识过程曲线

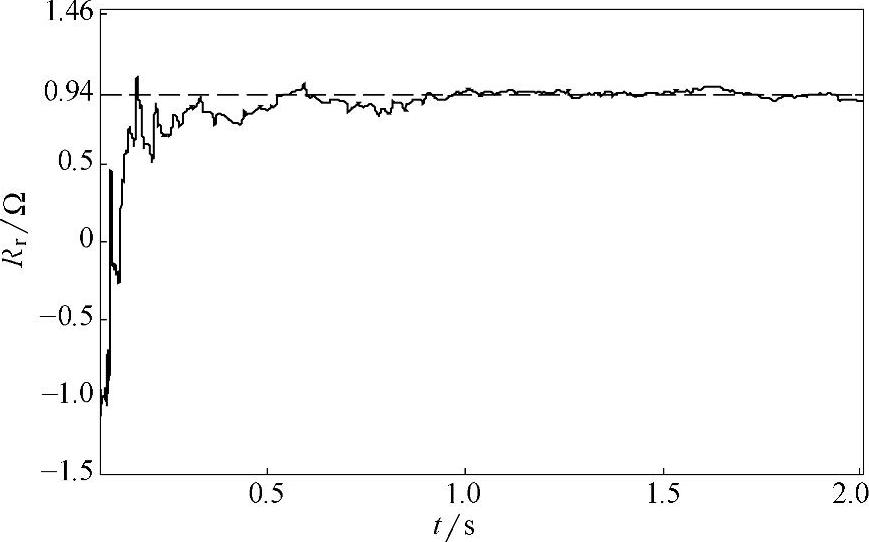
图4-35 转子电阻辨识过程曲线(www.daowen.com)

图4-36 定转子电感辨识过程曲线

图4-37 互感辨识过程曲线

从实验结果中可以看出，辨识值和参考值存在一定的误差，而仿真中的辨识结果与真实值基本无误差。误差原因分析如下：

1）电机模型误差。辨识用的电机数学模型与真实电机是存在一定误差的。另外，辨识用的电机数学模型做了近似处理，假定了转速稳定不变，忽略了转速的导数项。实际中转速是在设定值附近上下波动变化的。仿真中的电机是按照电机数学模型建立的，所以仿真中不存在电机模型误差。

2）采样误差。实验中由于噪声和电磁干扰，会造成电流采样不准确。同时由于硬件电路中元器件误差，使电流采样通道的滤波时间常数与理论计算值会有一定误差，造成电流相位变化。而仿真中采样是纯理想化的，不存在采样误差。

3）电压估算误差。电机相电压是通过PWM占空比和母线电压估算出来的，不是经由AD采样获取的，尽管进行了死区和管压降补偿，效果明显好于未补偿的电压估算，但并不能实现完全补偿，从而影响辨识精度。而仿真中未设定死区和管压降，电压估算很理想化。

4）转速估计误差。电机转速是通过一定的算法估算出来的，由于估算方法中需要这些电机初始参数和电压、电流信号，电机的初始参数是通过离线辨识获得的，存在辨识误差；电压信号存在估算误差，电流信号存在采样误差，这些误差会造成转速的估计误差。仿真中电机参数是已知的，不存在参数辨识误差，不存在电压估算误差，也不存在采样误差，所以转速估计误差很小。

5）参照值误差。实验中的参照值是通过高精度LCR表和国外高性能变频器辨识结果为依据获得的，不一定是真实值，会存在一定误差。而仿真中不存在这个问题。

6）巴特沃思数字滤波截止频率选择不合适。通过大量实验分析，我们发现该参数辨识方法对三阶巴特沃思数字滤波器的截止频率比较敏感。在一定的截止频率范围内，增大截止频率会使定子电阻的辨识值变大，转子电阻、电感和转子时间常数的辨识值变小；减少截止频率会使定子电阻的辨识值变小，转子电阻、电感和转子时间常数的辨识值变大。寻找巴特沃思数字滤波与辨识算法和电机参数的关系，从理论上能正确、合理地确定截止频率是下一步需要解决的问题。

通过实验发现，在巴特沃思数字滤波截止频率不变的情况下，在电机不同的运行频率下，辨识出的电机参数会有些变化，如果调整一下巴特沃思滤波器的截止频率，可以校正辨识出的电机参数。这对于实际应用增加了一定的困难，需要找出运行频率和巴特沃思滤波器截止频率之间的关系曲线，这对于实际应用增加了一定的困难，也是进一步需要研究的问题。