1.异步电机参数离线辨识数学模型

异步电动机在两相静止坐标系下的数学模型为^[23]

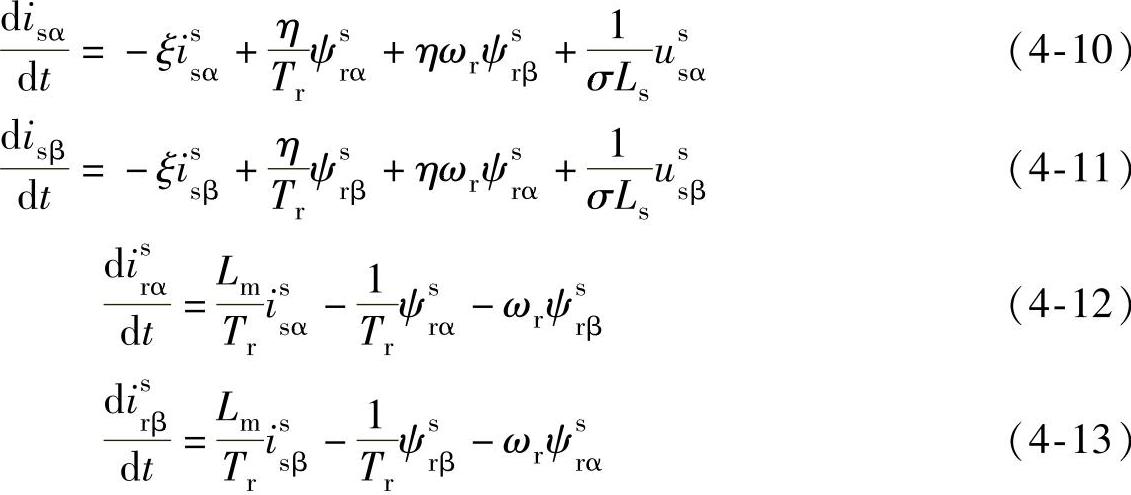
式中 ，，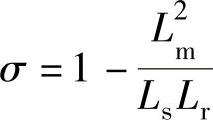

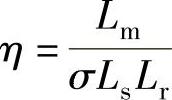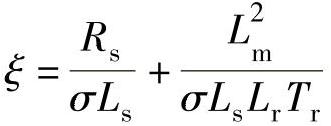
由于式（4-10）和式（4-11）中含有不可直接测量得到的转子磁链项ψ^s_rα和ψ^s_rβ，不能将其转换成最小二乘格式对电机参数进行辨识。通过代数运算和替代变换可将式（4-10）和式（4-11）中的不可测量转子磁链项消除^[19]，变为

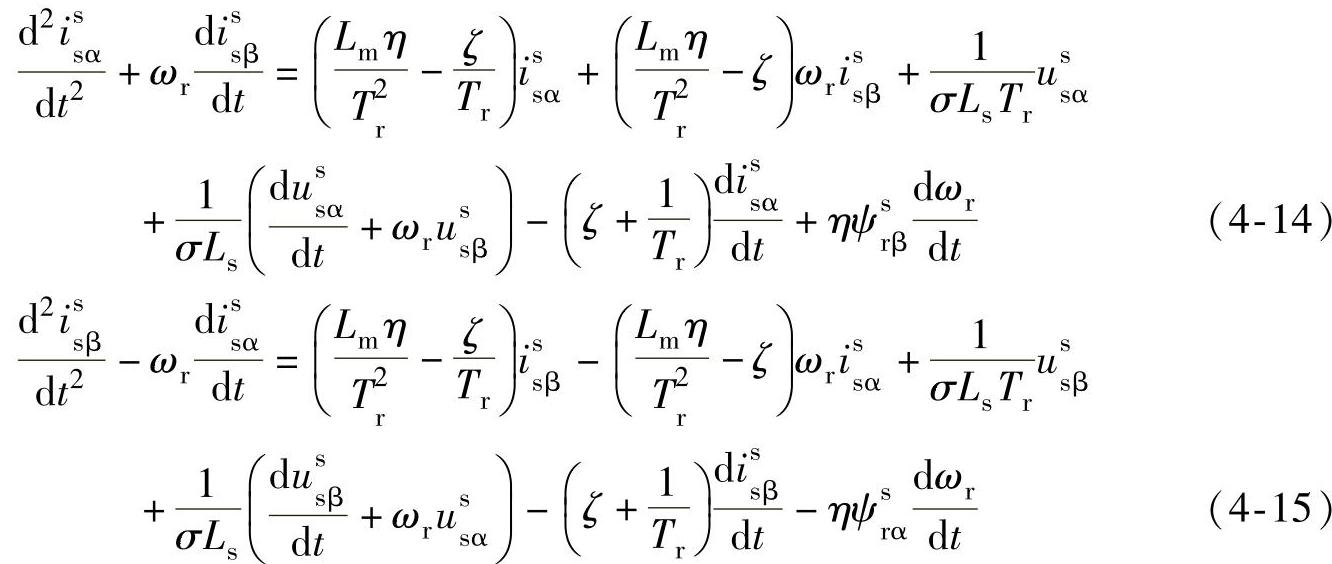
在对异步电机参数进行离线辨识时电机是静止不动的，即转速ω_r=0。因此式（4-14）和式（4-15）可以简化为

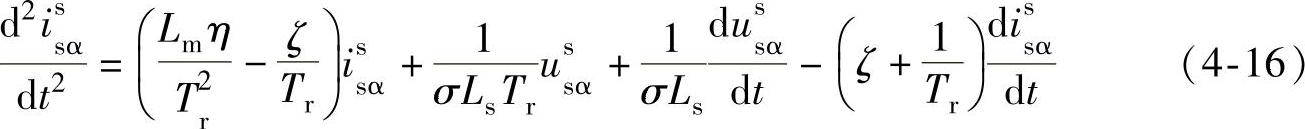
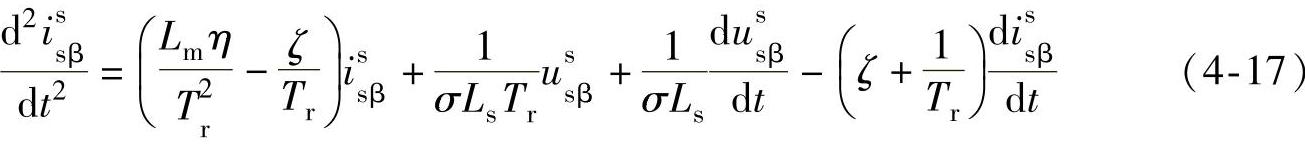
令

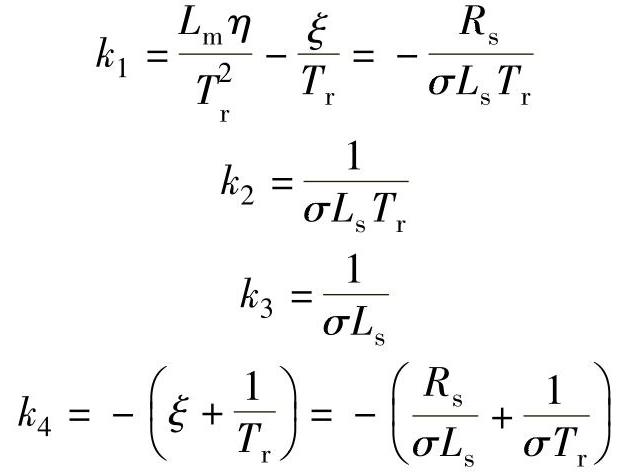
将式（4-16）和式（4-17）写成矩阵形式为

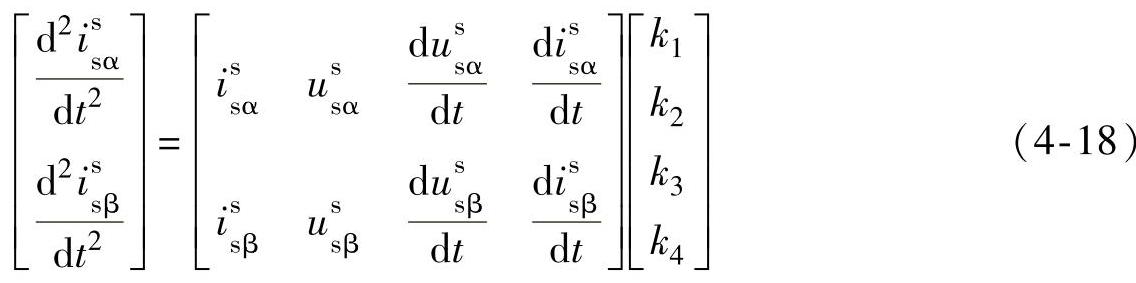
从上面4个k参数关系式中，能得到电机定子电阻R_s、定子电感L_s、转子时间常数T_r和漏磁系数σ的计算公式为

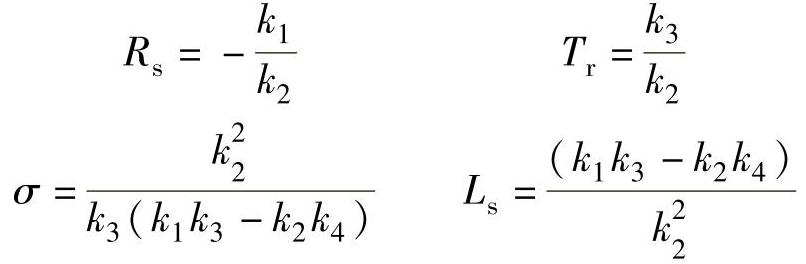
因为电机定子电感L_s和转子电感L_r相差很小，一般假定L_s=L_r，这样就能得到电机定转子互感L_m和转子电阻R_r的计算公式为

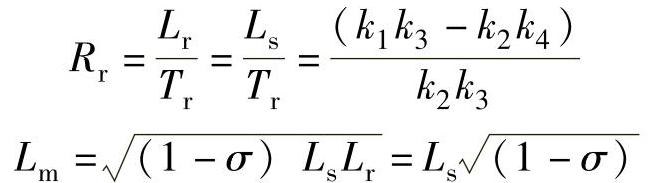
由于在进行电机参数离线辨识时，需要给电机注入激励信号，为了保持电机静止不动，在两相静止坐标系中只给α轴注入激励信号，β轴给零值。这样β轴的电压和电流值基本为零，式（4-18）可以简化为

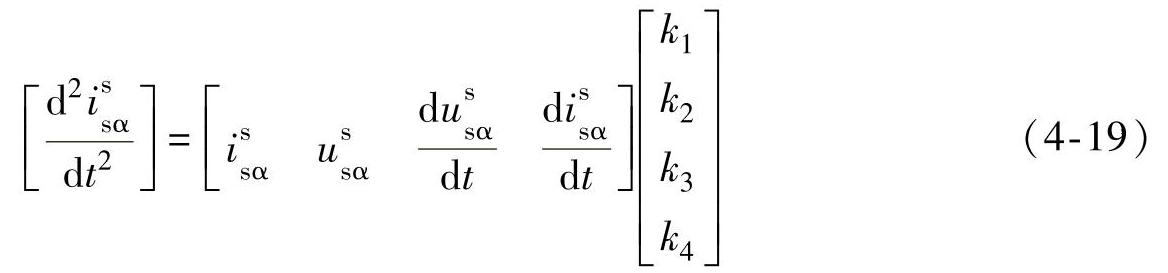
式（4-19）为连续时间模型，直接将其离散化，得离散化模型为式（4-20）。这里不用将电压和电流信号各阶导数离散化，而是直接获取其各阶导数值，具体参见下面第3部分“状态变量滤波器”。

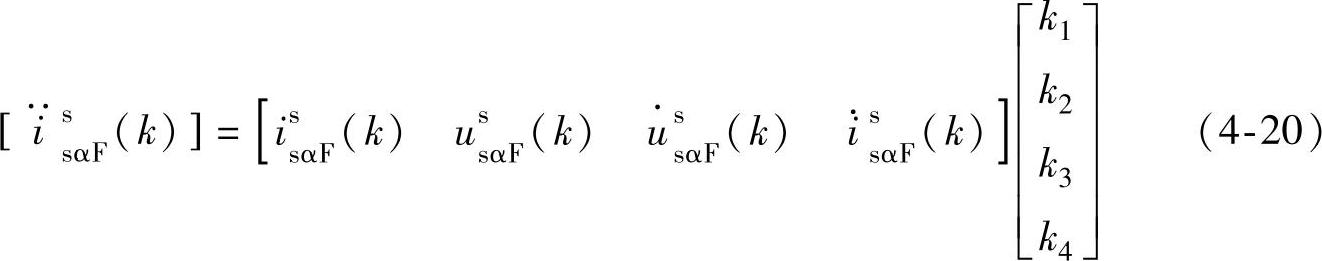
式中 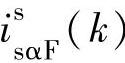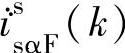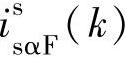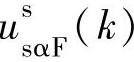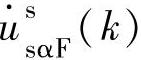，，，，——数字滤波后的值。

式（4-20）为一维模型，这样在采用递推最小二乘算法进行参数辨识时，避免了求K_N+1时出现的二维矩阵求逆运算问题，减少了计算量。

2.递推最小二乘（RLS）算法

最小二乘算法^[24]是系统辨识中参数估计的最基本方法。递推最小二乘算法应用最广，相比于一般最小二乘方法，它不需要大矩阵求逆运算，计算量小，计算速度快且收敛速度快，可实时在线应用。

为了应用最小二乘算法解决参数的最优估计问题，将式（4-20）改写为最小二乘格式为

式中 ；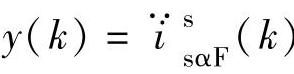

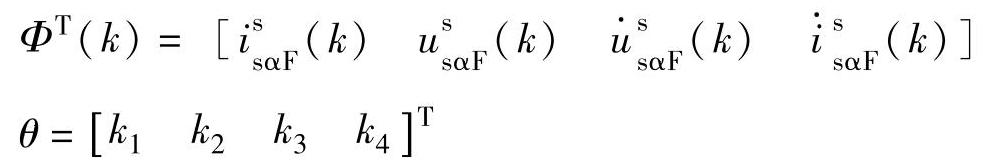
ξ（k）——模型残差。

其递推最小二乘算法为

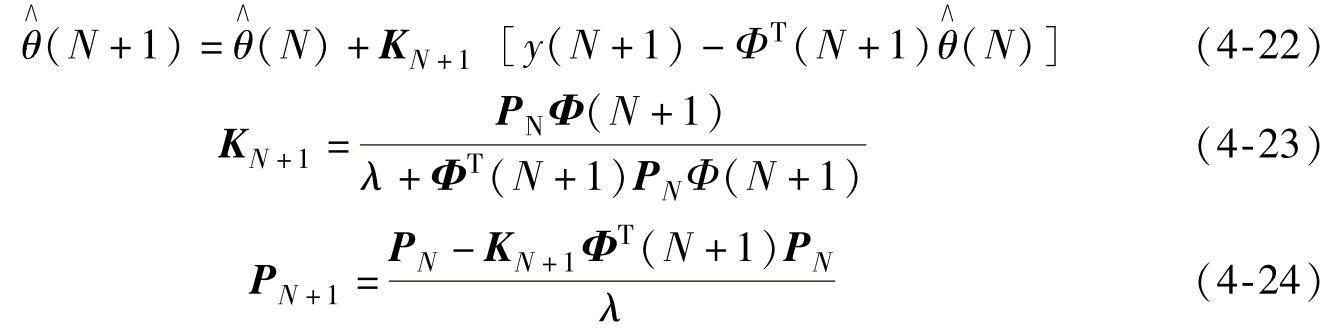
式中 K_N+1——增益矩阵；

P_N——协方差阵，其初始值为P₀=10^βI，I为单位矩阵，β一般取较大的正整数；

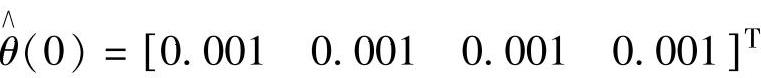，给定估计参数初值，取很小的值。

λ——遗忘因子（0＜λ≤1），使旧数据按指数衰减规律逐渐被“遗忘”掉，从而突出新数据的作用，有效地克服递推最小二乘法的“数据饱和”现象。λ的取值越小，“遗忘”的速度越快，但取值太小会使辨识的精度降低，波动变大。一般取λ∈[0.8，1]，离线辨识取λ=1。

3.状态变量滤波器

由于采集的电压和电流信号含有高次谐波和噪声，因此除了硬件上的模拟滤波外，还必须对信号进行数字滤波。加入滤波必然造成信号的衰减和时延，为了能够实现对参数的精确辨识，电压和电流信号必须同步和同比例。这就要求对电压和电流信号要进行相同的滤波。此外，从式（4-22）～式（4-24）中我们知道在采用递推最小二乘算法辨识参数时，除了需要采集的电压和电流信号外，还需要得到电流信号的一阶导数、二阶导数以及电压信号的一阶导数。参考文献[19]采用欧拉方法对信号的一阶导数和二阶导数离散化，将式（4-18）改写成差分方程的形式，然后运用递推最小二乘算法进行参数的辨识。我们知道，一个数值方法的局部截断误差越小，其计算结果的精确程度也越好。由于欧拉方法的局部截断误差为o（h²）^[25]，它是一个一阶方法，其计算结果精度较差。这里采用三阶巴特沃思数字滤波器对电压和电流信号进行滤波，三阶巴特沃思数字滤波器的传递函数系数可查表获得。将其传递函数转换成状态方程形式^[26]，写成能控规范型，便于后面求解运算。以滤波后的信号变量及其一阶导数和二阶导数作为其三个状态变量，采用改进的欧拉方法，以采样周期为步长，解微分方程，求解出状态变量的数值解。改进的欧拉方法的局部截断误差为o（h³），它是一个二阶方法，其计算结果精度比欧拉方法要高。这样通过上述方法既对信号进行了数字滤波，又直接得到了滤波后各个时刻信号的一阶导数和二阶导数，可直接得到离散化模型式（4-20），不用对其各阶导数进行离散化，简化了运算，提高了计算精度。

（1）巴特沃思滤波器

为了采用上述方法得到电压和电流信号的二阶导数，巴特沃思滤波器阶数必须为三阶或三阶以上。巴特沃思滤波器的阶数越高，其截止特性越好。为了减少运算量，能够实际应用实现，这里采用三阶巴特沃思滤波器。其传递函数为

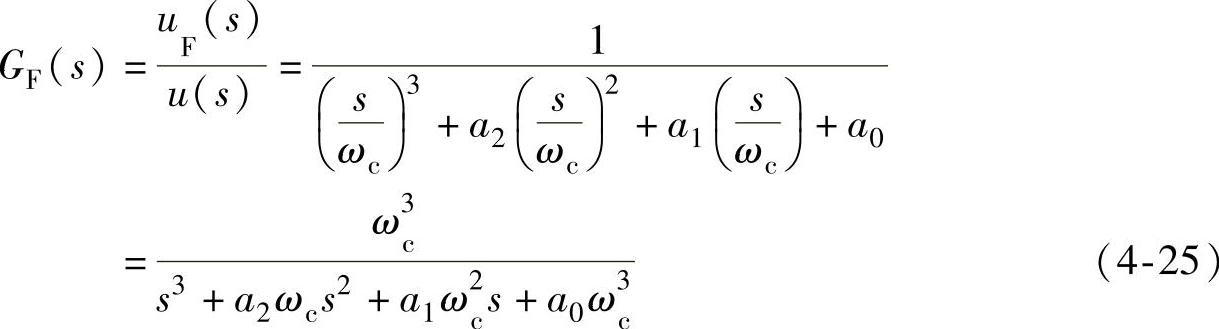
式中 ω_c——低通滤波器截止频率；

a₀，a₁，a₂——滤波器系数，可查表^[27]获得。

将式（4-25）转换成状态方程形式，写成能控规范型如下：

式中

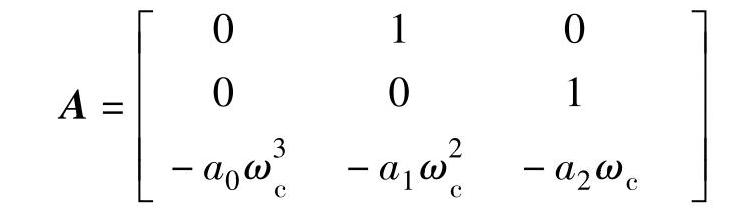
由式（4-26）可以看出，状态变量为滤波后的电压或电流信号及其一阶和二阶导数，下面的问题就是如何求解出这些状态变量。

（2）改进的欧拉方法

改进的欧拉方法是先利用欧拉公式对X（k）的值进行预估，然后利用梯度公式对预估值进行一次校正，故改进的欧拉方法又称预估校正方法。

预估值：

X_P（k）=X（k-1）+T[AX（k-1）+Bu（k）] （4-27）

式中 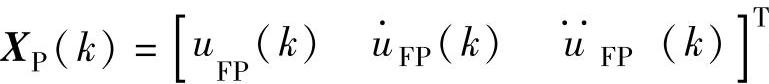——状态变量的预估数值解；

T——采样周期。由式（4-26）和式（4-27），能得到状态变量预估值为

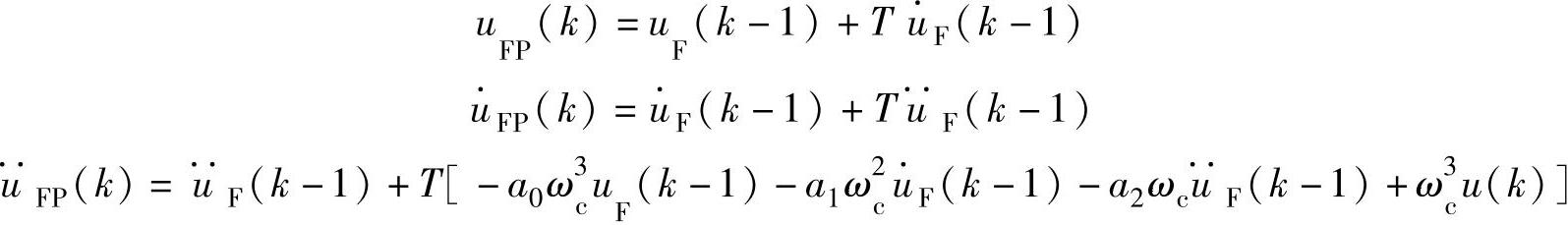
校正值为

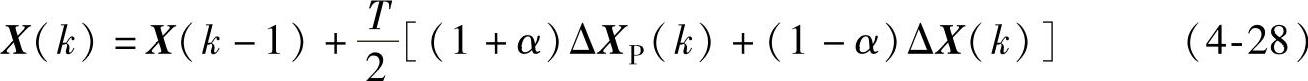
式中

ΔX_P（k）=AX_P（k）+Bu（k） （4-29）

ΔX（k）=AX（k-1）+Bu（k） （4-30）(www.daowen.com)

α——预估权重，α∈[0，1]；

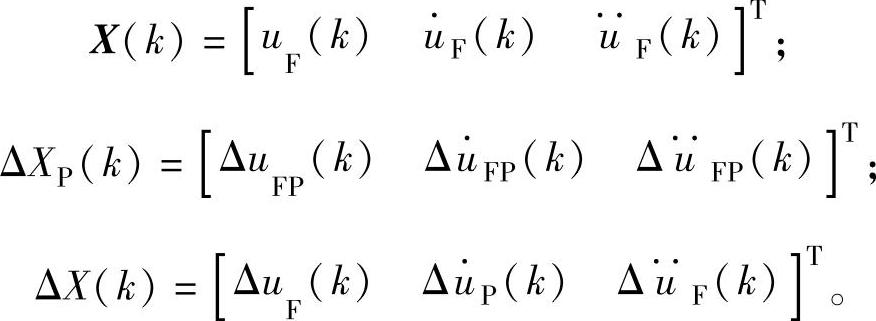
由式（4-28）～式（4-30），解得状态变量校正值为

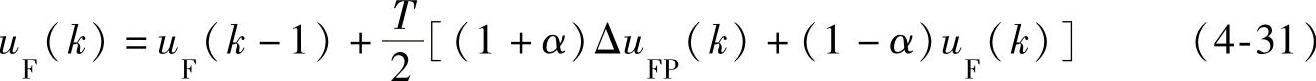
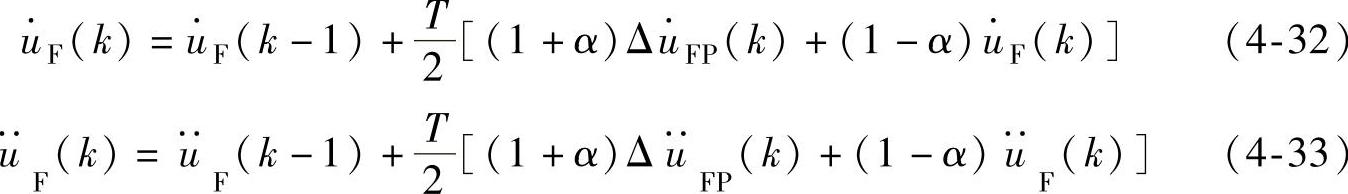
式中

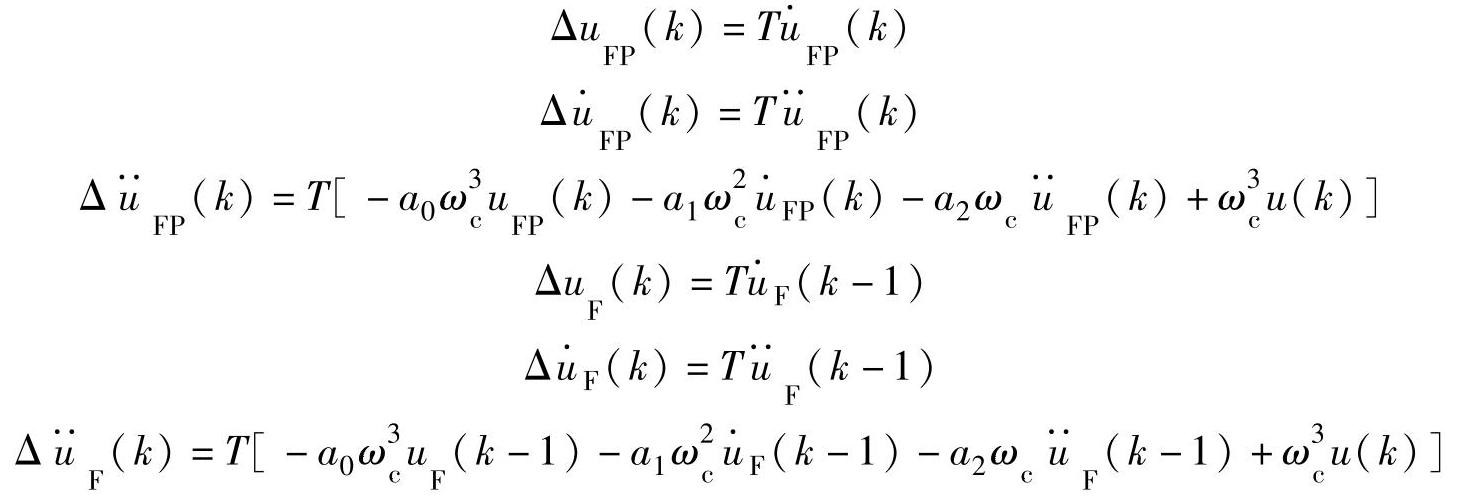
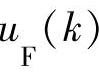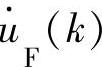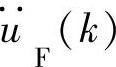，，即为最终状态变量数值解，其算法流程如图4-12所示。这样通过改进的欧拉方法获得了滤波后的电压或电流信号及其一阶和二阶导数的数值解，下面就可以运行辨识算法进行参数辨识了。

（3）伪随机激励信号

白噪声序列是一种具有各态历经性的随机信号，它在任意两个不同的时刻是不相关的，白噪声的谱密度在所有频率上相同。由于实际中纯粹的白噪声并不存在，采用最小二乘算法进行参数辨识时，为了充分能激励系统，得到参数的无偏性估计，这里采用伪随机信号作为系统的输入信号。伪随机信号^[28]是一种近似白噪声序列，接近白噪声的统计特性，可满足系统辨识对信号激励特性的要求。

伪随机信号可以通过线性反馈移位寄存器产生，伪随机信号的周期长度随着移位寄存器个数的增多而增大。移位寄存器个数相同的情况下，反馈连接方式的不同也会影响伪随机信号的周期长度。信号最大周期T=NΔt，Δt表示输入给移位寄存器的脉冲周期，N=2ⁿ-1表示移位寄存器个数为n时的最大长度伪随机信号序列，称为M序列。当t＞T时，又进入一个信号周期，后一个周期会复现前一个周期的信号。因此，M序列是一种长周期的信号，在一个周期内是随机性信号，当观测时间大于一个周期时便是确定性信号。在系统辨识中，利用的是它的随机性，因此信号的使用长度要小于一个周期。

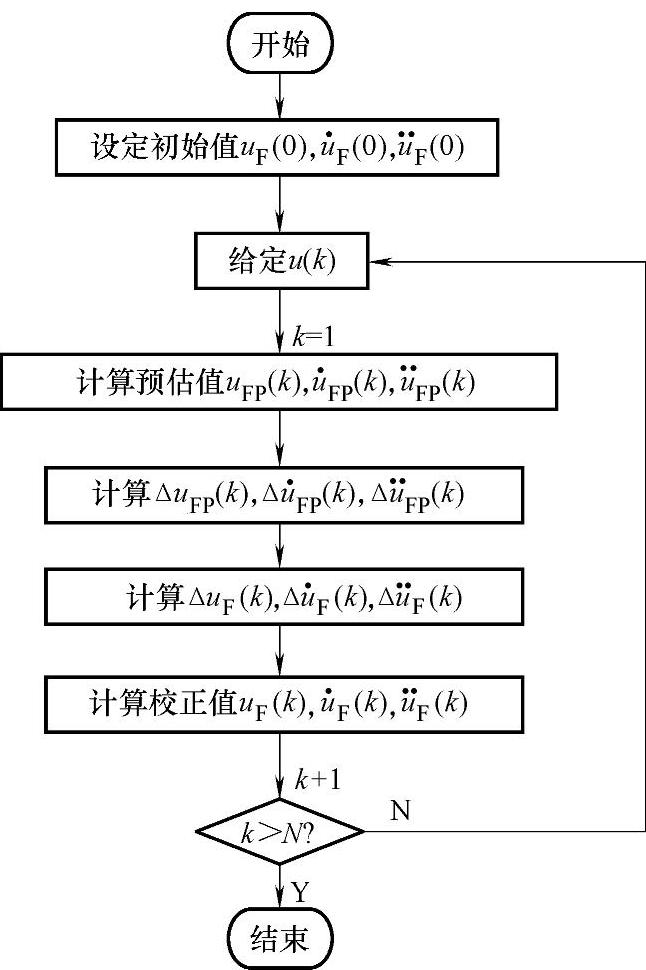
图4-12 预估校正方法流程图

在一个周期内，N越大，M序列的性质就越接近白噪声。因此，为了充分激励系统，提高辨识精度和稳定性，采用13级M序列触发器，其产生的M序列长度N=8191，如图4-13所示。每个寄存器的状态为1或-1，表示异或，相同输出-1，不同输出1。每一个移位脉冲作用后，各寄存器状态依次后移，C13C4C3C1依次异或后，结果输入给C1，C13状态为输出，即为产生的M序列。

图4-13 13级M序列触发器

4.仿真结果

利用MATLAB工具进行了仿真验证，仿真结构框图如图4-14所示。仿真选用的异步电机额定参数为：额定功率P_n=4kW；额定电压U_n=400V；额定频率f_n=50Hz；额定转速ω_n=1430r/min；极对数P=2。采样周期为0.00025s，采样数据长度为8000组。给定的电机参数和辨识获得的电机参数如表4-2所示。参数辨识递推曲线如图4-15～图4-18所示。

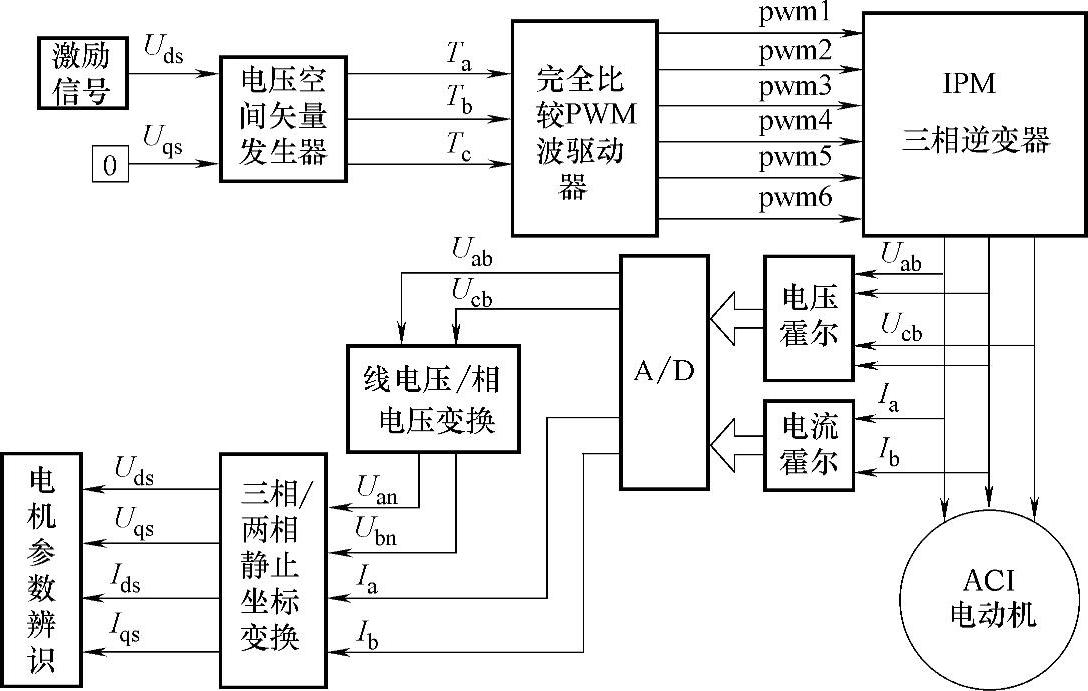
图4-14 参数辨识结构框图

表4-2 辨识仿真结果比较

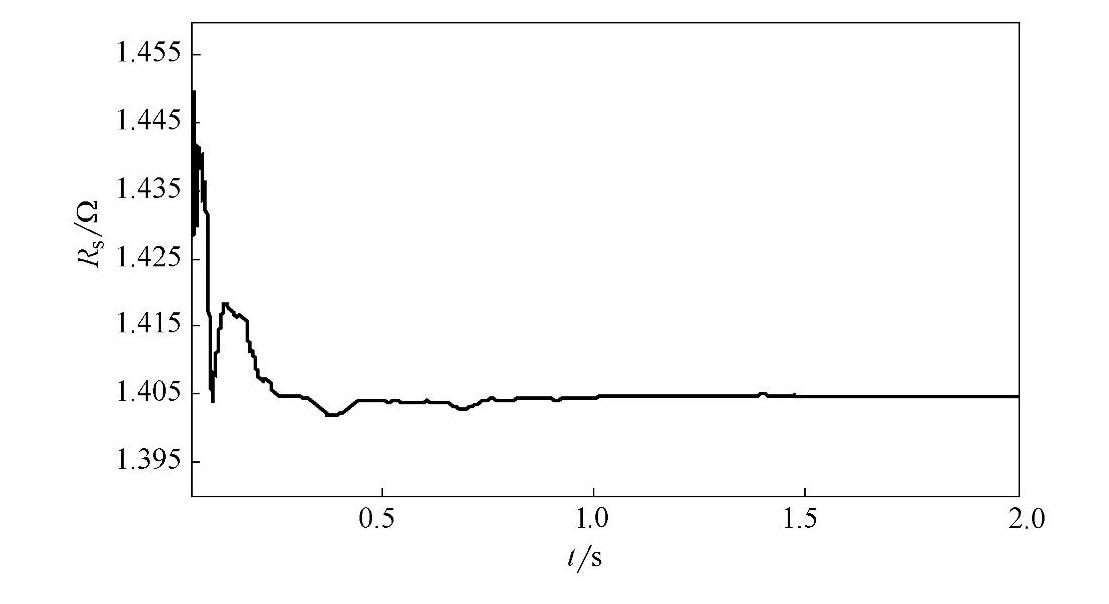
图4-15 定子电阻辨识过程曲线

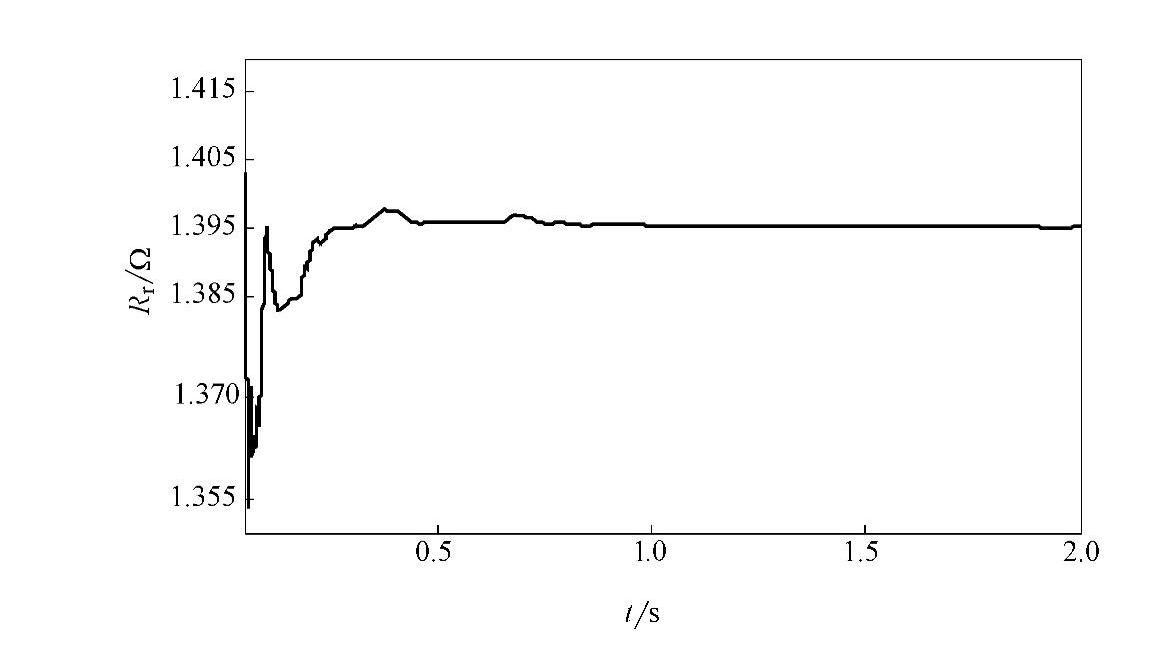
图4-16 转子电阻辨识过程曲线

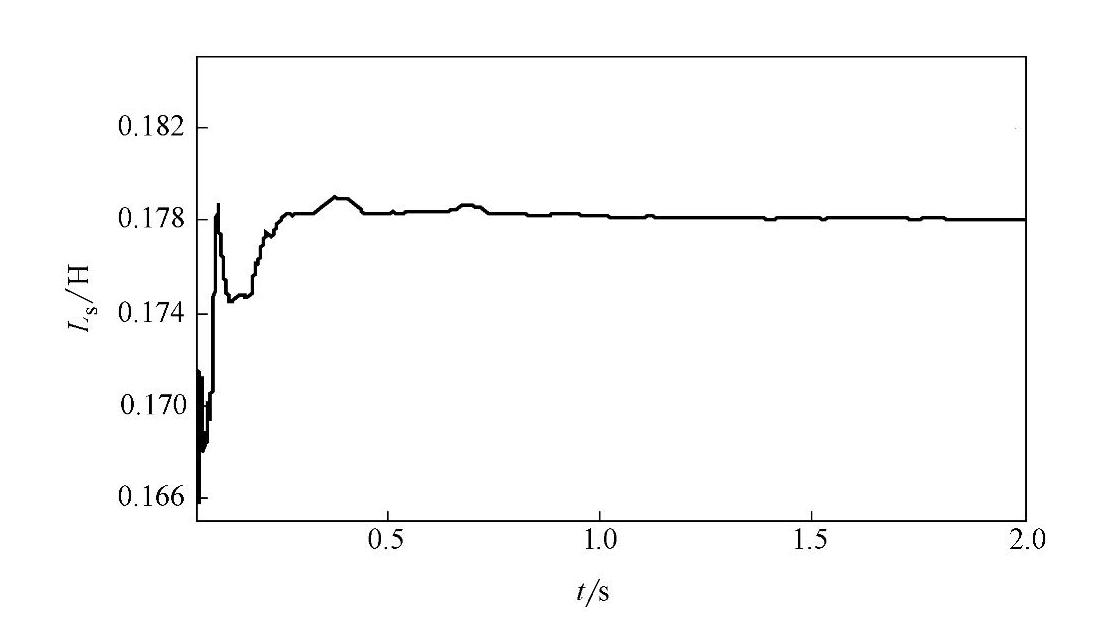
图4-17 定转子电感辨识过程曲线

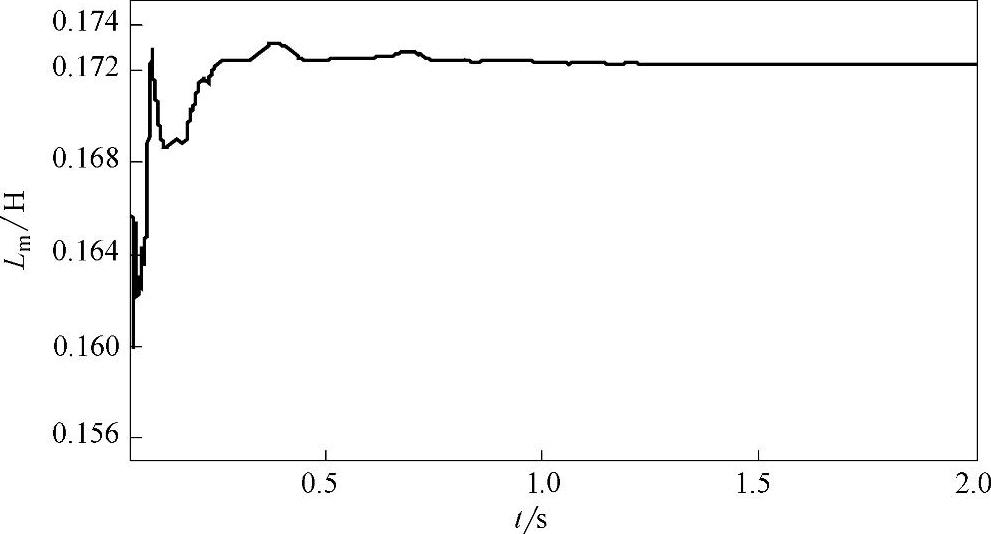
图4-18 互感辨识过程曲线

5.实验结果分析

图4-19所示为异步电机无速度传感器矢量控制综合实验平台，可以通过该实验平台来验证辨识算法对电机参数的辨识效果。整个控制系统采用TI公司的TMS320F2812 DSP芯片来实现辨识算法，实验所用异步电动机额定参数为：额定功率P_n=4kW；额定电压U_n=380V；额定电流I_n=8.8A；额定转速ω_n=1440 r/min；极对数P=2。DSP系统时钟设为150MHz，PWM调制频率为3kHz。功率模块采用三菱的PM50RSA120，电流信号检测采用LEM的霍尔传感器LA58-P，母线电压信号检测采用宇波的霍尔传感器CHV-25P。相电压信号通过PWM占空比和母线电压值来估算。信号采样频率为3kHz，硬件模拟滤波为一阶RC低通滤波，滤波时间常数τ=0.001s，三阶巴特沃思数字滤波器截止频率为100Hz。

图4-19 异步电机无速度矢量控制系统综合实验平台

图4-20所示为参数辨识实时监控界面。辨识获得的电机参数见表4-3所示，表中参照值是通过高精度LCR表和国外高性能变频器辨识结果为依据获得的。参数辨识递推曲线如图4-21～图4-24所示，图中虚线为参照值。

表4-3 辨识实验结果比较

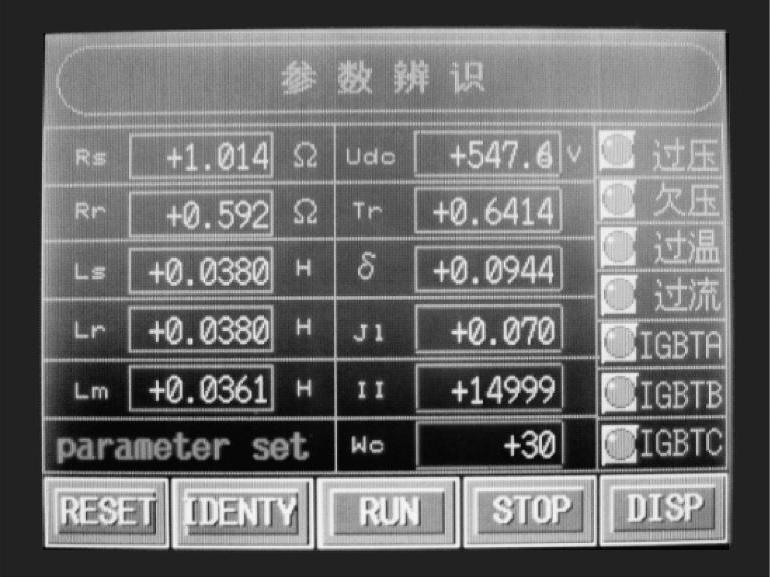
图4-20 参数辨识实时监控界面

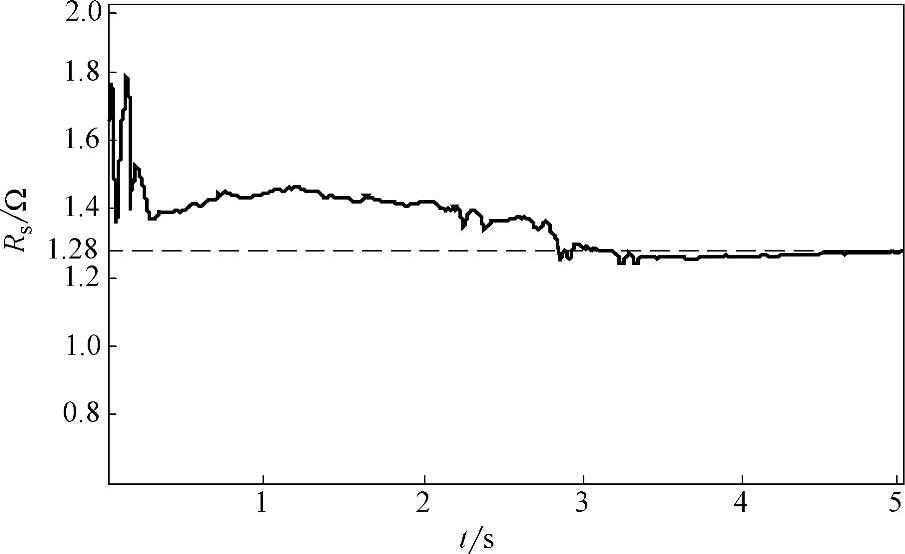
图4-21 定子电阻辨识过程曲线

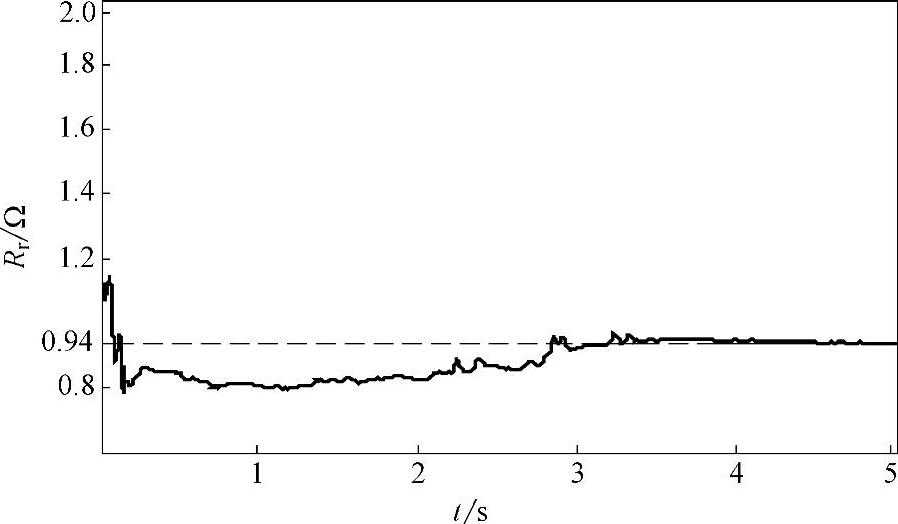
图4-22 转子电阻辨识过程曲线

另外，对不同功率的异步电动机也进行了参数辨识实验。表4-4所示为同一电机4次辨识结果比较，表4-5所示为不同电机辨识结果比较。从表中能看到该辨识方法具有很好的稳定性和通用性。

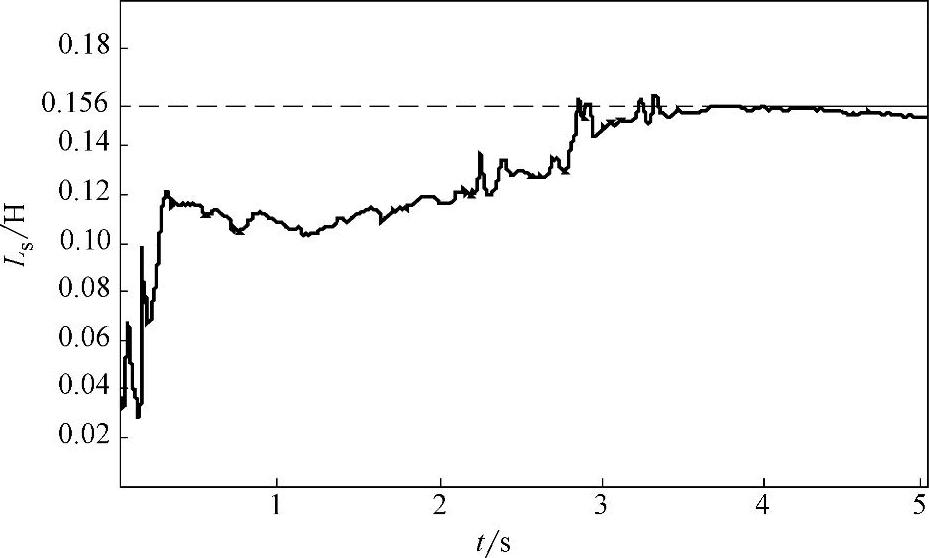
图4-23 定转子电感辨识过程曲线

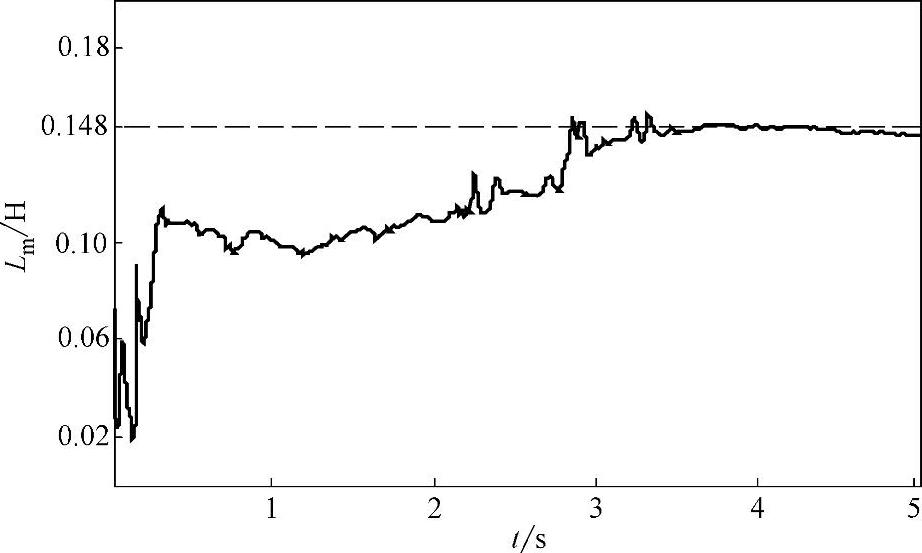
图4-24 互感辨识过程曲线

表4-4 同一电机4次辨识结果比较

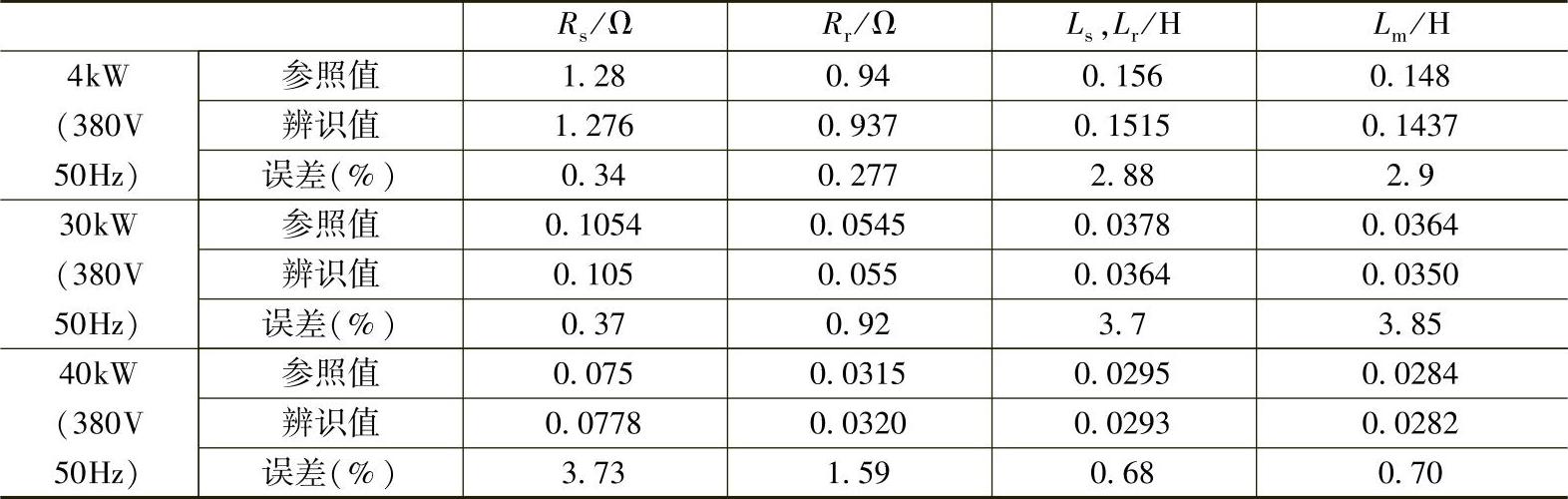
表4-5 不同电机辨识结果比较

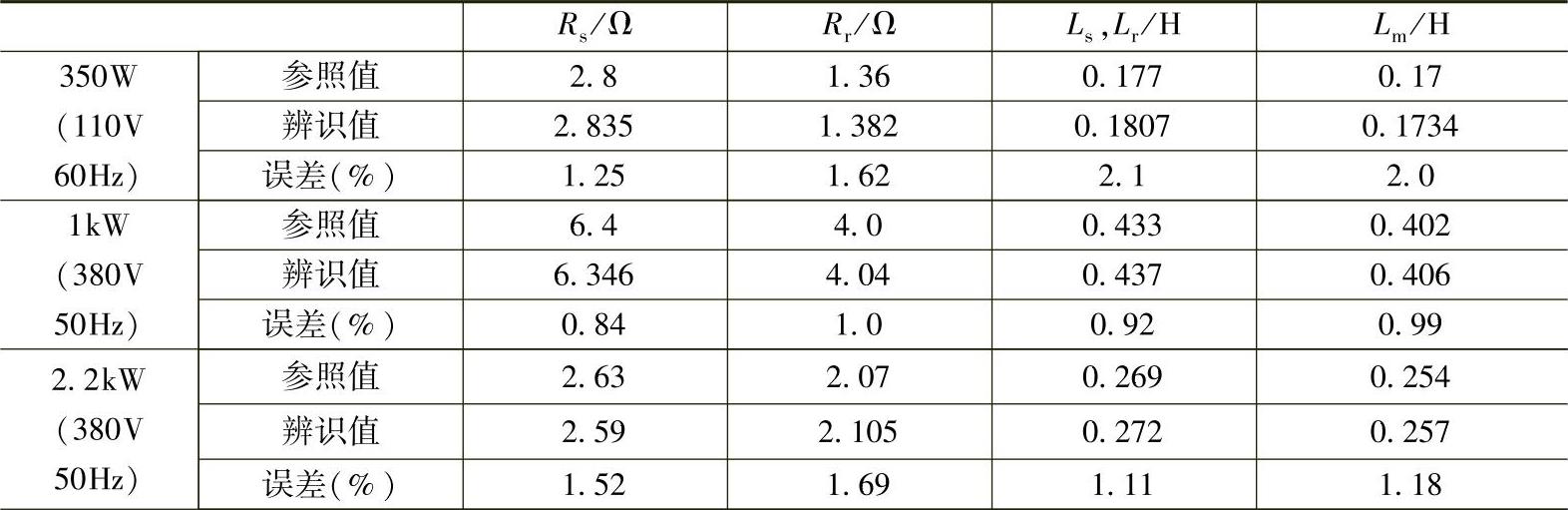
（续）

从实验结果中，辨识值和参考值存在最大4%的相对误差，而仿真中的辨识结果与真实值基本无误差。误差原因分析如下：

1）电机模型误差。辨识用的电机数学模型与真实电机是存在一定误差的。仿真中的电机是按照电机数学模型建立的，所以仿真中不存在电机模型误差。

2）采样误差。实验中由于噪声和电磁干扰，会造成电压、电流采样不准确。同时由于硬件电路中元器件误差，使电压和电流采样通道的滤波时间常数不一致，造成电压和电流相位差变化，不是实际的电机相位差。而仿真中采样是纯理想化的，不存在采样误差。

3）参照值误差。实验中的参照值是通过高精度LCR表和国外高性能变频器辨识结果为依据获得的，不一定是真实值，会存在一定误差。而仿真中不存在这个问题。

4）巴特沃思数字滤波截止频率选择不合适。通过大量实验分析，我们发现该参数辨识方法对三阶巴特沃思数字滤波器的截止频率比较敏感。在一定的截止频率范围内，增大截止频率会使定子电阻的辨识值变大，转子电阻、电感和转子时间常数的辨识值变小；减少截止频率会使定子电阻的辨识值变小，转子电阻、电感和转子时间常数的辨识值变大。寻找巴特沃思数字滤波与辨识算法和电机参数的关系，从理论上能正确、合理地确定截止频率是下一步需要解决的问题。