在某些情况下由于电机和负载难以分离，空载实验无法进行，所以需要开发电机在静止条件下的参数辨识算法。异步电机在正弦稳态下的等效电路如图4-8所示，更一般的等效电路可以表示为图4-9，其中a可以是任意实常数^[22]。

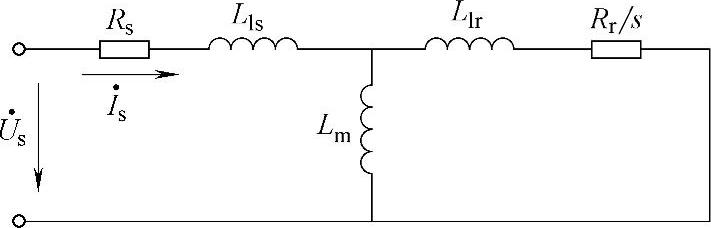
图4-8 正弦稳态等效电路

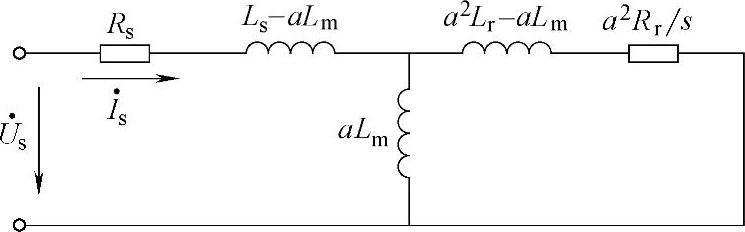
图4-9 一般形式等效电路

令图4-9中a=L_m/L_r，可得适用于说明RFOC稳态的T-Ⅰ型等效电路。另外，由于是静止条件下，所以s=1，如图4-10a所示，为便于说明，重新标示其中的电阻电感，如图4-10b所示。如果令a=L_s/L_m，可得适用于说明DTC稳态的T-Ⅱ型等效电路，它用导纳描述比较方便，而T-Ⅰ型电路用阻抗描述比较方便。

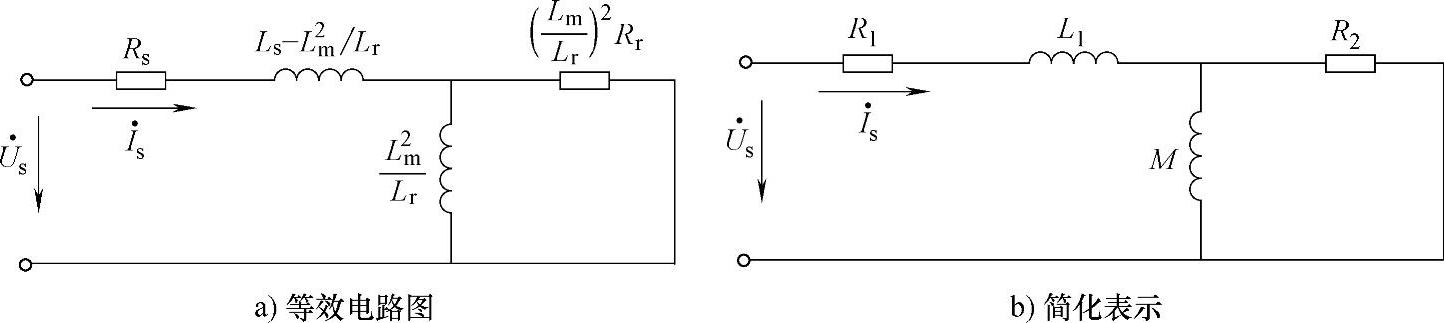
图4-10 T-I型异步电机稳态等效电路

在静止条件下测试电机参数是通过给电机施加两次不同定子频率的交流激励，然后由两次的阻抗得到电机参数，依然使B相和C相短接，基波电压和电流利用FFT得到。由图4-10b可以得到电机的等效阻抗Z_k如式（4-7）所示，并记R_2k=R_k-R₁。

Z_k=R₁+jX₁+R₂‖jX_m=R_k+jX_k （4-7）(www.daowen.com)

假设已经求出两个角频率分别为ω₁和ω₂的单相交流激励下的等效阻抗Z_k（ω₁）和Z_k（ω₂），则通过求解非线性方程组，可以推导出图4-10b所示电路中的几个参数，表示为式（4-8），然后根据上述几个参数可以得到真正的电机参数如式（4-9）所示。

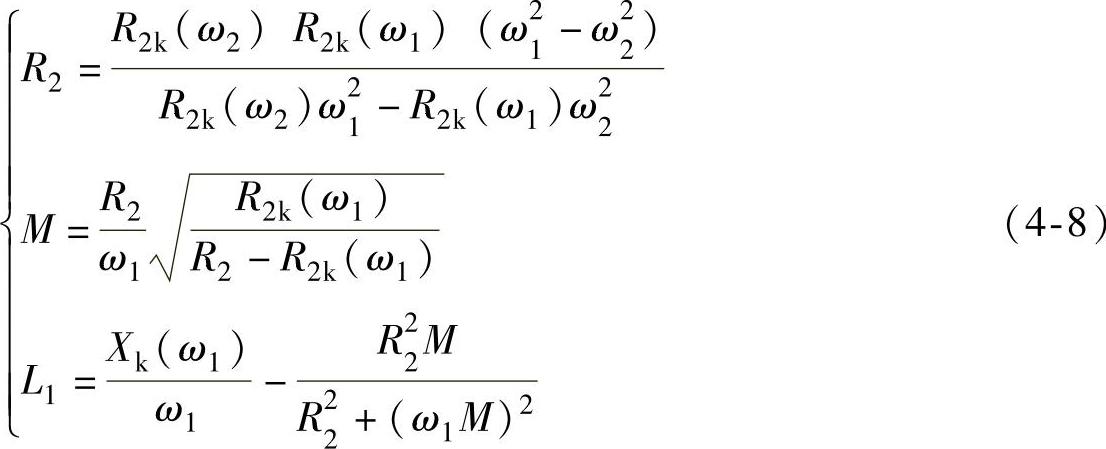
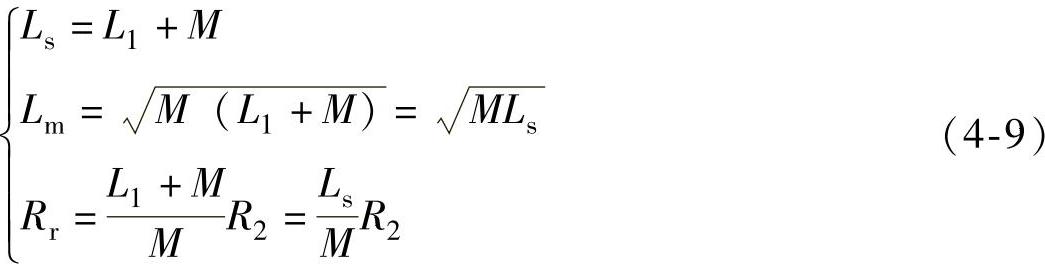
需要指出的是，式（4-8）和式（4-9）只是理想推导得到的结果，在实际应用中，由于非线性方程组的复杂性，采用直接解析求解的方法很难得到准确结果，通常是采用迭代的方法进行求解，由式（4-8）得到的解析解可以作为迭代的初值。注意到Z_k（ω₁）和Z_k（ω₂）展开成实部和虚部共有四个方程，而要求解的变量为三个，所以这里存在一个冗余方程。实际计算表明R₂和L₁的求解结果比较稳定，关键是确定M的值，使得X_k（ω₁）和X_k（ω₂）的测量值与计算值相符即可。具体的迭代过程流程图如图4-11所示。

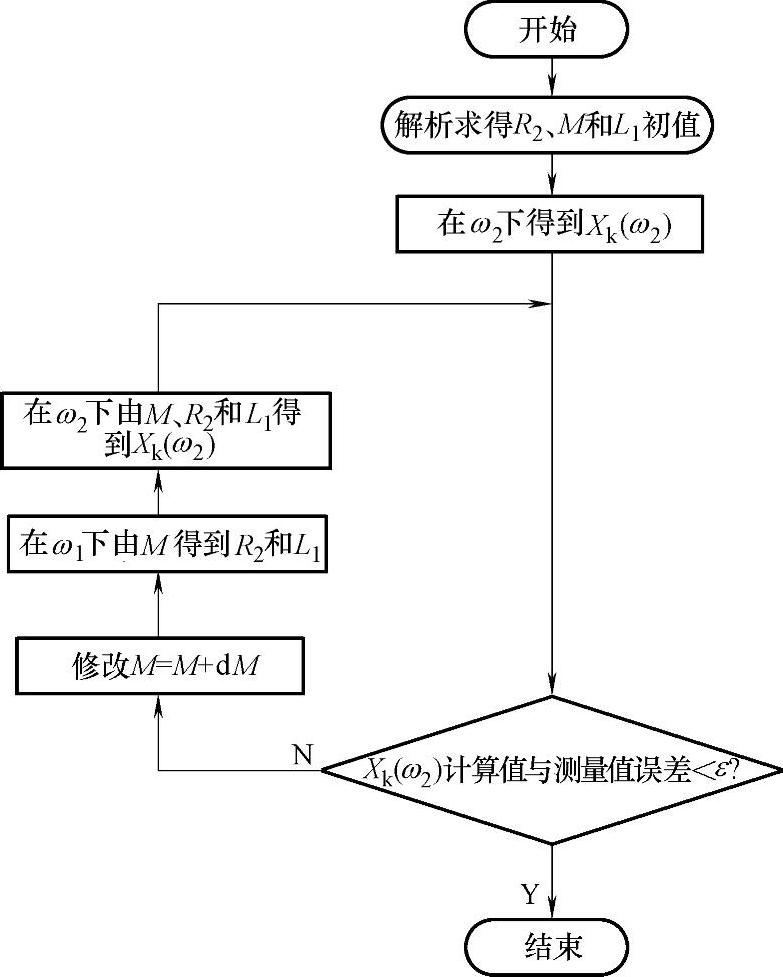
图4-11 参数辨识流程图

本节对电机旋转和静止两种条件下的参数辨识进行了实现，并在一台30kW电机上进行了实验对比，结果见表4-1。可以看出，两种方法的辨识结果比较接近，差别在5%以内，属于工程上可以接受的范围。需要指出的是，采用电机旋转的方法不存在收敛性问题，但由于需要电机旋转到接近同步转速，对于较大功率的电机来说，起动时间较长，相应的参数整定时间也比较长。而电机在静止条件下的参数辨识方法，由于不需要电机旋转到同步转速，参数整定时间较短，尤为适用于一些电机无法和负载脱离的场合。但是由于其本质上是要解一个非线性方程组，采用迭代方法时有可能造成结果不收敛，这是这种方法的缺点。

表4-1 30kW电机的参数辨识结果对比