SHEPWM属于优化PWM，又称开关点预置PWM。通过器件开关时刻的优化选择，可以直接控制基波和谐波的幅值。其主要优点是^[15]：①消除低次谐波，减少电流和转矩脉动；②在同样开关次数下，输出波形质量高，降低对输出滤波器的要求；③在同样波形质量下，其开关频率最低，开关损耗小，适合大功率场合；④直流母线电压利用率最高达1.15（折合成线电压近似为1）。缺点是需要事先大量的计算，存储数据量大，改动困难，不灵活。自1973年^[51]首次提出之后，得到了广泛的研究和应用，尤其适合于对开关频率有限制的高压大功率场合。三电平SHEP-WM在实际应用中的一个主要难点是非线性方程组的求解，具体到高压大容量变频器的应用，所求出的解还必须满足最小脉宽等问题。本节对三电平SHEPWM进行了深入研究，提出了一种新型求解公式，在1/4周期对称和1/2周期对称条件下发现了SHEPWM的多组解现象并对其规律进行了总结^[52，53]，最后还对三电平SHEP-WM在高压大容量中的应用进行了研究，包括最小脉宽问题、三电平SHEPWM和SVPWM的混合调制^[13]等。

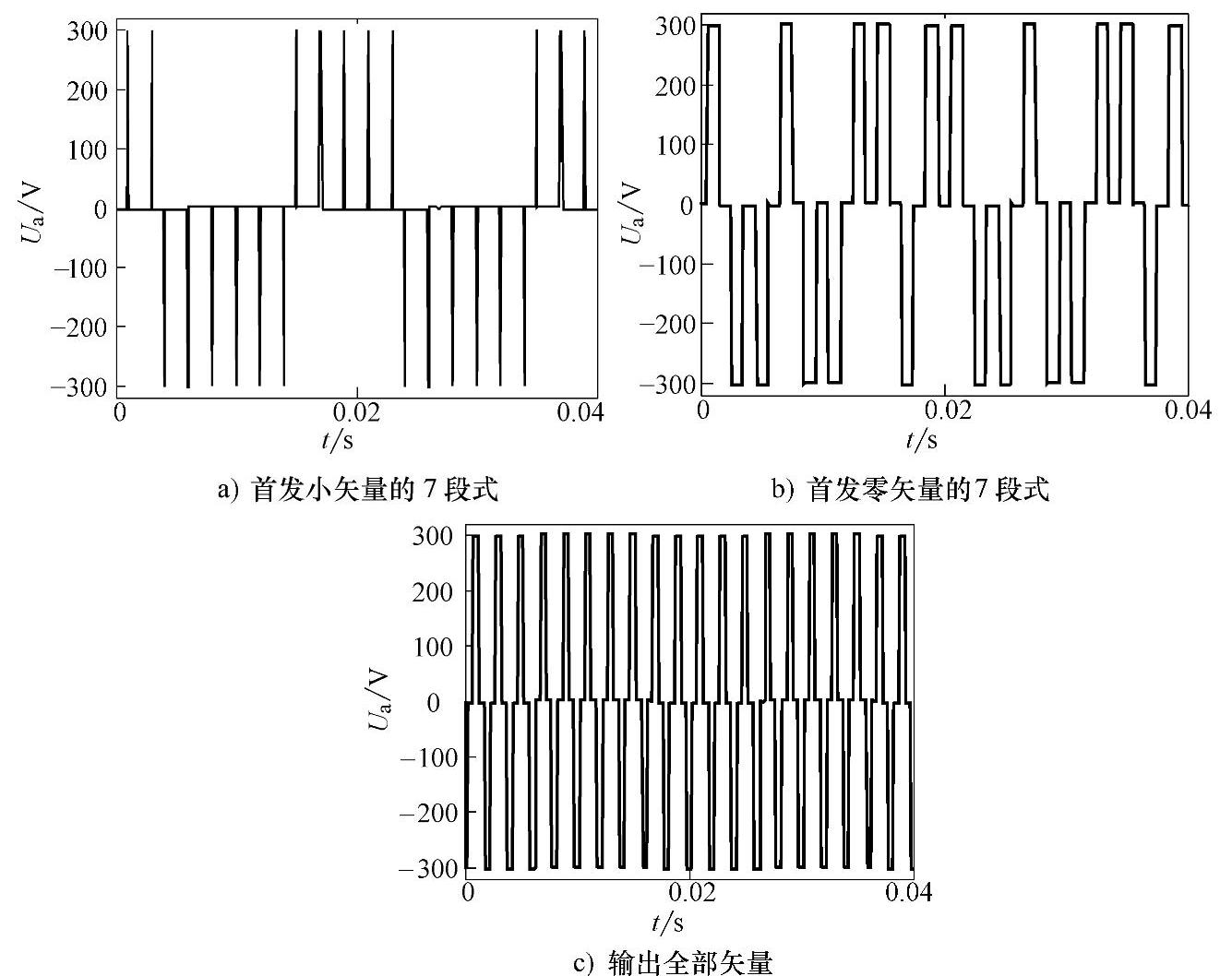
图3-17 m=0.05时的三电平相电压波形

1.1/4周期对称SHEPWM

（1）基本原理

为了简化SHE非线性方程组的求解，通常假设输出波形具有1/4周期对称性，即关于π/2偶对称，关于π奇对称，如图3-18所示。

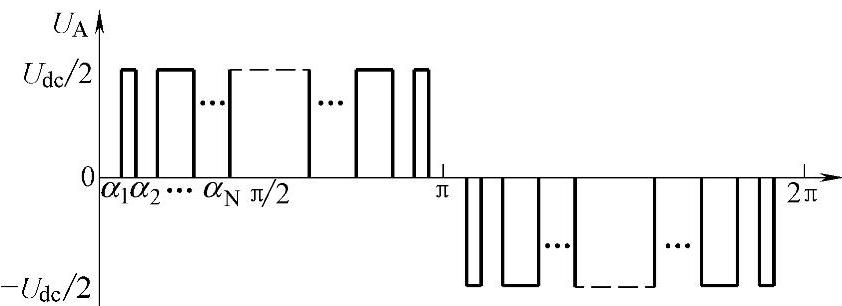
图3-18 三电平SHEPWM相电压波形

由函数奇偶性可知相电压波形中只含奇数次正弦分量，展开成傅里叶级数为

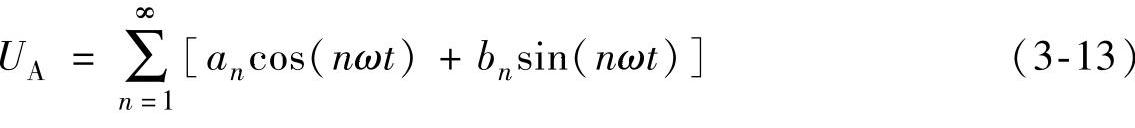
式中

a_n=0（所有n）

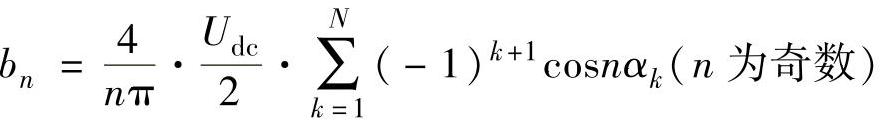
定义调制比为逆变器输出相电压基波幅值与半边直流母线电压的比值，即

m=b₁/（U_dc/2）

N个开关角度构成N个独立的方程，可以消除N-1个谐波分量。考虑到三相的对称性，3的倍数次谐波在线电压中自动消除，因此可以只消除非3倍数的奇次谐波。写成方程组为

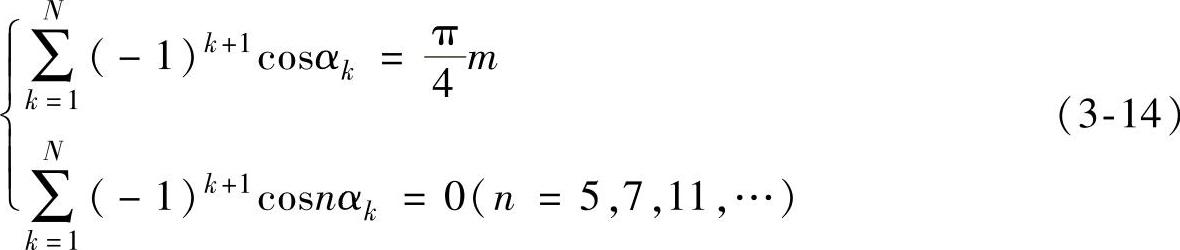
式中，0＜α₁＜α₂＜…＜α_N＜π/2。N为奇数时，n最大可以取到3N-2；N为偶数时，n最大可以取到3N-1。式（3-44）所示的方程组构造了在1/4周期内用N个开关角度来消除N-1个特定谐波的特定消谐技术的数学模型。

（2）SHEPWM方程组求解

SHEPWM方程组是一个非线性超越方程组，其求解过程中初值的选择十分重要，合适的初值可以使迭代的收敛速度大大加快，否则会迭代很慢甚至发散。各国学者对SHEPWM方程组初值的选择进行了大量研究，提出了各种各样的方法。参考文献[54～56]给出了调制比m=0时的初值解经验公式，利用SHEPWM方程组的连续可微性通过迭代可以得出调制比变大时的解。参考文献[15]提出以三角载波法生成非线性方程组初值的方法，使得求解非线性方程组的速度明显加快。为了扩大初值选择的范围，减少对初值选择的依赖性，也有采用其他方法如神经网络^[57]、Walsh变换^[58]和同伦算法^[59-60]等来求解SHEPWM方程组。尽管各国学者提出了不同的方法，在一定程度上加快了方程求解的收敛速度，但距真正实现在线求解还有一定距离。目前在实际中应用的还是先离线求解并把结果存于存储器，然后通过微处理器查表实现^[61]。

式（3-14）是一个非线性超越方程组，其求解难度直接制约着SHE在实际中的应用。通常需要采用数值算法通过迭代进行求解，其中初值的选择又直接影响着迭代的收敛性，因此问题转化为如何得出比较好的初始值。由于方程组（3-14）中的各项连续可微，说明其解轨迹也是连续的。这里给出一个初值解经验公式，在其基础上可以快速得出m=0的解，然后给m一个很小的增量dm，采用牛顿迭代法可以很快得到新解，如此逐步增大m，可以得到m全范围内的解。

参考文献[54]给出了一组三电平SHE的初值经验公式，见式（3-15）。本节通过大量的实验，总结出另外一组初值解经验公式^[52]，见式（3-16）。由于N为偶数时最大调制比变化较大，而N为奇数时最大调制比基本上稳定在1.15，这里只研究N为奇数的情况。式（3-15）和式（3-16）所示两组经验公式均假设N为奇数。

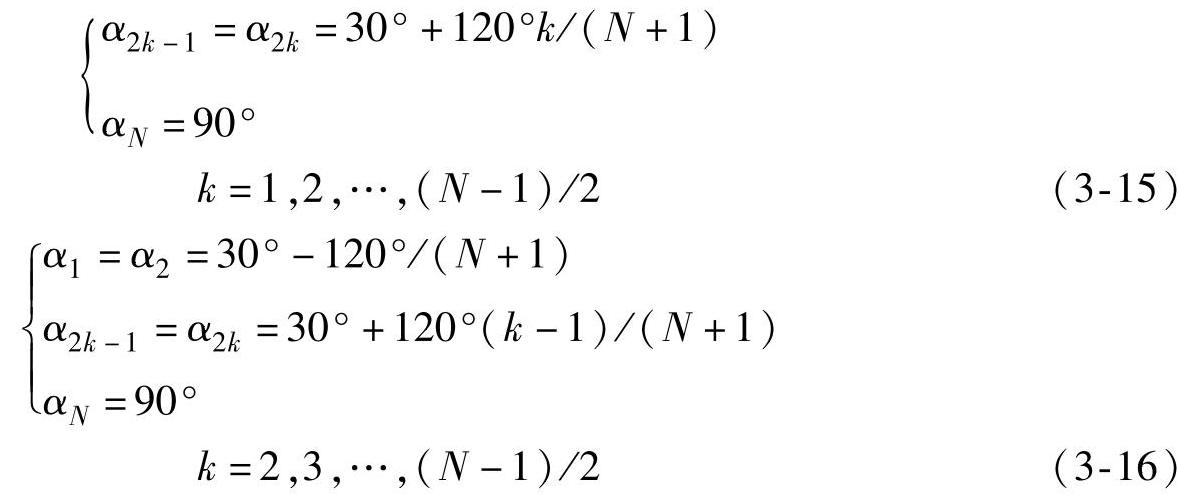
图3-19所示是采用式（3-15）所示经验公式时N=7、13、21和25时的解轨迹。

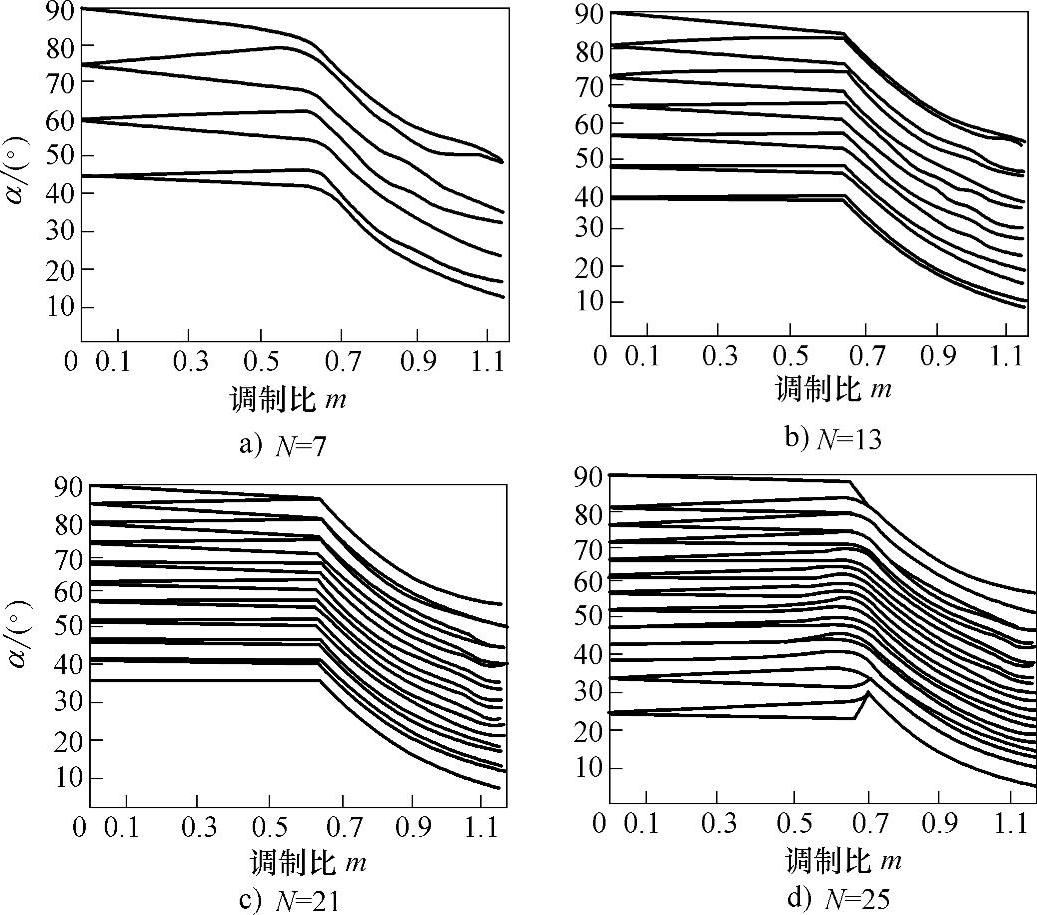
图3-19 第1组解轨迹图

图3-20所示是采用第2组经验公式（3-16）时N=7、13、21和25时的解轨迹。

实际计算结果表明，式（3-15）和式（3-16）所示初值解经验公式在收敛性方面有所不同。第1组初值解在整个调制比范围内收敛，观察图3-19所示解轨迹可以发现在m=0.65处解轨迹的走向发生变化，是一个转折点。第2组初值解在调制比小于0.65时可以快速收敛，但在m=0.65左右发生跳变，在此处解轨迹发生分岔现象。也就是说，采用第2组初值解，在m=0.65处，采用不同的数值算法，可能会导致不同的解轨迹，其原因是SHEPWM非线性方程组的多解性。图3-21所示为高调制比时N=7的四组解轨迹。其中，解2轨迹和采用第1组初值解时的解轨迹相同。

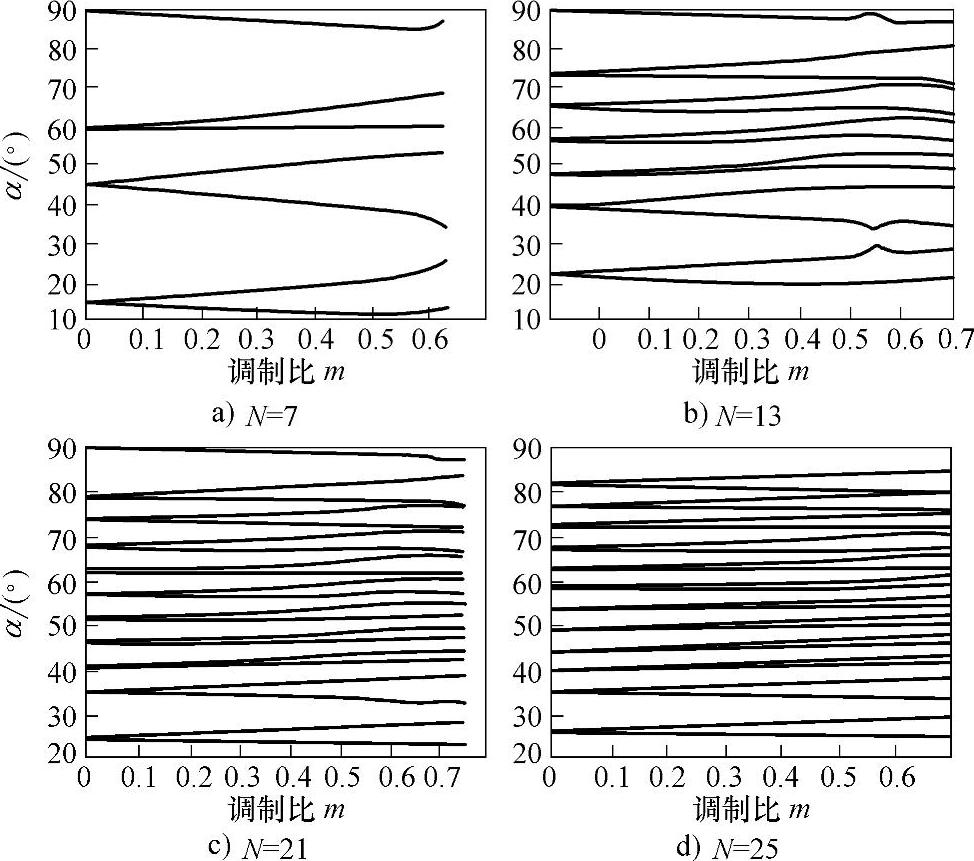
图3-20 第2组解轨迹图

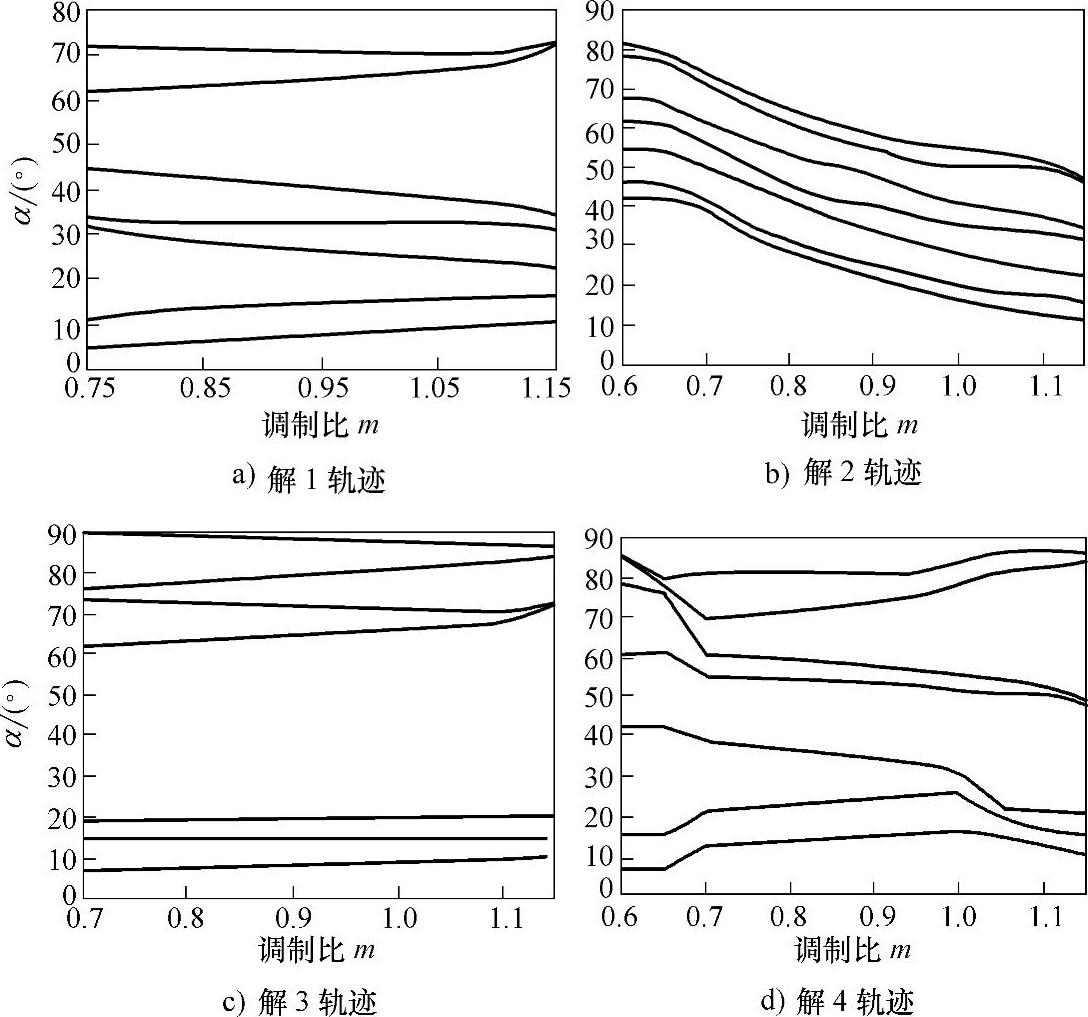
图3-21 高调制比时的四组解轨迹图（N=7）

表3-2是开关点数N=7，调制比m=1.04时的四组解。为了形象直观地看出四组解在脉冲上的区别，图3-22给出了四组解所对应的一相单管脉冲，从上至下分别对应第1组～第4组解。可以看出，解1和解4的脉冲宽度分布要比解2和解3相对均匀一些。实际应用时，可以根据器件的开关频率和对最小脉宽的要求进行选择。

表3-2 四组开关角度解

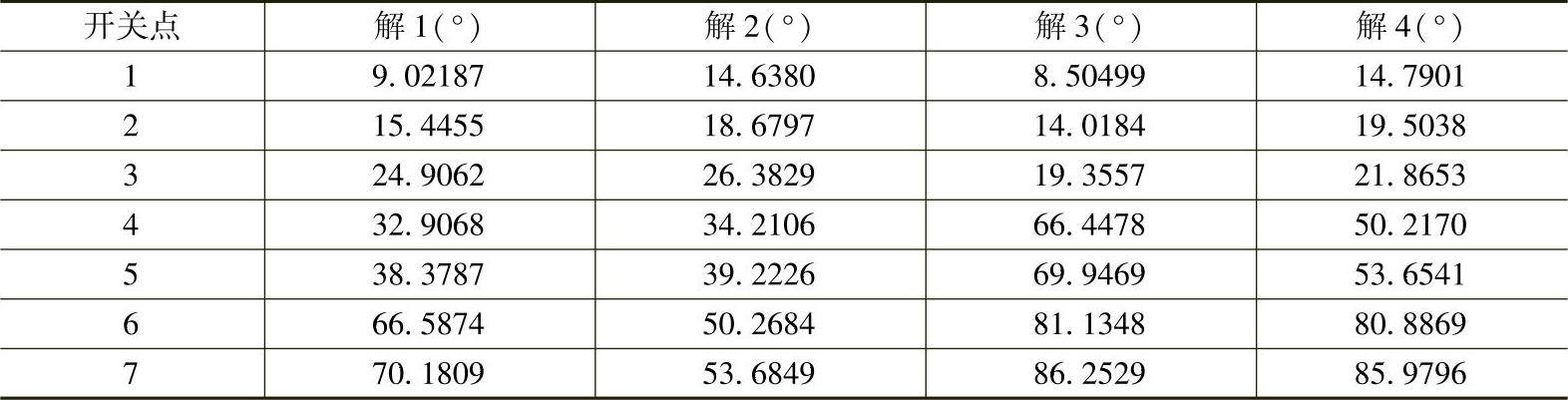
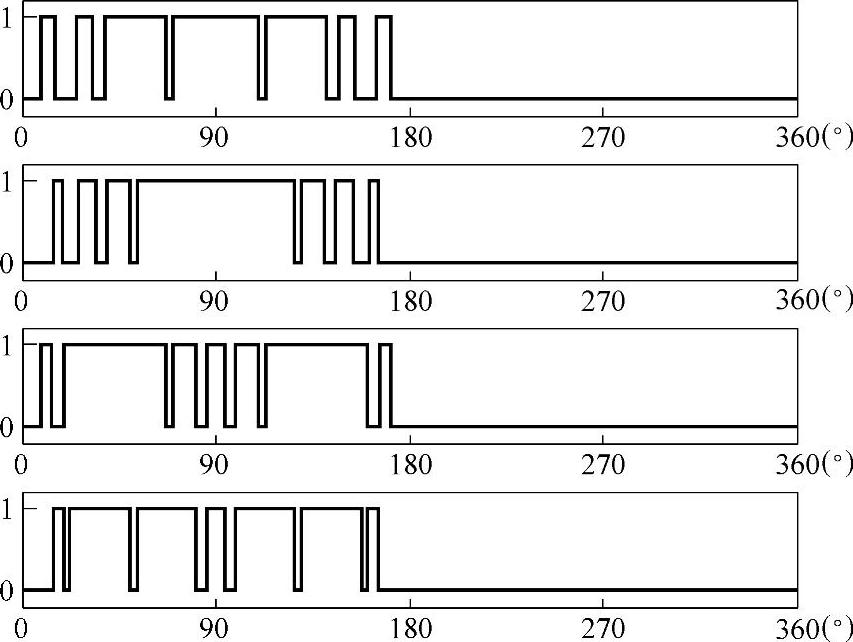
图3-22 四组解所对应的一相单管脉冲（N=7）

（3）SHEPWM仿真研究

图3-23给出了表3-2中四组解的线电压输出仿真波形及其谐波比较。

表3-3给出了四组解对应的THD比较。

表3-3 四组解对应的THD比较

图3-24以N=9为例给出了考虑死区和不考虑死区时的频谱。可见，当加入死区后，会产生一些低次谐波。

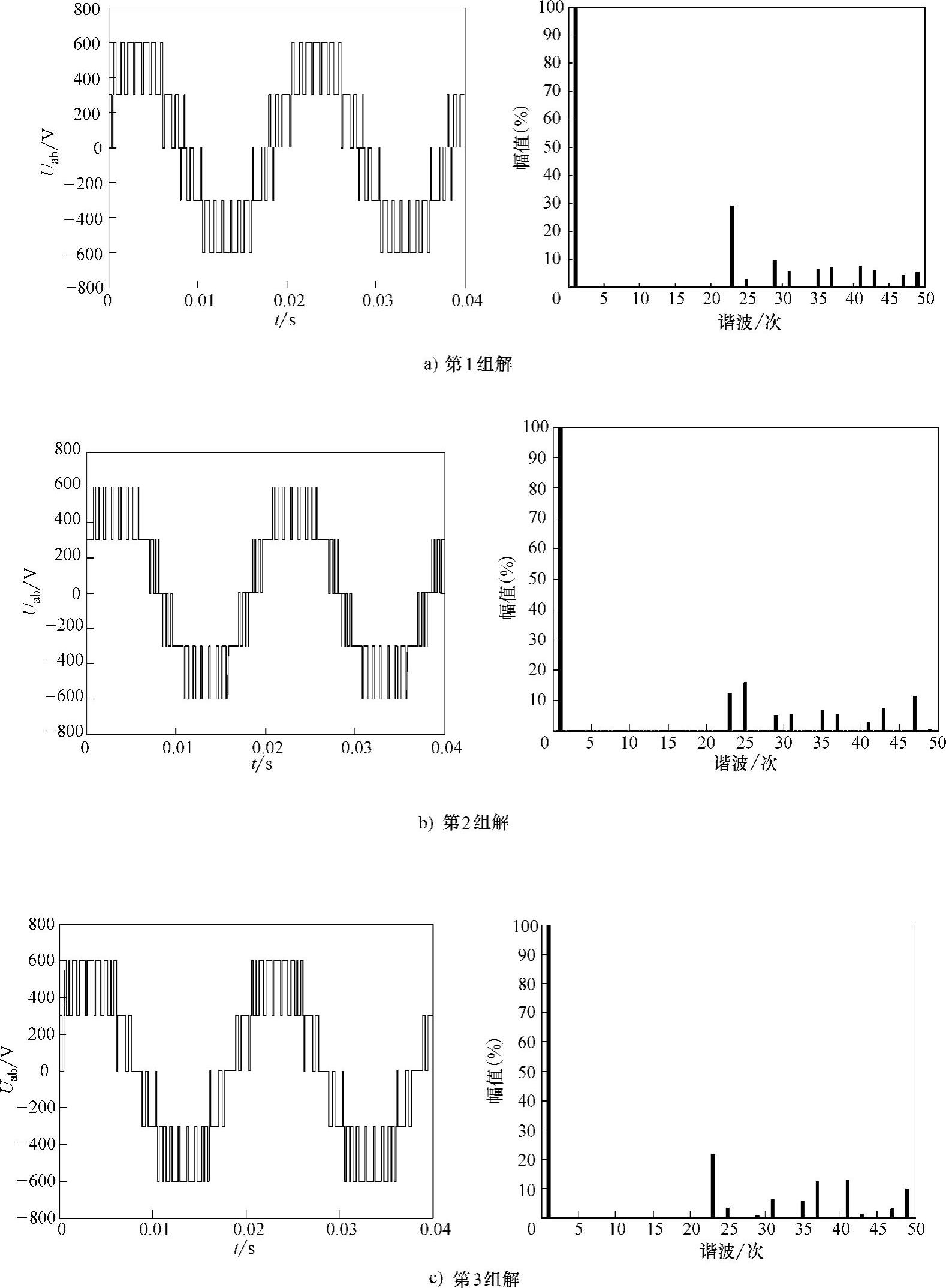
图3-23 四组解线电压及其频谱

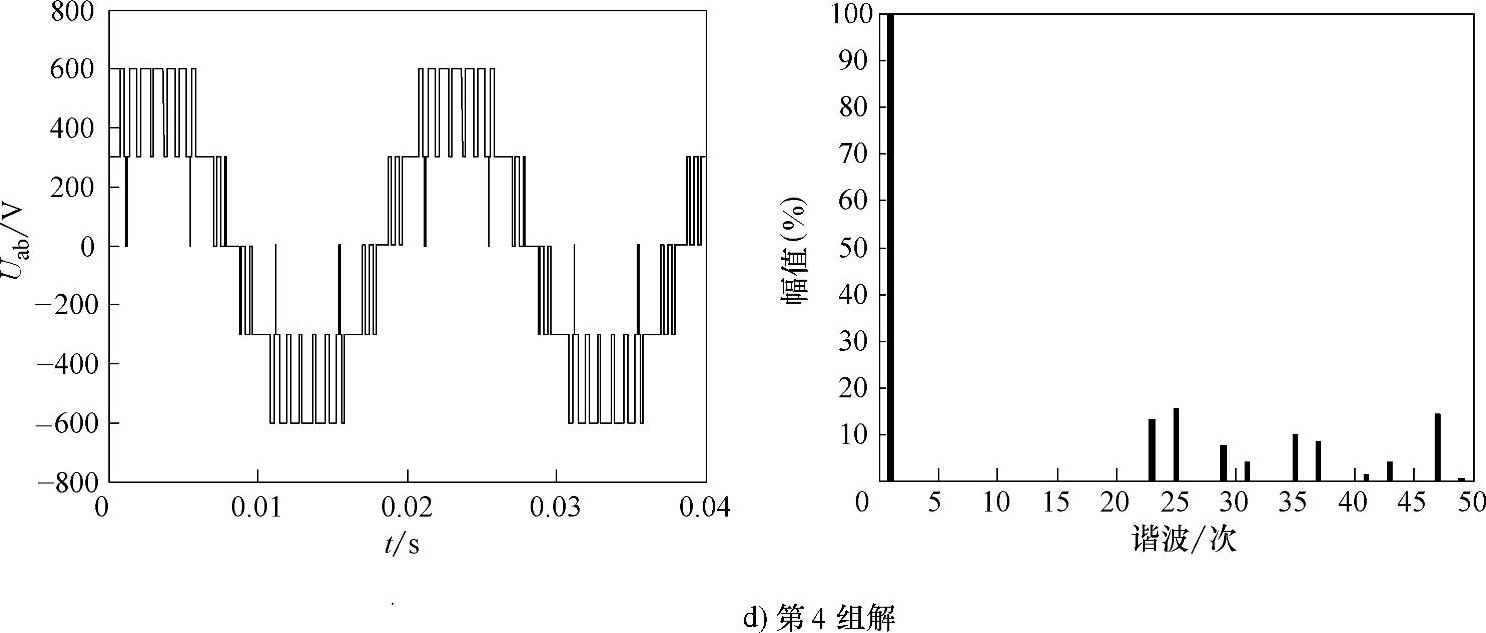
图3-23 四组解线电压及其频谱（续）

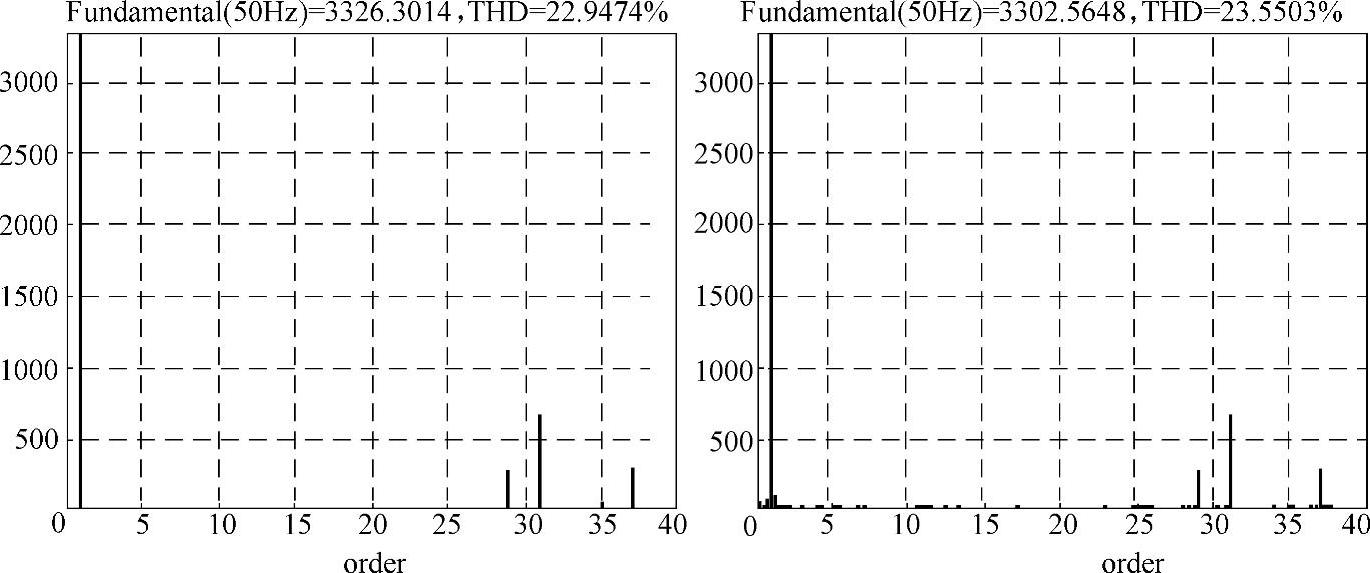
图3-24 有无死区仿真结果比较

分析以上结果可知，不同解对应的THD可能不一样，但都能够消除指定的低次谐波。

（4）实验结果

为验证这里所提出的方法，在55kW三电平NPC逆变器上进行了实验。开关器件为IGBT，调制比m=1.04，N=7，基波频率=50Hz。图3-25和图3-26所示是逆变器输出线电压波形及其频谱。从中可以看出，四组解都达到了消除25次以下低次谐波的效果，证明了四组解的正确性。图中在低频时出现的一些幅值极低的低次谐波，是由于死区所引起。

表3-4给出了计算到50次谐波时四组解所对应的THD和总的谐波畸变率（Total Distortion Ratio，TDR）。可见四组解虽然同样达到消谐的目的，但剩余高次谐波的含量却是不一样的，从而为实际中应用SHEPWM时提供了更多的选择。

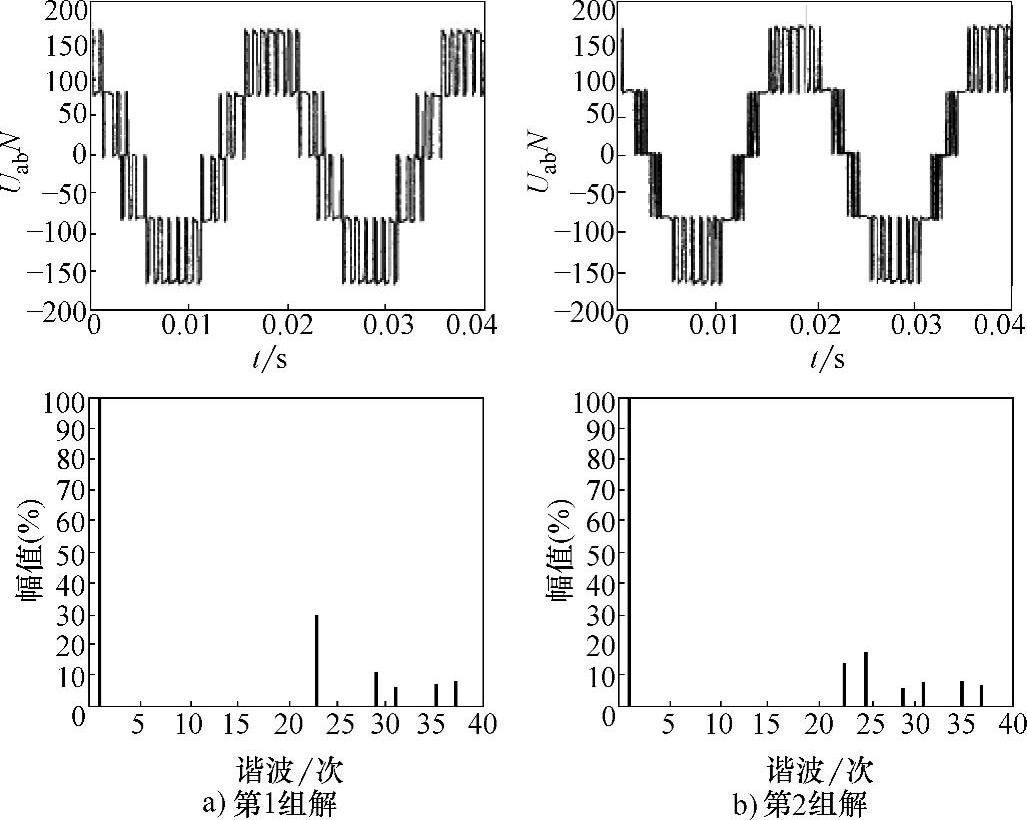
图3-25 线电压波形及频谱（第1、2组解）

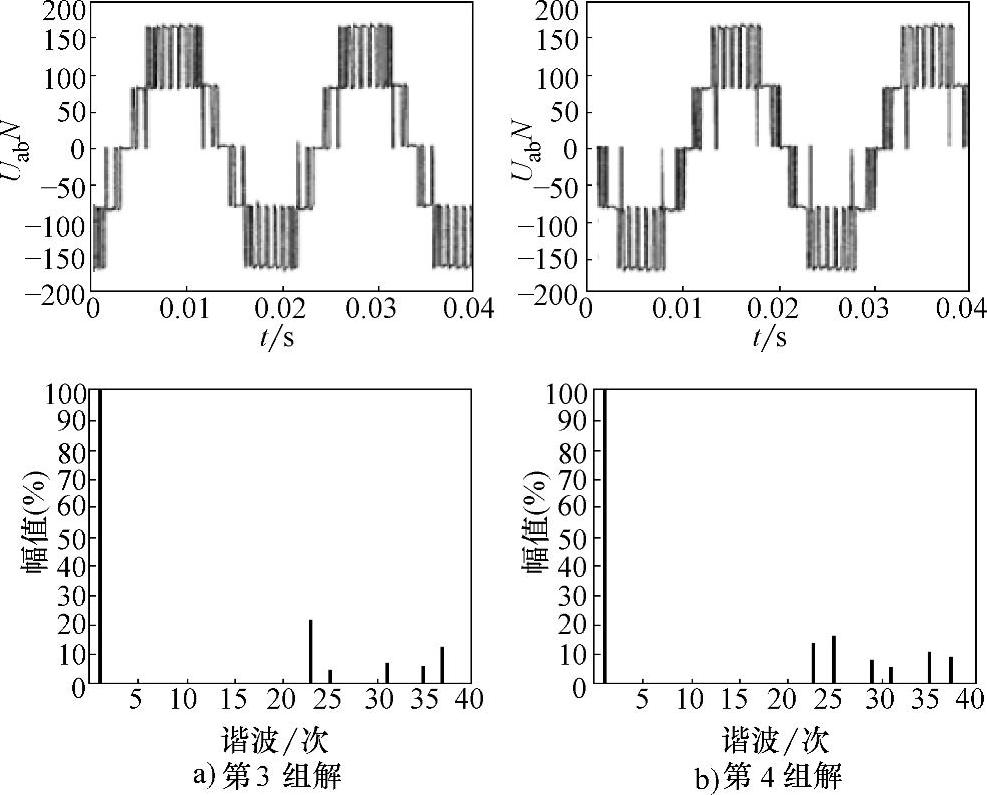
图3-26 线电压波形及频谱（第3、4组解）

表3-4 四组解所对应的谐波畸变率

2.1/2周期对称SHEPWM

目前关于SHEPWM的研究，无论两电平还是多电平，均假设输出波形是1/4周期对称^[52，54-63]。这有利于简化非线性方程组的维数，但同时也减少了解空间，得到的可能不是最优解。事实上，1/4周期对称并不是SHEPWM必须满足的条件，采用1/2周期对称可以达到同样的消谐效果，而且由于求解空间变大，可以得到更多解甚至无数组解。这里首先针对1/4周期对称SHEPWM，以N=7为例给出了四组解，然后进一步研究了1/2周期对称下SHEPWM方程组的解，得出了两种类型的解，指出了其与1/4周期对称的解的联系和不同。最后在实际三电平NPC逆变器上验证了这里所给解的正确性。

（1）基本原理

从对称性来看，只要相电压波形具有原点奇对称和1/2周期对称（关于π负奇对称）就可以保证输出波形只含奇数次正弦分量。对于三相对称输出系统，3的倍数次谐波在线电压中自动抵消，消谐时可以只消掉非3倍数的奇数次谐波。通常文献中假设波形具有1/4周期对称性（关于π/2偶对称）可以减少非线性方程组的维数，从而有利于方程组的求解。但这样在简化方程组的同时，也减少了可行解的空间。图3-27给出了相电压只具有1/2周期对称性和同时具有1/2和1/4周期对称性时的波形。图3-27a和图3-27b在半周期内具有相同的脉冲个数，设为N，分别对应N个开关角度和2N个开关角度，可以在控制基波的同时，消除N-1个谐波分量。

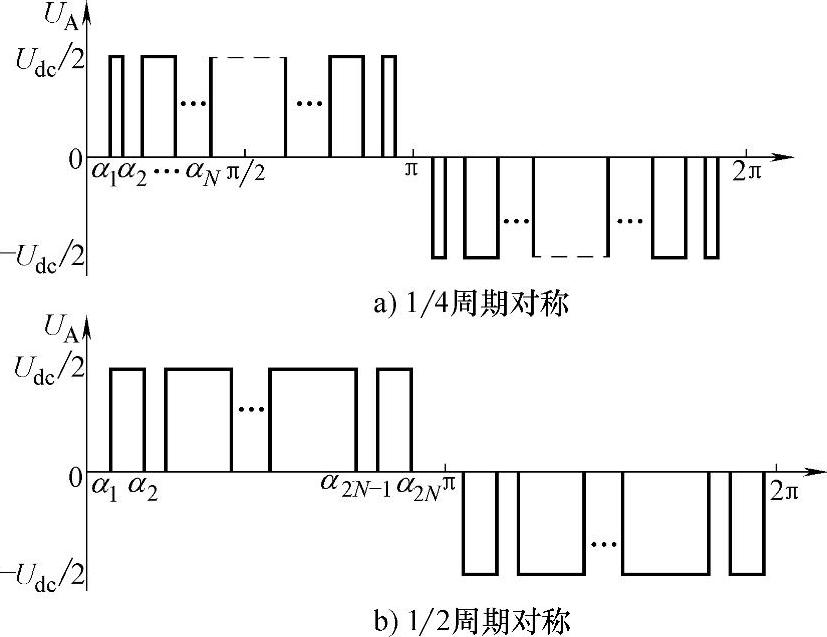
图3-27 三电平SHEPWM相电压波形

对图3-27b中相电压进行傅里叶分解，可得

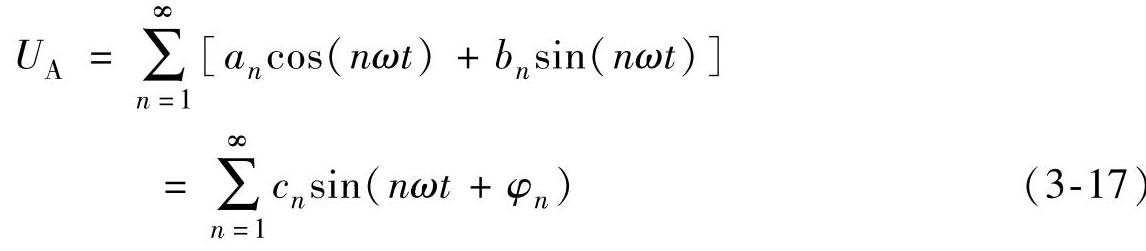
式中

定义调制比为逆变器输出相电压基波幅值与半边直流母线电压的比值，即

m=c₁/（U_dc/2）(www.daowen.com)

考虑三相对称输出的情况，消掉N-1个非3倍数的奇次谐波，得到式（3-19）所示方程组：

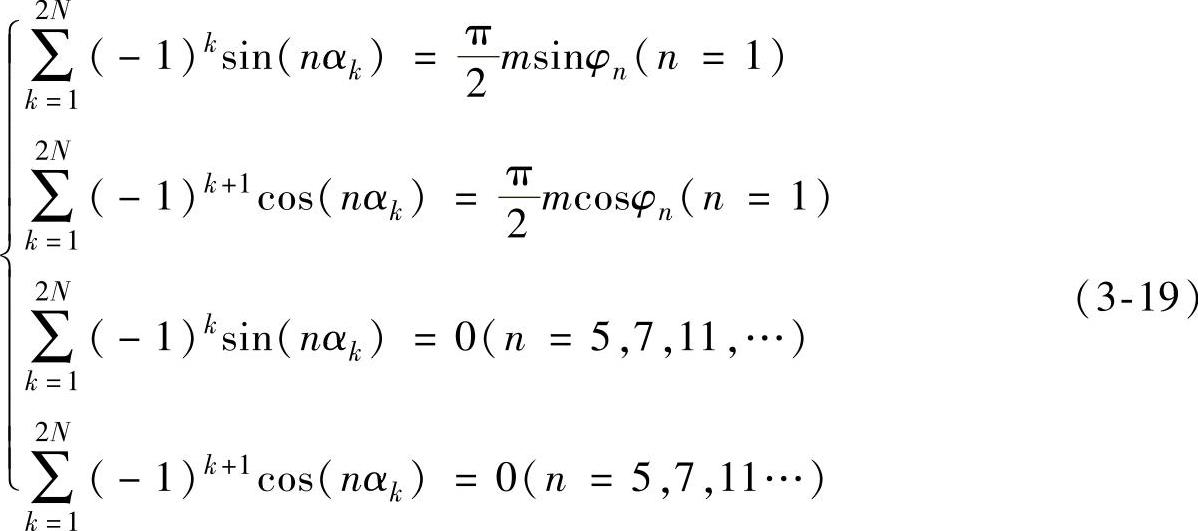
式中 0＜α₁＜α₂＜…＜α_2N-1＜α_2N＜π。N为奇数时，n最大可以取到3N-2；N为偶数时，n最大可以取到3N-1。

下面指出1/4周期对称SHEPWM与1/2周期对称SHEPWM的区别。在1/4周期对称SHEPWM中，由于α₁，α₂，…，α_N与α_N+1，α_N+2，…，α_2N关于π/2对称，即α_k=π-α_2N+1-k（k=1，2，…，N），且sin（nαk）与sin（nα_2N+1-k）在式（3-18）中的符号相反，所以a_n=0。这意味着相电压中只含正弦分量，且所有奇次谐波和基波要么同相位，要么反相位，取决于b_n的符号。这是1/4周期对称SHEPWM能够简化方程的原因。相应的，式（3-19）所示方程组简化为式（3-20），其中0＜α₁＜α₂＜…＜α_N＜π/2。

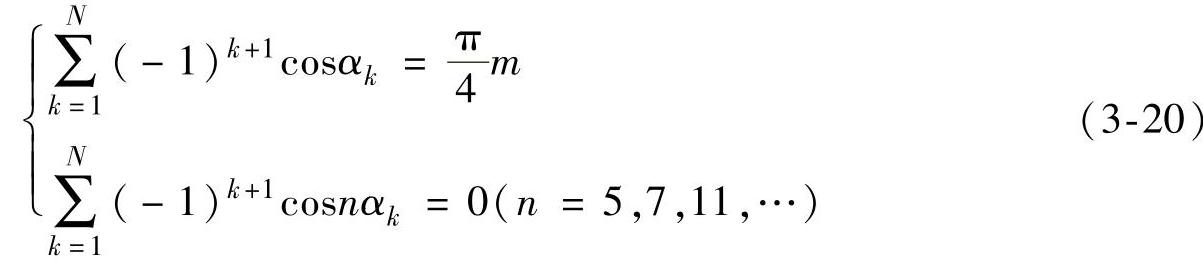
可见，1/4周期对称SHEPWM只是1/2周期对称SHEPWM的一个特例，在1/2周期对称下考察SHEPWM更全面，可以得到更多的解。式（3-19）所示的方程组构造了在1/2周期内用2N个开关角度来消除N-1个特定谐波的数学模型，含有2N个自变量，比消除同样谐波次数的1/4周期对称SHEPWM的方程个数要多一倍，但开关次数是一样的。特定消谐技术只要求消除低次谐波，并不一定要求基波的相位φ₁=0，从而为方程组增加了一个自由变量，而1/4周期对称SHEPWM隐含了基波的相位φ₁=0，这是两者的不同之处。

（2）SHEPWM方程组求解

1/2周期对称SHEPWM和1/4周期对称SHEPWM在方程组求解上可以采用相同的方法，满足后者的解同样也满足前者。式（3-19）所示的非线性方程组通常需要采用数值算法通过迭代进行求解，其中初值的选择又直接影响着迭代的收敛性。参考文献[54]给出了调制比m=0时的初值经验公式，还有文献采用正弦波调制^[56]和梯形调制^[64]来得到初始解。另外，还可以采用预测初始值^[55]、牛顿迭代和同伦算法相结合^[59-60]等数值算法。事实上，可以采用上述任何一种数值算法来进行求解，这里采用通常的牛顿-拉夫逊迭代法来进行求解。本节关心的重点是满足1/2周期对称SHEPWM的解的特性，因此这里对如何求解SHEPWM方程组不再详述。

（3）SHEPWM方程组两种类型的解

由于1/2周期对称SHEPWM比1/4周期对称SHEPWM多了一个自由度即基波相位，以满足后者的解为初值，通过调整基波相位可以得到一组新解，称为解类型Ⅰ，它的各个解分量不再是关于π/2对称；还有一种类型的解和1/4周期对称SHEPWM的解没有关系，它的各个解分量相互独立，不存在对称性的关系，称为解类型Ⅱ。下面对两种不同类型的解进行分析，重点比较其谐波特性。

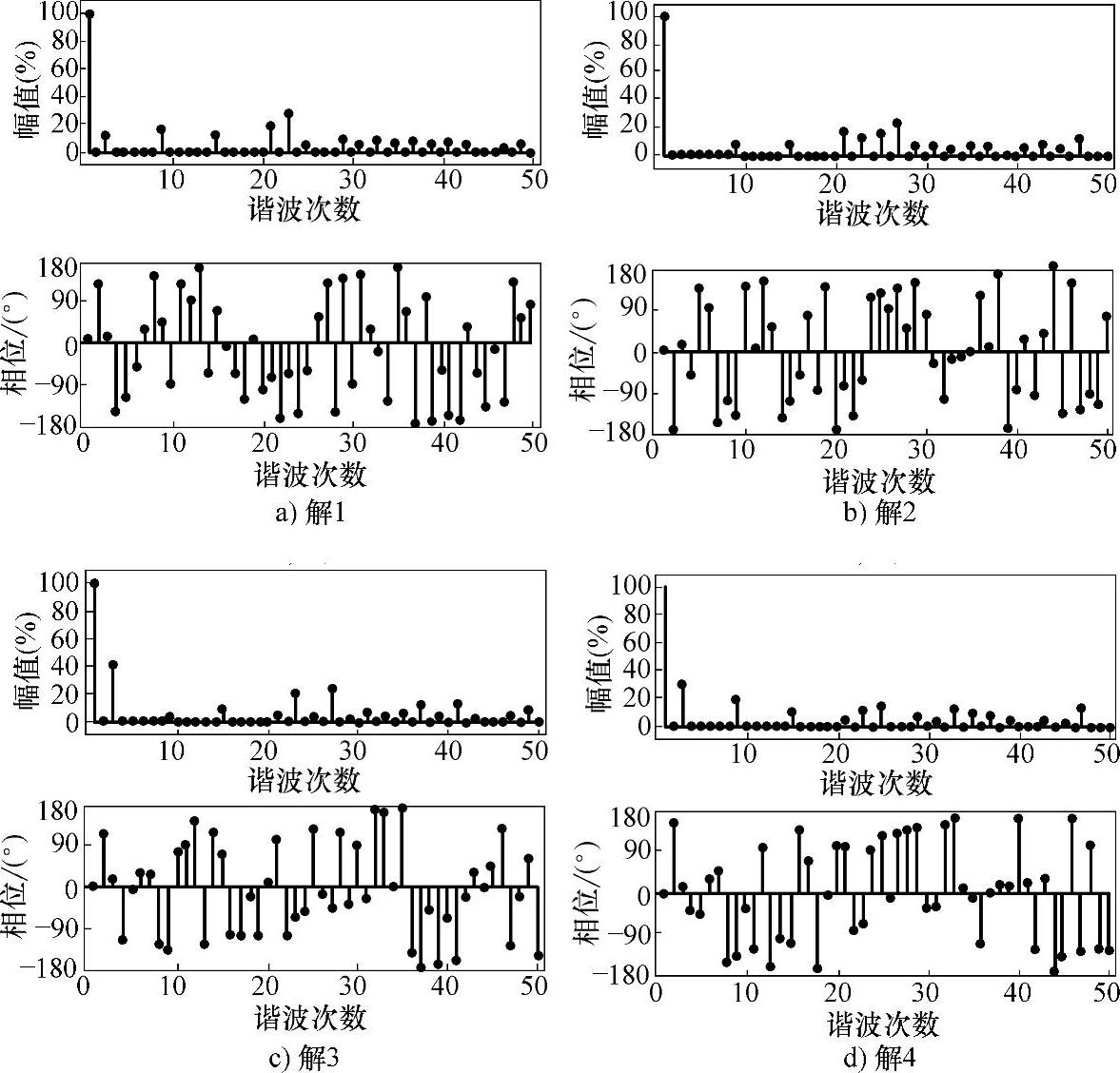
图3-28 四组1/2周期解类型Ⅰ的频谱（φ₁=5°）

表3-2给出了开关点数N=7，调制比m=1.04，基波频率为50Hz时1/4周期对称SHEPWM方程组的四组解。以表3-2所示的解为基础，通过调整相位可以得到一组新解，属于解类型Ⅰ。表3-5所示为基波相位φ₁=5°时的新解。比较表3-2和表3-5可以发现，基波相位偏移5°，相应的开关角度解也偏移5°，但谐波的相位偏移则不同。图3-28给出了表3-5四组解所对应谐波的幅值和相位。可以发现四组解都达到了消除低次谐波的目的，但谐波的相位却不相同。通过表3-2和表3-5可以总结出规律：将1/4周期对称SHE的解增加或减少一个角度，则相应的基波也左移或右移同样的角度。需要注意的是，必须保证平移后开关角度解仍然在0～360°范围内。这就从理论上说明了在1/2周期对称下，可以得到无数组解。

表3-5 四组1/2周期对称解（解类型Ⅰ）

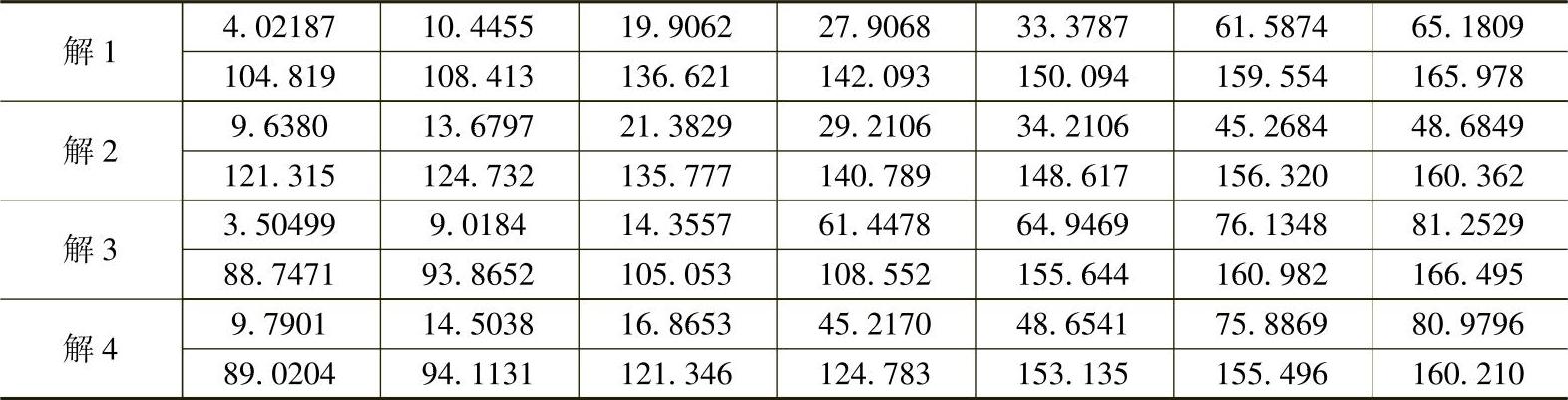
类型Ⅱ不存在类似解类型Ⅰ那样的对称性，从图3-29所示的单管脉冲可以形象直观地看出。表3-6给出了两组1/2周期对称解，图3-30所示为其相应的幅值和相位信息。类似解类型Ⅰ和1/4周期对称解的关系，当基波相位偏移5°时可以得到另外一组解，新解的开关角度相比原来的解也是偏移了5°。相应的频谱见图3-31。

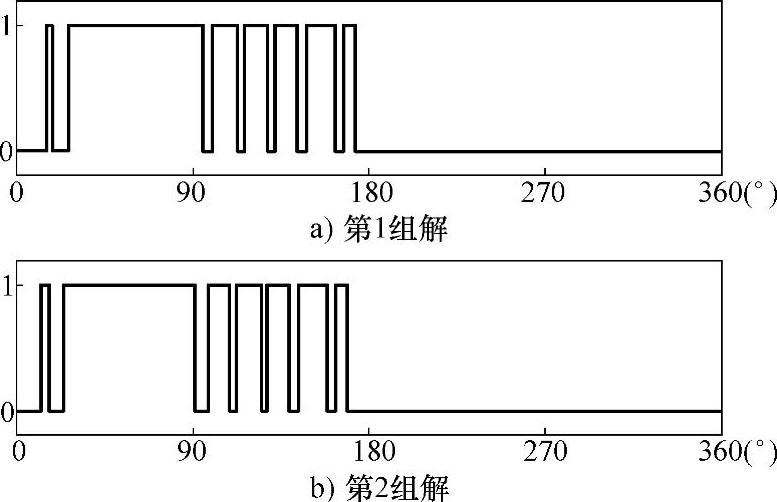
图3-29 两组1/2周期解类型Ⅱ所对应的单管脉冲

表3-6 两组1/2周期对称解（解类型Ⅱ）

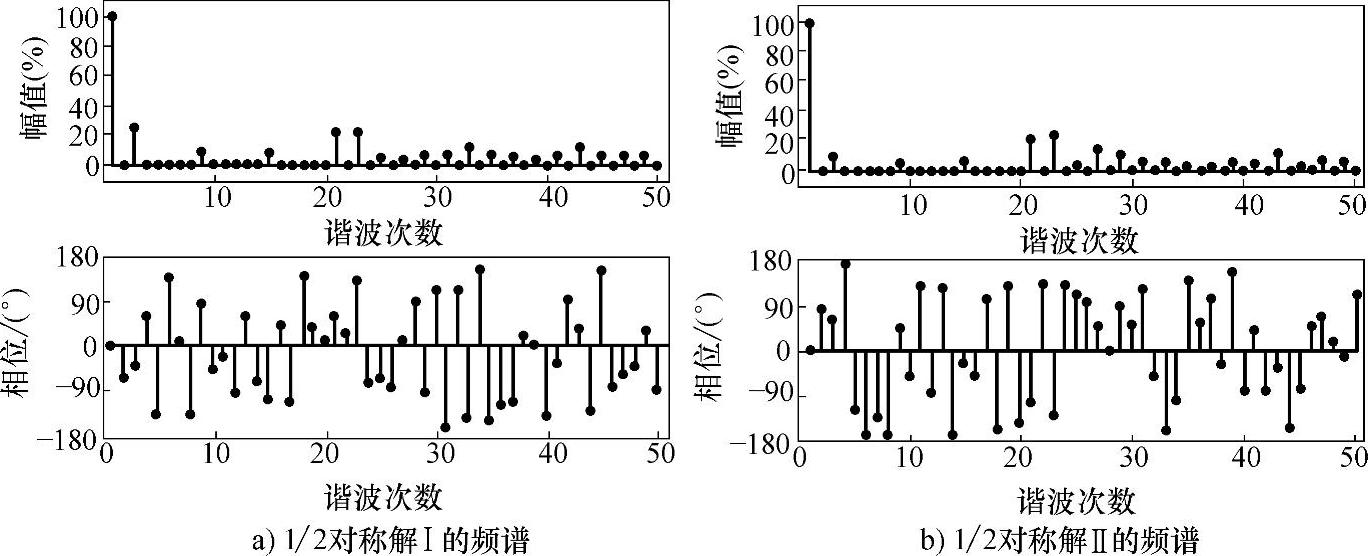
图3-30 两组1/2周期解类型Ⅱ的频谱（φ₁=0°）

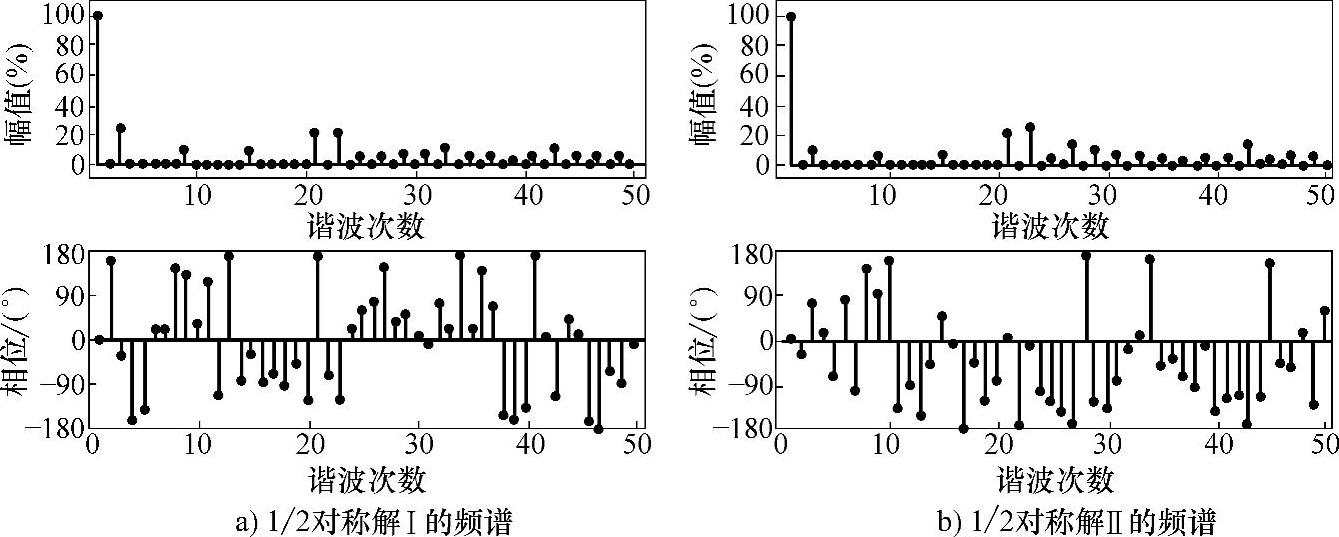
图3-31 两组1/2周期解类型Ⅱ的频谱（φ₁=5°）

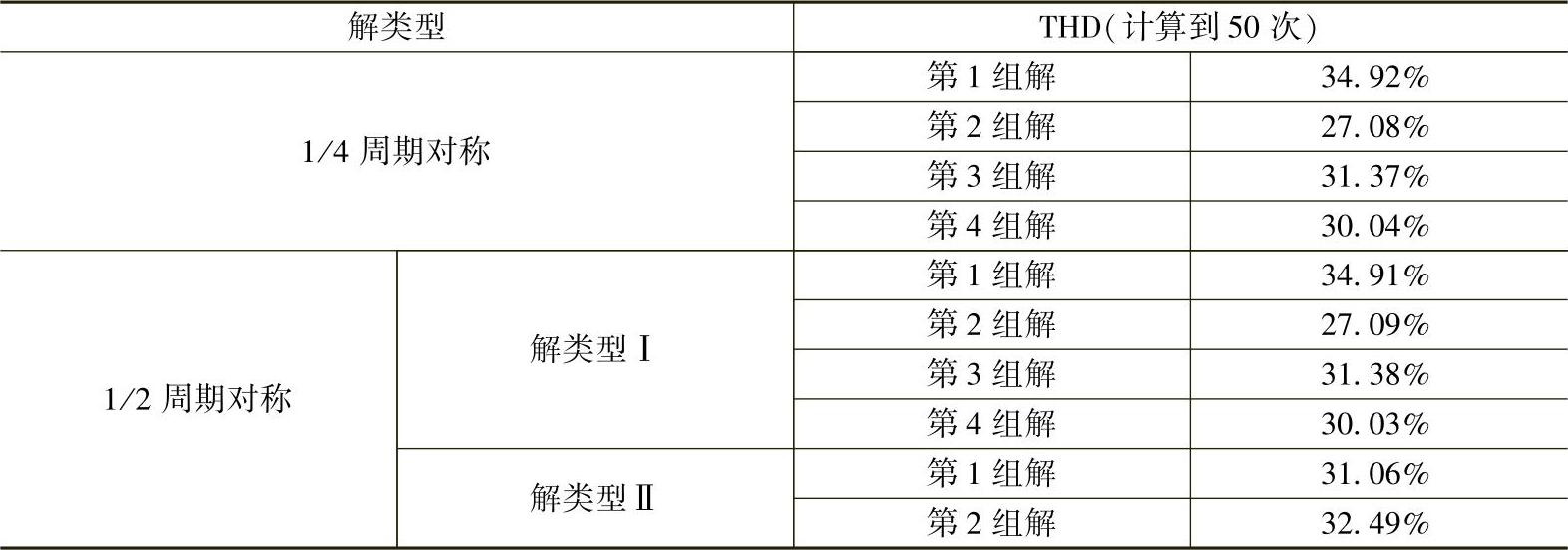
表3-7给出了1/4周期对称解和1/2周期对称解的THD，谐波计算到50次。需要指出的是，对于1/2周期对称的解类型Ⅰ，其四组解所对应的THD和1/4周期对称的四组解基本相同，即仅有基波相位变化产生的新解和原来的解相比各次谐波幅值变化不大，但相位发生了变化。

表3-7 不同解的THD

（4）实验结果

为验证这里所给出的不同类型的解，在三电平NPC逆变器上进行了实验研究。实验条件为调制比m=1.04，N=7，基波频率=50Hz。图3-32所示是1/2周期对称时解类型Ⅰ的四组解所对应的线电压波形及其频谱，图3-33所示是解类型Ⅱ时的两组解所对应的线电压波形及其频谱。可以看到25次以下谐波均被消除，从而证明了这些解的正确性。另外需要说明的是，这里所给出的几组不同类型的解虽然都可以达到消除低次谐波的效果，但剩余高次谐波的含量却是不一样的，实际应用时可以根据需要选择。

3.三电平SHEPWM在高压大容量变频器中的应用

SVPWM将逆变器和电机看成一个整体，易于实现数字化控制，具有转矩脉动小、噪声低和电压利用率高等优点，目前被广泛用于变频调速中，但采用异步调制在高频时由于载波比变小，谐波特性变差。基于SVPWM和SHEPWM调制方式的优缺点，这里提出了一种应用于三电平NPC逆变器的混合调制方法：在低频时采用异步SVPWM调制，由于载波比较高，可以有效地抑制谐波，减少电流和转矩脉动，而且由于三电平NPC逆变器中存在冗余空间矢量、控制灵活、便于考虑中点平衡和最小脉宽等问题，容易针对起动施加额外的算法如预励磁控制^[65]等；在高频时采用特定消谐PWM，可以大大改善波形质量，而且由于需要消除的谐波次数较少，对存储量的要求较低，实现相对容易。混合调制可以使在整个频率范围内都有较好的谐波特性，其主要难点在于要保证不同PWM调制方法之间切换时的平滑过渡，否则电压可能会发生突变甚至振荡。这里分析了影响SVPWM和SHEPWM平滑切换的原因，并提出了具体的解决方法。通过PSIM软件对SVPWM和SHEP-

图3-32 1/2周期解类型Ⅰ四组解实验波形及频谱

WM进行了仿真研究，并在实际三电平变频器平台上进行了实验验证。

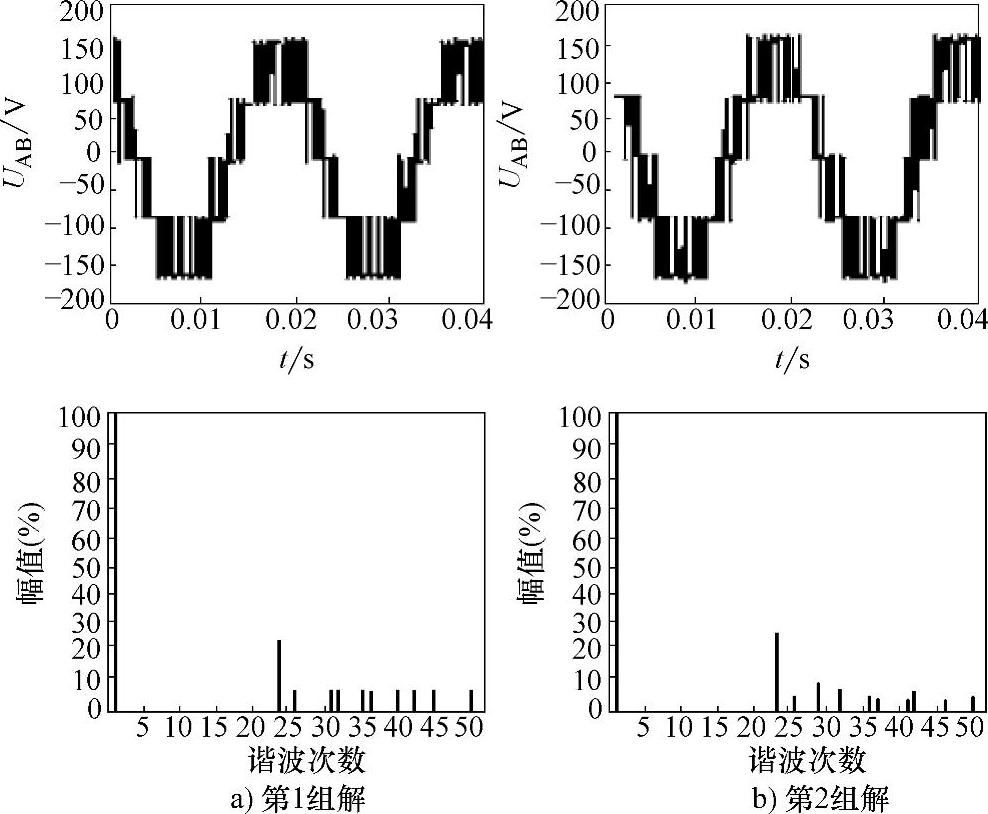
图3-33 1/2周期解类型Ⅱ两组解实验波形及频谱

（1）三电平SHEPWM解的选择

根据实际负载情况和现场要求，这里在小于45Hz时采用异步SVPWM，开关频率为600Hz，45Hz以上采用SHEPWM，开关点数取为7，可以消除相电压频率为1000Hz以内非3整数倍的低次谐波。三电平SVPWM的算法见3.3.3节。这里着重叙述三电平SHEPWM解的优化选择。由前面仿真结果可知，SHEPWM方程组存在多组解。这些解虽然都能消除同样的低次谐波，但管子所对应的脉冲宽窄和分布是不同的。在高压大容量中采用的电流型器件如GTO、IGCT等，由于存在最小开通和关断时间，通常对最小脉宽有较严格的限制，一般为至少几十微秒。为了保证其可靠工作，减少开关损耗，通常开关频率不超过1kHz。实际中需要对不同的解进行比较，以满足器件的工作要求。以表3-2中的解1和解2为例，其对应到开关器件上的脉冲波形如图3-34所示。

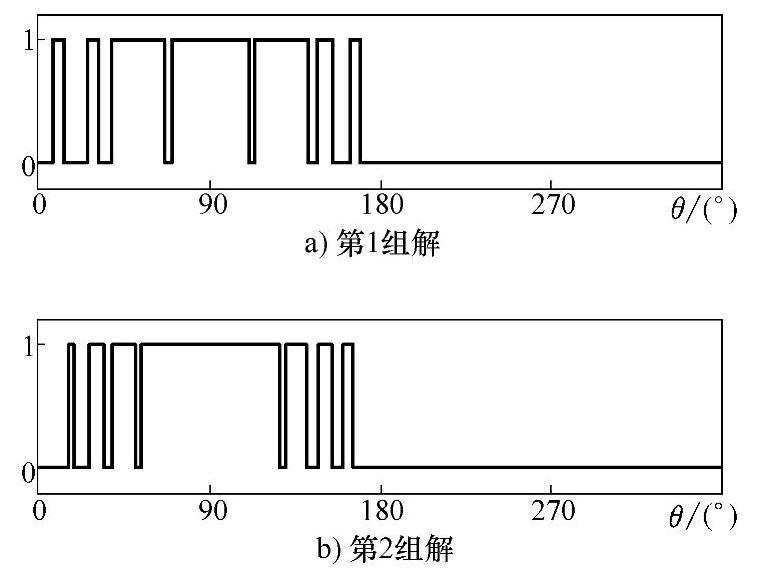
图3-34 三电平SHEPWM下的单管驱动脉冲

比较图3-34中两组解所对应的管子脉冲，可以发现第1组解对应的脉冲宽度更宽，更不容易受最小脉宽的影响，因此这里采用的就是第1组开关角度解。

（2）三电平SVPWM和SHEPWM的平滑切换

理论上，只要SVPWM结束时的参考矢量相位和SHEPWM的相位相同，就可以平滑切换。具体说明如下，设三相参考电压为

，，

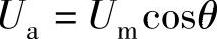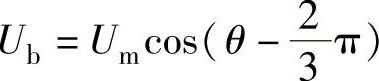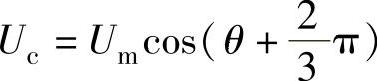
按空间矢量理论可得综合矢量为

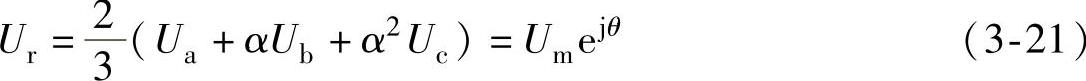
即SVPWM中给定参考电压矢量的相位就是A相电压的相位。实验时发现按照上面理论分析的结果并不能保证SVPWM和SHEPWM之间的平滑切换，而是在相位上有所偏差。分析其原因主要有下面几点：①死区和最小脉宽的影响使得最后实际发出的矢量和给定参考矢量在幅值和相位上有所偏差，尤其相位上；②SVPWM采用异步调制，开关频率固定，而SHEPWM属于同步调制，开关频率一直在变化，二者衔接时就有可能出现相位角度的跳跃；③前面的理论分析是针对基波来衔接的，实际变频器输出波形中还有谐波分量。

为了解决这个问题，采用固定角度切换的方法。对于SVPWM，开关频率为600Hz，在参考矢量频率为45Hz时，在一个周期内参考矢量在360°空间内采样600/45=13.33次，其中必定有一次落入0～28°区间，仅当参考矢量落入这个区间内时才由SVPWM切换至SHEPWM。而从SHEPWM切换至SVPWM时，也仅当A相的相位落入某一固定角度区间时才切换至SVPWM。由于切换位置固定，其现象和行为是可重复的，在理论分析的基础上，通过实验对其进行微调，可以得到满意的结果。其实现流程如图3-35所示。

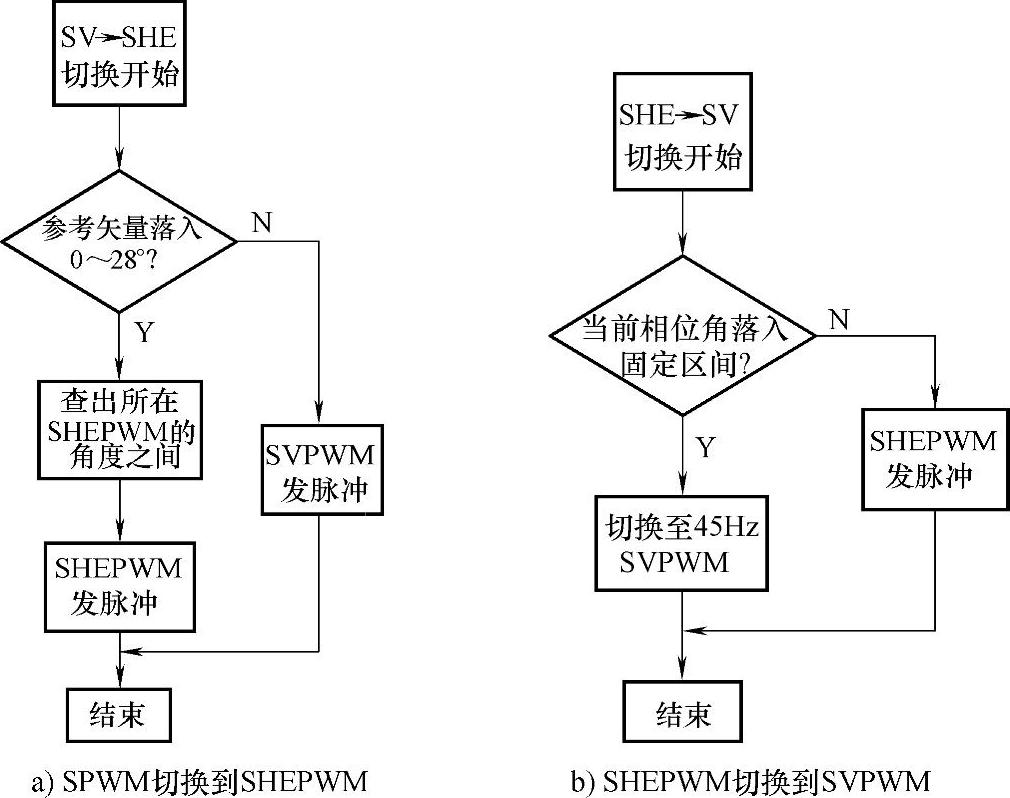
图3-35 SVPWM和SHEPWM切换流程图

（3）小电机实验结果

实验采用开关器件为IGBT，380V，3kW笼型异步电动机拖动一个他励直流电动机负载，控制系统采用自主研发的双DSP变频调速控制平台。图3-36所示为20Hz时SVPWM的逆变器输出波形及其频谱，图3-37所示为50Hz时SVPWM和SHEPWM的逆变器输出线电压及其频谱。图3-38所示为SVPWM和SHEPWM混合调制在45Hz切换时的逆变器输出波形。从电流波形上可以看出衔接过程基本上很平稳，没有出现相位的跳变。图3-39所示为经过LC滤波后的电机输出波形。可以明显看出，SHEPWM的电机线电压和电流脉动要远远小于SVPWM，而且切换过程比较平稳，验证了混合调制的正确性。

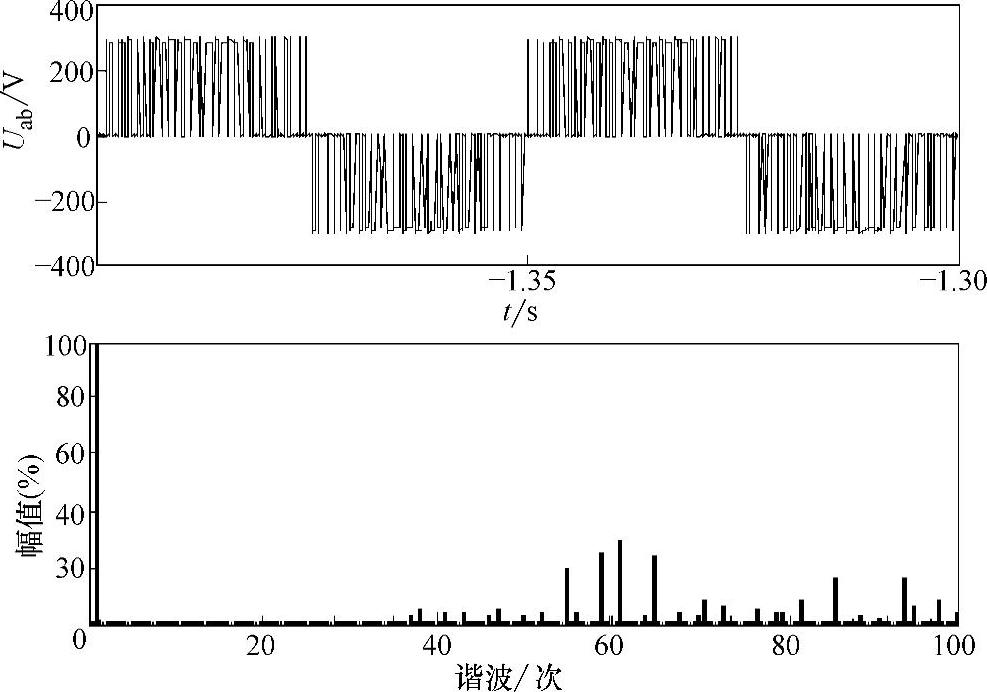
图3-36 三电平SVPWM实验波形（20Hz，m=0.4）

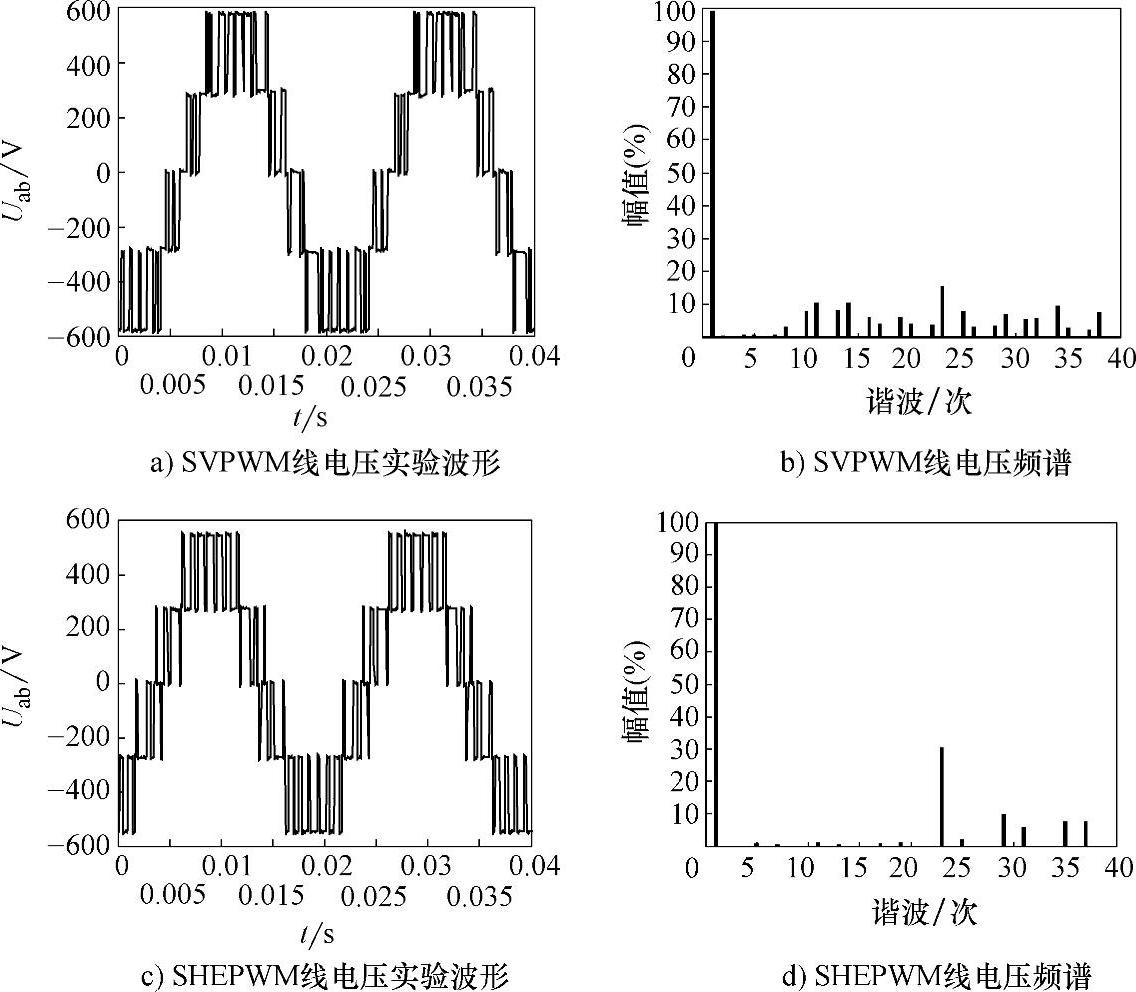
图3-37 三电平SVPWM和SHEPWM实验波形（50Hz，m=0.9）

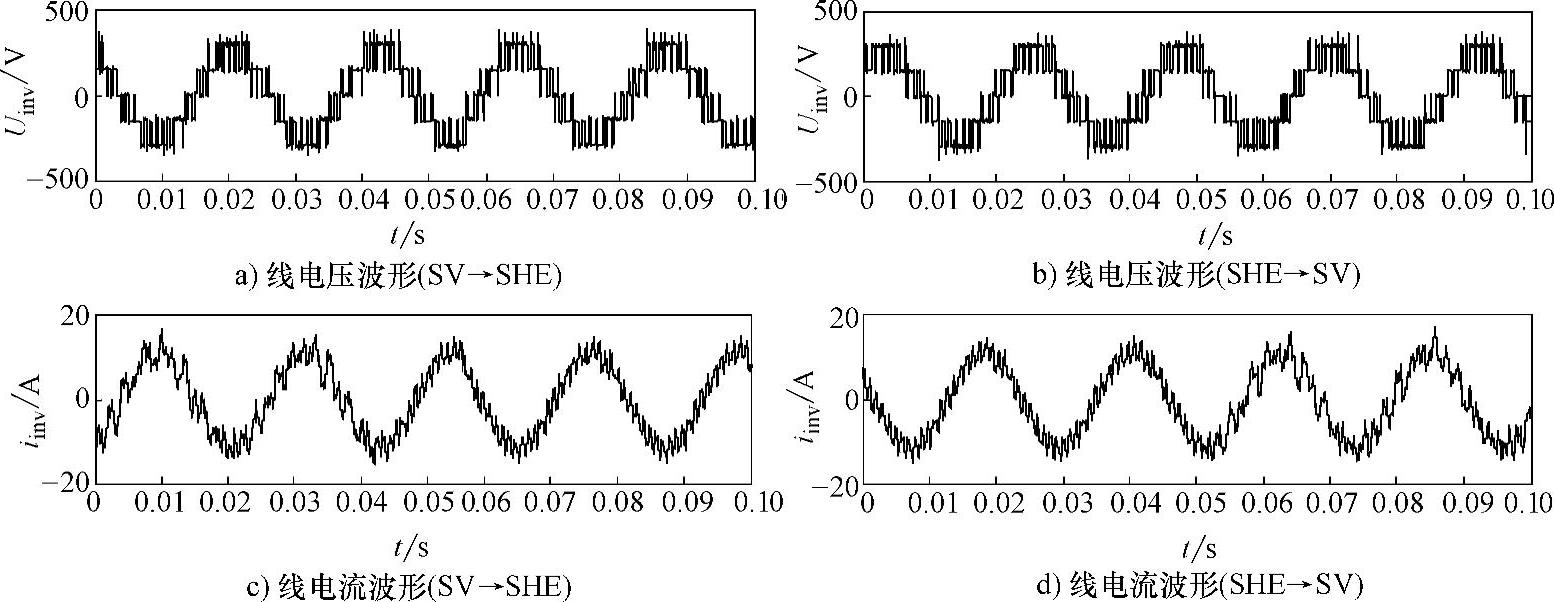
图3-38 SVPWM和SHEPWM在45Hz切换时的逆变器输出波形

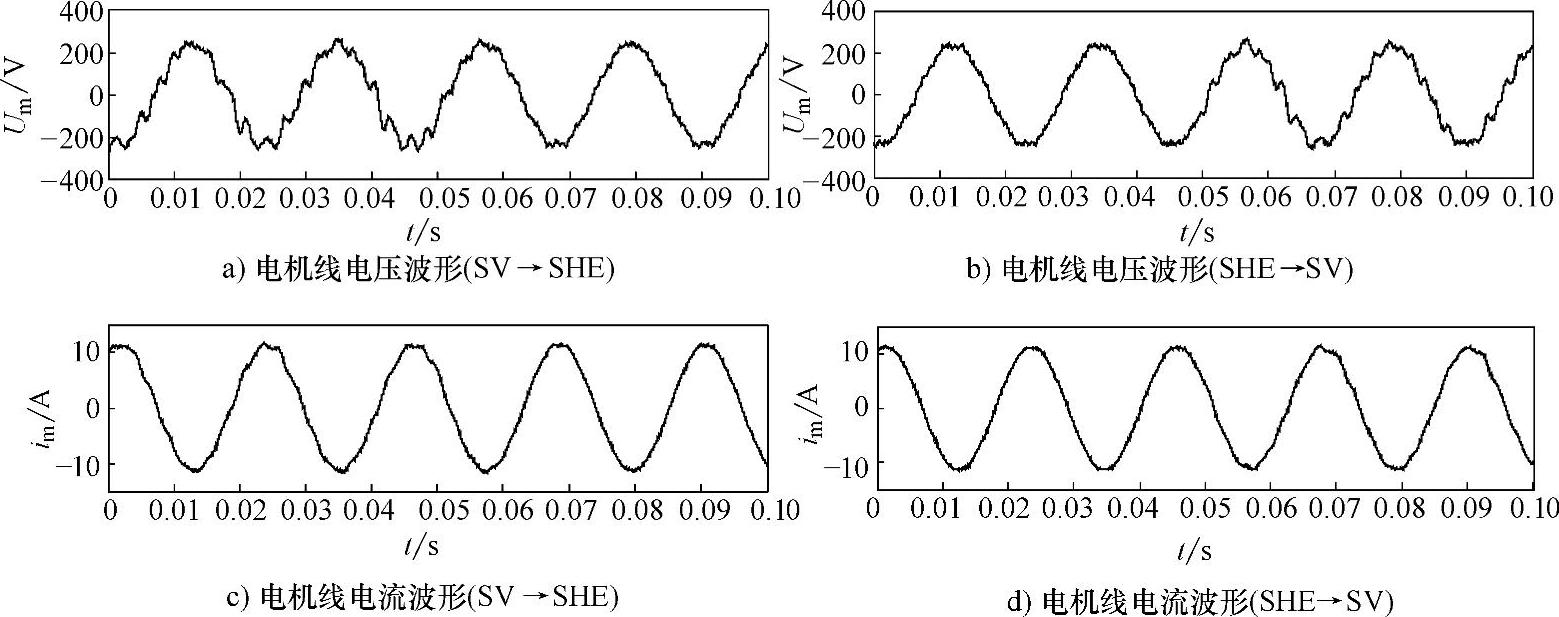
图3-39 SVPWM和SHEPWM在45Hz切换时的电机波形

（4）大电机实验结果

进一步在6kV/1250kW三相笼型异步电动机上进行实验，在45Hz下采用SVP-WM，在45Hz以上采用SHEPWM。图3-40所示是从SHEPWM切换到SVPWM时的逆变器输出线电压和线电流波形，图3-41所示是从SHEPWM切换到SVPWM时的电机线电压和电流波形，其中变频器输出电压采用高压探头直接测得，电机端电压采用电阻分压测得。可以看出，两种调制方法之间切换平滑，没有过电流和波形紊乱现象发生。SHEPWM的平均开关频率是45×7=315Hz，略高于SVPWM的开关频率300Hz，但是采用SHEPWM时电压波形更加规则，电流谐波大大减少。现场长时间运行表明，与相同开关频率的SVPWM相比，采用SHEPWM可以获得明显的效率提升。

4.三电平SHEPWM总结

1）针对1/4周期对称SHEPWM提出了不同于现有文献的三电平SHEPWM初值解经验公式，并验证了其收敛的快速性和准确性，从而扩大了三电平SHEP-WM解的范围，为实际中应用提供了更多的选择。研究并发现SHEPWM在高调制比时会存在多组解。以N=7为例给出了四组解轨迹，通过实验验证了其正确性。实验结果表明，四组解都达到了抑制低次谐波的效果，但剩余谐波含量有所不同。

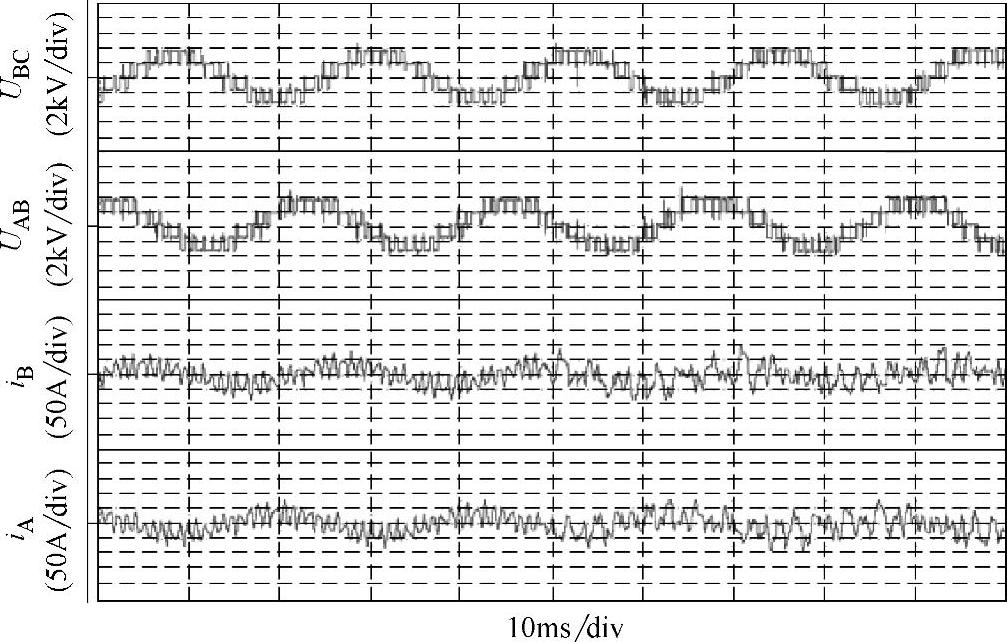
图3-40 SHEPWM切换到SVPWM时的变频器输出波形

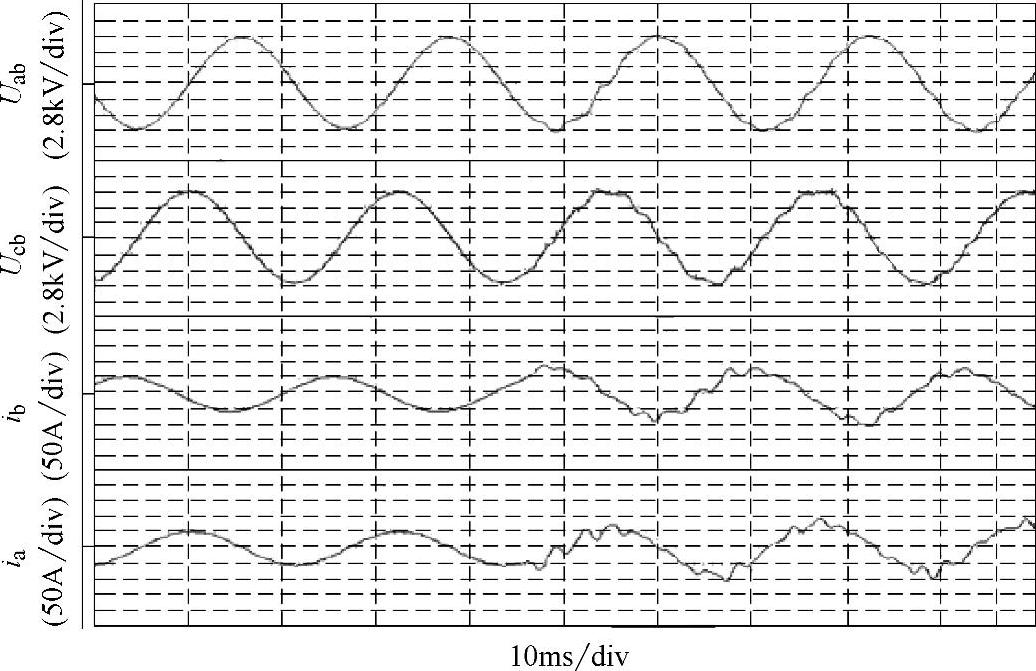
图3-41 SHEPWM切换到SVPWM时的电机输出波形

2）传统1/4周期对称SHEPWM中所有奇次谐波和基波的相位相同或相反，而1/2周期SHEPWM中谐波的相位可以是任意角度。在后者中考察SHEPWM，可以得到更多的解，并实际求解了开关点数N=7时1/2周期对称下的多组解。对1/2周期对称下SHEPWM的解进行了研究，根据其与1/4周期对称SHEPWM解的联系将其分成两类。与1/4周期对称SHEPWM的解相比，解类型Ⅰ主要是谐波相位发生变化，幅值变化不大，而解类型Ⅱ在所有谐波的相位和剩余谐波的幅值上都有显著差异。通过实验验证了这里给出解的正确性。实验结果表明，虽然不同的解都可以达到消谐的效果，但对剩余谐波的控制不同。

3）在比较常见的几种应用于三电平NPC逆变器的PWM调制方法的基础上，提出了一种SVPWM和SHEPWM混合调制方法。低频时采用异步SVPWM，由于载波比较高，可以较好地抑制低次谐波，减少谐波损耗和转矩脉动；高频时采用SHEPWM，进一步减少了输出电流脉动，降低了对滤波器的要求，而且由于存储量少，容易实现。文中还重点分析和解决了SVPWM和SHEPWM之间切换时的平滑过渡问题。采用PSIM软件对两种调制方法进行了仿真研究，并在实际三电平NPC变频器上进行了验证。仿真和实验结果证明，SVPWM和SHEPWM混合调制在整个工作范围内都可以有效地抑制低次谐波，尤其在高频时采用SHEPWM使谐波主要集中在高频部分，便于滤波器消除，大大减少了电流和转矩的脉动；二者之间切换平滑，具有较高的实用价值。