SVPWM最初是应用在电机调速领域中，其目标是控制电机的磁链为圆形。但实际上，在伏秒平衡的原理下，可以严格地推导出SVPWM的计算公式而无须考虑磁链。也就是说，它是一种通用PWM控制方法，可以应用于任何对象，而非专用于电机。目前，SVPWM作为一种PWM方式已经广泛应用于整流和逆变领域，其意义也不仅限于原来的控制磁链。图3-12a所示是三电平逆变器的空间矢量图。目前关于三电平SVPWM研究的主要内容有SVPWM算法及其实现^[34-35]、SVPWM和载波PWM的本质联系^[36-38]、过调制^[39-40]等。

在三电平NPC逆变器中存在大量冗余矢量，不同的矢量选择对应不同的PWM方案。本节介绍目前采用较多的一种方案，即把一个大扇区分成6个小扇区，矢量合成采用7段式输出，所有输出矢量的首发矢量采用正小矢量或负小矢量，这样保证了在不同扇区切换时线电压和相电压都没有跳变。

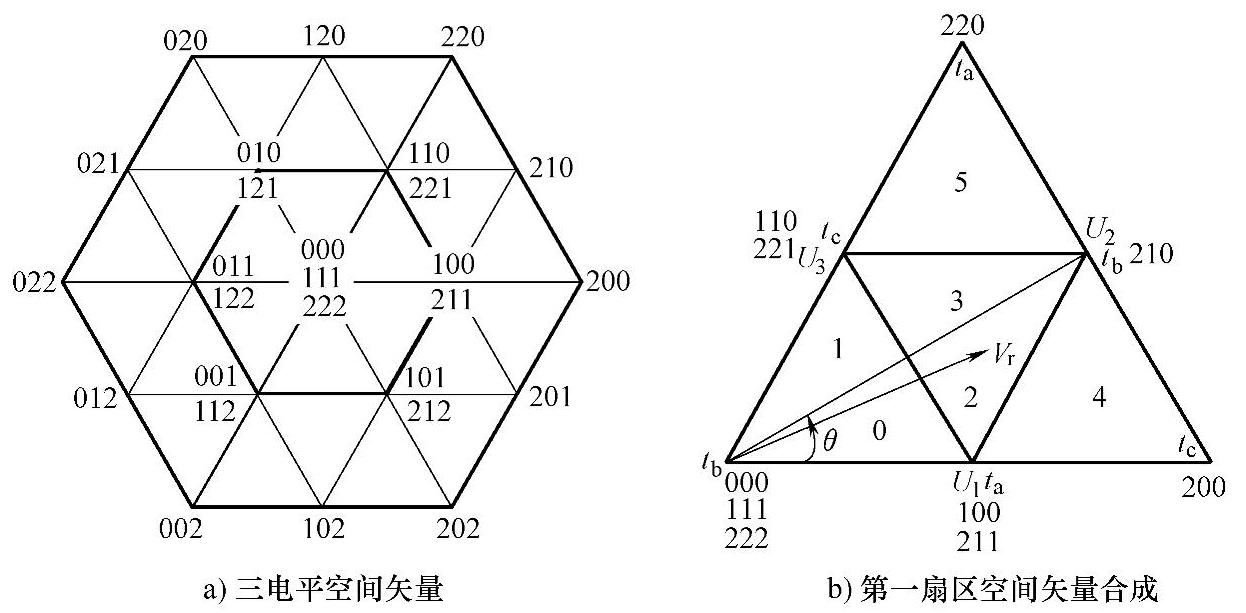
图3-12 三电平SVPWM原理

以大扇区一为例，进一步分成6个小扇区，图3-12b中参考矢量落入编号为2的小扇区中。由空间矢量合成原理，可得在一个开关周期T_s内有^[41]

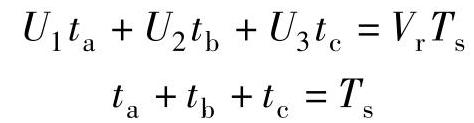
式中 ，，，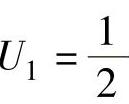

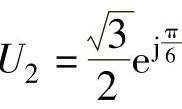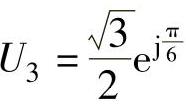求解可得

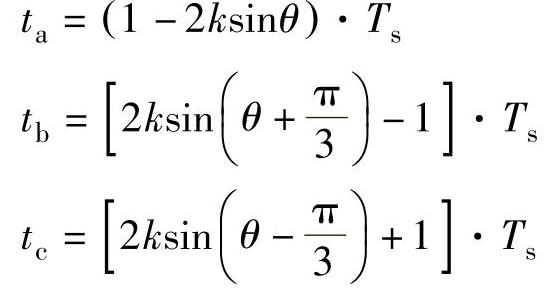
式中 ——调制比。

在小扇区2的矢量输出为211-210-110-100-110-210-211，类似的可以得出参考矢量落入其他扇区时各个矢量的合成时间及作用次序，见表3-1。

表3-1 三电平第一扇区的矢量输出顺序

三电平SVPWM在实际应用中有很多形式，如不对称的4段式、对称的5段式和7段式等。不同方法的开关次数和谐波特性也不一样，但一般来说，开关次数少时相应的谐波特性也要差一些，即谐波特性的提高是以开关频率为代价的。图3.13给出了采用5段式和7段式对称输出时线电压波形及频谱的对比，条件为调制比m=0.9，输出频率f=50Hz，开关频率=500Hz。可以看出采用5段式时低次谐波的含量要高于7段式。

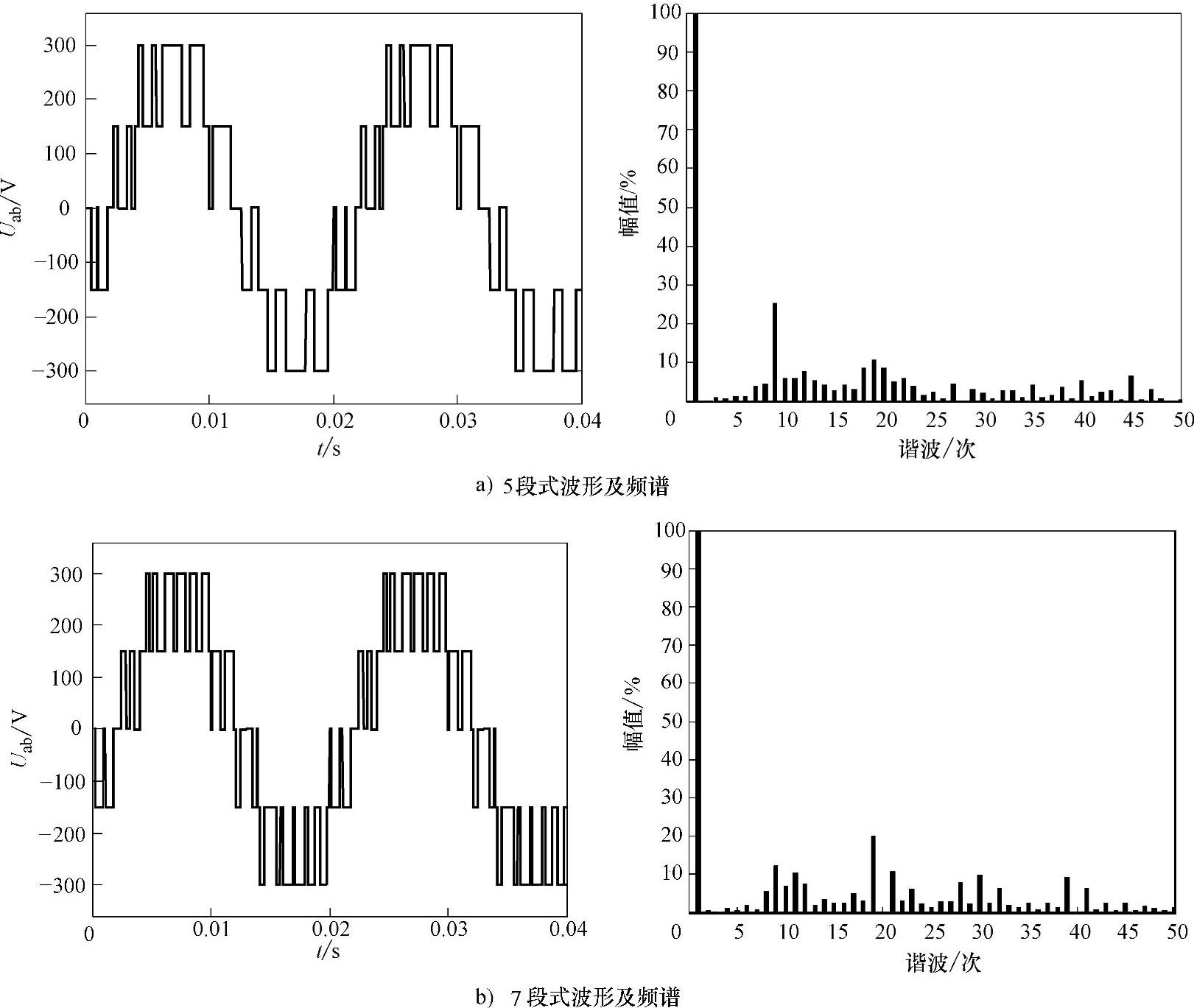
图3-13 5段式和7段式波形对比(www.daowen.com)

SVPWM的算法和SPWM相比比较复杂，尤其电平数增多时。不少文献对此进行了研究，提出了不少通用SVPWM算法。由于SVPWM空间矢量图是正六边形，在60°坐标系^[35，41]下考察SVPWM，可以大大简化SVPWM算法。此外，还有一些其他方法，如基于120°坐标系^[42]的算法、基于两电平的多电平SVPWM算法^[43]等，本质上基本一样。从参考文献[41]可知，在60°坐标系下参考矢量的坐标只与线电压有关系，从而揭示了空间矢量PWM本质上是基于线电压的PWM，不同的矢量方法在线电压上是一致的，但各相电压可能不一致，即零序分量不同。

SVPWM和载波PWM具有本质的联系，可以认为SVPWM是一种注入零序分量的载波PWM。这样尽管相电压发生了偏移，但在线电压中是相互抵消的。SVPWM的等效调制波在两电平已经有严格的推导和证明^[44-45]，在多电平中也从不同角度进行了解释^[46-47]。SVPWM和载波PWM等效的基础是伏秒平衡，即一个开关周期内电压对时间的积分相等。

对更多电平时的SVPWM难以求出其等效调制波的解析表达式，但很容易通过仿真得到其等效调制波的图形表示。以调制比m=0.9为例，图3-14给出了采用不同方法时三电平SVPWM的等效调制波。

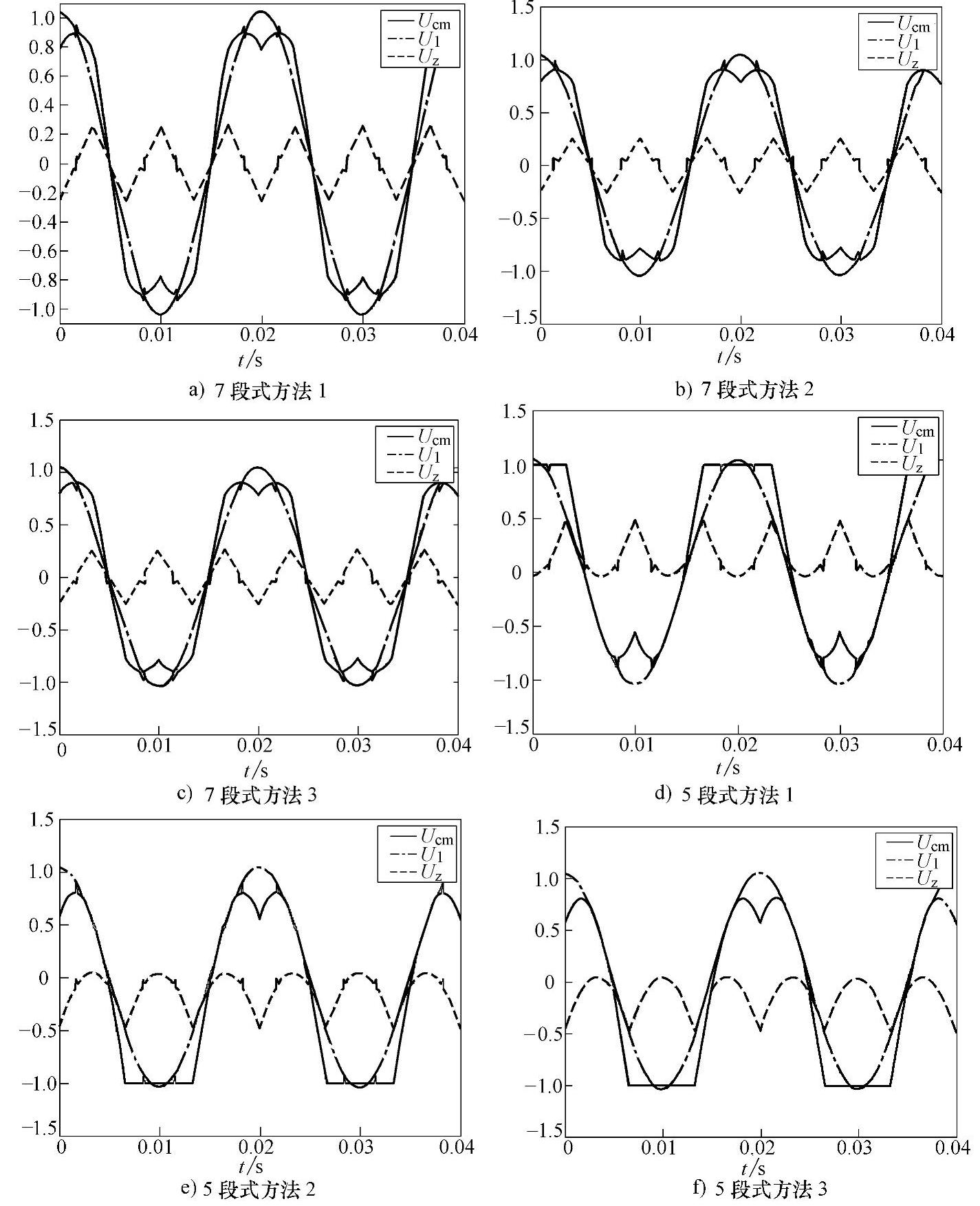
图3-14 三电平SVPWM的等效调制波

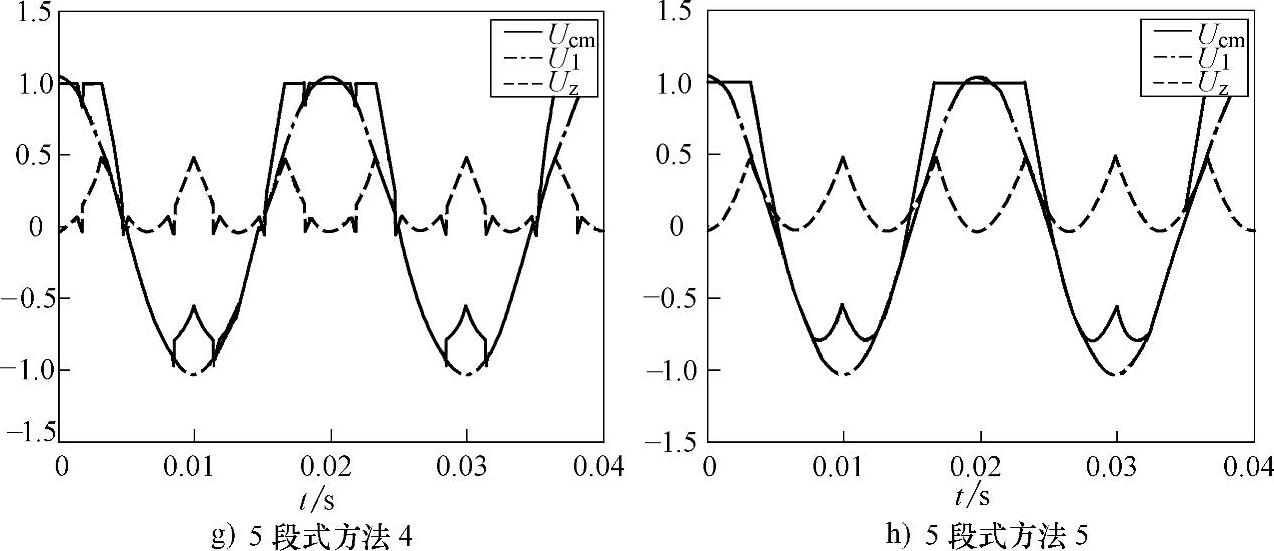
图3-14 三电平SVPWM的等效调制波（续）

过调制也是SVPWM研究的一个重要内容。在调制比大于1时，输出波形要从SVPWM切换到六脉波。如何平滑地切换，使基波电压仍然和直流母线电压呈线性关系并且减少谐波是需要研究的一个问题。不少文献^[48-49]研究了SVPWM的过调制策略，通常是分成两个阶段，计算比较繁杂，实现起来比较困难。因此，研究开发简单快速的过调制策略，对需要过调制的应用场合是很有意义的。

在三电平SVPWM中解决中点平衡、最小脉宽和死区补偿与三电平载波PWM中的方法并无本质区别，只不过是具体分析和实现的角度不同而已。在3.3.2节中已经对中点平衡方法进行了详细论述和对比，这里重点说一下最小脉宽。最小脉宽的影响在低频时尤为严重，这可以从逆变器输出波形的合成矢量看出来。图3-15所示为5Hz稳态时的逆变器输出波形综合矢量图。本来参考综合矢量是均匀分布的（如图3-15a所示），由于死区和最小脉宽的影响，使得最后实际发出的等效综合矢量的幅值和角度发生了偏移（如图3-15b所示），经计算最大偏移达28°。可以看出，最小脉宽的影响直接导致了输出电压波形的畸变^[50]。

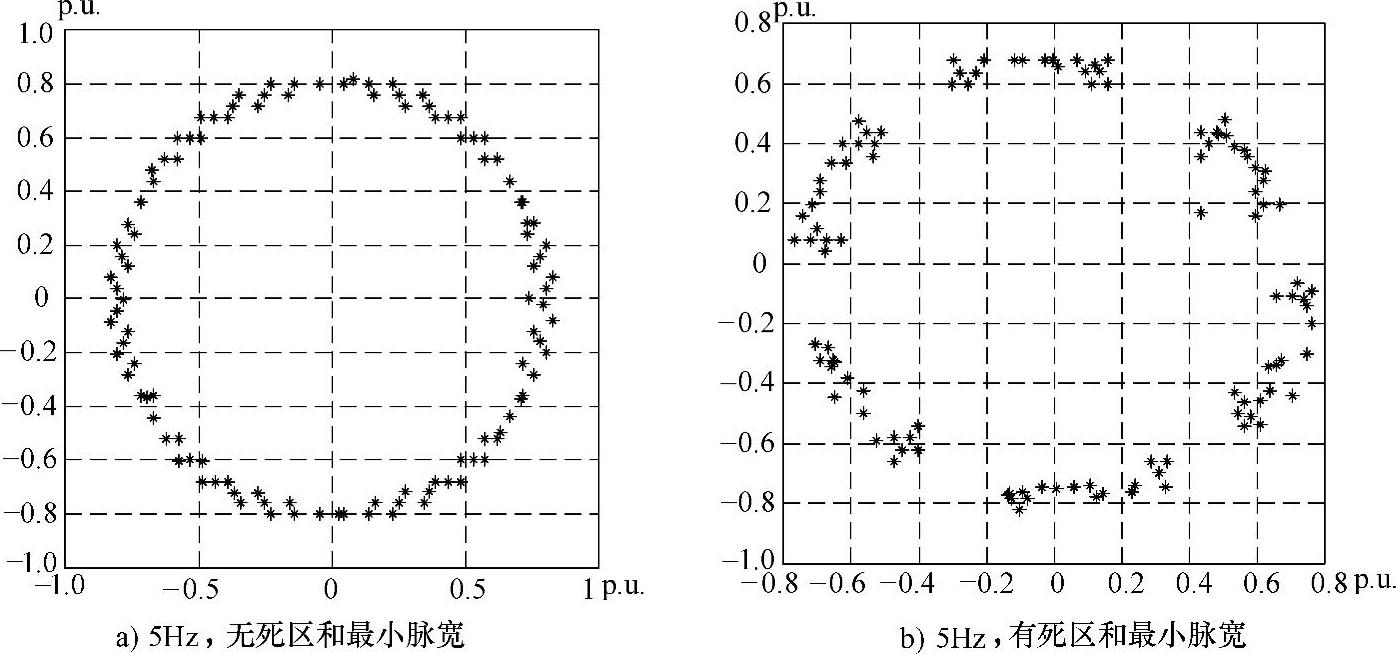
图3-15 有无死区和最小脉宽时输出波形的等效综合矢量对比

图3-16给出了第一大扇区内单个矢量作用时间小于最小脉宽的区域（阴影部分），其中h=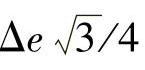（假设大扇区的边长为1），Δe的定义见3.3.2节。但落入阴影区域，并不一定意味着会出现单管的最小脉宽，还与矢量方法和顺序有关。通过适当分割作用时间长的矢量来重新组合矢量顺序，可以避免最小脉宽。参考文献[24]将一个大扇区内的区域划分成12个区域，在每个区域采用不同的矢量序列，但过于烦琐。考虑到实际应用，可以简单划为三部分。在调制比很小（m＜0.05，图3-16中第Ⅰ区域）时，首发零矢量；在大部分中间区域（0.05＜m＜0.95，图3-16中第Ⅱ区域）采用首发小矢量的方法；调制比很大（m＞0.95，图3-16中第Ⅲ区域）的情况在高压大容量里很少遇到，因为通常直流母线电压留有一定裕量，可以不予考虑。事实上，参考文献[24]就是把图3.16中的Ⅲ区域划分成了5块，造成了不必要的烦琐，在实际中不一定实用。

图3-17给出了三种矢量方法在调制比m=0.05时的相电压波形的对比，为了便于比较，输出频率f=50Hz，开关频率f_s=500Hz。其中，图3-17a采用传统首发小矢量的7段式方法，图3-17b采用首发零矢量的7段式，图3-17c采用输出全部矢量的方法。显然，图3-17a中存在很多窄脉冲，而图3-17b和图3-17c中的脉冲要宽很多，都远远大于器件的最小脉宽，所以在低调制比时采用后两种方法可以有效地避免最小脉宽。不过后两种方法也各有优缺点，图3-17b中采用的同一状态的小矢量，不容易考虑中点平衡，图3-17c的方法中含有所有矢量，容易考虑中点平衡，但是其开关频率采用7段式的两倍。

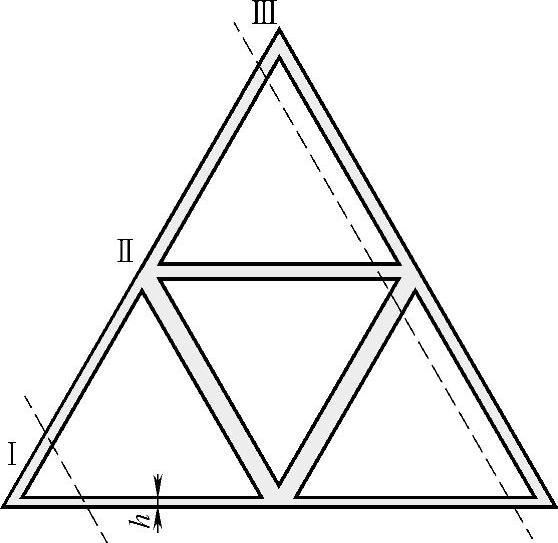
图3-16 三电平SVPWM的最小脉宽区域